Abstract
Bimodal atomic force microscopy uses a cantilever that is simultaneously driven at two of its eigenmodes (resonant modes). Parameters associated with both resonances can be measured and used to extract quantitative nanomechanical information about the sample surface. Driving the first eigenmode at a large amplitude and a higher eigenmode at a small amplitude simultaneously provides four independent observables that are sensitive to the tip–sample nanomechanical interaction parameters. To demonstrate this, a generalized theoretical framework for extracting nanomechanical sample properties from bimodal experiments is presented based on Hertzian contact mechanics. Three modes of operation for measuring cantilever parameters are considered: amplitude, phase, and frequency modulation. The experimental equivalence of all three modes is demonstrated on measurements of the second eigenmode parameters. The contact mechanics theory is then extended to power-law tip shape geometries, which is applied to analyze the experimental data and extract a shape and size of the tip interacting with a polystyrene surface.
Introduction
Over the decades since its invention [1] the atomic force microscope (AFM) has been used in a variety of modes to characterize micro- and nanoscale heterogeneous structures in composites and other advanced materials. The AFM can provide high resolution topographic and mechanical properties mapping using techniques such as force curves [2,3], contact resonance [4,5], force modulation [6,7], phase imaging [8,9], loss tangent imaging [10], friction force microscopy [11], creep compliance [12], shear modulation force microscopy [13], pulsed force microscopy [14] and torsional approaches [15]. These techniques can be broadly classified as either “parametric” or “spectroscopic” techniques.
In parametric nanomechanical techniques, the sample properties are deduced from changes in the parameters of a driven cantilever that is oscillating in a (quasi) steady state while interacting with the sample surface. For example, tapping-mode AFM [16,17] (also known as amplitude-modulation (AM) AFM [18-20]), is one of the most commonly used parametric techniques, where the cantilever is driven on resonance and the cantilever–sample distance is adjusted by a feedback loop to maintain a constant oscillation amplitude at every image pixel. The time required for the cantilever to reach a steady state defines the acquisition speed, allowing tapping-mode imaging to achieve very high speeds ultimately only limited by the cantilever bandwidth. However, the small number of tapping-mode observables (amplitude and phase) limits the extraction of absolute storage and loss moduli, as they cannot be distinguished from changes in indentation depth. In tapping mode, only the ratio of the storage to loss modulus can be measured [10,21,22]. The same limitation applies to many other parametric techniques, such as force modulation [6,7] and other single-frequency imaging modes, such as frequency-modulation (FM) AFM [23]. Separating the storage and loss moduli, and quantifying them, requires either additional independent observables or the use of spectroscopic methods.
Spectroscopic techniques rely on changing the operating conditions of the cantilever to provide the necessary information to extract nanomechanical properties of the sample for a given image pixel. This can be achieved by changing the cantilever–sample distance [24] or sweeping the drive frequency [25], amongst others [26]. Examples of well-established spectroscopic techniques are nanoindentation [27] and force curves as well as dynamic force curves performed with an oscillated cantilever. The time-varying cantilever response serves as input to a model for extracting nanomechanical properties of the sample at any location. These techniques are by nature slow for imaging, as they measure time-varying changes of the cantilever at every pixel.
Recently, parametric techniques have been extended by driving two or more cantilever resonances simultaneously in order to increase the number of observables, which is required to quantify the storage and loss moduli. Advances in this direction include bimodal [28-33], trimodal [34] or more generally multimodal/multifrequency [35] techniques, and have demonstrated quantitative mapping without compromising on the high speeds that define parametric imaging techniques. Currently, state-of-the-art bimodal methodologies are mostly based on FM-AFM techniques that rely on elaborate mathematical theories [36-41], involving fractional calculus and Laplace transforms for relating AFM observables to nanomechanical properties. The mathematical complexity of these techniques can obscure physically intuitive understanding of the cantilever dynamics in bimodal AFM experiments.
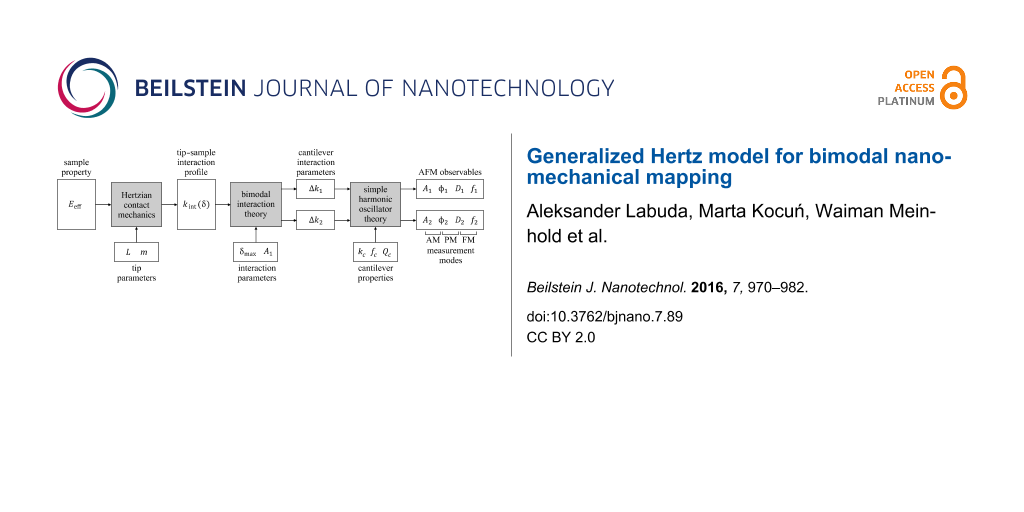
Here, we present a simplified theory for bimodal AFM with a large fundamental resonance oscillation amplitude and small higher resonance amplitude. The theory is based on a binomial approximation of the weight function for extracting the interaction stiffness for both resonant modes, each yielding a simple analytical expression. These two independent pieces of information are refactored to provide information about modulus and indentation depth. While the theory is generally applicable to a wide range of tip–sample interaction models, the derivation here begins in the context of a Hertzian contact with a paraboloidal tip and is then generalized to any tip shape described by a power-law profile. This theory is then experimentally applied to three variations of bimodal AFM involving different dynamic AFM modes of operation [42,43], namely amplitude modulation (AM) [1,18,19], phase modulation (PM) [43-46] and frequency modulation (FM) [23,36,47]. Finally, a method for extracting the tip size and tip shape from bimodal AFM approach curves is presented and demonstrated on a polystyrene sample. Figure 1 provides a diagram of the theory presented in the following three sections.
Figure 1: Diagram of the theory presented in this paper, showing relationship between inherent sample properties and tip geometry parameters to the AFM observables for bimodal AFM in the context of Hertzian contact mechanics. The tip shape is assumed to have a power-law profile with size parameter L and shape parameter m.
Figure 1: Diagram of the theory presented in this paper, showing relationship between inherent sample propert...
Methods
Hertzian contact mechanics
The Hertzian contact model involves the interaction stiffness kint versus indentation depth δ between a paraboloidal tip of radius R and a flat sample as
where the effective Young’s modulus Eeff combines deformation of the tip and sample [48]. Similar expressions can be derived for a tip in the shape of a punch or a cone [49].
Here, these three special cases are generalized to any axisymmetric tip shape whose cross-sectional radius r, as a function of height z, is governed by the power law
where the characteristic length scale L and the exponent parameter fully define the tip size and shape, respectively. Figure 2a illustrates Equation 2 for five values of m, including the three special cases of punch, paraboloid, and cone. Note that “sphere” is used as a shorthand for “paraboloid” in the scientific vernacular.
Figure 2: a) The generalized tip shape is drawn for various values of m. b) The indentation of a paraboloidal indenter into an elastic surface illustrates the distinction between the cross-sectional indentation radius versus the true contact radius.
Figure 2: a) The generalized tip shape is drawn for various values of m. b) The indentation of a paraboloidal...
Upon purely elastic indentation of such a power-law indenter into a sample surface to an indentation depth δ, the true contact radius rc is smaller than the cross-sectional radius r(δ) because of deformation of the surface, as can be understood from Figure 2b. The exception is the punch model for m = 1, where no reduction in radius occurs. The contact radius correction factor αc quantifies the reduction in contact radius rc with respect to r(δ) by
As expected, αc = 1 for m = 1 (punch), and then αc monotonically decreases to αc = 2/π ≈ 0.64 for m = 2 (cone). The mathematical form of αc is presented in the Appendix (b).
Importantly, it is the true contact radius rc that defines the tip–sample interaction stiffness, as derived by Oliver and Pharr [27]:
Substituting in the expression for rc leads to the general form
The interaction stiffness in Equation 5 is plotted for three special cases in Figure 3. For the punch model with m = 1, the length scale parameter L is equal to the punch radius R. For the paraboloidal indenter model with m = 3/2, L is the effective “sphere” diameter 2R. For the conical indenter with m = 2, L drops out and the cone half-angle θ = 45°. (Given the loss of the length scale parameter L in the degenerate case m = 2 (cone), a half-angle parameter θ may be introduced by multiplying kint by (tan θ)−1 to fully define the geometry of the conical indenter, if necessary.)
Figure 3:
a) The cantilever motion during oscillation in bimodal imaging with only a small portion interacting with the sample. Note that the oscillation of the second eigenmode cannot be seen, as it is assumed infinitely small by the model proposed here. The stiffness profile of the interacting tip is plotted for three tip shapes: b) punch, c) paraboloid, d) cone. The weight functions used for integrating these stiffness profiles are shown for e) the first eigenmode (assuming a large amplitude) and f) the second eigenmode (assuming a small amplitude). The weight function for the second eigenmode diverges where the interaction stiffness is nonzero, reflecting the sensitivity of bimodal AFM to nanomechanical properties. The binomial approximation is illustrated for both weight functions; they are very accurate approximations in the interaction range, and can be used to derive a simple analytical solution for bimodal imaging. Note: the three different x-axes shown in these plots are interchangeable; they reflect the most appropriate parameterization of the tip position in each case.
Figure 3: a) The cantilever motion during oscillation in bimodal imaging with only a small portion interactin...
Bimodal interaction theory
This section first describes how the tip–sample interaction stiffness of a paraboloidal (“spherical”) tip affects the changes in effective stiffness of the first and second eigenmodes of the cantilever. Then, the results are generalized to a power-law tip shape.
Paraboloidal tip
For the first eigenmode driven with a large oscillation amplitude A1, the change in stiffness of the interacting cantilever Δk1 averaged over one cycle can be computed by integrating kint(δ) with a semi-circular weight function that spans the peak-to-peak cantilever oscillation [50], as represented in Figure 3. Mathematically,
where δmax is the maximum indentation depth and the normalized distance u = (δmax − δ)/A1. It is worth noting the distinction between kint(δ), which is the instantaneous stiffness profile experienced by the oscillating cantilever tip, and Δk1, which is the time-averaged effective change in stiffness of the cantilever–tip–sample system that is experimentally measurable by the AFM user. Measuring Δk1 is the topic of Section ‘Simple harmonic oscillator theory‘, presented later.
In the limit that the fundamental amplitude A1 is much larger than the interaction length scale, the stiffness profile kint(δ) only affects a small portion of the cantilever sinusoidal oscillation where the tip indents the sample, as shown in Figure 3a. Therefore, the integration limits in Equation 6 reduce to [0, δmax/A1] such that u << 1 throughout the integration. Consequently, the weight function can be approximated very accurately with the first term in the binomial expansion, This approximation, used previously [51], is graphically illustrated in Figure 3e,f. Applying it to Equation 6 results in
which can be easily integrated for a paraboloidal indenter to give
The relative error in Δk1 introduced by the binomial approximation is quantified in Figure 4; it typically falls on the order of 1% in large-amplitude dynamic AFM, where the interaction amplitude A1 greatly exceeds δmax.
Figure 4:
The relative error introduced in the calculation of Δk1 because of the approximation applied to Equation 6 in the case of a punch, paraboloid, and cone contact model. The
approximation applied to Equation 10 results in a similar, albeit negative, error.
Figure 4:
The relative error introduced in the calculation of Δk1 because of the approximation applied to Equation 6 i...
Meanwhile, the second (or higher) eigenmode is deliberately driven at a small amplitude A2, such that the interaction stiffness it experiences is roughly constant throughout one of the higher eigenmode oscillation cycles. However, the instantaneous interaction stiffness experienced by the second eigenmode slowly changes along the trajectory of the first eigenmode. Because the second mode rides along the slower sinusoidal motion of the first mode, its time-averaged change in interaction stiffness Δk2 can be calculated by
where T is the oscillation period of the first eigenmode. A rigorous derivation of Equation 9 is provided in Appendix (a). Parametrizing this time integral with respect to distance by the substitution t = cos−1(u)/ω1 results in
Similarly to the approach taken with the first eigenmode, this integral can be solved analytically for a paraboloidal indenter after applying the binomial approximation such that
Note that the second-mode change in stiffness scales linearly with indentation depth, Δk2δmax, while the first mode stiffness scales with the square of the indentation depth,
. These scaling laws have been verified experimentally for a paraboloidal indenter [39]. The system of two equations (Equation 8 and Equation 11) can be solved for two unknowns, namely
and
This operation is central to bimodal imaging, as it separates the changes in modulus from changes in indentation depth. This distinction cannot be made in single-mode dynamic AFM imaging.
The key to bimodal nanomechanical imaging is that the same stiffness profile is measured simultaneously by two different eigenmodes with different weight functions: and
The fact that these weight functions are related by a derivative operation results in independent measures of nanomechanical properties by both eigenmodes while imaging. Notably, the fact that the weight function of the second eigenmode increases drastically as the tip approaches the sample, as seen in Figure 3f, explains the high sensitivity and increased spatial resolution of bimodal imaging noted in the past [52].
Power-law tip
The derivation so far revolved about a paraboloidal indenter. Applying the same approach used in Equations 6–13 to the generalized stiffness profile of Equation 5 result in the generalized indentation and modulus equations
and
where β is a scaling constant that depends only on m and is mathematically defined in the Appendix (c). As expected, choosing m = 3/2 in Equation 14 and Equation 15 recovers Eqution 12 and Equation 13.
The tip shape exponent m is a free parameter in the generalized stiffness profile. It can be inferred experimentally by measuring changes in Δk1 and Δk2 for a fixed A1 and relating them to Equation 15 by the scaling law
as will be demonstrated later.
Simple harmonic oscillator theory
Measurements of Δk1 and Δk2 are necessary for calculating δmax and Eeff in Equation 12 and Equation 13 or Equation 14 and Equation 15.
A single equation that extracts Δk from a driven eigenmode (on and off resonance) with any number of changing AFM observables is presented in the Appendix (d). The derivation assumes the eigenmode in question can be modeled as a simple harmonic oscillator (SHO) within the range of interactions explored in the experiment. Here, three special cases (AM, PM, FM) for starting an experiment on-resonance were extracted from the general SHO solution for simplicity. These special cases are presented in Table 1, and described in the following subsections. The constant-excitation FM mode (CEFM) is also included in Table 1 for completeness.
Table 1: Using an automatic-gain-controller (AGC) and/or phase-locked-loop (PLL) to control the cantilever amplitude and frequency, respectively, leads to four combinations of measurement modes: amplitude modulation (AM), phase modulation (PM), frequency modulation (FM), and constant-excitation frequency modulation (CEFM). Using these modes for measuring Δk1 and Δk2 of a cantilever independently leads to 16 bimodal configurations: AM-AM, AM-PM, AM-FM, FM-FM, etc.
| Phase-locked-loop (PLL) | |||
|---|---|---|---|
| OFF | ON | ||
| Automatic-Gain-Controller (AGC) | OFF | AM mode | CEFM mode |
| ON | PM mode | FM mode | |
The last subsection extends the SHO theory to measuring two eigenmodes simultaneously, as required for bimodal AFM.
Amplitude modulation (AM) mode
For an eigenmode driven in AM mode, the corresponding time-averaged interaction stiffness can be calculated from the measured interaction amplitude A and interaction phase as in
while the cantilever quality factor Qc, the cantilever stiffness kc, and the reference amplitude Ar are all measured in the absence of tip–sample interactions (Ar is often referred to as the “free amplitude”).
Phase modulation (PM) mode
Alternatively, PM mode uses an automatic-gain-controller (AGC) to maintain a constant cantilever amplitude A by varying the drive amplitude D; meanwhile, the drive frequency remains fixed just as in AM mode. In this mode,
Note that an AGC is especially beneficial for use on the second eigenmode, because A2 is often chosen close to the detection limit and may drop substantially in AM mode when the resonance frequency shifts upon interaction with the sample. The AGC in the PM mode assures that A2 remains above the detection limit throughout the experiment.
Frequency modulation (FM) mode
If FM mode is employed for any of the eigenmodes, where the resonance frequency fc is tracked with a phase-locked-loop (PLL), the measured frequency shift Δf can be used to estimate the interaction stiffness by the approximation
In this mode, the oscillation amplitude is held constant with an AGC. The use of an AGC will be assumed for “FM mode” henceforth.
Alternatively, constant-excitation FM mode (CEFM) employs a PLL but does not use an AGC [53,54]; therefore, the oscillation amplitude is not necessarily constant throughout the tip–sample interaction. This less-common technique is not explored in this article.
Bimodal configurations
In bimodal AFM, both eigenmodes behave like independent SHO’s because the first mode is driven in the large-amplitude limit and the second is driven in the small-amplitude limit. An empirical verification of this independence will be performed and discussed later.
In principle, both Δk1 and Δk2 can be measured with any of the four measurement modes described so far, leading to 16 possible configurations: AM-AM, AM-PM, AM-FM, FM-FM, etc. As an example, the first experimental bimodal measurements were taken in the AM-AM configuration [33]. In their pioneering work, Heruzzo and Garcia demonstrated FM-FM measurements [39,55]. Here, the AM-AM, AM-PM and AM-FM configurations are explored in detail. Practical considerations for these choices will be discussed later.
Results
A polystyrene surface was probed with bimodal approach curves (also known as “force–distance” curves), where the bimodally oscillating cantilever approaches the sample with a constant velocity. The experiment is described in the first subsection, where the AM-AM, AM-PM, and AM-FM configurations are compared to investigate the validity of the SHO model assumed by the bimodal theory. Then, multiple approach curves are used to extract the shape and size of the tip. Finally, the newly defined tip geometry is used to extract the modulus from all the approach curves to assess consistency of the results and their dependence on imaging parameters.
Experiment
The experiment was performed on a Cypher AFM with an ASYELEC-02 cantilever, which has a Ti/Ir-coated tip of nominal tip radius R = 28 ± 10 nm. Photothermal excitation [56] was used, which ensures stable imaging [57] and accurate FM tracking [58-60]. An automated calibration method [61] was used to obtain the stiffness of the first eigenmode (kc1 = 43.2 N/m), which was then used as a basis of calibration for the second eigenmode stiffness kc2 = 818 N/m by a recently established calibration protocol [62]. Next, a thermal power spectral density [63] of the cantilever was acquired close to the surface (within a few hundred nanometers) to determine the remaining cantilever properties (fc1, fc2, Qc1, Qc2). For this calibration step, the proximity to the surface is important. Performing it far from the surface incorrectly introduces long-range cantilever–sample interactions into the final measurement. Finally, the equipartition theorem was used to convert the amplitudes of both eigenmodes into nanometers [64-66].
Figure 5 shows approach curves acquired in the AM-AM, AM-PM, and AM-FM configurations. Equations 17–19 were used to recover values of Δk1 and Δk2 where appropriate. The excellent agreement between all three bimodal configurations across the entire approach curve suggests that the simple harmonic oscillator is a valid model to describe the second eigenmode of the cantilever in this experiment.
Figure 5: Experimental results from three consecutive approach curves on polystyrene using AM-AM, AM-PM, AM-FM configurations for the first mode (left) and second mode (right). The changes in effective cantilever stiffness for both modes (below) calculated from the observables of each mode (above) by using Equations 17–19, respectively (reference amplitude Ar1 = 60 nm).
Figure 5: Experimental results from three consecutive approach curves on polystyrene using AM-AM, AM-PM, AM-F...
Calibration of the tip shape and size
When driving the first eigenmode in the AM mode, large variations in indentation depth can be achieved by varying the reference amplitude Ar1 ("free amplitude") while keeping A1 fixed. Varying the reference amplitude is more effective than changing A1 which carries a weak dependence on indentation for a setpoint around A1/Ar1 ≈ 0.5. Consecutive bimodal approach curves on a polystyrene sample were performed while varying the reference amplitude Ar1 between 50 nm and 91 nm in 21 increments. The AM-AM, AM-PM, and AM-FM configurations were alternated. A total of 63 approach curves were performed within 45 min.
The values of Δk1 and Δk2 at a fixed amplitude (A1 = 40 nm) were used to determine the tip shape using the scaling law in Equation 16. The results are shown in Figure 6, where the exponent m values for each bimodal configuration were extracted from a power-law fit and shown to be equal within error; they averaged to m = 1.24 ± 0.04. This measurement of the tip shape (m) can now be used to calculate the tip size (L), which is uniquely determined if the sample modulus is known. Fitting Equation 15 to the data and setting Eeff = 3 GPa (as approximately expected for polystyrene [67]) results in a value for the tip length scale L = 32 nm. This tip characterization suggests a tip shaped as a rounded punch, somewhere between a punch of radius R = 32 nm and a paraboloid of radius R = 16 nm.
Figure 6: The set of approach curves in Figure 5 was repeated 21 times at various drive amplitudes. The values of Δk1 and Δk2 extracted at A1 = 40 nm from all 63 approach curves are plotted on a log–log scale. The line represents a power-law fit to the entire data, which can be used to determine the tip shape (m = 1.24) by Equation 16 and the tip size (L = 32 nm) by Equation 15. The inset shows the range of indentation depths probed in this experiment.
Figure 6: The set of approach curves in Figure 5 was repeated 21 times at various drive amplitudes. The values of Δk1...
With a defined exponent m value, the absolute indentation depth at the various Ar1 can be calculated by Equation 15, as shown in the inset of Figure 6. The calibration of the tip shape and size is expected to be valid for the explored range of indentations (between 0.6 nm and 1.2 nm in this case).
Measurement of modulus
With a modeled tip shape and size (m = 1.24, L = 32 nm), the modulus Eeff was extracted from all 63 approach curves, as shown in Figure 7. At A1 = 40 nm, the average modulus must be 3 GPa because this was the assumed value from which the tip size was extracted. Notably, the modulus appears to be independent of both A1 and bimodal configuration, as will be discussed in the next section.
Figure 7: a) The modulus Eeff for all 63 approach curves from Figure 6 was extracted as a function of oscillation amplitude A1. Not only is Eeff independent of interaction amplitude A1 and reference amplitude Ar1 (free amplitude), the three configurations (AM-AM, AM-PM, AM-FM) yield the same results within error. Note that a value of Eeff was only extracted for values A1/Ar1 < 0.75 to ensure that repulsive interactions dominate.
Figure 7: a) The modulus Eeff for all 63 approach curves from Figure 6 was extracted as a function of oscillation amp...
Discussion
Independence of imaging parameters
The approach curves in Figure 7 span indentation depths from 0.6 nm to 1.2 nm, interaction amplitudes from 25 nm to 70 nm, and reference amplitudes between 50 nm and 91 nm. The modulus values at A1 = 40 nm are constrained to match 3 GPa by the tip shape and size calibration. However, throughout this range of imaging parameters, the modulus also remains within a 0.15 GPa standard deviation (5%) of 3 GPa, with no obvious trend. In addition, the three bimodal configurations agree to better than this standard deviation.
The independence on imaging parameters provides confidence that the system was accurately modeled by a rounded punch of shape m = 1.24 and size L = 32 nm. In contrast, assuming a paraboloidal tip (m = 1.5) results in increased variability in the modulus, as well as noticeable dependence on imaging parameters. Also, assuming a paraboloidal tip results in a tip radius R = 93 nm for these experiments, which is far from the nominal radius for this cantilever tip (R = 28 ± 10 nm).
These results lead to the conclusion that calibrating the tip shape and size provided a more accurate picture of the tip–sample contact mechanics, which led in turn to improved accuracy in extracting the modulus of polystyrene over a wider range of imaging parameters.
Given that the bimodal AFM theory was derived in the context of Hertzian contact mechanics where only repulsive interactions are considered, only data where A1/Ar1 < 0.75 were analyzed to ensure that repulsive forces dominate over attractive and adhesive forces. This criterion is somewhat arbitrary and specific to the current dataset; other samples and tip geometries may require different threshold values of A1/Ar1 or may require more elaborate models.
AM/PM/FM equivalence
The agreement between AM, PM and FM modes of operation for Δk2 shown in Figure 5 validates the mathematical framework leading up to Equations 17–19 that assumes SHO behavior of the cantilever. This agreement is reassuring, as a sinusoidally-driven SHO model was used for both eigenmodes to derive the bimodal interaction theory that relates the cantilever parameters to the interaction profile. Furthermore, the agreement between the modes of operation suggests that the feedback loops used for the PM and FM modes tracked changes in the cantilever eigenmode appropriately.
Large and small amplitude approximations
The amplitude of the first mode was modeled in the large limit, while the amplitude of the second mode was modeled in the small limit. The validity of these assumptions was implicitly verified in the dataset acquired for this experiment, as described herein.
The analysis in Figure 7 suggests that the variations in interaction amplitude (25 nm < A1 < 70 nm) do not affect the outcome of the measured Eeff. This suggests that the large-amplitude limit for the first mode was fulfilled across the range of explored amplitudes.
The small-amplitude limit for A2 is tested by the comparison of experimental configurations. Whereas the second mode amplitude A2 for AM-AM drops significantly (from 500 pm to 200 pm) during a single approach curve, A2 for AM-PM and AM-FM is held fixed by the AGC. The fact that all three configurations lead to the same extracted Eeff suggests that the small-amplitude limit for the second mode was fulfilled.
Sensitivity of bimodal AFM
The high sensitivity of bimodal AFM was predicted in the theory described in Section ‘Bimodal interaction theory’ and attributed to the introduction of an additional eigenmode driven at a small amplitude. The argument was based on the fact that the weight function of the second eigenmode rises quickly as the tip approach the sample, as shown in Figure 3f.
This fact is demonstrated experimentally in the data of Figure 5, where Δk2 is 20× to 50× larger than Δk1. Whereas both Δk1 and Δk2 are weighted integrals of the identical stiffness profile kint(δ), the weight function of the second mode captures much more of the interaction stiffness for small indentations.
This illustrates the benefit of introducing a small-amplitude second eigenmode into the measurement: it provides a high-sensitivity channel of information, without disrupting the measurement as explained in the previous section.
Error from binomial approximation
The error introduced by the approximation that allowed the analytical closed-form in Equation 14 and Equation 15 is now calculated. In the worst case scenario for this experiment with δmax = 1.2 nm and A1 = 40 nm, a relative error of 0.5% is caused by the approximation
In turn, this results in an overestimation of 0.9% in indentation depth, and an underestimation of 1.0% in modulus as far as Equation 14 and Equation 15 are concerned. These errors from approximation are negligible compared with experimental variability and absolute calibration error.
Importantly, applying Equation 19 to both eigenmodes results in FM-FM equations that are identical to those derived by Herruzo et al. [38,39]. This leads to the conclusion that the approximation is sufficient for deriving analytical equations for bimodal FM-FM and other bimodal configurations. In other words, the use of fractional calculus, Laplace transforms, Padé approximants, and Bessel functions can be avoided with no loss in accuracy when deriving bimodal AFM theory.
Merits of AM-FM
Although the three configurations of bimodal methods tested in Figure 5 were equally accurate, the AM-AM method has the disadvantage of potentially having more noise relative to AM-PM, which in turn may have more noise relative to AM-FM. In AM-AM and AM-PM, the second eigenmode drive frequency is held fixed. In that case, when the second eigenmode resonance frequency shifts by more than its bandwidth (fc/2Qc), the signal-to-noise ratio degrades because the signal drops relative to the noise floor. Furthermore, in AM-AM operation, A2 decreases upon interaction with the surface – further aggravating the drop in signal-to-noise ratio. It is therefore often advisable to operate the second eigenmode in FM mode in practical situations.
On the other hand, the first eigenmode typically undergoes more modest changes in resonance frequency upon interaction with the surface. Also, these changes are controllable by the AFM user by the setting of an amplitude setpoint. For this reason, AM operation on the first eigenmode does not cause the same decrease in signal-to-noise ratio often observed on the second eigenmode. More importantly, dynamic AFM imaging in ambient conditions has relied on the robustness of AM (tapping-mode) imaging, mostly attributable to the monotonicity of the amplitude versus distance relationship, for stable operation and topography tracking.
For these two reasons, the authors generally recommend the use of AM-FM over the other configurations (AM-PM, FM-FM, etc.), as it is the most robust, versatile and sensitive configuration for bimodal nanomechanical mapping in a wide range of imaging conditions.
Conclusion
An analysis framework for bimodal AFM with a power-law tip and Hertzian contact was presented. The derived theory was used to extract the tip shape and size for an experiment on a polystyrene sample. For a wide range of imaging parameters, the experimental data returned a nearly constant modulus of the material when analyzed with this model. Three configurations (AM-AM, AM-PM, AM-FM) were tested and shown to provide equally accurate results, thereby supporting our assumption that the cantilever second eigenmode can be modeled as a simple harmonic oscillator for the range of interactions explored in the experiment.
The approximations used for deriving an analytical closed-form solution for bimodal AFM were also investigated. Both the first mode large-amplitude approximation and the second mode small-amplitude approximation were verified to be accurate for typical imaging conditions. Notably, the fact that the weight function of the second eigenmode increases drastically as the tip approaches the sample explains the high sensitivity and spatial resolution of bimodal imaging. The binomial approximation of the stiffness weight function was shown to introduce negligible error (<1%), yet it can be used to derive bimodal AFM theory without invoking the use of fractional calculus.
The experimental in situ determination of the tip shape and size is a pivotal step towards absolute quantitative nanomechanical measurements in a variety of techniques. This work demonstrates the benefits of tip characterization in the context of bimodal nanomechanical mapping, which improves the accuracy of fast parametric techniques such as AM-FM nanomechanical mapping.
Appendix
a. Correction factor for contact radius: αc
The correction factor that accounts for deformation of the sample that leads to a true contact radius different from the nominal contact radius [68,69] is given by
where Γ is the gamma function. Figure 1 graphs αc for values between m = 1 and m = 2. Note that obtaining αc = 1 at the value at m = 1 requires a taking a limit.
b. Weighted interaction stiffness of the higher eigenmode
The weighted integral used to average the interaction stiffness across one oscillation cycle of the first eigenmode (Equation 6) also applies to higher eigenmodes; it can be rewritten as
where u’ is the normalized deflection of the higher eigenmode in this context. The major distinction between Equation 6 and Equation 21 is the substitution δmax → δ(t) which accounts for the non-zero amplitude of the first eigenmode A1 that introduces a time-varying component to the kint experienced by the higher mode. For a first-mode period T = 1/fc1, this effect can be averaged over a full cycle by
In the limit that A2 → 0 and fc2/fc1 → ∞, kint remains constant throughout any full oscillation cycle of the second mode, such that Equation 22 solves to
Notably, this integral that determines Δk2 only depends on the trajectory of the first eigenmode because A2 is assumed small.
c. Correction factor for power-law force model: β
When integrating kint(δ) in Equation 6 and Equation 10 to obtain Δk1 and Δk2, respectively, for a power-law model as defined by Equation 5, gamma functions emerge due to the integration of non-integer powers. They are summarized here as
Note that the gamma functions that compose αc in Appendix a relate to deformation of the sample and have no direct relationship to the gamma functions of β, which relate to the effects of power-law stiffness profiles affecting the cantilever parameters.
d. Generalized SHO equation
The on-resonance Equations 17–19 are special cases of the general solution to a simple harmonic oscillator model, which can be driven on or off resonance with concurrent changes in drive frequency, phase, oscillation amplitude and drive amplitude. This section derives a general equation that makes no assumption about which of these variables is held fixed upon interaction with the sample.
The response of a freely vibrating cantilever with effective stiffness kc, mass mc, and damping bc can be described by the complex-valued cantilever impedance [70]
where the angular frequency is defined as ω = 2πf. The subscript “c” reminds that kc, mc, bc are properties of the cantilever (prior to the tip–sample interaction) that do not change throughout the experiment.
A “reference” measurement of this cantilever impedance can be made prior to tip–sample interaction by exciting the cantilever sinusoidally with some reference driving force Fr at some reference drive frequency ωr, which results in a reference oscillation amplitude Ar and a reference phase :
The reference driving force can be defined by isolating the imaginary components of both equations and solving for the driving force:
In the presence of some interaction, the cantilever impedance is subject to a time-averaged change in stiffness Δk and a time-averaged change in damping Δb, such that the interaction impedance
The interaction impedance is inferred during the experiment by
where the drive force F, the drive frequency ω, the oscillation amplitude A and the phase response are measured during tip–sample interaction.
Subtracting the reference measurement from the interaction measurement
, then isolating the real components and solving for Δk leads to
Assuming that the drive force F is proportional to the drive amplitude D and that their relationship is frequency-independent implies that
Substituting Equation 27 and Equation 31 into Equation 30 results in
With the substitutions
and
that introduce the cantilever resonance frequency ωc and the quality factor Qc, Equation 32 can be rewritten in a more experimentally friendly form as
Lastly, driving the cantilever on resonance prior to tip sample interactions (ωr = ωc; = 90°) simplifies the result to
For AM operation, setting D = Dr and ω = ωc results in Equation 17.
For PM operation, setting A = Ar and ω = ωc results in Equation 18.
For FM operation, setting A = Ar, enforcing = 90°, and applying a binomial approximation results in Equation 19.
References
-
Binnig, G.; Quate, C. F.; Gerber, C. Phys. Rev. Lett. 1986, 56, 930. doi:10.1103/PhysRevLett.56.930
Return to citation in text: [1] [2] -
Butt, H.-J.; Cappella, B.; Kappl, M. Surf. Sci. Rep. 2005, 59, 1. doi:10.1016/j.surfrep.2005.08.003
Return to citation in text: [1] -
Cappella, B.; Dietler, G. Surf. Sci. Rep. 1999, 34, 1. doi:10.1016/S0167-5729(99)00003-5
Return to citation in text: [1] -
Killgore, J. P.; Yablon, D. G.; Tsou, A. H.; Gannepalli, A.; Yuya, P. A.; Turner, J. A.; Proksch, R.; Hurley, D. C. Langmuir 2011, 27, 13983. doi:10.1021/la203434w
Return to citation in text: [1] -
Rabe, U.; Amelio, S.; Kester, E.; Scherer, V.; Hirsekorn, S.; Arnold, W. Ultrasonics 2000, 38, 430. doi:10.1016/S0041-624X(99)00207-3
Return to citation in text: [1] -
Maivald, P.; Butt, H. J.; Gould, S. A. C.; Prater, C. B.; Drake, B.; Gurley, J. A.; Elings, V. B.; Hansma, P. K. Nanotechnology 1991, 2, 103. doi:10.1088/0957-4484/2/2/004
Return to citation in text: [1] [2] -
Radmacher, M.; Tillmann, R. W.; Gaub, H. E. Biophys. J. 1993, 64, 735. doi:10.1016/S0006-3495(93)81433-4
Return to citation in text: [1] [2] -
Tamayo, J.; García, R. Langmuir 1996, 12, 4430. doi:10.1021/la960189l
Return to citation in text: [1] -
Magonov, S. N.; Elings, V.; Whangbo, M.-H. Surf. Sci. 1997, 375, L385. doi:10.1016/S0039-6028(96)01591-9
Return to citation in text: [1] -
Proksch, R.; Yablon, D. G. Appl. Phys. Lett. 2012, 100, 073106. doi:10.1063/1.3675836
Return to citation in text: [1] [2] -
Carpick, R. W.; Salmeron, M. Chem. Rev. 1997, 97, 1163. doi:10.1021/cr960068q
Return to citation in text: [1] -
Braunsmann, C.; Proksch, R.; Revenko, I.; Schäffer, T. E. Polymer 2014, 55, 219. doi:10.1016/j.polymer.2013.11.029
Return to citation in text: [1] -
Ge, S.; Pu, Y.; Zhang, W.; Rafailovich, M.; Sokolov, J.; Buenviaje, C.; Buckmaster, R.; Overney, R. M. Phys. Rev. Lett. 2000, 85, 2340. doi:10.1103/PhysRevLett.85.2340
Return to citation in text: [1] -
Rosa-Zeiser, A.; Weilandt, E.; Hild, S.; Marti, O. Meas. Sci. Technol. 1997, 8, 1333. doi:10.1088/0957-0233/8/11/020
Return to citation in text: [1] -
Sahin, O.; Magonov, S.; Su, C.; Quate, C. F.; Solgaard, O. Nat. Nanotechnol. 2007, 2, 507. doi:10.1038/nnano.2007.226
Return to citation in text: [1] -
Hu, S.; Raman, A. Nanotechnology 2008, 19, 375704. doi:10.1088/0957-4484/19/37/375704
Return to citation in text: [1] -
Zhong, Q.; Inniss, D.; Kjoller, K.; Elings, V. B. Surf. Sci. 1993, 290, L688. doi:10.1016/0167-2584(93)90906-Y
Return to citation in text: [1] -
Hölscher, H. Appl. Phys. Lett. 2006, 89, 123109. doi:10.1063/1.2355437
Return to citation in text: [1] [2] -
Katan, A. J.; van Es, M. H.; Oosterkamp, T. H. Nanotechnology 2009, 20, 165703. doi:10.1088/0957-4484/20/16/165703
Return to citation in text: [1] [2] -
Lee, M.; Jhe, W. Phys. Rev. Lett. 2006, 97, 036104. doi:10.1103/PhysRevLett.97.036104
Return to citation in text: [1] -
Cleveland, J. P.; Anczykowski, B.; Schmid, A. E.; Elings, V. B. Appl. Phys. Lett. 1998, 72, 2613. doi:10.1063/1.121434
Return to citation in text: [1] -
San Paulo, Á.; García, R. Phys. Rev. B 2002, 66, 041406. doi:10.1103/PhysRevB.66.041406
Return to citation in text: [1] -
Albrecht, T. R.; Grütter, P.; Horne, D.; Rugar, D. J. Appl. Phys. 1991, 69, 668. doi:10.1063/1.347347
Return to citation in text: [1] [2] -
Martin, Y.; Williams, C. C.; Wickramasinghe, H. K. J. Appl. Phys. 1987, 61, 4723. doi:10.1063/1.338807
Return to citation in text: [1] -
Jesse, S.; Kalinin, S. V.; Proksch, R.; Baddorf, A. P.; Rodriguez, B. J. Nanotechnology 2007, 18, 435503. doi:10.1088/0957-4484/18/43/435503
Return to citation in text: [1] -
Forchheimer, D.; Platz, D.; Tholén, E. A.; Haviland, D. B. Phys. Rev. B 2012, 85, 195449. doi:10.1103/PhysRevB.85.195449
Return to citation in text: [1] -
Oliver, W. C.; Pharr, G. M. J. Mater. Res. 1992, 7, 1564. doi:10.1557/JMR.1992.1564
Return to citation in text: [1] [2] -
Kawai, S.; Glatzel, T.; Koch, S.; Such, B.; Baratoff, A.; Meyer, E. Phys. Rev. Lett. 2009, 103, 220801. doi:10.1103/PhysRevLett.103.220801
Return to citation in text: [1] -
Li, J. W.; Cleveland, J. P.; Proksch, R. Appl. Phys. Lett. 2009, 94, 163118. doi:10.1063/1.3126521
Return to citation in text: [1] -
Stark, R. W. Appl. Phys. Lett. 2009, 94, 063109. doi:10.1063/1.3080209
Return to citation in text: [1] -
Ebeling, D.; Solares, S. D. Nanotechnology 2013, 24, 135702. doi:10.1088/0957-4484/24/13/135702
Return to citation in text: [1] -
Rodríguez, T. R.; García, R. Appl. Phys. Lett. 2004, 84, 449. doi:10.1063/1.1642273
Return to citation in text: [1] -
Proksch, R. Appl. Phys. Lett. 2006, 89, 113121. doi:10.1063/1.2345593
Return to citation in text: [1] [2] -
Solares, S. D.; Chawla, G. Meas. Sci. Technol. 2010, 21, 125502. doi:10.1088/0957-0233/21/12/125502
Return to citation in text: [1] -
Lozano, J. R.; Garcia, R. Phys. Rev. Lett. 2008, 100, 076102. doi:10.1103/PhysRevLett.100.076102
Return to citation in text: [1] -
Sader, J. E.; Jarvis, S. P. Appl. Phys. Lett. 2004, 84, 1801. doi:10.1063/1.1667267
Return to citation in text: [1] [2] -
Herruzo, E. T.; Garcia, R. Appl. Phys. Lett. 2007, 91, 143113. doi:10.1063/1.2794426
Return to citation in text: [1] -
Herruzo, E. T.; Garcia, R. Beilstein J. Nanotechnol. 2012, 3, 198. doi:10.3762/bjnano.3.22
Return to citation in text: [1] [2] -
Herruzo, E. T.; Perrino, A. P.; Garcia, R. Nat. Commun. 2014, 5, 3126. doi:10.1038/ncomms4126
Return to citation in text: [1] [2] [3] [4] -
Sader, J. E.; Uchihashi, T.; Higgins, M. J.; Farrell, A.; Nakayama, Y.; Jarvis, S. P. Nanotechnology 2005, 16, S94. doi:10.1088/0957-4484/16/3/018
Return to citation in text: [1] -
Aksoy, M. D.; Atalar, A. Phys. Rev. B 2011, 83, 075416. doi:10.1103/PhysRevB.83.075416
Return to citation in text: [1] -
García, R.; Pérez, R. Surf. Sci. Rep. 2002, 47, 197. doi:10.1016/S0167-5729(02)00077-8
Return to citation in text: [1] -
Labuda, A.; Kobayashi, K.; Kiracofe, D.; Suzuki, K.; Grütter, P. H.; Yamada, H. AIP Adv. 2011, 1, 022136. doi:10.1063/1.3601872
Return to citation in text: [1] [2] -
Fukuma, T.; Kilpatrick, J. I.; Jarvis, S. P. Rev. Sci. Instrum. 2006, 77, 123703. doi:10.1063/1.2405361
Return to citation in text: [1] -
Hölscher, H. J. Appl. Phys. 2008, 103, 064317. doi:10.1063/1.2896450
Return to citation in text: [1] -
Sugawara, Y.; Kobayashi, N.; Kawakami, M.; Li, Y. J.; Naitoh, Y.; Kageshima, M. Appl. Phys. Lett. 2007, 90, 194104. doi:10.1063/1.2737907
Return to citation in text: [1] -
Labuda, A.; Miyahara, Y.; Cockins, L.; Grütter, P. H. Phys. Rev. B 2011, 84, 125433. doi:10.1103/PhysRevB.84.125433
Return to citation in text: [1] -
Johnson, K. L. Contact Mechanics; Cambridge University Press: Cambridge, United Kingdom, 1985.
Return to citation in text: [1] -
Sneddon, I. N. Int. J. Eng. Sci. 1965, 3, 47. doi:10.1016/0020-7225(65)90019-4
Return to citation in text: [1] -
Giessibl, F. J. Appl. Phys. Lett. 2001, 78, 123. doi:10.1063/1.1335546
Return to citation in text: [1] -
Dürig, U. Appl. Phys. Lett. 2000, 76, 1203. doi:10.1063/1.125983
Return to citation in text: [1] -
Martinez, N. F.; Patil, S.; Lozano, J. R.; Garcia, R. Appl. Phys. Lett. 2006, 89, 153115. doi:10.1063/1.2360894
Return to citation in text: [1] -
Gotsmann, B.; Fuchs, H. Appl. Surf. Sci. 2002, 188, 355. doi:10.1016/S0169-4332(01)00950-3
Return to citation in text: [1] -
Ebeling, D.; Solares, S. D. Beilstein J. Nanotechnol. 2013, 4, 198. doi:10.3762/bjnano.4.20
Return to citation in text: [1] -
Garcia, R.; Herruzo, E. T. Nat. Nanotechnol. 2012, 7, 217. doi:10.1038/nnano.2012.38
Return to citation in text: [1] -
Labuda, A.; Cleveland, J.; Geisse, N.; Kocun, M.; Ohler, B.; Proksch, R.; Viani, M.; Walters, D. Microsc. Anal. 2014, 28, 23.
Return to citation in text: [1] -
Labuda, A.; Kobayashi, K.; Miyahara, Y.; Grütter, P. Rev. Sci. Instrum. 2012, 83, 053703. doi:10.1063/1.4712286
Return to citation in text: [1] -
Proksch, R.; Kalinin, S. V. Nanotechnology 2010, 21, 455705. doi:10.1088/0957-4484/21/45/455705
Return to citation in text: [1] -
Labuda, A.; Brastaviceanu, T.; Pavlov, I.; Paul, W.; Rassier, D. E. Rev. Sci. Instrum. 2011, 82, 013701. doi:10.1063/1.3527913
Return to citation in text: [1] -
Kobayashi, K.; Yamada, H.; Matsushige, K. Rev. Sci. Instrum. 2011, 82, 033702. doi:10.1063/1.3557416
Return to citation in text: [1] -
Sader, J. E.; Sanelli, J. A.; Adamson, B. D.; Monty, J. P.; Wei, X.; Crawford, S. A.; Friend, J. R.; Marusic, I.; Mulvaney, P.; Bieske, E. J. Rev. Sci. Instrum. 2012, 83, 103705. doi:10.1063/1.4757398
Return to citation in text: [1] -
Labuda, A.; Kocun, M.; Lysy, M.; Walsh, T.; Meinhold, J.; Proksch, T.; Meinhold, W.; Anderson, C.; Proksch, R. Rev. Sci. Instrum. 2016, 87, in press. doi:10.1063/1.4955122
Return to citation in text: [1] -
Labuda, A. Rev. Sci. Instrum. 2016, 87, 033704. doi:10.1063/1.4943292
Return to citation in text: [1] -
Hutter, J. L.; Bechhoefer, J. Rev. Sci. Instrum. 1993, 64, 1868. doi:10.1063/1.1143970
Return to citation in text: [1] -
Butt, H.-J.; Jaschke, M. Nanotechnology 1995, 6, 1. doi:10.1088/0957-4484/6/1/001
Return to citation in text: [1] -
Higgins, M. J.; Proksch, R.; Sader, J. E.; Polcik, M.; Mc Endoo, S.; Cleveland, J. P.; Jarvis, S. P. Rev. Sci. Instrum. 2006, 77, 013701. doi:10.1063/1.2162455
Return to citation in text: [1] -
Miyake, K.; Satomi, N.; Sasaki, S. Appl. Phys. Lett. 2006, 89, 031925. doi:10.1063/1.2234648
Return to citation in text: [1] -
Popov, V. L. Friction 2013, 1, 41. doi:10.1007/s40544-013-0005-3
Return to citation in text: [1] -
Heß, M. Phys. Mesomech. 2012, 15, 264. doi:10.1134/S1029959912030034
Return to citation in text: [1] -
Labuda, A.; Grütter, P. Langmuir 2012, 28, 5319. doi:10.1021/la300557u
Return to citation in text: [1]
| 23. | Albrecht, T. R.; Grütter, P.; Horne, D.; Rugar, D. J. Appl. Phys. 1991, 69, 668. doi:10.1063/1.347347 |
| 36. | Sader, J. E.; Jarvis, S. P. Appl. Phys. Lett. 2004, 84, 1801. doi:10.1063/1.1667267 |
| 47. | Labuda, A.; Miyahara, Y.; Cockins, L.; Grütter, P. H. Phys. Rev. B 2011, 84, 125433. doi:10.1103/PhysRevB.84.125433 |
| 48. | Johnson, K. L. Contact Mechanics; Cambridge University Press: Cambridge, United Kingdom, 1985. |
| 49. | Sneddon, I. N. Int. J. Eng. Sci. 1965, 3, 47. doi:10.1016/0020-7225(65)90019-4 |
| 39. | Herruzo, E. T.; Perrino, A. P.; Garcia, R. Nat. Commun. 2014, 5, 3126. doi:10.1038/ncomms4126 |
| 55. | Garcia, R.; Herruzo, E. T. Nat. Nanotechnol. 2012, 7, 217. doi:10.1038/nnano.2012.38 |
| 52. | Martinez, N. F.; Patil, S.; Lozano, J. R.; Garcia, R. Appl. Phys. Lett. 2006, 89, 153115. doi:10.1063/1.2360894 |
| 53. | Gotsmann, B.; Fuchs, H. Appl. Surf. Sci. 2002, 188, 355. doi:10.1016/S0169-4332(01)00950-3 |
| 54. | Ebeling, D.; Solares, S. D. Beilstein J. Nanotechnol. 2013, 4, 198. doi:10.3762/bjnano.4.20 |
| 39. | Herruzo, E. T.; Perrino, A. P.; Garcia, R. Nat. Commun. 2014, 5, 3126. doi:10.1038/ncomms4126 |
| 27. | Oliver, W. C.; Pharr, G. M. J. Mater. Res. 1992, 7, 1564. doi:10.1557/JMR.1992.1564 |
| 56. | Labuda, A.; Cleveland, J.; Geisse, N.; Kocun, M.; Ohler, B.; Proksch, R.; Viani, M.; Walters, D. Microsc. Anal. 2014, 28, 23. |
| 57. | Labuda, A.; Kobayashi, K.; Miyahara, Y.; Grütter, P. Rev. Sci. Instrum. 2012, 83, 053703. doi:10.1063/1.4712286 |
| 58. | Proksch, R.; Kalinin, S. V. Nanotechnology 2010, 21, 455705. doi:10.1088/0957-4484/21/45/455705 |
| 59. | Labuda, A.; Brastaviceanu, T.; Pavlov, I.; Paul, W.; Rassier, D. E. Rev. Sci. Instrum. 2011, 82, 013701. doi:10.1063/1.3527913 |
| 60. | Kobayashi, K.; Yamada, H.; Matsushige, K. Rev. Sci. Instrum. 2011, 82, 033702. doi:10.1063/1.3557416 |
| 68. | Popov, V. L. Friction 2013, 1, 41. doi:10.1007/s40544-013-0005-3 |
| 69. | Heß, M. Phys. Mesomech. 2012, 15, 264. doi:10.1134/S1029959912030034 |
| 67. | Miyake, K.; Satomi, N.; Sasaki, S. Appl. Phys. Lett. 2006, 89, 031925. doi:10.1063/1.2234648 |
| 38. | Herruzo, E. T.; Garcia, R. Beilstein J. Nanotechnol. 2012, 3, 198. doi:10.3762/bjnano.3.22 |
| 39. | Herruzo, E. T.; Perrino, A. P.; Garcia, R. Nat. Commun. 2014, 5, 3126. doi:10.1038/ncomms4126 |
| 64. | Hutter, J. L.; Bechhoefer, J. Rev. Sci. Instrum. 1993, 64, 1868. doi:10.1063/1.1143970 |
| 65. | Butt, H.-J.; Jaschke, M. Nanotechnology 1995, 6, 1. doi:10.1088/0957-4484/6/1/001 |
| 66. | Higgins, M. J.; Proksch, R.; Sader, J. E.; Polcik, M.; Mc Endoo, S.; Cleveland, J. P.; Jarvis, S. P. Rev. Sci. Instrum. 2006, 77, 013701. doi:10.1063/1.2162455 |
| 61. | Sader, J. E.; Sanelli, J. A.; Adamson, B. D.; Monty, J. P.; Wei, X.; Crawford, S. A.; Friend, J. R.; Marusic, I.; Mulvaney, P.; Bieske, E. J. Rev. Sci. Instrum. 2012, 83, 103705. doi:10.1063/1.4757398 |
| 62. | Labuda, A.; Kocun, M.; Lysy, M.; Walsh, T.; Meinhold, J.; Proksch, T.; Meinhold, W.; Anderson, C.; Proksch, R. Rev. Sci. Instrum. 2016, 87, in press. doi:10.1063/1.4955122 |
| 1. | Binnig, G.; Quate, C. F.; Gerber, C. Phys. Rev. Lett. 1986, 56, 930. doi:10.1103/PhysRevLett.56.930 |
| 8. | Tamayo, J.; García, R. Langmuir 1996, 12, 4430. doi:10.1021/la960189l |
| 9. | Magonov, S. N.; Elings, V.; Whangbo, M.-H. Surf. Sci. 1997, 375, L385. doi:10.1016/S0039-6028(96)01591-9 |
| 6. | Maivald, P.; Butt, H. J.; Gould, S. A. C.; Prater, C. B.; Drake, B.; Gurley, J. A.; Elings, V. B.; Hansma, P. K. Nanotechnology 1991, 2, 103. doi:10.1088/0957-4484/2/2/004 |
| 7. | Radmacher, M.; Tillmann, R. W.; Gaub, H. E. Biophys. J. 1993, 64, 735. doi:10.1016/S0006-3495(93)81433-4 |
| 6. | Maivald, P.; Butt, H. J.; Gould, S. A. C.; Prater, C. B.; Drake, B.; Gurley, J. A.; Elings, V. B.; Hansma, P. K. Nanotechnology 1991, 2, 103. doi:10.1088/0957-4484/2/2/004 |
| 7. | Radmacher, M.; Tillmann, R. W.; Gaub, H. E. Biophys. J. 1993, 64, 735. doi:10.1016/S0006-3495(93)81433-4 |
| 23. | Albrecht, T. R.; Grütter, P.; Horne, D.; Rugar, D. J. Appl. Phys. 1991, 69, 668. doi:10.1063/1.347347 |
| 4. | Killgore, J. P.; Yablon, D. G.; Tsou, A. H.; Gannepalli, A.; Yuya, P. A.; Turner, J. A.; Proksch, R.; Hurley, D. C. Langmuir 2011, 27, 13983. doi:10.1021/la203434w |
| 5. | Rabe, U.; Amelio, S.; Kester, E.; Scherer, V.; Hirsekorn, S.; Arnold, W. Ultrasonics 2000, 38, 430. doi:10.1016/S0041-624X(99)00207-3 |
| 18. | Hölscher, H. Appl. Phys. Lett. 2006, 89, 123109. doi:10.1063/1.2355437 |
| 19. | Katan, A. J.; van Es, M. H.; Oosterkamp, T. H. Nanotechnology 2009, 20, 165703. doi:10.1088/0957-4484/20/16/165703 |
| 20. | Lee, M.; Jhe, W. Phys. Rev. Lett. 2006, 97, 036104. doi:10.1103/PhysRevLett.97.036104 |
| 2. | Butt, H.-J.; Cappella, B.; Kappl, M. Surf. Sci. Rep. 2005, 59, 1. doi:10.1016/j.surfrep.2005.08.003 |
| 3. | Cappella, B.; Dietler, G. Surf. Sci. Rep. 1999, 34, 1. doi:10.1016/S0167-5729(99)00003-5 |
| 10. | Proksch, R.; Yablon, D. G. Appl. Phys. Lett. 2012, 100, 073106. doi:10.1063/1.3675836 |
| 21. | Cleveland, J. P.; Anczykowski, B.; Schmid, A. E.; Elings, V. B. Appl. Phys. Lett. 1998, 72, 2613. doi:10.1063/1.121434 |
| 22. | San Paulo, Á.; García, R. Phys. Rev. B 2002, 66, 041406. doi:10.1103/PhysRevB.66.041406 |
| 13. | Ge, S.; Pu, Y.; Zhang, W.; Rafailovich, M.; Sokolov, J.; Buenviaje, C.; Buckmaster, R.; Overney, R. M. Phys. Rev. Lett. 2000, 85, 2340. doi:10.1103/PhysRevLett.85.2340 |
| 15. | Sahin, O.; Magonov, S.; Su, C.; Quate, C. F.; Solgaard, O. Nat. Nanotechnol. 2007, 2, 507. doi:10.1038/nnano.2007.226 |
| 12. | Braunsmann, C.; Proksch, R.; Revenko, I.; Schäffer, T. E. Polymer 2014, 55, 219. doi:10.1016/j.polymer.2013.11.029 |
| 16. | Hu, S.; Raman, A. Nanotechnology 2008, 19, 375704. doi:10.1088/0957-4484/19/37/375704 |
| 17. | Zhong, Q.; Inniss, D.; Kjoller, K.; Elings, V. B. Surf. Sci. 1993, 290, L688. doi:10.1016/0167-2584(93)90906-Y |
| 11. | Carpick, R. W.; Salmeron, M. Chem. Rev. 1997, 97, 1163. doi:10.1021/cr960068q |
| 10. | Proksch, R.; Yablon, D. G. Appl. Phys. Lett. 2012, 100, 073106. doi:10.1063/1.3675836 |
| 14. | Rosa-Zeiser, A.; Weilandt, E.; Hild, S.; Marti, O. Meas. Sci. Technol. 1997, 8, 1333. doi:10.1088/0957-0233/8/11/020 |
| 26. | Forchheimer, D.; Platz, D.; Tholén, E. A.; Haviland, D. B. Phys. Rev. B 2012, 85, 195449. doi:10.1103/PhysRevB.85.195449 |
| 24. | Martin, Y.; Williams, C. C.; Wickramasinghe, H. K. J. Appl. Phys. 1987, 61, 4723. doi:10.1063/1.338807 |
| 25. | Jesse, S.; Kalinin, S. V.; Proksch, R.; Baddorf, A. P.; Rodriguez, B. J. Nanotechnology 2007, 18, 435503. doi:10.1088/0957-4484/18/43/435503 |
| 1. | Binnig, G.; Quate, C. F.; Gerber, C. Phys. Rev. Lett. 1986, 56, 930. doi:10.1103/PhysRevLett.56.930 |
| 18. | Hölscher, H. Appl. Phys. Lett. 2006, 89, 123109. doi:10.1063/1.2355437 |
| 19. | Katan, A. J.; van Es, M. H.; Oosterkamp, T. H. Nanotechnology 2009, 20, 165703. doi:10.1088/0957-4484/20/16/165703 |
| 43. | Labuda, A.; Kobayashi, K.; Kiracofe, D.; Suzuki, K.; Grütter, P. H.; Yamada, H. AIP Adv. 2011, 1, 022136. doi:10.1063/1.3601872 |
| 44. | Fukuma, T.; Kilpatrick, J. I.; Jarvis, S. P. Rev. Sci. Instrum. 2006, 77, 123703. doi:10.1063/1.2405361 |
| 45. | Hölscher, H. J. Appl. Phys. 2008, 103, 064317. doi:10.1063/1.2896450 |
| 46. | Sugawara, Y.; Kobayashi, N.; Kawakami, M.; Li, Y. J.; Naitoh, Y.; Kageshima, M. Appl. Phys. Lett. 2007, 90, 194104. doi:10.1063/1.2737907 |
| 36. | Sader, J. E.; Jarvis, S. P. Appl. Phys. Lett. 2004, 84, 1801. doi:10.1063/1.1667267 |
| 37. | Herruzo, E. T.; Garcia, R. Appl. Phys. Lett. 2007, 91, 143113. doi:10.1063/1.2794426 |
| 38. | Herruzo, E. T.; Garcia, R. Beilstein J. Nanotechnol. 2012, 3, 198. doi:10.3762/bjnano.3.22 |
| 39. | Herruzo, E. T.; Perrino, A. P.; Garcia, R. Nat. Commun. 2014, 5, 3126. doi:10.1038/ncomms4126 |
| 40. | Sader, J. E.; Uchihashi, T.; Higgins, M. J.; Farrell, A.; Nakayama, Y.; Jarvis, S. P. Nanotechnology 2005, 16, S94. doi:10.1088/0957-4484/16/3/018 |
| 41. | Aksoy, M. D.; Atalar, A. Phys. Rev. B 2011, 83, 075416. doi:10.1103/PhysRevB.83.075416 |
| 42. | García, R.; Pérez, R. Surf. Sci. Rep. 2002, 47, 197. doi:10.1016/S0167-5729(02)00077-8 |
| 43. | Labuda, A.; Kobayashi, K.; Kiracofe, D.; Suzuki, K.; Grütter, P. H.; Yamada, H. AIP Adv. 2011, 1, 022136. doi:10.1063/1.3601872 |
| 34. | Solares, S. D.; Chawla, G. Meas. Sci. Technol. 2010, 21, 125502. doi:10.1088/0957-0233/21/12/125502 |
| 35. | Lozano, J. R.; Garcia, R. Phys. Rev. Lett. 2008, 100, 076102. doi:10.1103/PhysRevLett.100.076102 |
| 27. | Oliver, W. C.; Pharr, G. M. J. Mater. Res. 1992, 7, 1564. doi:10.1557/JMR.1992.1564 |
| 28. | Kawai, S.; Glatzel, T.; Koch, S.; Such, B.; Baratoff, A.; Meyer, E. Phys. Rev. Lett. 2009, 103, 220801. doi:10.1103/PhysRevLett.103.220801 |
| 29. | Li, J. W.; Cleveland, J. P.; Proksch, R. Appl. Phys. Lett. 2009, 94, 163118. doi:10.1063/1.3126521 |
| 30. | Stark, R. W. Appl. Phys. Lett. 2009, 94, 063109. doi:10.1063/1.3080209 |
| 31. | Ebeling, D.; Solares, S. D. Nanotechnology 2013, 24, 135702. doi:10.1088/0957-4484/24/13/135702 |
| 32. | Rodríguez, T. R.; García, R. Appl. Phys. Lett. 2004, 84, 449. doi:10.1063/1.1642273 |
| 33. | Proksch, R. Appl. Phys. Lett. 2006, 89, 113121. doi:10.1063/1.2345593 |
© 2016 Labuda et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Nanotechnology terms and conditions: (http://www.beilstein-journals.org/bjnano)