Abstract
During the past five years, it has been shown that carbon nanotubes act as an exceptional reinforcement for composites. For this reason, a large number of investigations have been devoted to analysis of fundamental, structural behavior of solid structures made of carbon-nanotube-reinforced composites (CNTRC). The present research, as an extension of the available works on the vibration analysis of CNTRC structures, examines the free vibration characteristics of plates containing a cutout that are reinforced with uniform or nonuniform distribution of carbon nanotubes. The first-order shear deformation plate theory is used to estimate the kinematics of the plate. The solution method is based on the Ritz method with Chebyshev basis polynomials. Such a solution method is suitable for arbitrary in-plane and out-of-plane boundary conditions of the plate. It is shown that through a functionally graded distribution of carbon nanotubes across the thickness of the plate, the fundamental frequency of a rectangular plate with or without a cutout may be enhanced. Furthermore, the frequencies are highly dependent on the volume fraction of carbon nanotubes and may be increased upon using more carbon nanotubes as reinforcement.
Introduction
Plates with cutouts are extensively used in automotive and aircraft structures. Cutouts may be of rectangular, circular, elliptical, super elliptical or polygonal shape. Due to the complicated configuration of a plate with a cutout, there is significantly less research on plates with cutouts in comparison to those without cut-out. Depending on the application, homogeneous isotropic, composite or functionally graded plates may be perforated to fulfill a desired application.
Representing a type of novel material with fascinating electro-thermo-mechanical properties, carbon nanotubes (CNTs) have attracted increasing attention in the past decades. CNTs are a promising candidate for the reinforcement of the matrix phase in a composite. Kwon et al. [1] reported that using a powder metallurgy fabrication process, carbon-nanotube-reinforced composites (CNTRCs) may be achieved with a nonuniform distribution of CNTs through the media. This type of reinforced composite media is known as functionally graded carbon-nanotube-reinforced composite (FG-CNTRC). An overview on the properties, modeling and characteristics of FG-CNTRC beams, plates and shells is provided by Liew et al. [2]
It has been shown that the bending moment may be significantly alleviated through a functionally graded distribution of CNTs in a polymeric matrix [3]. In the five years following the discovery of this interesting feature, various investigations were reported on the mechanics of FG-CNTRC structures.
Zhu et al. [4] investigated the free vibration and static response of FG-CNTRC plates using finite element method [4]. Zhang et al. investigated the free vibration characteristics of FG-CNTRC skew plates [5], triangular plates [6] and cylindrical panels [7] using element free methods. In these works it is shown that the natural frequencies of plates and panels are affected by the distribution and volume fraction of CNTs. Zhang et al. [8] investigated the free vibration characteristics of FG-CNTRC plates resting on an elastic foundation. Lei et al. [9] investigated the free vibration of composite, laminated FG-CNTRC plates with general boundary conditions. Malekzadeh and Zarei [10] examined the free vibration characteristics of laminated plates containing FG-CNTRC layers in an arbitrary straight-sided quadrilateral shape. Malekzadeh and Heydarpour [11] investigated the free vibration and static response of laminated plates with FG-CNTRC layers using a mixed Navier-layerwise differential quadrature method. In this research, plates with all edges simply supported are considered. Natarajan et al. [12] applied a higher order shear and normal deformable plate formulation to study the static and free vibrations of single layer FG-CNTRC plates and also sandwich plates with FG-CNTRC face sheets. Wang and Shen investigated the linear and nonlinear free vibrations of a single layer FG-CNTRC plate [13] and also sandwich plates with stiff core and FG-CNTRC face sheets [14]. In this analysis, the interaction of the plate with a two parameter elastic foundation is also taken into account. Wang and Shen [15] investigated the dynamic response of FG-CNTRC plates according to the von Kármán formulation. In this research, the interaction of a two parameter elastic foundation and a thermal environment are also included. The solution method of this research is based on a two-step perturbation technique and is suitable for plates with all edges simply supported. Using a mesh-free formulation proper for arbitrary edge supports, Lei et al. [16] investigated the elasto-dynamic response of FG-CNTRC plates subjected to sudden lateral pressure. For more investigations on vibration, buckling, postbuckling, stress analysis, and nonlinear bending of FG-CNTRC plates, one may refer to [17-25].
The present research aims to investigate the free vibration characteristics of an FG-CNTRC rectangular plate containing a central, rectangular cutout. The distribution of CNTs across the plate thickness are assumed to be either uniform or nonuniform. A modified rule of mixtures approach is used to obtain the properties of the composite media. Chebyshev polynomials are used as the basic shape functions of the Ritz formulation to construct an eigenvalue problem. The solution method may be used for perforated FG-CNTRC rectangular plates with arbitrary boundary conditions on the outer edges, while the inner edges are unconstrained. The numerical results allow for the study of the volume fraction and distribution pattern of CNTs, plate boundary conditions and hole size.
Modeling
Basic formulation
A rectangular-shaped plate, made of a polymeric matrix, reinforced by CNTs whose distribution may be nonuniform, is considered in the present research. The plate contains a centered hole, which is assumed to be rectangular-shaped. The cartesian coordinate system is assigned to the center of the mid-surface of the plate. In this system, the plate occupies the domain [−0.5a 0.5a] × [−0.5b 0.5b] × [−0.5h 0.5h]. The hole occupies the domain [−0.5c 0.5c] × [−0.5d 0.5d] × [−0.5h 0.5h]. The dimensions of the plate with the assigned coordinate system are demonstrated in Figure 1.
![[2190-4286-7-45-1]](/bjnano/content/figures/2190-4286-7-45-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: A schematic of the geometric features of the plate along with the assigned coordinate system.
Figure 1: A schematic of the geometric features of the plate along with the assigned coordinate system.
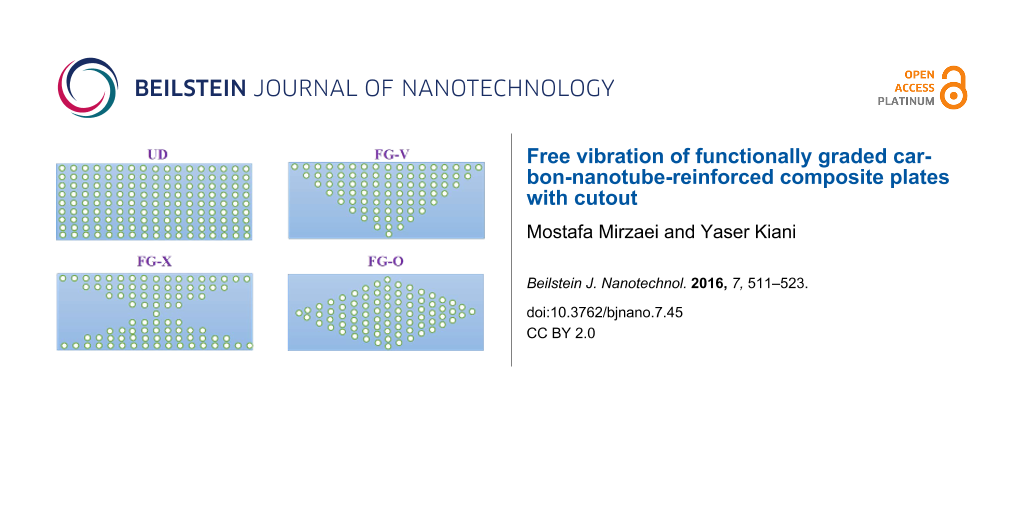
Motivated by the fundamental research of Shen [3], many investigators take into account the functionally graded distribution of the volume fraction of reinforcements through the matrix. Consistent with the possible fabrication processes for plates, three different functionally graded types of CNT dispersion profiles may be assumed and are considered in the present research: FG-V, FG-O and FG-X [5-7]. A schematic of these functionally graded types along with the uniformly distributed (UD) type are shown in Figure 2.
![[2190-4286-7-45-2]](/bjnano/content/figures/2190-4286-7-45-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Various graded patterns of FG-CNTRC plates.
Figure 2: Various graded patterns of FG-CNTRC plates.
The properties of a composite media (i.e., a matrix reinforced with CNTs) may be obtained according to various homogenization techniques. The two commonly used schemes that are extensively used for composites and FGMs are the Mori–Tanaka scheme [26] and the rule of mixtures [27]. The conventional rule of mixtures has the advantage of simplicity; however, when using CNTRCs, this approach does not provide an accurate estimation of the mechanical properties of the media. Meanwhile, as explained by Shen [3] and used extensively by other researchers [28-32], the conventional rule of mixtures approach may be modified with the introduction of the efficiency parameters. Under such modification, Young’s modulus and the shear modulus of the composite media take the form:
In this formula, the properties of the CNT are denoted by a superscript CN and that those belong to matrix are denoted by a superscript m. Following the classical solid mechanics notation, E and G are the elastic modulus and shear modulus of the constituents, respectively. In comparison to the conventional rule of mixtures approach, three unknown constants, η1, η2 and η3, are introduced in Equation 1; these are known as efficiency parameters. These parameters compensate for the errors generated due to the conventional rule of mixtures approach for a CNTRC. The values of these constants are obtained by matching the data obtained according to the above formula with those obtained based on the molecular dynamics simulation.
It is worth noting that the volume fraction of CNTs and polymeric matrix are denoted by VCN and Vm, respectively. According to the partition of unity property, the following condition should be satisfied at each point of the composite media: VCN + Vm = 1.
The volume fraction of CNTs is assumed to be either nonuniform or uniform across the plate thickness. According to the above rule, the volume fraction of matrix may also be achieved and the overall properties of the media may be calculated according to Equation 1. Table 1 presents the dispersion profile of VCN as a function of the thickness coordinate for each of the UD CNTRC or FG-CNTRC rectangular plates.
Table 1: Volume fraction of CNTs as a function of the thickness coordinate for various CNT distributions [28-34].
| CNT Distribution | VCN |
|---|---|
| UD CNTRC |
|
| FG-V CNTRC |
|
| FG-O CNTRC |
|
| FG-X CNTRC |
|
Upon evaluation of the total volume fraction of CNTs across the plate thickness, it is revealed that all types have the same total volume fraction of CNTs, that is, . Consequently, the vibrational characteristics of FG-CNTRC and UD-CNTRC rectangular plates may be compared with respect to each other. As previously shown in Figure 2 and the information in Table 1, given an FG-X pattern of CNT dispersion, the mid-surface of the plate is free of CNTs while the top and bottom surfaces have the maximum volume fraction of CNTs. The volume fraction of CNTs increases linearly from the mid-plane to the free surfaces of the plate. The FG-O type of distribution pattern is the inverse of the FG-X case. In the FG-O distribution, the top and bottom surfaces are free of CNTs and the mid-surface has the maximum volume fraction of CNTs. In FG-V type, the bottom surface is free of CNTs and the top has the maximum volume fraction of CNTs. Unlike these three types, in the UD case, each surface of the plate has the same volume fraction of CNTs.
Similar to the shear modulus and Young’s modulus, Poisson’s ratio and the mass density of the composite media may be written in terms of belongings to the CNT and matrix. As claimed by Shen [28], and as used also by other researchers [29], Poisson’s ratio depends weakly on position and consequently may be obtained as
The mass density of a CNTRC media may be obtained according to the conventional rule of mixtures approach [13,14]. Therefore, as a function of volume fraction and mass density of constituents, ρCN and ρm, one may write
Upon evaluation of the mass fraction for each of the graded patterns of CNTs, it is concluded that each type has the same mass fraction of CNTs.
Flexural theories propose an approximate function for the in-plane and out-of-plane displacement components of the plate. The most simple flexural theory is the classical plate theory, which eliminates the transverse shear strain components as well as the normal strain component. These assumptions are exaggerated for moderately thick composites and therefore classical plate theory results in erroneous results for the structural response of a CNTRC rectangular plate. On the other hand, first order shear deformation plate theory (FSDT), which takes into account the constant transverse shear strain, results in accurate results for the global properties of moderately thick CNTRC plates. This is because it takes into account both the rotary inertias and through-the-thickness shear strains [35]. This research is also developed based on FSDT, which estimates the displacements of the plate in terms of those of the mid-surface and the cross-section rotations as
In Equation 4, the subscript zero indicates the characteristics of the mid-plane. Rotations of the cross-sectional elements about the x and y axes are denoted by φy and φx. Additionally, displacements along the x, y and z directions are shown by u, v and w.
The substitution of Equation 4 into the strain–displacement relations results in the components of strain on an arbitrary point of the plate in terms of mid-surface strain components and change in curvature as
The strain field on the midsurface of the plate may be obtained according to the midsurface displacements as
and the change of curvatures may be obtained in terms of cross-section rotations as
where in Equation 6 and Equation 7 (and hereafter), the comma in the subscript indicates the derivative with respect to the variable following the comma.
Under linear elastic behavior of the composite media, the strain components may be obtained in terms of strain components according to the following generalized Hook law as
where the plane-stress stiffnesses of the plate are denote by Qij components (i,j = 1,2,4,5,6). These constants may be obtained in terms of the Poisson’s ratio, shear modulus and Young’s modulus of the composite plate as [29]
To construct the motion equations of the plate, the Hamilton principle may be used [35]. For free vibration analysis where external forces/moments are absent, Hamilton’s principle may be written as
where δU is the virtual strain energy of the perforated plate which may be calculated as
In the above equation and in the rest of this work, the subscripts 1 and 2 denote a solid rectangle (i.e., a solid rectangle without a cutout) and the cutout segment, respectively. The strain energies may be obtained upon integration of the density of the strain energy over the suitable volume.
where the shear correction factor is denoted by κ. This parameter is used to compensate for the errors due to the assumption of constant shear strains across the thickness. The exact value of this factor is not straightforward and may be obtained under evaluation of complicated integrals. Since the exact value of this factor depends on the boundary conditions, geometry of the media, material and loading, the approximate value of κ = 5/6 is used in the present research.
Similarly, δT is the variation of the kinetic energy of the plate which also may be written as
where the kinetic energy may be obtained as
Solution procedure
It is known that the equations of motion for a plate with three translational motion and two rotational motion components may be achieved using the process of virtual displacements with the aid of the Green–Gauss theorem. On the other hand, the matrix representation of the equations of motion may be established using the application of energy methods to Equation 10. As one of the most widely known energy-based methods, the Ritz method is used in the present research. The effectiveness and efficiency of various types of Ritz methods has been the subject of many studies [36-39]. In this study, the approximation of the displacement field is carried out using the Ritz method whose shape functions are written in terms of the Chebyshev polynomials. As a result, the essential variables may be written as
In Equation 15, the i-th Chebyshev polynomial of the first kind is denoted by Pi. These functions in a closed-form expression may be written as
Additionally, in Equation 15, the auxiliary functions (Rα(x,y), where α = u,v,w,x,y) are called the boundary functions, which are associated with the essential boundary conditions. It is known that in the Ritz method, the shape functions should at least satisfy the essential boundary conditions.
Three types of mechanical boundary conditions are widely used for each of the edges of the plate: clamped (C), simply supported (S) and free (F) edges are the assumed types of boundary conditions in the present study. For a clamped edge, three components of the displacement field and two components of the rotation should be zero at the edge. For a simply supported one, the tangential displacement, tangential rotation and lateral displacement should be zero. Finally, for a free edge, none of the boundary conditions are applied, and therefore, none of the displacements and rotations are restrained at the edge. On each exterior edge of the plate, various boundary conditions may be defined; however, the interior edges are all assumed to be free and none of the boundary conditions around the hole are applied.
Since the Chebyshev polynomials of the fist kind are nonzero on both ends of the interval (i.e., Pi(±1) ≠ 0), the auxiliary functions Rα, α = u,v,w,x,y should be chosen to satisfy the essential boundary conditions on the edge when necessary. Each of the auxiliary functions Rα, α = u,v,w,x,y may be written generally as
The newly introduced parameters, p, q, r and s, are equal to zero or one and their magnitude depends on the essential boundary conditions at the edge. As an example, consider a perforated plate with clamped boundary conditions at x = −0.5a and x = +0.5a, free at y = −0.5b, and simply supported at y = +0.5b. For such a case, the auxiliary functions (Rα, where α = u,v,w,x,y) are given as
Finally, the substitution of the series expansion of Equation 15 into Equation 12 and Equation 14, and inserting the results into the Hamilton principle of Equation 10 results in the motion equations given as
In the above equation, M is the mass matrix and, K is the stiffness matrix. Additionally, the mechanical displacement vector is denoted by X, which consists of the unknown displacements Uij, Vij, Wij, Xij and Yij.
Since the free vibration response is under investigation, X = sin(ω t+φ) may be considered, where ω is the natural frequency. The substitution of this equation into Equation 19 results in an eigenvalue problem as
This eigenvalue problem can be solved using the standard eigenvalue algorithms provided in a Matlab code. It is worth noting that trapezoidal numerical integration is used to evaluate the elements of the mass and stiffness matrices. In numerical integration, the interval is divided into 100 segments.
Results and Discussion
The free vibration characteristics of FG-CNTRC rectangular plates with a centric rectangular hole were formulated in the previous sections. In the following, to assure the effectiveness and accuracy of the presented solution method, convergence and comparison studies are carried out. Next, parametric studies are provided to explore the effects of carbon nanotube characteristics on the frequencies of the perforated plate. The following convention is established for boundary conditions herein and is used in the rest of this work. For instance, an SCFS plate indicates a plate which is simply supported at x = −0.5a and y = +0.5b, clamped at y = −0.5b, and free at x = +0.5b.
In the numerical results of the present research, isotropic poly(methyl methacrylate), referred to as PMMA, is selected as the polymeric matrix. The mechanical properties of the PMMA are Em = 2.5 GPa, νm = 0.34 and ρm = 1150 kg/m3. Reinforcement of the matrix is chosen as (10,10)-armchair SWCNT. For this kind of reinforcement, which is orthotropic, the material properties are given as = 5.6466 TPa,
= 7.0800 TPa, G12 = 1.9445 TPa, ν = 0.175 and ρ = 1400 kg/m3 [40].
Finally, the efficiency parameters should be known to obtain the overall properties of the composite media, which are the stretching, coupling and bending stiffnesses. As mentioned before, these parameters are obtained by matching the data obtained by the present modified rule of mixtures approach and the molecular dynamics simulations of other researchers. A molecular dynamics simulation was performed by Han and Elliott [41]; however, since the condition of maximum thickness for CNTs was not satisfied in this research, their simulations were re-examined by Shen [28]. In the simulations of Han and Elliott [41], the effective thickness of the CNTs is set equal to at least 0.34 nm, which is open to criticism since it violates the criteria proposed by Wang and Zhang [42]. The molecular dynamics simulations of Shen [28] result in the following efficiency parameters for the CNTRC media that depend on the volume fraction of CNTs: η1 = 0.137 and η2 = 1.022 for = 0.12; η1 = 0.142 and η2 = 1.626 for
= 0.17; and η1 = 0.141 and η2 = 1.585 for
= 0.28. For each case, the efficiency parameter η3 is equal to 0.7η2. The shear modulus G13 is taken equal to G12, whereas G23 is taken equal to 1.2G12 [28].
Convergence and comparison studies
Convergence and comparison studies are presented in this section. First, the convergence study allows for the necessary shape functions to be obtained with the series expansion of the Ritz method, with results shown in Table 2. In this study, the first three frequency parameters of a square plate with a square cutout at the center are evaluated in terms of the number of shape functions. Two different cutout sizes are considered. The results are also compared with those of Liew et al. [43] and Lam et al. [44]. In the solution method of Liew et al. [43], the basic L-shaped element, which is divided into appropriate sub-domains that are dependent upon the location of the cutout, is used as the basic building element. Lam et al. [44], on the other hand, obtained the frequencies according to a Ritz method whose shape functions are generated using the Gram–Schmidt process. In both of the above-mentioned references, the plate is formulated using the classical plate theory and for the sake of comparison, in the present analysis, the side-to-thickness ratio is chosen as a/h = 100. It is seen that the results of our study match well with those of Liew et al. [43] and Lam et al. [44] after the adoption of Nx = Ny = 20 shape functions. Therefore, in the subsequent results, the number of shape functions in both directions is chosen as 20.
Table 2:
Convergence study on the first three frequency parameters of SSSS isotropic homogeneous square plates with a/h = 100, ν = 0.3 and two cutout ratios.
| Nx = Ny | c/a=0.5 | c/a=0.3 | ||||
|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
| 4 | 25.3219 | 67.0738 | 96.5711 | 21.2056 | 59.9002 | 91.5117 |
| 6 | 24.3337 | 52.4935 | 79.6489 | 20.7782 | 49.9952 | 76.7551 |
| 8 | 23.9120 | 48.0090 | 76.8117 | 20.3092 | 49.4326 | 76.0125 |
| 10 | 23.7717 | 44.2278 | 74.2547 | 19.9607 | 48.9185 | 75.6918 |
| 12 | 23.7394 | 42.6920 | 72.9483 | 19.8747 | 48.1375 | 75.3304 |
| 14 | 23.7177 | 42.1001 | 72.4587 | 19.8625 | 47.2216 | 74.9326 |
| 16 | 23.6514 | 41.6152 | 72.1370 | 19.7767 | 46.4394 | 74.6078 |
| 18 | 23.5996 | 41.2933 | 71.8660 | 19.7260 | 45.9450 | 74.3541 |
| 20 | 23.5641 | 41.0550 | 71.7298 | 19.6490 | 45.5670 | 74.2122 |
| Liew et al. [43] | 23.441 | 41.779 | 71.737 | 19.391 | 44.799 | 73.656 |
| Lam et al. [44] | 23.235 | 39.712 | 69.868 | 19.357 | 44.207 | 73.906 |
In Table 3, the first four frequencies of a plate with a centric cutout clamped all around is evaluated. In this study, the plate is also a square, and for the sake of comparison, the side-to-thickness ratio is chosen as a/h = 100. Four different square cutout sizes, c/a = 0.1, 0.2, 0.3 and 0.5, are considered and in each case our results are compared with those of Malekzadeh et al. [45] and Mundkur et al. [46]. Malekzadeh et al. [45] obtained the frequencies according to a three dimensional elasticity formulation and using the Chebyshev–Ritz formulation, whereas boundary characteristics of orthogonal polynomial functions are invoked into the Ritz formulation by Mundkur et al. [46] to obtain the plate frequencies. It is seen that our results are in good agreement with those of both Malekzadeh et al. [45] and Mundkur et al. [46].
Table 3:
First four frequency parameters for square CCCC isotropic homogeneous plates with ν = 0.3, a/h = 100 and various square cutout sizes.
| c/a | Source |
|
|
|
|
|---|---|---|---|---|---|
| 0.1 | Malekzadeh et al. [45] | 36.7943 | 73.9968 | 74.0389 | 108.1382 |
| Mundkur et al. [46] | 36.5045 | 73.4142 | 73.4142 | 107.3528 | |
| Present | 36.3141 | 73.2476 | 73.2476 | 106.9850 | |
| 0.2 | Malekzadeh et al. [45] | 37.9162 | 73.8299 | 73.8882 | 105.9458 |
| Mundkur et al. [46] | 38.1073 | 73.6267 | 73.6267 | 105.4715 | |
| Present | 37.2017 | 72.7578 | 72.7578 | 104.7691 | |
| 0.3 | Malekzadeh et al. [45] | 41.6279 | 71.2093 | 71.3769 | 103.6814 |
| Mundkur et al. [46] | 41.7912 | 73.9799 | 73.9799 | 104.3388 | |
| Present | 40.9624 | 69.0943 | 69.0943 | 101.9502 | |
| 0.5 | Malekzadeh et al. [45] | 66.5457 | 79.1407 | 79.2248 | 109.2086 |
| Mundkur et al. [46] | 65.7150 | 81.6796 | 81.6796 | 110.8569 | |
| Present | 65.3050 | 77.7074 | 77.7074 | 107.5626 | |
Table 4 presents the frequencies of a thin square plate that is simply supported all around and contains a square cutout at the center. The cutout size is c/a = 0.4 and for the sake of comparison, the side-to-thickness ratio of the square plate is chosen as a/h = 100. The results of this study are compared with those of Liew et al. [43]. In the tabulated results, SS indicates the double-symmetric modes and AA indicates the double-antisymmetric modes. On the other hand, modes that are symmetric in one direction and antisymmetric on the other direction are denoted by AS. Again, it is seen that the results of our study are in good agreement with the available data, which verifies the accuracy of the present method.
Table 4:
Frequency parameters, for square SSSS isotropic homogeneous plates with a square cutout with ν = 0.3, c/a = 0.4 and a/h = 100.
The next comparison study gives the frequency parameters of the FG-CNTRC plate with clamped boundary conditions. The frequencies are evaluated from the proposed approach of our study and compared with those given by Zhu et al. [4] based on the finite elements method. It is worth noting that in the analysis of Zhu et al. [4], the matrix is made from PmPV with elasticity modulus Em = 2.1 GPa, Poisson’s ratio νm = 0.34 and mass density ρm = 1150 kg/m3. The volume fraction of CNTs is set equal to 0.17 and the dispersion pattern of the CNTs is of the FG-V type. In such case, the efficiency parameters are obtained as η1 = 0.149 and η2 = η3 = 1.381 [4]. Furthermore, G23 = G13 = G12 is assumed [4]. The frequency parameter is defined as as shown in Table 5. As can be seen, the first six frequencies are in good agreement with those obtained by Zhu et al. [4].
Table 5:
First six natural frequencies of square CCCC FG-CNTRC plates without cutout and various side-to-thickness ratios.
| a/h = 10 | a/h = 20 | a/h = 50 | ||||
|---|---|---|---|---|---|---|
|
|
Present | Zhu et al. [4] | Present | Zhu et al. [4] | Present | Zhu et al. [4] |
|
|
21.4953 | 21.544 | 32.5463 | 32.686 | 41.7819 | 42.078 |
|
|
28.4093 | 28.613 | 38.9996 | 39.279 | 47.7825 | 48.309 |
|
|
41.2024 | 41.431 | 53.4057 | 54.560 | 62.3669 | 63.755 |
|
|
41.2818 | 42.119 | 69.5133 | 70.149 | 86.1407 | 90.293 |
|
|
45.5711 | 45.796 | 73.3744 | 73.926 | 104.7524 | 106.513 |
|
|
46.9814 | 47.055 | 75.1651 | 78.522 | 108.3582 | 110.055 |
The next comparison study is devoted to the case of a nonsquare plate with a nonsquare cutout. A thin plate with a/h = 100 and CSCS boundary conditions is considered. The length-to-width ratio is equal to a/b = 1.125. The cutout dimensions are the same as those of Liew et al. [43], that is, c/a = 1/3 and d/b = 1/3. The first four frequencies of the plate are obtained and compared with the available data in the literature. It is worth noting that, in this case, the experimental results of Aksu and Ali [47] are also available. A comparison is provided in Table 6. It is seen that the results of our study match well with the available data in the literature.
Table 6:
First four frequency parameters, , for a CSCS, rectangular, isotropic, homogeneous plate with a rectangular cutout with ν = 0.3, c/a = d/b = 1/3, a/b = 9/8 and a/h = 100.
Table 7 presents the fundamental and second symmetric modes of the frequency parameters of a unidirectional, orthotropic plate in a square platform with a centric square cutout. The material properties of the layer are E11 = 140 GPa, E22 = 3.5 GPa, G12 = 0.5 GPa, ν12 = 0.25 and ρ = 4000 kg/m3. The plate is simply supported all around and a cutout size is chosen as c/a = 0.5. The results are provided for various side-to-thickness ratios. A comparison is made between the results of our study with those obtained by Reddy [48] based on the finite elements method and by Ovesy and Fazilati [49] based on the finite strip method. The results are provided in Table 7. It can be seen that the results of our study match well with the available data in the literature, which proves the correctness of the formulation and solution method of the present research.
Table 7:
Fundamental and second symmetric mode frequency parameters, , for a SSSS, square, unidirectional, orthotropic plate with a square cutout with c/a = d/b = 1/2 and various a/h ratios.
|
|
|
|||||
|---|---|---|---|---|---|---|
| h/a | Reddy [48] | Ovesy and Fazilati [49] | Present | Reddy [48] | Ovesy and Fazilati [49] | Present |
| 0.010 | 51.232 | 51.608 | 51.4407 | 112.220 | 111.399 | 112.8712 |
| 0.040 | 48.907 | 49.049 | 49.0386 | 103.430 | 102.478 | 103.4018 |
| 0.050 | 47.934 | 47.975 | 47.9682 | 100.100 | 99.129 | 99.8877 |
| 0.100 | 42.693 | 42.108 | 42.0505 | 83.451 | 82.654 | 82.4266 |
| 0.200 | 34.069 | 32.416 | 32.1979 | 59.074 | 59.071 | 60.7709 |
Parametric studies
After validating the formulation and proposed method of the present research, the parametric studies are provided in this section. In this section, the frequency parameter is defined as , where Dm is the flexural rigidity of a plate made from the polymeric matrix.
Tables 8–11 present the first five frequencies of CNTRC plates in a square shape and side-to-thickness ratio of a/h = 20. Table 8, Table 9, Table 10 and Table 11 are associated with CCCC, CFFF, SSSS and CFCF plates, respectively. The volume fraction of CNTs is chosen as = 0.17. In each case, the frequencies are provided for three different perforation sizes and four different graded patterns of CNTs. It is seen that, similar to the case of plates without a cutout, in plates with a hole, FG-X also has the highest fundamental frequency and FG-O has the lowest. The influence of hole size on fundamental frequency is not monotonic. For instance, in CCCC plates, the fundamental frequency of a plate increases when the hole size increases from c/a = 0.1 to 0.3 and 0.5. This conclusion is qualitatively compatible with the results of Malekzadeh et al. [45] for CCCC FGM plates. For SSSS and CFFF plates, on the other hand, the trend is the inverse and the fundamental frequency of a plate decreases when the hole size increases from c/a = 0.1 to 0.3 and 0.5. The results presented in Tables 8–11 contain both the flexural and extensional as well as coupled (in FG-V type) vibrational modes. As seen from Table 10, the fourth and fifth frequencies of SSSS plates without a cutout or with a cutout size of c/a = 0.1 and 0.3 are the same. These frequencies are in-plane modes and, due to the symmetry of geometry and boundary conditions, they are equal. It is seen that the in-plane frequencies of FG-X and FG-O plates are equal.
Table 8:
First five natural frequency parameters for square FG-CNTRC CCCC plates with a centric cutout. Geometrical characteristics of the plate are a/b = 1, h/a = 0.05 and various c/a ratios. The volume fraction of CNTs is set equal to = 0.17.
| c/a | Type |
|
|
|
|
|
|---|---|---|---|---|---|---|
| 0.0 | UD | 104.7581 | 127.4624 | 177.3348 | 216.4439 | 229.8165 |
| FG-X | 112.9857 | 136.1313 | 187.5684 | 228.1375 | 241.8078 | |
| FG-O | 90.1519 | 114.9774 | 166.5357 | 195.1187 | 209.9151 | |
| FG-V | 97.1637 | 122.2427 | 175.0384 | 205.6517 | 220.5951 | |
| 0.1 | UD | 105.4667 | 127.4527 | 178.2958 | 210.3946 | 229.2000 |
| FG-X | 114.0739 | 136.1672 | 188.9056 | 221.1219 | 241.2009 | |
| FG-O | 90.3317 | 114.9383 | 167.1189 | 190.7122 | 209.3028 | |
| FG-V | 97.5556 | 122.2235 | 175.8912 | 200.6315 | 219.9939 | |
| 0.3 | UD | 120.4439 | 126.9656 | 169.8070 | 188.2571 | 218.9324 |
| FG-X | 130.6054 | 136.3973 | 181.1849 | 199.9691 | 230.5113 | |
| FG-O | 102.7080 | 112.4737 | 150.9616 | 174.3439 | 199.9412 | |
| FG-V | 111.1976 | 120.2882 | 160.6058 | 183.8592 | 210.3512 | |
| 0.5 | UD | 144.3419 | 145.0951 | 220.7844 | 229.0503 | 231.6397 |
| FG-X | 155.3892 | 156.2246 | 233.7825 | 242.7781 | 244.6759 | |
| FG-O | 129.1618 | 129.9906 | 196.1895 | 205.0887 | 209.8574 | |
| FG-V | 137.8894 | 138.7569 | 208.3156 | 208.3156 | 217.4388 | |
Table 9:
First five natural frequency parameters for square, FG-CNTRC, CFFF plates with a centric cutout. Geometrical characteristics of the plate are a/b = 1, h/a = 0.05 with various c/a ratios. The volume fraction of CNTs is set equal to = 0.17.
| c/a | Type |
|
|
|
|
|
|---|---|---|---|---|---|---|
| 0.0 | UD | 22.7727 | 24.3214 | 40.0851 | 69.2495 | 83.6431 |
| FG-X | 27.0842 | 28.4568 | 44.0066 | 69.7239 | 89.4504 | |
| FG-O | 16.7435 | 18.7782 | 36.1389 | 69.7239 | 79.6264 | |
| FG-V | 19.1381 | 21.0721 | 38.7339 | 69.6796 | 84.0389 | |
| 0.1 | UD | 22.6504 | 24.2757 | 40.0027 | 68.9550 | 83.8138 |
| FG-X | 26.9308 | 28.4058 | 43.8532 | 69.4269 | 89.3451 | |
| FG-O | 16.6641 | 18.7287 | 36.0570 | 69.4269 | 79.5320 | |
| FG-V | 19.0430 | 21.0212 | 38.6399 | 69.3808 | 83.9355 | |
| 0.3 | UD | 20.4172 | 24.0224 | 37.9453 | 65.3384 | 81.1811 |
| FG-X | 24.0635 | 28.1470 | 41.3325 | 65.7754 | 86.5017 | |
| FG-O | 15.2671 | 18.4600 | 34.5625 | 65.7754 | 76.7925 | |
| FG-V | 17.3638 | 20.7497 | 36.9148 | 65.6852 | 81.0431 | |
| 0.5 | UD | 16.9516 | 23.0500 | 34.9990 | 55.9159 | 75.0937 |
| FG-X | 19.6883 | 27.0578 | 38.2949 | 56.2537 | 79.9457 | |
| FG-O | 12.9576 | 17.6252 | 31.7571 | 56.2537 | 70.7251 | |
| FG-V | 14.6594 | 19.8497 | 33.9178 | 56.0921 | 74.7579 | |
Table 10:
First five natural frequency parameters for square, FG-CNTRC, SSSS plates with a centric cutout. Geometrical characteristics of the plate are a/b = 1, h/a = 0.05 with various c/a ratios. The volume fraction of CNTs is set equal to 0.17.
| c/a | Type |
|
|
|
|
|
|---|---|---|---|---|---|---|
| 0.0 | UD | 63.2598 | 83.2741 | 132.0746 | 143.7036 | 143.7036 |
| FG-X | 72.8708 | 92.2430 | 141.7590 | 144.7344 | 144.7344 | |
| FG-O | 49.4292 | 72.4990 | 123.2571 | 144.7344 | 144.7344 | |
| FG-V | 55.2524 | 78.2905 | 130.3768 | 144.7268 | 144.7268 | |
| 0.1 | UD | 62.8020 | 83.1849 | 131.8828 | 144.8261 | 144.8261 |
| FG-X | 72.4414 | 92.1454 | 141.5884 | 145.8609 | 145.8609 | |
| FG-O | 49.0286 | 72.4102 | 123.0916 | 145.8609 | 145.8609 | |
| FG-V | 54.8235 | 78.1925 | 130.2147 | 145.8510 | 145.8510 | |
| 0.3 | UD | 52.8233 | 78.3506 | 111.6736 | 130.6302 | 154.9683 |
| FG-X | 60.5716 | 87.1986 | 119.1929 | 139.3437 | 156.0783 | |
| FG-O | 41.9863 | 67.4468 | 100.7698 | 123.2779 | 156.0783 | |
| FG-V | 46.7420 | 73.0816 | 107.2829 | 129.9159 | 156.0612 | |
| 0.5 | UD | 49.7695 | 72.2115 | 75.6430 | 110.4459 | 153.9671 |
| FG-X | 56.2066 | 80.5715 | 80.8909 | 118.0424 | 165.6159 | |
| FG-O | 40.9160 | 31.2728 | 69.6564 | 103.1278 | 136.3056 | |
| FG-V | 45.0900 | 66.7584 | 73.9966 | 108.6995 | 146.1801 | |
Table 11:
First five natural frequency parameters for square, FG-CNTRC, CFCF plates with a centric cutout. Geometrical characteristics of the plate are a/b = 1, h/a = 0.05 with various c/a ratios. The volume fraction of CNTs is set equal to 0.17.
| c/a | Type |
|
|
|
|
|
|---|---|---|---|---|---|---|
| 0.0 | UD | 100.1209 | 100.5478 | 106.0262 | 130.1245 | 142.0229 |
| FG-X | 108.3648 | 108.7314 | 114.1163 | 138.8282 | 143.0241 | |
| FG-O | 84.7084 | 85.3698 | 92.0274 | 118.2125 | 143.0241 | |
| FG-V | 91.7731 | 92.3623 | 98.8950 | 125.5211 | 142.9107 | |
| 0.1 | UD | 100.2534 | 100.3429 | 106.3842 | 129.9112 | 143.1875 |
| FG-X | 108.5295 | 108.6060 | 114.7279 | 138.6133 | 144.1970 | |
| FG-O | 84.6851 | 85.1671 | 92.0179 | 117.9871 | 144.1970 | |
| FG-V | 91.8120 | 92.1557 | 99.0190 | 125.2861 | 144.0832 | |
| 0.3 | UD | 100.7600 | 101.2200 | 118.8467 | 128.0103 | 153.1897 |
| FG-X | 108.9985 | 109.4736 | 128.8350 | 137.2623 | 154.2720 | |
| FG-O | 85.4922 | 85.9562 | 101.4103 | 114.2352 | 151.0984 | |
| FG-V | 92.5250 | 93.0347 | 109.7041 | 121.8601 | 154.1448 | |
| 0.5 | UD | 101.6312 | 101.6706 | 134.2600 | 134.9668 | 164.4286 |
| FG-X | 109.8563 | 109.9006 | 144.0598 | 144.7920 | 165.5952 | |
| FG-O | 86.8830 | 86.5131 | 118.6095 | 119.3833 | 165.5945 | |
| FG-V | 93.5251 | 93.5551 | 126.8153 | 127.6207 | 165.3665 | |
Table 12 presents the first five frequencies (including both in-plane and out-of-plane) of square plates made of FG-CNTRC with centric cutouts of various sizes. The side-to-thickness ratio is set equal to a/h = 20 and the plate is clamped all around. Numerical results are given for three different volume fractions of CNTs and four different graded patterns of CNTs. Similar to the case of plates without a cutout, an increase in the CNT volume fraction yields a higher natural frequency of the plate. The plates with an FG-X pattern of CNTs have higher frequencies in comparison to UD, FG-V and FG-O plates.
Table 12: First five natural frequency parameters for square, FG-CNTRC, CCCC plates with a centric cutout. The geometrical characteristics of the plate are a/b = 1, h/a = 0.05 and c/a = 0.5.
| c/a |
|
Type |
|
|
|
|
|
|---|---|---|---|---|---|---|---|
| 0.1 | 0.12 | UD | 83.9188 | 100.3679 | 139.1968 | 165.6225 | 180.1856 |
| FG-X | 89.8427 | 105.9079 | 145.2992 | 172.7141 | 187.9588 | ||
| FG-O | 72.7097 | 91.3377 | 131.5790 | 151.3920 | 165.3920 | ||
| FG-V | 78.0171 | 96.2557 | 136.8848 | 158.4278 | 173.2206 | ||
| 0.17 | UD | 105.4667 | 127.4527 | 178.2958 | 210.3946 | 229.2000 | |
| FG-X | 114.0739 | 136.1672 | 188.9056 | 221.1219 | 241.2009 | ||
| FG-O | 90.3317 | 114.9383 | 167.1189 | 190.7122 | 209.3028 | ||
| FG-V | 97.5556 | 122.2235 | 175.8912 | 200.6315 | 219.9939 | ||
| 0.28 | UD | 117.9367 | 139.0787 | 190.6561 | 229.2992 | 249.0083 | |
| FG-X | 128.1334 | 152.0944 | 210.3997 | 243.4859 | 266.0974 | ||
| FG-O | 103.9972 | 126.0241 | 176.2058 | 214.6312 | 232.7102 | ||
| FG-V | 111.7471 | 135.8179 | 190.8244 | 224.2330 | 244.4012 | ||
| 0.3 | 0.12 | UD | 95.8721 | 100.3370 | 134.1470 | 147.7287 | 172.0447 |
| FG-X | 102.8278 | 106.5212 | 141.7684 | 154.5267 | 179.4637 | ||
| FG-O | 82.7712 | 89.7543 | 120.3341 | 137.5941 | 158.4212 | ||
| FG-V | 89.0013 | 95.2007 | 127.2195 | 143.6480 | 165.5769 | ||
| 0.17 | UD | 120.4439 | 126.9656 | 169.8070 | 188.2571 | 218.9324 | |
| FG-X | 130.6054 | 136.3973 | 181.1849 | 199.9691 | 230.5113 | ||
| FG-O | 102.7080 | 112.4737 | 150.9616 | 174.3439 | 199.9412 | ||
| FG-V | 111.1976 | 120.2882 | 160.6058 | 183.8592 | 210.3512 | ||
| 0.28 | UD | 134.7884 | 139.7667 | 186.8796 | 202.9367 | 237.6707 | |
| FG-X | 147.0185 | 152.8559 | 201.8094 | 222.8837 | 254.4027 | ||
| FG-O | 118.3189 | 125.0040 | 169.6503 | 186.3970 | 221.8681 | ||
| FG-V | 127.5548 | 135.0123 | 180.5800 | 201.1201 | 233.5064 | ||
| 0.5 | 0.12 | UD | 114.3763 | 114.9769 | 174.3637 | 180.8571 | 182.4758 |
| FG-X | 121.0992 | 121.7038 | 182.9347 | 189.6084 | 190.7261 | ||
| FG-O | 102.9381 | 103.5831 | 156.5728 | 163.3712 | 166.6608 | ||
| FG-V | 108.9502 | 109.6062 | 165.2573 | 172.0949 | 174.7810 | ||
| 0.17 | UD | 144.3419 | 145.0951 | 220.7844 | 229.0503 | 231.6397 | |
| FG-X | 155.3892 | 156.2246 | 233.7825 | 242.7781 | 244.6759 | ||
| FG-O | 129.1618 | 129.9906 | 196.1895 | 205.0887 | 209.8574 | ||
| FG-V | 137.8894 | 138.7569 | 208.3156 | 208.3156 | 217.4388 | ||
| 0.28 | UD | 158.9989 | 159.7737 | 242.3844 | 251.0307 | 252.5998 | |
| FG-X | 173.8958 | 174.8389 | 258.3101 | 268.3936 | 270.2030 | ||
| FG-O | 143.1568 | 143.9204 | 223.0877 | 231.1761 | 234.5069 | ||
| FG-V | 154.2322 | 155.1098 | 234.8549 | 244.0462 | 247.0420 | ||
Conclusion
The natural frequencies of carbon-nanotube-reinforced, composite laminated plates with a rectangular hole in the center was analyzed in this research. The properties of the plate were obtained according to a modified rule of mixtures, which includes the efficiency parameters to account for the size-dependent characteristics of the nanocomposite. The distribution of CNTs across the plate thickness was both uniform or functionally graded. An energy-based Ritz formulation was constructed to obtain the frequencies of the plate. The basis shape functions were obtained using the Chebyshev polynomials, suitable for arbitrary in-plane and out-of-plane boundary conditions on the exterior and the cutout is assumed to be free. After performing comparison studies for isotropic and unidirectional plates with a centric cutout, the parametric studies were given for plates both with and without a cutout. It is shown that, similar to FG-CNTRC plates without a cutout, increasing the CNT volume fraction results in higher frequencies of the plate with a cutout. Furthermore, FG-X plates have a higher natural frequency in comparison to the other three patterns of CNTs. It was also demonstrated that the variation of fundamental frequency of a perforated plate with respect to the hole size is not monotonic and is dependent on the boundary conditions.
References
-
Kwon, H.; Bradbury, C. R.; Leparoux, M. Adv. Eng. Mater. 2011, 13, 325–329. doi:10.1002/adem.201000251
Return to citation in text: [1] -
Liew, K. M.; Lei, Z. X.; Zhang, L. W. Compos. Struct. 2015, 120, 90–97. doi:10.1016/j.compstruct.2014.09.041
Return to citation in text: [1] -
Shen, H.-S. Compos. Struct. 2009, 91, 9–19. doi:10.1016/j.compstruct.2009.04.026
Return to citation in text: [1] [2] [3] -
Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] -
Zhang, L. W.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2015, 122, 172–183. doi:10.1016/j.compstruct.2014.11.070
Return to citation in text: [1] [2] -
Zhang, L. W.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2015, 120, 189–199. doi:10.1016/j.compstruct.2014.10.009
Return to citation in text: [1] [2] -
Zhang, L. W.; Lei, Z. X.; Liew, K. M.; Yu, J. L. Compos. Struct. 2014, 111, 205–212. doi:10.1016/j.compstruct.2013.12.035
Return to citation in text: [1] [2] -
Zhang, L. W.; Lei, Z. X.; Liew, K. M. Appl. Math. Comput. 2015, 256, 488–504. doi:10.1016/j.amc.2015.01.066
Return to citation in text: [1] -
Lei, Z. X.; Zhang, L. W.; Liew, K. M. Compos. Struct. 2015, 127, 245–259. doi:10.1016/j.compstruct.2015.03.019
Return to citation in text: [1] -
Malekzadeh, P.; Zarei, A. R. Thin-Walled Struct. 2014, 82, 221–232. doi:10.1016/j.tws.2014.04.016
Return to citation in text: [1] -
Malekzadeh, P.; Heydarpour, Y. Meccanica 2015, 50, 143–167. doi:10.1007/s11012-014-0061-4
Return to citation in text: [1] -
Natarajan, S.; Haboussi, M.; Manickam, G. Compos. Struct. 2014, 113, 197–207. doi:10.1016/j.compstruct.2014.03.007
Return to citation in text: [1] -
Wang, Z.-X.; Shen, H.-S. Comput. Mater. Sci. 2011, 50, 2319–2330. doi:10.1016/j.commatsci.2011.03.005
Return to citation in text: [1] [2] -
Wang, Z.-X.; Shen, H.-S. Composites, Part B 2012, 43, 411–421. doi:10.1016/j.compositesb.2011.04.040
Return to citation in text: [1] [2] -
Wang, Z.-X.; Shen, H.-S. Nonlinear Dyn. 2012, 70, 735–754. doi:10.1007/s11071-012-0491-2
Return to citation in text: [1] -
Lei, Z. X.; Zhang, L. W.; Liew, K. M. Int. J. Mech. Sci. 2015, 99, 208–217. doi:10.1016/j.ijmecsci.2015.05.014
Return to citation in text: [1] -
Lei, Z. X.; Zhang, L. W.; Liew, K. M.; Yu, J. M. Compos. Struct. 2014, 113, 328–338. doi:10.1016/j.compstruct.2014.03.035
Return to citation in text: [1] -
Zhang, L. W.; Song, Z. G.; Liew, K. M. Compos. Struct. 2015, 134, 989–1003. doi:10.1016/j.compstruct.2015.08.138
Return to citation in text: [1] -
Zhang, L. W.; Liew, K. M. Compos. Struct. 2015, 132, 974–983. doi:10.1016/j.compstruct.2015.07.017
Return to citation in text: [1] -
Zhang, L. W.; Song, Z. G.; Liew, K. M. Compos. Struct. 2015, 128, 165–175. doi:10.1016/j.compstruct.2015.03.011
Return to citation in text: [1] -
Zhang, L. W.; Cui, W. C.; Liew, K. M. Int. J. Mech. Sci. 2015, 103, 9–21. doi:10.1016/j.ijmecsci.2015.08.021
Return to citation in text: [1] -
Zhang, L. W.; Liew, K. M. Comput. Methods Appl. Mech. Eng. 2015, 295, 219–239. doi:10.1016/j.cma.2015.07.006
Return to citation in text: [1] -
Zhang, L. W.; Lei, Z. X.; Liew, K. M. Composites, Part B 2015, 75, 36–46. doi:10.1016/j.compositesb.2015.01.033
Return to citation in text: [1] -
Lei, Z. X.; Zhang, L. W.; Liew, K. M. Composites, Part B 2016, 84, 211–221. doi:10.1016/j.compositesb.2015.08.081
Return to citation in text: [1] -
Zhang, L. W.; Liew, K. M.; Reddy, J. N. Comput. Methods Appl. Mech. Eng. 2016, 298, 1–28. doi:10.1016/j.cma.2015.09.016
Return to citation in text: [1] -
Shi, D.-L.; Feng, X.-Q.; Huang, Y. Y.; Hwang, K.-C.; Gao, H. J. Eng. Mater. Technol. 2004, 126, 250–257. doi:10.1115/1.1751182
Return to citation in text: [1] -
Fidelus, J. D.; Wiesel, E.; Gojny, F. H.; Schulte, K.; Wagner, H. D. Composites, Part A 2005, 36, 1555–1561. doi:10.1016/j.compositesa.2005.02.006
Return to citation in text: [1] -
Shen, H.-S. Compos. Struct. 2011, 93, 2096–2108. doi:10.1016/j.compstruct.2011.02.011
Return to citation in text: [1] [2] [3] [4] [5] [6] -
Jam, J. E.; Kiani, Y. Compos. Struct. 2015, 125, 586–595. doi:10.1016/j.compstruct.2015.02.052
Return to citation in text: [1] [2] [3] [4] -
Jam, J. E.; Kiani, Y. Compos. Struct. 2015, 132, 35–43. doi:10.1016/j.compstruct.2015.04.045
Return to citation in text: [1] [2] -
Mirzaei, M.; Kiani, Y. Compos. Struct. 2015, 134, 1004–1013. doi:10.1016/j.compstruct.2015.09.003
Return to citation in text: [1] [2] -
Mirzaei, M.; Kiani, Y. Aerosp. Sci. Technol. 2015, 47, 42–53. doi:10.1016/j.ast.2015.09.011
Return to citation in text: [1] [2] -
Mirzaei, M.; Kiani, Y. Compos. Struct. 2016, 142, 45–56. doi:10.1016/j.compstruct.2015.12.071
Return to citation in text: [1] -
Mirzaei, M.; Kiani, Y. Meccanica 2016, 1–17. doi:10.1007/s11012-015-0348-0
Return to citation in text: [1] -
Reddy, J. N. Mechanics of Laminated Composite Plates and Shells, Theory and Application; CRC Press: Boca Raton, FL, U.S.A., 2003.
Return to citation in text: [1] [2] -
Zhang, L. W.; Zhu, P.; Liew, K. M. Compos. Struct. 2014, 108, 472–492. doi:10.1016/j.compstruct.2013.09.043
Return to citation in text: [1] -
Zhu, P.; Zhang, L. W.; Liew, K. M. Compos. Struct. 2014, 107, 298–314. doi:10.1016/j.compstruct.2013.08.001
Return to citation in text: [1] -
Zhang, L. W.; Li, D. M.; Liew, K. M. Eng. Anal. Boundary Elem. 2015, 54, 39–46. doi:10.1016/j.enganabound.2015.01.007
Return to citation in text: [1] -
Zhang, L. W.; Huang, D.; Liew, K. M. Comput. Methods Appl. Mech. Eng. 2015, 297, 116–139. doi:10.1016/j.cma.2015.08.018
Return to citation in text: [1] -
Shen, H.-S.; Xiang, Y. Eng. Struct. 2013, 56, 698–708. doi:10.1016/j.engstruct.2013.06.002
Return to citation in text: [1] -
Han, Y.; Elliott, J. Comput. Mater. Sci. 2007, 39, 315–323. doi:10.1016/j.commatsci.2006.06.011
Return to citation in text: [1] [2] -
Wang, C. Y.; Zhang, L. C. Nanotechnology 2008, 19, 075705. doi:10.1088/0957-4484/19/7/075705
Return to citation in text: [1] -
Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] -
Lam, K. Y.; Hung, K. C.; Chow, S. T. Appl. Acoustics 1989, 28, 49–60. doi:10.1016/0003-682X(89)90030-3
Return to citation in text: [1] [2] [3] [4] [5] -
Malekzadeh, P.; Bahranifard, F.; Ziaee, S. Compos. Struct. 2013, 105, 1–13. doi:10.1016/j.compstruct.2013.05.005
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] [8] -
Mundkur, G.; Bhat, R. B.; Neriya, S. J. Sound Vib. 1994, 176, 136–144. doi:10.1006/jsvi.1994.1364
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] -
Aksu, G.; Ali, R. J. Sound Vib. 1976, 44, 147–158. doi:10.1016/0022-460X(76)90713-6
Return to citation in text: [1] [2] [3] -
Reddy, J. N. J. Sound Vib. 1982, 83, 1–10. doi:10.1016/S0022-460X(82)80071-0
Return to citation in text: [1] [2] [3] -
Ovesy, H. R.; Fazilati, J. Compos. Struct. 2012, 94, 1250–1258. doi:10.1016/j.compstruct.2011.11.009
Return to citation in text: [1] [2] [3]
| 13. | Wang, Z.-X.; Shen, H.-S. Comput. Mater. Sci. 2011, 50, 2319–2330. doi:10.1016/j.commatsci.2011.03.005 |
| 14. | Wang, Z.-X.; Shen, H.-S. Composites, Part B 2012, 43, 411–421. doi:10.1016/j.compositesb.2011.04.040 |
| 35. | Reddy, J. N. Mechanics of Laminated Composite Plates and Shells, Theory and Application; CRC Press: Boca Raton, FL, U.S.A., 2003. |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 29. | Jam, J. E.; Kiani, Y. Compos. Struct. 2015, 125, 586–595. doi:10.1016/j.compstruct.2015.02.052 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 42. | Wang, C. Y.; Zhang, L. C. Nanotechnology 2008, 19, 075705. doi:10.1088/0957-4484/19/7/075705 |
| 28. | Shen, H.-S. Compos. Struct. 2011, 93, 2096–2108. doi:10.1016/j.compstruct.2011.02.011 |
| 28. | Shen, H.-S. Compos. Struct. 2011, 93, 2096–2108. doi:10.1016/j.compstruct.2011.02.011 |
| 44. | Lam, K. Y.; Hung, K. C.; Chow, S. T. Appl. Acoustics 1989, 28, 49–60. doi:10.1016/0003-682X(89)90030-3 |
| 41. | Han, Y.; Elliott, J. Comput. Mater. Sci. 2007, 39, 315–323. doi:10.1016/j.commatsci.2006.06.011 |
| 40. | Shen, H.-S.; Xiang, Y. Eng. Struct. 2013, 56, 698–708. doi:10.1016/j.engstruct.2013.06.002 |
| 47. | Aksu, G.; Ali, R. J. Sound Vib. 1976, 44, 147–158. doi:10.1016/0022-460X(76)90713-6 |
| 41. | Han, Y.; Elliott, J. Comput. Mater. Sci. 2007, 39, 315–323. doi:10.1016/j.commatsci.2006.06.011 |
| 47. | Aksu, G.; Ali, R. J. Sound Vib. 1976, 44, 147–158. doi:10.1016/0022-460X(76)90713-6 |
| 35. | Reddy, J. N. Mechanics of Laminated Composite Plates and Shells, Theory and Application; CRC Press: Boca Raton, FL, U.S.A., 2003. |
| 47. | Aksu, G.; Ali, R. J. Sound Vib. 1976, 44, 147–158. doi:10.1016/0022-460X(76)90713-6 |
| 36. | Zhang, L. W.; Zhu, P.; Liew, K. M. Compos. Struct. 2014, 108, 472–492. doi:10.1016/j.compstruct.2013.09.043 |
| 37. | Zhu, P.; Zhang, L. W.; Liew, K. M. Compos. Struct. 2014, 107, 298–314. doi:10.1016/j.compstruct.2013.08.001 |
| 38. | Zhang, L. W.; Li, D. M.; Liew, K. M. Eng. Anal. Boundary Elem. 2015, 54, 39–46. doi:10.1016/j.enganabound.2015.01.007 |
| 39. | Zhang, L. W.; Huang, D.; Liew, K. M. Comput. Methods Appl. Mech. Eng. 2015, 297, 116–139. doi:10.1016/j.cma.2015.08.018 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
| 28. | Shen, H.-S. Compos. Struct. 2011, 93, 2096–2108. doi:10.1016/j.compstruct.2011.02.011 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
| 44. | Lam, K. Y.; Hung, K. C.; Chow, S. T. Appl. Acoustics 1989, 28, 49–60. doi:10.1016/0003-682X(89)90030-3 |
| 49. | Ovesy, H. R.; Fazilati, J. Compos. Struct. 2012, 94, 1250–1258. doi:10.1016/j.compstruct.2011.11.009 |
| 49. | Ovesy, H. R.; Fazilati, J. Compos. Struct. 2012, 94, 1250–1258. doi:10.1016/j.compstruct.2011.11.009 |
| 49. | Ovesy, H. R.; Fazilati, J. Compos. Struct. 2012, 94, 1250–1258. doi:10.1016/j.compstruct.2011.11.009 |
| 45. | Malekzadeh, P.; Bahranifard, F.; Ziaee, S. Compos. Struct. 2013, 105, 1–13. doi:10.1016/j.compstruct.2013.05.005 |
| 46. | Mundkur, G.; Bhat, R. B.; Neriya, S. J. Sound Vib. 1994, 176, 136–144. doi:10.1006/jsvi.1994.1364 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
| 44. | Lam, K. Y.; Hung, K. C.; Chow, S. T. Appl. Acoustics 1989, 28, 49–60. doi:10.1016/0003-682X(89)90030-3 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
| 44. | Lam, K. Y.; Hung, K. C.; Chow, S. T. Appl. Acoustics 1989, 28, 49–60. doi:10.1016/0003-682X(89)90030-3 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
| 45. | Malekzadeh, P.; Bahranifard, F.; Ziaee, S. Compos. Struct. 2013, 105, 1–13. doi:10.1016/j.compstruct.2013.05.005 |
| 44. | Lam, K. Y.; Hung, K. C.; Chow, S. T. Appl. Acoustics 1989, 28, 49–60. doi:10.1016/0003-682X(89)90030-3 |
| 46. | Mundkur, G.; Bhat, R. B.; Neriya, S. J. Sound Vib. 1994, 176, 136–144. doi:10.1006/jsvi.1994.1364 |
| 45. | Malekzadeh, P.; Bahranifard, F.; Ziaee, S. Compos. Struct. 2013, 105, 1–13. doi:10.1016/j.compstruct.2013.05.005 |
| 45. | Malekzadeh, P.; Bahranifard, F.; Ziaee, S. Compos. Struct. 2013, 105, 1–13. doi:10.1016/j.compstruct.2013.05.005 |
| 1. | Kwon, H.; Bradbury, C. R.; Leparoux, M. Adv. Eng. Mater. 2011, 13, 325–329. doi:10.1002/adem.201000251 |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 14. | Wang, Z.-X.; Shen, H.-S. Composites, Part B 2012, 43, 411–421. doi:10.1016/j.compositesb.2011.04.040 |
| 46. | Mundkur, G.; Bhat, R. B.; Neriya, S. J. Sound Vib. 1994, 176, 136–144. doi:10.1006/jsvi.1994.1364 |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 15. | Wang, Z.-X.; Shen, H.-S. Nonlinear Dyn. 2012, 70, 735–754. doi:10.1007/s11071-012-0491-2 |
| 3. | Shen, H.-S. Compos. Struct. 2009, 91, 9–19. doi:10.1016/j.compstruct.2009.04.026 |
| 12. | Natarajan, S.; Haboussi, M.; Manickam, G. Compos. Struct. 2014, 113, 197–207. doi:10.1016/j.compstruct.2014.03.007 |
| 46. | Mundkur, G.; Bhat, R. B.; Neriya, S. J. Sound Vib. 1994, 176, 136–144. doi:10.1006/jsvi.1994.1364 |
| 2. | Liew, K. M.; Lei, Z. X.; Zhang, L. W. Compos. Struct. 2015, 120, 90–97. doi:10.1016/j.compstruct.2014.09.041 |
| 13. | Wang, Z.-X.; Shen, H.-S. Comput. Mater. Sci. 2011, 50, 2319–2330. doi:10.1016/j.commatsci.2011.03.005 |
| 45. | Malekzadeh, P.; Bahranifard, F.; Ziaee, S. Compos. Struct. 2013, 105, 1–13. doi:10.1016/j.compstruct.2013.05.005 |
| 8. | Zhang, L. W.; Lei, Z. X.; Liew, K. M. Appl. Math. Comput. 2015, 256, 488–504. doi:10.1016/j.amc.2015.01.066 |
| 10. | Malekzadeh, P.; Zarei, A. R. Thin-Walled Struct. 2014, 82, 221–232. doi:10.1016/j.tws.2014.04.016 |
| 46. | Mundkur, G.; Bhat, R. B.; Neriya, S. J. Sound Vib. 1994, 176, 136–144. doi:10.1006/jsvi.1994.1364 |
| 7. | Zhang, L. W.; Lei, Z. X.; Liew, K. M.; Yu, J. L. Compos. Struct. 2014, 111, 205–212. doi:10.1016/j.compstruct.2013.12.035 |
| 11. | Malekzadeh, P.; Heydarpour, Y. Meccanica 2015, 50, 143–167. doi:10.1007/s11012-014-0061-4 |
| 45. | Malekzadeh, P.; Bahranifard, F.; Ziaee, S. Compos. Struct. 2013, 105, 1–13. doi:10.1016/j.compstruct.2013.05.005 |
| 6. | Zhang, L. W.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2015, 120, 189–199. doi:10.1016/j.compstruct.2014.10.009 |
| 46. | Mundkur, G.; Bhat, R. B.; Neriya, S. J. Sound Vib. 1994, 176, 136–144. doi:10.1006/jsvi.1994.1364 |
| 5. | Zhang, L. W.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2015, 122, 172–183. doi:10.1016/j.compstruct.2014.11.070 |
| 9. | Lei, Z. X.; Zhang, L. W.; Liew, K. M. Compos. Struct. 2015, 127, 245–259. doi:10.1016/j.compstruct.2015.03.019 |
| 45. | Malekzadeh, P.; Bahranifard, F.; Ziaee, S. Compos. Struct. 2013, 105, 1–13. doi:10.1016/j.compstruct.2013.05.005 |
| 3. | Shen, H.-S. Compos. Struct. 2009, 91, 9–19. doi:10.1016/j.compstruct.2009.04.026 |
| 16. | Lei, Z. X.; Zhang, L. W.; Liew, K. M. Int. J. Mech. Sci. 2015, 99, 208–217. doi:10.1016/j.ijmecsci.2015.05.014 |
| 17. | Lei, Z. X.; Zhang, L. W.; Liew, K. M.; Yu, J. M. Compos. Struct. 2014, 113, 328–338. doi:10.1016/j.compstruct.2014.03.035 |
| 18. | Zhang, L. W.; Song, Z. G.; Liew, K. M. Compos. Struct. 2015, 134, 989–1003. doi:10.1016/j.compstruct.2015.08.138 |
| 19. | Zhang, L. W.; Liew, K. M. Compos. Struct. 2015, 132, 974–983. doi:10.1016/j.compstruct.2015.07.017 |
| 20. | Zhang, L. W.; Song, Z. G.; Liew, K. M. Compos. Struct. 2015, 128, 165–175. doi:10.1016/j.compstruct.2015.03.011 |
| 21. | Zhang, L. W.; Cui, W. C.; Liew, K. M. Int. J. Mech. Sci. 2015, 103, 9–21. doi:10.1016/j.ijmecsci.2015.08.021 |
| 22. | Zhang, L. W.; Liew, K. M. Comput. Methods Appl. Mech. Eng. 2015, 295, 219–239. doi:10.1016/j.cma.2015.07.006 |
| 23. | Zhang, L. W.; Lei, Z. X.; Liew, K. M. Composites, Part B 2015, 75, 36–46. doi:10.1016/j.compositesb.2015.01.033 |
| 24. | Lei, Z. X.; Zhang, L. W.; Liew, K. M. Composites, Part B 2016, 84, 211–221. doi:10.1016/j.compositesb.2015.08.081 |
| 25. | Zhang, L. W.; Liew, K. M.; Reddy, J. N. Comput. Methods Appl. Mech. Eng. 2016, 298, 1–28. doi:10.1016/j.cma.2015.09.016 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
| 45. | Malekzadeh, P.; Bahranifard, F.; Ziaee, S. Compos. Struct. 2013, 105, 1–13. doi:10.1016/j.compstruct.2013.05.005 |
| 46. | Mundkur, G.; Bhat, R. B.; Neriya, S. J. Sound Vib. 1994, 176, 136–144. doi:10.1006/jsvi.1994.1364 |
| 28. | Shen, H.-S. Compos. Struct. 2011, 93, 2096–2108. doi:10.1016/j.compstruct.2011.02.011 |
| 29. | Jam, J. E.; Kiani, Y. Compos. Struct. 2015, 125, 586–595. doi:10.1016/j.compstruct.2015.02.052 |
| 28. | Shen, H.-S. Compos. Struct. 2011, 93, 2096–2108. doi:10.1016/j.compstruct.2011.02.011 |
| 29. | Jam, J. E.; Kiani, Y. Compos. Struct. 2015, 125, 586–595. doi:10.1016/j.compstruct.2015.02.052 |
| 30. | Jam, J. E.; Kiani, Y. Compos. Struct. 2015, 132, 35–43. doi:10.1016/j.compstruct.2015.04.045 |
| 31. | Mirzaei, M.; Kiani, Y. Compos. Struct. 2015, 134, 1004–1013. doi:10.1016/j.compstruct.2015.09.003 |
| 32. | Mirzaei, M.; Kiani, Y. Aerosp. Sci. Technol. 2015, 47, 42–53. doi:10.1016/j.ast.2015.09.011 |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 28. | Shen, H.-S. Compos. Struct. 2011, 93, 2096–2108. doi:10.1016/j.compstruct.2011.02.011 |
| 29. | Jam, J. E.; Kiani, Y. Compos. Struct. 2015, 125, 586–595. doi:10.1016/j.compstruct.2015.02.052 |
| 30. | Jam, J. E.; Kiani, Y. Compos. Struct. 2015, 132, 35–43. doi:10.1016/j.compstruct.2015.04.045 |
| 31. | Mirzaei, M.; Kiani, Y. Compos. Struct. 2015, 134, 1004–1013. doi:10.1016/j.compstruct.2015.09.003 |
| 32. | Mirzaei, M.; Kiani, Y. Aerosp. Sci. Technol. 2015, 47, 42–53. doi:10.1016/j.ast.2015.09.011 |
| 33. | Mirzaei, M.; Kiani, Y. Compos. Struct. 2016, 142, 45–56. doi:10.1016/j.compstruct.2015.12.071 |
| 34. | Mirzaei, M.; Kiani, Y. Meccanica 2016, 1–17. doi:10.1007/s11012-015-0348-0 |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 27. | Fidelus, J. D.; Wiesel, E.; Gojny, F. H.; Schulte, K.; Wagner, H. D. Composites, Part A 2005, 36, 1555–1561. doi:10.1016/j.compositesa.2005.02.006 |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 3. | Shen, H.-S. Compos. Struct. 2009, 91, 9–19. doi:10.1016/j.compstruct.2009.04.026 |
| 4. | Zhu, P.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2012, 94, 1450–1460. doi:10.1016/j.compstruct.2011.11.010 |
| 5. | Zhang, L. W.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2015, 122, 172–183. doi:10.1016/j.compstruct.2014.11.070 |
| 6. | Zhang, L. W.; Lei, Z. X.; Liew, K. M. Compos. Struct. 2015, 120, 189–199. doi:10.1016/j.compstruct.2014.10.009 |
| 7. | Zhang, L. W.; Lei, Z. X.; Liew, K. M.; Yu, J. L. Compos. Struct. 2014, 111, 205–212. doi:10.1016/j.compstruct.2013.12.035 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
| 26. | Shi, D.-L.; Feng, X.-Q.; Huang, Y. Y.; Hwang, K.-C.; Gao, H. J. Eng. Mater. Technol. 2004, 126, 250–257. doi:10.1115/1.1751182 |
| 43. | Liew, K. M.; Kitipornchai, S.; Leung, A. Y. T.; Lim, C. W. Int. J. Mech. Sci. 2003, 45, 941–959. doi:10.1016/S0020-7403(03)00109-7 |
© 2016 Mirzaei and Kiani; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Nanotechnology terms and conditions: (http://www.beilstein-journals.org/bjnano)