Abstract
We investigate how the optical gain or loss (characterized by isotropic complex refractive indexes) influence the ideal Kerker scattering of exactly zero backward scattering. It was previously shown that, for non-magnetic homogeneous spheres with incident plane waves, either gain or loss prohibit ideal Kerker scattering, provided that only electric and magnetic multipoles of a specific order are present and contributions from other multipoles can all be made precisely zero. Here we reveal that, when two multipoles of a fixed order are perfectly matched in terms of both phase and magnitude, multipoles of at least the next two orders cannot possibly be tuned to be all precisely zero or even perfectly matched, and consequently cannot directly produce ideal Kerker scattering. Moreover, we further demonstrate that, when multipoles of different orders are simultaneously taken into consideration, loss or gain can serve as helpful rather than harmful contributing factors, for the elimination of backward scattering.
Introduction
The original Kerker scattering of zero backward scattering was first proposed for homogeneous magnetic spheres with equal electric permittivity and magnetic permeability ε = μ [1]. This proposal had not attracted much attention for a long time, mainly due to the scarcity of magnetic materials, especially at the high-frequency spectral regimes. In the past decade, thanks to the explosive developments of metamaterials and metasurfaces, the underlying core concept of optically induced magnetism in non-magnetic structures has invigorated and completely transformed Kerker’s original proposal (see the reviews [2-4]). The fusion of optically induced magnetism with Kerker scattering by high-index materials [5] has rendered new perspectives for photonic studies concerning not only scattering of individual particles or their finite clusters [6,7], but also of extended periodic or aperiodic structures [2-4,8-14]. Moreover, this significantly broadened concept of Kerker scattering has rapidly penetrated into other disciplines of photonics, revealing hidden connections between seemingly unrelated concepts and demonstrations [15-23].
In the original proposal for homogenous spheres with ε = μ, electric and magnetic multipoles of all orders are automatically perfectly matched in terms of both phase and magnitude [24], leading to ideal Kerker scattering of exactly zero backward scattering [1]. Nevertheless, for demonstrations relying on optically induced magnetism with non-magnetic structures (μ = 1), it is rather challenging, if not impossible, to precisely match all multipoles simultaneously, ending up with only significantly suppressed but not exactly zero backward scattering [2-4]. Quite recently, Olmos-Trigo et al. revisited the simplest case of a non-magnetic isotropic and homogeneous sphere with incident plane waves and concluded that: (i) ideal zero backward scattering is achievable only for materials without gain or loss (characterized by real refractive indexes) [25], and (ii) extra gain or loss inhibit such ideal Kerker scattering. Besides the proven feasible perfect matching of electric and magnetic multipoles of one specific fixed order, the validity of the conclusion resides on the additional assumption that magnitudes of multipoles of all other orders can be simultaneously tuned to be perfectly zero. For general discussions of optical properties, such as scattering and absorption cross sections, it is physically legitimate to take into consideration only those dominant contributing multipole terms and drop other minor ones (such as in the widely adopted dipole approximation). While for the investigation into the extreme case of ideal zero backward scattering, those minor multipole terms cannot be simply discarded unless they are exactly zero or also perfectly matched in a similar fashion.
In this work we show that, despite the previously proven fact that multipoles of a fixed order can be perfectly matched in the absence of loss or gain [25], the contributions from multipoles of at least the next two orders cannot be simultaneously tuned to be all zero or perfectly matched. In other words, ideal Kerker scattering of exact zero backward scattering is not directly achievable through matching a pair of multipoles of one specific order only. We further reveal that when multipoles of different orders are all taken into consideration, loss or gain should be employed rather than avoided for the elimination of backward scattering. It is shown that, at the presence of multipoles of various orders, the absence of backward scattering can be obtained through tuning the refractive index on the complex plane, breaking the connection between zero backscattering and helicity conservation.
Results
Formulas and analysis of ideal Kerker scattering
For the scattering of incident linearly polarized plane waves (wavelength λ and angular wavenumber k = 2π/λ) by homogeneous non-magnetic spheres (isotropic refractive index m, radius R, and normalized geometric parameter x = kR), the scattered fields can be expanded into a series of electric and magnetic multipoles of order l (l = 1 corresponds to dipoles). They are characterized, respectively, by the complex Mie coefficients al and bl [26,27]:
where αl and βl are complex phase angles (they are real when m is real). Those phase angles can be obtained through the following relations [26]:
Here the prime ′ denotes first-order derivative with respect to the entire argument in the bracket; Sl(z) = zjl(z) and Cl(z) = −zyl(z) are Riccati–Bessel functions; jl(z) and yl(z) are spherical Bessel functions of the first and second kinds.
With al and bl obtained, the total scattering efficiency can be calculated through [26,27]:
and the ideal Kerker scattering in terms of backward scattering efficiency Qb can be expressed as [26,27]:
Equation 4 has an infinite set of possible solutions, and what is discussed [25] is actually the following very special scenario:
where l0 is an arbitrary natural number and a pair of multipoles of order l0 are perfectly matched as shown in Equation 5. The significant contribution from [25] is to prove rigorously that Equation 5 has a solution only when m is real, meaning that, at the presence of loss or gain, multipoles of the same order cannot be ideally matched. Despite this seminal contribution, there is a problem that in [25] it has not been discussed whether Equation 5 and Equation 6 are really compatible. Such discussions concerning compatibility are vitally important, since Equation 5 will not necessarily lead to ideal Kerker scattering of precise zero backscattering.
Mismatch among multipoles of three successive orders
In this section, we aim to prove that Equation 5 and Equation 6 are not exactly compatible, thus proving that Ideal Kerker scattering of exact zero backward scattering is actually inaccessible through matching multipoles of a specific order only. For all our following discussions, the obviously trivial scenario of m = 1 (we assume that the background medium is air of index 1 throughout our study) or R = 0 is excluded. For another special case of zero index m = 0, the Mie coefficients can be simplified as (as m→0) [26,27]:
where , and
is a spherical Hankel function of the first kind. Since Sl(mx)→0 when m→0, we get a definite al but indefinite bl (L’Hôpital’s rule will not help to make bl definite, since the zero term in the numerator and denominator is the same [28]). So it has been proved that for m = 0, there are no definite scattering properties for ideally monochromatic plane waves. Physical investigations can be implemented only after considering simultaneously the dispersion of the index and the spectrum of the incident waves. Consequently, the zero-index scenario is also excluded in the following analysis.
It has been rigorously proved that the solutions of Equation 5 satisfy either of the following equations:
which do not have a common solution according to the Brauer–Siegel theorem [29,30]. Similarly, to prove that then multipoles of all other orders (l ≠ l0) cannot all be perfectly matched (of which that other multipoles cannot be tuned to be all zero is merely a special scenario), it is more than sufficient to prove that there exists one multipole order l1 (l1 ≠ l0) for which:
Obviously, Equation 10 ensures that , meaning that Equation 6 cannot be simultaneously met.
According to the following recurrence relations of Riccati–Bessel functions [29]:
(i) when and
: According to Equation 12, we obtain
. This together with Equation 11 leads to
. As a result, Equation 10 is satisfied at least for l1 = l0 + 1, securing that
.
(ii) When and
: Also, according to Equation 12, we get
. Nevertheless, according to Equation 11,
if the following conditions can be met:
Nevertheless, following the same logic, extending the multipole matching to the next order l0 + 2 requires:
It is quite obvious that Equation 13 and Equation 14 can not be simultaneously satisfied, that is, mx cannot be both ±(l0 + 1) and ±(l0 + 2), and, thus, multipole mismatch happens at least for l1 = l0 + 2: .
The arguments above, consistent with a recent study [30], confirm that when a multipole of a specific order l0 is perfectly matched in a nontrivial way, Equation 5, the scattering contributions from multipoles of at least the next two successive orders (l0 + 1 and l0 + 2) cannot be simultaneously tuned to be zero or matched. In other words, perfect matching of multipoles of one specific order does not guarantee ideal zero backward scattering.
Effects of gain or loss on ideal Kerker scattering: non-resonant regimes
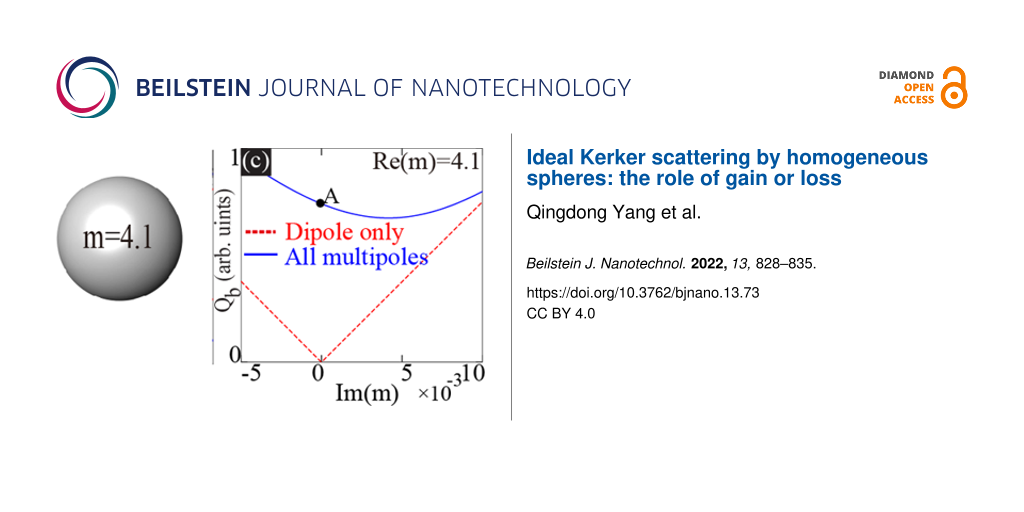
We show in Figure 1 two scenarios where the electric and magnetic dipoles (ED and MD) are perfectly matched in non-resonant spectra regimes. The scattering efficiency spectra (scattering efficiency Qsca as a function of x = kR) for a homogeneous sphere (m = 4.1) are shown in Figure 1a, where both total scattering and the contributions from different multipoles (dipoles and electric and magnetic quadrupoles: EQ and MQ) are included. This is actually the case studied in detail in [25]. The ED and MD are perfectly matched at xA = 0.6684, where . As argued in the last section, at xA, scattering from multipoles of higher orders is not exactly zero (see Figure 1b, which shows an enlarged part of the spectra close to xA in logarithmic scale), though they are much smaller than those of dipoles. For explorations of general properties like scattering and absorption cross sections, it is fine to drop those quadrupole terms and to keep the dipole terms only. Nevertheless, for the study of the extreme case of ideal Kerker scattering, simply discarding those higher-order terms cannot be justified and could even lead to inaccurate conclusions.
![[2190-4286-13-73-1]](/bjnano/content/figures/2190-4286-13-73-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: Scattering spectra (both total scattering and the contributions from different multipoles are included) are shown in (a) and (b) for m = 4.1, and in (d) and (e) for m = 4.29. Here, (b) and (e) are sections of (a) and (b), respectively, which are close to the dipole matching points and enlarged for clarity. For each scenario, there is a indicated point (xA ≈ 0.6684 and xB ≈ 1.0472) where the dipoles are perfectly matched. (c, f) Dependence of Qb on Im(m), at xA with fixed Re(m) = 4.1 and at xB with fixed Re(m) = 4.29, respectively. In (c) and (f), two sets of results are shown, considering only dipoles or all multipoles, respectively.
Figure 1: Scattering spectra (both total scattering and the contributions from different multipoles are inclu...
To verify the claim above, we show in Figure 1c the dependence of the backward scattering efficiency Qb at xA on the imaginary part of refractive index Im(m); the real part of m is fixed at Re(m) = 4.1. Im(m) > 0 and Im(m) < 0 correspond to loss and gain, respectively. Here two sets of spectra are shown, for which either only dipoles or multipoles of all orders are taken into consideration. It is clear from Figure 1c that, when only dipoles are considered, ideal Kerker scattering is achieved when m is real, and any extra loss or gain would inhibit such scattering, as is the major conclusion of [25]. In sharp contrast, when all multipoles are considered, ideal Kerker scattering is not accessible at the perfect matching point of dipoles anymore. Moreover, as shown in Figure 1c, extra loss can be employed to further suppress the backward scattering, serving as a friend rather than a foe for the Kerker scattering. Another scenario of perfect dipole matching at xB = 1.0472 for m = 4.29 is summarized in Figure 1d–f, for which the other perfect matching condition is satisfied, that is S1(mxA) = 0. Here the effects of higher-order multipoles are even more pronounced (see Figure 1f) since the magnitudes of dipoles and higher multipoles are comparable (see Figure 1e.
Effects of gain or loss on ideal Kerker scattering: resonant regimes
In the last section, we discussed only the perfect dipole matching at the non-resonant regimes, where not only the backward scattering is suppressed, but also the overall scattering is small. Such scattering is of very limited significance, since what is widely required in photonics is suppressed backward scattering accompanied by large total scattering [2-4]. In this section, we move to the resonant regimes where the dipoles can be perfectly matched. Two such scenarios are summarized in Figure 2, where the conditions of S1(mxC) = 0 and are satisfied, in Figure 2a–c with xC ≈ 2.7366, m = 5.14, and in Figure 2d–f with xD ≈ 4.4123, and m = 2.83), respectively. In Figure 2, besides the scattering spectra (Figure 2a,d) and dependence of Qb on Im(m) (Figure 2b,e), we show also the two-dimensional (2D) scattering patterns (in the plane parallel to both the incident and polarization directions of the independent plane waves) at the dipole matching points (Figure 2c,f).
![[2190-4286-13-73-2]](/bjnano/content/figures/2190-4286-13-73-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Scattering spectra are shown in (a) for m = 5.14 and in (d) for m = 2.83. For each scenario, there is an indicated point (xC ≈ 2.7366 and xD ≈ 4.4123) where the dipoles are perfectly matched. (b, e) Dependence of Qb on Im(m) at xC with fixed Re(m) = 5.14 and at xD with fixed Re(m) = 2.83, respectively. (c, f) The 2D angular scattering patterns (in the plane parallel to both polarization and incident directions) at xC with m = 5.14 and at xD with m = 2.83, respectively. In (b, c) and (e, f) two sets of results are shown, considering only dipoles or all multipoles, respectively.
Figure 2: Scattering spectra are shown in (a) for m = 5.14 and in (d) for m = 2.83. For each scenario, there ...
As indicated by the scattering spectra, the scattering by the higher-order multipoles is rather strong, which ruins the ideal Kerker scattering (see Figure 2b,e) and makes the overall patterns considering all multipoles (solid lines of Figure 2c,f) contrastingly different from those of matched dipoles only (dashed lines of Figure 2c,f). Similar to what is shown in Figure 1, when all multipoles are considered, extra loss can be employed to further suppress the backward scattering, serving as a constructive rather than a destructive factor for demonstrations of Kerker scattering.
Kerker scattering without multipole matching of any specific order
We have confirmed in the last sections, by both mathematical analysis and numerical calculations, that perfect matching of multipoles of a specific order does not necessarily produce ideal Kerker scattering due to non-negligible higher-order multipoles. Moreover, those higher-order terms would make the extra gain or loss a constructive factor for further suppression of the backward scattering. Now we come back to Equation 4, the solution of which does not really require multipole matching of any specific order (such as those shown in Equation 5 and Equation 6), but can be obtained through fully destructive interferences among multipoles of several orders along the backward direction. Such an effect is also termed as “generalized Kerker effect”, originating from interferences among multipoles of different orders [4,31-34]. Generally speaking, to obtain zero backward scattering with complete destructive interferences among multipoles, at least two multipoles of opposite parities are needed. This could be a pair of multipoles of the same order (such as ED and MD), or two multipoles of different orders (such as ED and EQ, or MD and MQ), or more than two multipoles that are not of the same parity [4,31]. For further confirmation, we show two such scenarios with loss or gain in Figure 3, where Kerker scattering is observed, in Figure 3a,b (xE ≈ 1.9591, m = 1.1875 + 0.1i), and in Figure 3d,e (xF ≈ 1.7492 for m = 1.275 − 4.225i), respectively. Figure 3a,b shows that there is no non-trivial perfect multipole matching (al = bl ≠ 0) at the indicated positions, despite which the Kerker scattering can still be achieved (see Figure 3b,e at xE and xF). Moreover, the dependence of Qb on Im(m) (Figure 3b,e) can confirm that the selected loss or gain is vitally important for such achievement, as a little detuning from them would immediately ruin the Kerker scattering. For both scenarios, it is quite obvious that to fix the index to be real is actually harmful for the suppression of backward scattering.
It has been rigorously proved that n-fold (n ≥ 3) rotation symmetry together with helicity conservation would automatically guarantee ideal Kerker scattering of zero backward scattering [22,35]. For homogenous sphere scattering with incident plane waves, the rotation symmetry is secured (n = ∞) and the helicity conservation requires the multipole matching of all orders. Consequently, Kerker scattering obtained through perfect matching of multipoles at each order are inextricably connected through helicity conservation, as is confirmed in [25]. Nevertheless, we have shown in the last section that Kerker scattering is also achievable without multipole matching of any specific order, for which it is expected that the connection between Kerker scattering and helicity conservation would be broken. To confirm this, we further show the dependence of the helicity conservation factor on Im(m) in Figure 3c,f. Here
is defined as [25,36]:
Here = 1 corresponds to ideal helicity conservation, which means that for incident circularly polarized plane waves, the waves scattered along all directions are also circularly polarized of the same handedness (including the special case of zero scattering) [17,22,37,38]. A comparison between Figure 3c,f and Figure 3b,e can confirm that there is no connection between the Kerker scattering and helicity conservation, since
is far from unity at the indicated Kerker scattering points (
= 0.857,
= 0.2115). In other words, rotation symmetry and helicity conservation lead to zero backward scattering, while rotation symmetry and zero backward scattering does not necessarily imply helicity conservation.
![[2190-4286-13-73-3]](/bjnano/content/figures/2190-4286-13-73-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3:
Scattering spectra are shown in (a) for m = 1.1875 + 0.1i (with loss) and in (d) for m = 1.275 − 4.225i (with gain). For each scenario, there is an indicated point (xE ≈ 1.9591 and xF ≈ 1.7492) where the backward scattering is eliminated, as confirmed in (b) and (e). Dependence of Qb (b, e) and (c, f) on Im(m), at xE with fixed Re(m) = 1.1875 and at xF with fixed Re(m) = 1.275.
Figure 3: Scattering spectra are shown in (a) for m = 1.1875 + 0.1i (with loss) and in (d) for m = 1.275 − 4....
Discussion
There are several significant points worth emphasizing at the end: (i) For numerical demonstrations of perfect multipole matching, we discuss only dipoles while the principles revealed are applicable for multipoles of any order. (ii) In this study, we only discuss Kerker scattering of zero backward scattering (first Kerker scattering). For the second Kerker scattering of zero forward scattering, despite the inevitable involvement of gain materials as required by optical theorem, multipoles of various order rather than a specific order should be taken into considerations simultaneously, as has been implemented in this work. (iii) Is ideal Kerker scattering of exact zero backward scattering achievable, in a rigorously mathematical sense, with homogenous non-magnetic spheres? The answer is: We do not know. It is well known that for arbitrary algebraic equations of order L,
for which L is a finite natural number and cl are complex constant coefficients, the fundamental theorem of algebra secures that there is at least one solution on the complex x-plane [28]. Nevertheless, Equation 4 is a transcendental rather than an algebraic equation, of which the existence of exact solution on the complex plane is not definite. Such a transcendental equation can be only tackled through numerical analysis and, thus, numerical errors make it impossible to decide if the Kerker scattering demonstrated in Figure 3 is ideal or not in a mathematical sense. (iv) If an exact solution of Equation 4 exists, the chances of this solution being complex are much higher than it being purely real (real axes cover a tiny part of the complex plane). If an exact solution does not exist, the backward scattering is minimized more probably at complex arguments rather than at purely real ones. As a result, gain or loss are definitely helpful rather than harmful for the realizations of ideal Kerker scattering or suppression of backward scattering. (v) Discussing the exact solution of Equation 4 (and thus ideal Kerker scattering) is interesting and meaningful only mathematically. From a physical perspective, such an exploration is of very little significance, if not of no significance at all. This is because for realistic observations, there is no absolute boundary between exactly zero and approximately zero, which highly depends on the resolutions of different equipments. Moreover, when the scattering intensity gets smaller and smaller, the optical regime we study will shift from wave optics to quantum optics, where the quantum fluctuations would play a non-negligible role [39]. Then wave optics and, thus, Equation 4 itself breaks down and it becomes meaningless to discuss its exact solution.
Conclusion
We have proved that perfectly matching electric and magnetic multipoles of a specific order do not necessarily produce ideal Kerker scattering of exact zero backward scattering. This is because no matter how small the contributions from other multipoles are, they can never be made to be all zero or perfectly matched. In other words, to obtain zero backward scattering, we cannot just consider multipoles of a specific order. Instead we need to consider all contributing ones that are not exactly zero. It is further demonstrated that when multipoles of various order are simultaneously considered, loss or gain can be employed for suppression of backward scattering, serving as beneficial rather than detrimental contributions for the realization of ideal Kerker scattering. When Kerker scattering is achieved through the destructive interference among multipoles of several orders in the backward direction, rather than perfect multipole matching of each order, it is not synonymous with helicity conservation any more.
Funding
The following sources of funding are acknowledged: National Natural Science Foundation of China (Grant No. 11874026, and 11874426), and the Outstanding Young Researcher Scheme of National University of Defense Technology, and all authors thank the generous research funding for financial support.
References
-
Kerker, M.; Wang, D.-S.; Giles, C. L. J. Opt. Soc. Am. 1983, 73, 765. doi:10.1364/josa.73.000765
Return to citation in text: [1] [2] -
Jahani, S.; Jacob, Z. Nat. Nanotechnol. 2016, 11, 23–36. doi:10.1038/nnano.2015.304
Return to citation in text: [1] [2] [3] [4] -
Kuznetsov, A. I.; Miroshnichenko, A. E.; Brongersma, M. L.; Kivshar, Y. S.; Luk’yanchuk, B. Science 2016, 354, aag2472. doi:10.1126/science.aag2472
Return to citation in text: [1] [2] [3] [4] -
Liu, W.; Kivshar, Y. S. Opt. Express 2018, 26, 13085–13105. doi:10.1364/oe.26.013085
Return to citation in text: [1] [2] [3] [4] [5] [6] -
Tribelsky, M. I.; Miroshnichenko, A. E. Phys. Rev. A 2016, 93, 053837. doi:10.1103/physreva.93.053837
Return to citation in text: [1] -
Geffrin, J. M.; García-Cámara, B.; Gómez-Medina, R.; Albella, P.; Froufe-Pérez, L. S.; Eyraud, C.; Litman, A.; Vaillon, R.; González, F.; Nieto-Vesperinas, M.; Sáenz, J. J.; Moreno, F. Nat. Commun. 2012, 3, 1171. doi:10.1038/ncomms2167
Return to citation in text: [1] -
Fu, Y. H.; Kuznetsov, A. I.; Miroshnichenko, A. E.; Yu, Y. F.; Luk’yanchuk, B. Nat. Commun. 2013, 4, 1527. doi:10.1038/ncomms2538
Return to citation in text: [1] -
Person, S.; Jain, M.; Lapin, Z.; Sáenz, J. J.; Wicks, G.; Novotny, L. Nano Lett. 2013, 13, 1806–1809. doi:10.1021/nl4005018
Return to citation in text: [1] -
Smirnova, D.; Kivshar, Y. S. Optica 2016, 3, 1241–1255. doi:10.1364/optica.3.001241
Return to citation in text: [1] -
Chen, H.-T.; Taylor, A. J.; Yu, N. Rep. Prog. Phys. 2016, 79, 076401. doi:10.1088/0034-4885/79/7/076401
Return to citation in text: [1] -
Staude, I.; Schilling, J. Nat. Photonics 2017, 11, 274–284. doi:10.1038/nphoton.2017.39
Return to citation in text: [1] -
Kruk, S.; Kivshar, Y. ACS Photonics 2017, 4, 2638–2649. doi:10.1021/acsphotonics.7b01038
Return to citation in text: [1] -
Yang, Z.-J.; Jiang, R.; Zhuo, X.; Xie, Y.-M.; Wang, J.; Lin, H.-Q. Phys. Rep. 2017, 701, 1–50. doi:10.1016/j.physrep.2017.07.006
Return to citation in text: [1] -
Ding, F.; Pors, A.; Bozhevolnyi, S. I. Rep. Prog. Phys. 2018, 81, 026401. doi:10.1088/1361-6633/aa8732
Return to citation in text: [1] -
Chen, W.; Chen, Y.; Liu, W. Phys. Rev. Lett. 2019, 122, 153907. doi:10.1103/physrevlett.122.153907
Return to citation in text: [1] -
Sadrieva, Z.; Frizyuk, K.; Petrov, M.; Kivshar, Y.; Bogdanov, A. Phys. Rev. B 2019, 100, 115303. doi:10.1103/physrevb.100.115303
Return to citation in text: [1] -
Chen, W.; Yang, Q.; Chen, Y.; Liu, W. ACS Omega 2020, 5, 14157–14163. doi:10.1021/acsomega.0c01843
Return to citation in text: [1] [2] -
Poshakinskiy, A. V.; Poddubny, A. N. Phys. Rev. X 2019, 9, 011008. doi:10.1103/physrevx.9.011008
Return to citation in text: [1] -
Alaee, R.; Gurlek, B.; Albooyeh, M.; Martín-Cano, D.; Sandoghdar, V. Phys. Rev. Lett. 2020, 125, 063601. doi:10.1103/physrevlett.125.063601
Return to citation in text: [1] -
Ballantine, K. E.; Ruostekoski, J. Phys. Rev. Lett. 2020, 125, 143604. doi:10.1103/physrevlett.125.143604
Return to citation in text: [1] -
Zhu, T.; Shi, Y.; Ding, W.; Tsai, D. P.; Cao, T.; Liu, A. Q.; Nieto-Vesperinas, M.; Sáenz, J. J.; Wu, P. C.; Qiu, C.-W. Phys. Rev. Lett. 2020, 125, 043901. doi:10.1103/physrevlett.125.043901
Return to citation in text: [1] -
Fernandez-Corbaton, I. Opt. Express 2013, 21, 29885–29893. doi:10.1364/oe.21.029885
Return to citation in text: [1] [2] [3] -
Yang, Q.; Chen, W.; Chen, Y.; Liu, W. ACS Photonics 2020, 7, 1830–1838. doi:10.1021/acsphotonics.0c00555
Return to citation in text: [1] -
Lee, J. Y.; Miroshnichenko, A. E.; Lee, R.-K. Phys. Rev. A 2017, 96, 043846. doi:10.1103/physreva.96.043846
Return to citation in text: [1] -
Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] [8] [9] -
van de Hulst, H. C. Light Scattering by Small Particles; John Wiley & Sons: New York, NY, USA, 1957.
Return to citation in text: [1] [2] [3] [4] [5] -
Bohren, C. F.; Huffman, D. R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1983. doi:10.1002/9783527618156
Return to citation in text: [1] [2] [3] [4] -
Aleksandrov, A. D.; Kolmogorov, A. N.; Lavrent’ev, M. A. Mathematics: Its Content, Methods and Meaning; Dover Publications: Mineola, NY, USA, 1999.
Return to citation in text: [1] [2] -
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1995.
Return to citation in text: [1] [2] -
Olmos-Trigo, J.; Abujetas, D. R.; Sanz-Fernández, C.; Zambrana-Puyalto, X.; de Sousa, N.; Sánchez-Gil, J. A.; Sáenz, J. J. Phys. Rev. Res. 2020, 2, 043021. doi:10.1103/physrevresearch.2.043021
Return to citation in text: [1] [2] -
Liu, W. Phys. Rev. Lett. 2017, 119, 123902. doi:10.1103/physrevlett.119.123902
Return to citation in text: [1] [2] -
Luk'yanchuk, B.; Paniagua-Domínguez, R.; Kuznetsov, A. I.; Miroshnichenko, A. E.; Kivshar, Y. S. Philos. Trans. R. Soc., A 2017, 375, 20160069. doi:10.1098/rsta.2016.0069
Return to citation in text: [1] -
Tribelsky, M. I.; Miroshnichenko, A. E. Phys. Rev. A 2016, 93, 053837. doi:10.1103/physreva.93.053837
Return to citation in text: [1] -
Luk’yanchuk, B. S.; Voshchinnikov, N. V.; Paniagua-Domínguez, R.; Kuznetsov, A. I. ACS Photonics 2015, 2, 993–999. doi:10.1021/acsphotonics.5b00261
Return to citation in text: [1] -
Yang, Q.; Chen, W.; Chen, Y.; Liu, W. Laser Photonics Rev. 2021, 15, 2000496. doi:10.1002/lpor.202000496
Return to citation in text: [1] -
Olmos-Trigo, J.; Sanz-Fernández, C.; Bergeret, F. S.; Sáenz, J. J. Opt. Lett. 2019, 44, 1762–1765. doi:10.1364/ol.44.001762
Return to citation in text: [1] -
Fernandez-Corbaton, I.; Zambrana-Puyalto, X.; Tischler, N.; Vidal, X.; Juan, M. L.; Molina-Terriza, G. Phys. Rev. Lett. 2013, 111, 060401. doi:10.1103/physrevlett.111.060401
Return to citation in text: [1] -
Yang, Q.; Chen, W.; Chen, Y.; Liu, W. Phys. Rev. B 2020, 102, 155427. doi:10.1103/physrevb.102.155427
Return to citation in text: [1] -
Berry, M. V. Much Ado about Nothing: Optical Distortion Lines (Phase Singularities, Zeros, and Vortices). In Proc. SPIE 3487, International Conference on Singular Optics, Aug 3, 1998; Soskin, M. S., Ed.; International Society for Optics and Photonics, 1998; pp 1–5. doi:10.1117/12.317693
Return to citation in text: [1]
| 4. | Liu, W.; Kivshar, Y. S. Opt. Express 2018, 26, 13085–13105. doi:10.1364/oe.26.013085 |
| 31. | Liu, W. Phys. Rev. Lett. 2017, 119, 123902. doi:10.1103/physrevlett.119.123902 |
| 22. | Fernandez-Corbaton, I. Opt. Express 2013, 21, 29885–29893. doi:10.1364/oe.21.029885 |
| 35. | Yang, Q.; Chen, W.; Chen, Y.; Liu, W. Laser Photonics Rev. 2021, 15, 2000496. doi:10.1002/lpor.202000496 |
| 25. | Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205 |
| 1. | Kerker, M.; Wang, D.-S.; Giles, C. L. J. Opt. Soc. Am. 1983, 73, 765. doi:10.1364/josa.73.000765 |
| 2. | Jahani, S.; Jacob, Z. Nat. Nanotechnol. 2016, 11, 23–36. doi:10.1038/nnano.2015.304 |
| 3. | Kuznetsov, A. I.; Miroshnichenko, A. E.; Brongersma, M. L.; Kivshar, Y. S.; Luk’yanchuk, B. Science 2016, 354, aag2472. doi:10.1126/science.aag2472 |
| 4. | Liu, W.; Kivshar, Y. S. Opt. Express 2018, 26, 13085–13105. doi:10.1364/oe.26.013085 |
| 8. | Person, S.; Jain, M.; Lapin, Z.; Sáenz, J. J.; Wicks, G.; Novotny, L. Nano Lett. 2013, 13, 1806–1809. doi:10.1021/nl4005018 |
| 9. | Smirnova, D.; Kivshar, Y. S. Optica 2016, 3, 1241–1255. doi:10.1364/optica.3.001241 |
| 10. | Chen, H.-T.; Taylor, A. J.; Yu, N. Rep. Prog. Phys. 2016, 79, 076401. doi:10.1088/0034-4885/79/7/076401 |
| 11. | Staude, I.; Schilling, J. Nat. Photonics 2017, 11, 274–284. doi:10.1038/nphoton.2017.39 |
| 12. | Kruk, S.; Kivshar, Y. ACS Photonics 2017, 4, 2638–2649. doi:10.1021/acsphotonics.7b01038 |
| 13. | Yang, Z.-J.; Jiang, R.; Zhuo, X.; Xie, Y.-M.; Wang, J.; Lin, H.-Q. Phys. Rep. 2017, 701, 1–50. doi:10.1016/j.physrep.2017.07.006 |
| 14. | Ding, F.; Pors, A.; Bozhevolnyi, S. I. Rep. Prog. Phys. 2018, 81, 026401. doi:10.1088/1361-6633/aa8732 |
| 26. | van de Hulst, H. C. Light Scattering by Small Particles; John Wiley & Sons: New York, NY, USA, 1957. |
| 27. | Bohren, C. F.; Huffman, D. R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1983. doi:10.1002/9783527618156 |
| 6. | Geffrin, J. M.; García-Cámara, B.; Gómez-Medina, R.; Albella, P.; Froufe-Pérez, L. S.; Eyraud, C.; Litman, A.; Vaillon, R.; González, F.; Nieto-Vesperinas, M.; Sáenz, J. J.; Moreno, F. Nat. Commun. 2012, 3, 1171. doi:10.1038/ncomms2167 |
| 7. | Fu, Y. H.; Kuznetsov, A. I.; Miroshnichenko, A. E.; Yu, Y. F.; Luk’yanchuk, B. Nat. Commun. 2013, 4, 1527. doi:10.1038/ncomms2538 |
| 25. | Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205 |
| 5. | Tribelsky, M. I.; Miroshnichenko, A. E. Phys. Rev. A 2016, 93, 053837. doi:10.1103/physreva.93.053837 |
| 26. | van de Hulst, H. C. Light Scattering by Small Particles; John Wiley & Sons: New York, NY, USA, 1957. |
| 2. | Jahani, S.; Jacob, Z. Nat. Nanotechnol. 2016, 11, 23–36. doi:10.1038/nnano.2015.304 |
| 3. | Kuznetsov, A. I.; Miroshnichenko, A. E.; Brongersma, M. L.; Kivshar, Y. S.; Luk’yanchuk, B. Science 2016, 354, aag2472. doi:10.1126/science.aag2472 |
| 4. | Liu, W.; Kivshar, Y. S. Opt. Express 2018, 26, 13085–13105. doi:10.1364/oe.26.013085 |
| 26. | van de Hulst, H. C. Light Scattering by Small Particles; John Wiley & Sons: New York, NY, USA, 1957. |
| 27. | Bohren, C. F.; Huffman, D. R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1983. doi:10.1002/9783527618156 |
| 2. | Jahani, S.; Jacob, Z. Nat. Nanotechnol. 2016, 11, 23–36. doi:10.1038/nnano.2015.304 |
| 3. | Kuznetsov, A. I.; Miroshnichenko, A. E.; Brongersma, M. L.; Kivshar, Y. S.; Luk’yanchuk, B. Science 2016, 354, aag2472. doi:10.1126/science.aag2472 |
| 4. | Liu, W.; Kivshar, Y. S. Opt. Express 2018, 26, 13085–13105. doi:10.1364/oe.26.013085 |
| 25. | Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205 |
| 28. | Aleksandrov, A. D.; Kolmogorov, A. N.; Lavrent’ev, M. A. Mathematics: Its Content, Methods and Meaning; Dover Publications: Mineola, NY, USA, 1999. |
| 1. | Kerker, M.; Wang, D.-S.; Giles, C. L. J. Opt. Soc. Am. 1983, 73, 765. doi:10.1364/josa.73.000765 |
| 26. | van de Hulst, H. C. Light Scattering by Small Particles; John Wiley & Sons: New York, NY, USA, 1957. |
| 27. | Bohren, C. F.; Huffman, D. R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1983. doi:10.1002/9783527618156 |
| 39. | Berry, M. V. Much Ado about Nothing: Optical Distortion Lines (Phase Singularities, Zeros, and Vortices). In Proc. SPIE 3487, International Conference on Singular Optics, Aug 3, 1998; Soskin, M. S., Ed.; International Society for Optics and Photonics, 1998; pp 1–5. doi:10.1117/12.317693 |
| 24. | Lee, J. Y.; Miroshnichenko, A. E.; Lee, R.-K. Phys. Rev. A 2017, 96, 043846. doi:10.1103/physreva.96.043846 |
| 25. | Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205 |
| 36. | Olmos-Trigo, J.; Sanz-Fernández, C.; Bergeret, F. S.; Sáenz, J. J. Opt. Lett. 2019, 44, 1762–1765. doi:10.1364/ol.44.001762 |
| 15. | Chen, W.; Chen, Y.; Liu, W. Phys. Rev. Lett. 2019, 122, 153907. doi:10.1103/physrevlett.122.153907 |
| 16. | Sadrieva, Z.; Frizyuk, K.; Petrov, M.; Kivshar, Y.; Bogdanov, A. Phys. Rev. B 2019, 100, 115303. doi:10.1103/physrevb.100.115303 |
| 17. | Chen, W.; Yang, Q.; Chen, Y.; Liu, W. ACS Omega 2020, 5, 14157–14163. doi:10.1021/acsomega.0c01843 |
| 18. | Poshakinskiy, A. V.; Poddubny, A. N. Phys. Rev. X 2019, 9, 011008. doi:10.1103/physrevx.9.011008 |
| 19. | Alaee, R.; Gurlek, B.; Albooyeh, M.; Martín-Cano, D.; Sandoghdar, V. Phys. Rev. Lett. 2020, 125, 063601. doi:10.1103/physrevlett.125.063601 |
| 20. | Ballantine, K. E.; Ruostekoski, J. Phys. Rev. Lett. 2020, 125, 143604. doi:10.1103/physrevlett.125.143604 |
| 21. | Zhu, T.; Shi, Y.; Ding, W.; Tsai, D. P.; Cao, T.; Liu, A. Q.; Nieto-Vesperinas, M.; Sáenz, J. J.; Wu, P. C.; Qiu, C.-W. Phys. Rev. Lett. 2020, 125, 043901. doi:10.1103/physrevlett.125.043901 |
| 22. | Fernandez-Corbaton, I. Opt. Express 2013, 21, 29885–29893. doi:10.1364/oe.21.029885 |
| 23. | Yang, Q.; Chen, W.; Chen, Y.; Liu, W. ACS Photonics 2020, 7, 1830–1838. doi:10.1021/acsphotonics.0c00555 |
| 25. | Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205 |
| 17. | Chen, W.; Yang, Q.; Chen, Y.; Liu, W. ACS Omega 2020, 5, 14157–14163. doi:10.1021/acsomega.0c01843 |
| 22. | Fernandez-Corbaton, I. Opt. Express 2013, 21, 29885–29893. doi:10.1364/oe.21.029885 |
| 37. | Fernandez-Corbaton, I.; Zambrana-Puyalto, X.; Tischler, N.; Vidal, X.; Juan, M. L.; Molina-Terriza, G. Phys. Rev. Lett. 2013, 111, 060401. doi:10.1103/physrevlett.111.060401 |
| 38. | Yang, Q.; Chen, W.; Chen, Y.; Liu, W. Phys. Rev. B 2020, 102, 155427. doi:10.1103/physrevb.102.155427 |
| 26. | van de Hulst, H. C. Light Scattering by Small Particles; John Wiley & Sons: New York, NY, USA, 1957. |
| 27. | Bohren, C. F.; Huffman, D. R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1983. doi:10.1002/9783527618156 |
| 25. | Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205 |
| 25. | Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205 |
| 2. | Jahani, S.; Jacob, Z. Nat. Nanotechnol. 2016, 11, 23–36. doi:10.1038/nnano.2015.304 |
| 3. | Kuznetsov, A. I.; Miroshnichenko, A. E.; Brongersma, M. L.; Kivshar, Y. S.; Luk’yanchuk, B. Science 2016, 354, aag2472. doi:10.1126/science.aag2472 |
| 4. | Liu, W.; Kivshar, Y. S. Opt. Express 2018, 26, 13085–13105. doi:10.1364/oe.26.013085 |
| 4. | Liu, W.; Kivshar, Y. S. Opt. Express 2018, 26, 13085–13105. doi:10.1364/oe.26.013085 |
| 31. | Liu, W. Phys. Rev. Lett. 2017, 119, 123902. doi:10.1103/physrevlett.119.123902 |
| 32. | Luk'yanchuk, B.; Paniagua-Domínguez, R.; Kuznetsov, A. I.; Miroshnichenko, A. E.; Kivshar, Y. S. Philos. Trans. R. Soc., A 2017, 375, 20160069. doi:10.1098/rsta.2016.0069 |
| 33. | Tribelsky, M. I.; Miroshnichenko, A. E. Phys. Rev. A 2016, 93, 053837. doi:10.1103/physreva.93.053837 |
| 34. | Luk’yanchuk, B. S.; Voshchinnikov, N. V.; Paniagua-Domínguez, R.; Kuznetsov, A. I. ACS Photonics 2015, 2, 993–999. doi:10.1021/acsphotonics.5b00261 |
| 25. | Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205 |
| 25. | Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D. R.; Lasa-Alonso, J.; de Sousa, N.; García-Etxarri, A.; Sánchez-Gil, J. A.; Molina-Terriza, G.; Sáenz, J. J. Phys. Rev. Lett. 2020, 125, 073205. doi:10.1103/physrevlett.125.073205 |
| 29. | Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1995. |
| 30. | Olmos-Trigo, J.; Abujetas, D. R.; Sanz-Fernández, C.; Zambrana-Puyalto, X.; de Sousa, N.; Sánchez-Gil, J. A.; Sáenz, J. J. Phys. Rev. Res. 2020, 2, 043021. doi:10.1103/physrevresearch.2.043021 |
| 28. | Aleksandrov, A. D.; Kolmogorov, A. N.; Lavrent’ev, M. A. Mathematics: Its Content, Methods and Meaning; Dover Publications: Mineola, NY, USA, 1999. |
| 29. | Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed.; Cambridge University Press: Cambridge, UK, 1995. |
| 30. | Olmos-Trigo, J.; Abujetas, D. R.; Sanz-Fernández, C.; Zambrana-Puyalto, X.; de Sousa, N.; Sánchez-Gil, J. A.; Sáenz, J. J. Phys. Rev. Res. 2020, 2, 043021. doi:10.1103/physrevresearch.2.043021 |
© 2022 Yang et al.; licensee Beilstein-Institut.
This is an open access article licensed under the terms of the Beilstein-Institut Open Access License Agreement (https://www.beilstein-journals.org/bjnano/terms), which is identical to the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0). The reuse of material under this license requires that the author(s), source and license are credited. Third-party material in this article could be subject to other licenses (typically indicated in the credit line), and in this case, users are required to obtain permission from the license holder to reuse the material.