Abstract
The study of infrared absorption by linear gold nanoantennas fabricated on a Si surface with underlying SiO2 layers of various thicknesses allowed the penetration depth of localized surface plasmons into SiO2 to be determined. The value of the penetration depth derived experimentally (20 ± 10 nm) corresponds to that obtained from electromagnetic simulations (12.9–30.0 nm). Coupling between plasmonic excitations of gold nanoantennas and optical phonons in SiO2 leads to the appearance of new plasmon–phonon modes observed in the infrared transmission spectra the frequencies of which are well predicted by the simulations.
Introduction
Plasmonic metamaterials remain the object of keen interest both in fundamental and applied research due to their unique optical properties including negative and zero refraction, focusing, filtering, polarization manipulation, etc. [1-4]. They are considered as perspective solutions for possible device applications that involve super- and hyperlenses, and for energy concentrators, cloaking materials, sensors, and others. The morphology of the metastructures can be varied from simple planar elements to more complicated three-dimensional structures. Linear nanoantennas are commonly used in optical sensors due to relative simplicity of their fabrication [5-9]. At the same time, as compared to alternative nanoantenna geometries, the linear nanoantennas are highly demanded in sensing as they provide maximal local field amplification which is of prime importance for enhancing the optical response of the structure.
In a conventional design, the linear nanoantenna structures are represented by a 2D array of periodically arranged rods of metal (e.g., Au, Al, Ag) the typical length of which falls into the range from tens of nanometers to a few micrometers, while having a width of about 100 nm that is defined by conventional nanolithography used for nanoantenna fabrication. Such nanoantennas exhibit the effect of the localized surface plasmon resonance (LSPR), which is observed when the eigenfrequency of electron oscillations in nanoantenna coincide with the frequency of the exciting electromagnetic radiation. The LSPR yields a sharp increase of the local electromagnetic field magnitude near the nanoantenna surface that makes feasible to detect a small amount of alien substances located in the near field region of the nanoantenna [8-10].
The linear nanoantennas have uniaxial symmetry and, therefore, can be characterized by two LSPR modes. The transverse mode is polarized perpendicular to the antenna and has the energy localized in the optical domain of the electromagnetic spectrum. The energy of the longitudinal mode, which is polarized along the antenna, depends on the structural parameters (the length, width, and height of the antennas, as well as the distance between them), the dielectric function of surrounding media and substrate materials, and can be varied within a wide spectral range from visible to far infrared or terahertz frequencies [11-14]. Nanoantennas exhibiting the LSPR in the optical spectral range are already used for surface-enhanced Raman scattering (SERS) [15-19], and for fluorescence enhancements [20-22]. Nanoantennas with the LSPR energy located in the infrared spectral region are considered as promising nanostructures for the detection of small amounts of both organic (down to attomoles) and inorganic substances, including semiconductor nanocrystals [18,23-27]. In this approach serving as the basis for surface-enhanced IR spectroscopy, the IR response of various thin films and adsorbents due to coincidence of LSPR energies in the nanoantenna and vibrational states of a studied substance [28-30].
When the LSPR energy in metal nanostructures is close to the optical phonon energy of investigated substances or thin films, the effects of plasmon–phonon coupling are to be expected. Indeed, as it was is shown in [31], such a coupling may drastically increase (by a factor of 200) the scattering intensity in the near field of the metal (Pt) tip of an atomic force microscope at frequencies of the SiC surface optical (SO) phonons. The results of the theoretical study of coupling between the LSPR and SO phonon modes in the nanoantenna structures formed on a GaN substrate were also reported [32]. A significant increase of the phonon response (1900 times) at the SO phonon frequencies is observed for the structures with nanoantenna arrays fabricated on a 3 nm thick natural silicon oxide layer. This phenomenon is interpreted in terms of the coupling between the antenna's, plasmon resonance and surface phonon–polariton excitations [26]. Similar results were obtained for a thermal SiO2 layer having the thickness of 106 nm, for which the SO phonon mode at 1230 cm−1 was investigated [10]. Very recently, G. Cacciato et al. [33] have observed plasmon–phonon modes in TiO2 films with embedded Ag nanoparticles due to the coupling of longitudinal optical (LO) phonons in TiO2 with free carriers present in the vicinity of Ag nanoparticles.
It should be noticed that available literature exhibits a lack of information on the dependence of the LSPR energy on the oxide layer thickness and the LSPR localization depth. This paper presents a systematic experimental and numerical study for the dependence of the LSPR energy on the structural parameters of the gold nanoantenna arrays formed on Si substrates with SiO2 sublayers of a variable thickness. The character of this dependence allows establishing the peculiar features of plasmon-phonon interaction in the structures and determining the LSPR depth localization.
Experimental
The linear nanoantenna arrays with the aforementioned structural parameters providing the longitudinal LSPR energy in the range of 600–4500 cm−1 were fabricated using electron beam nanolithography. We employed the directly writing nanolithographic machine Raith-150 (Raith GmbH, Germany) using technological steps described in [34]. Because of technological restrictions, the operating area of the fabricated nanoantenna arrays was limited by 3 × 3 mm2. The structural parameters of the nanoantennas were controlled by scanning electron microscopy.
The IR transmission spectra of the fabricated Au nanoantenna arrays were measured in the frequency range of 600–4500 cm−1 by means of the FTIR spectrometer Bruker IFS-113v. The spectrometer provided the spectral resolution of 4 cm−1 and was combined with an IR microscope enabling to focus the infrared radiation to a spot with a diameter of 100 µm. A globar (SiC) was utilized as a source of IR radiation, which was registered with a cooled HgCdTe detector. The IR spectra of the nanoantenna structures were normalized to the signal from the substrate without nanoantennas. The measurements were carried out at room temperature.
The thickness of the SiO2 layers was determined by a conventional ellipsometric technique which provided an accuracy of 1 nm in the thickness evaluation.
Results and Discussion
In this work, a set of uniform nanoantenna arrays with different lengths ranging from 500 to 1900 nm was fabricated by using nanolithography. Typical SEM images of the resulting structures are illustrated in Figure 1. The nanoantennas had a height of 50 nm, which was specified by the thickness of the gold layer deposited in the nanolithographic process.
![[2190-4286-7-145-1]](/bjnano/content/figures/2190-4286-7-145-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: Typical SEM images of the fabricated Au nanoantennas for the mid-IR spectral region. Nanoantenna lengths: a) 500 nm, b) 1100 nm, c) 1900 nm.
Figure 1: Typical SEM images of the fabricated Au nanoantennas for the mid-IR spectral region. Nanoantenna le...
A relatively large transverse period of nanoantennas (ca. 4 μm) was chosen to exclude the interaction between neighboring Au nanoantennas in the transverse direction. On the contrary, in the vertical direction the gap between nanoantennas was as small as 100 nm to maximize their mutual coupling and intensify the electric field inside the gap. The same value of 100 nm was imposed on the nanoantenna width.
IR transmission spectra of the fabricated nanoantennas described above are shown in Figure 2. The spectra demonstrate distinct deep minima, the position of which corresponds to the LSPR energy.
![[2190-4286-7-145-2]](/bjnano/content/figures/2190-4286-7-145-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Typical IR transmission spectra of linear antennas with different lengths.
Figure 2: Typical IR transmission spectra of linear antennas with different lengths.
As predicted earlier [35], the experimentally determined LSPR wavelength depends linearly on the antenna length in a wide spectral range (Figure 3). Such behavior originates from the dipole resonance phenomenon, which states that linear nanoantennas effectively couple to the incident electromagnetic waves polarized along the nanoantenna axis when their wavelength coincides with the doubled antenna length [36]. This coupling also depends on the dielectric function of a surrounding medium that makes the LSPR energy different for nanoantennas backed by a bare Si substrate and when a SiO2 sublayer is introduced beneath the nanoantennas.
![[2190-4286-7-145-3]](/bjnano/content/figures/2190-4286-7-145-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: LSPR energy in nanoantenna arrays fabricated on bare Si surfaces as a function of the nanoantenna length.
Figure 3: LSPR energy in nanoantenna arrays fabricated on bare Si surfaces as a function of the nanoantenna l...
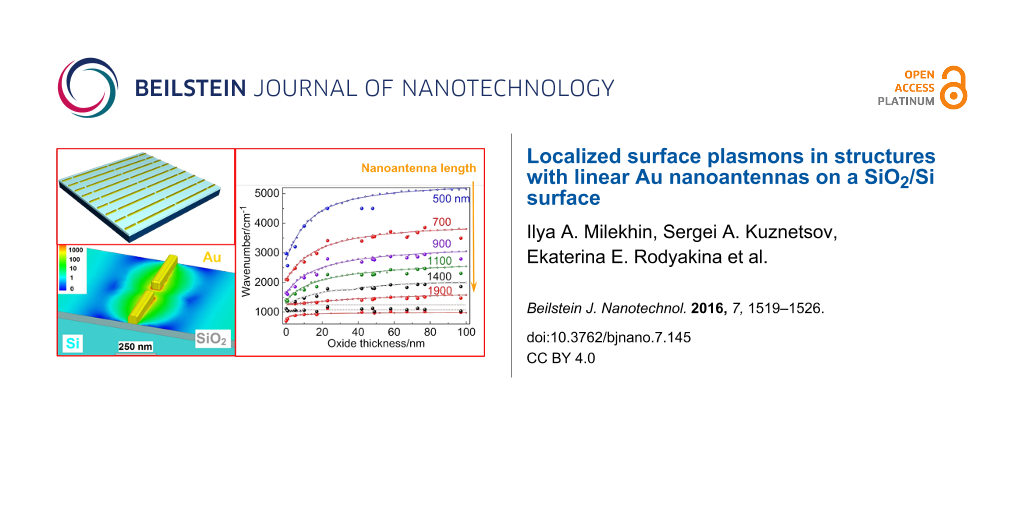
Figure 4 illustrates the relation between the LSPR frequency and the SiO2 layer thickness derived from the IR spectra of nanoantennas with the underlying SiO2 layer created on top of the Si substrate. It can be seen from Figure 4 that the LSPR frequency of the nanoantennas fabricated on a thick SiO2 layer is blue-shifted by about 1000 cm−1 with respect to the structures on bare Si due to the significant difference between the dielectric functions of Si and SiO2. With decreasing SiO2 layer thickness, starting from about 30 nm, a rapid transition from the LSPR energies derived for nanoantennas fabricated on a thick SiO2 layer, to the corresponding value in antennas on bare Si is observed (Figure 4). This is due to the fact that the effective dielectric function of the surrounding medium for the borderline case should be considered as a combination of the weighted dielectric functions of Si and SiO2 [37]. Thus, the oxide thickness of 20 ± 10 nm, for which significant changes in the LSPR frequency occur, defines the LSP penetration length.
![[2190-4286-7-145-4]](/bjnano/content/figures/2190-4286-7-145-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: LSPR frequencies of nanoantenna arrays versus the SiO2 thickness. Six structures with different antenna lengths ranging from 500 to 1900 nm are presented. Large circles: experiment; solid lines with dots: full-wave simulations.
Figure 4: LSPR frequencies of nanoantenna arrays versus the SiO2 thickness. Six structures with different ant...
In order to accurately examine influence of the SiO2 sublayer on the LSPR properties, the 3D full-wave electromagnetic simulations using ANSYS HFSS ™ v.15 software [38] were carried out in this work and distributions of the electromagnetic field near the nanoantenna surface were numerically studied. To model the nanoantenna array as a uniform periodic structure, we exploited a regime of Floquet ports and periodic boundary conditions applied to the structure unit cell. The nanoantennas were considered to be supported by a thin SiO2 layer with a thickness less than or equal to 100 nm formed on a silicon substrate. The dielectric functions of SiO2 and Si used in the simulations were taken from [37]. Gold was modeled as a lossy dispersive medium with the dielectric permittivity εAu described by the classical Drude formula:
where ν is the radiation frequency, and νp ≈ 72500 cm−1 and νc ≈ 216 cm−1 are the linear plasma frequency and the damping frequency, respectively [39].
In the simulations, the width b and the height t of the nanoantennas were assumed to be 50 nm with an the axial gap of a = 100 nm (see Figure 5a) as it was imposed by our nanofabrication. The nanoantennas were assigned to have rounded edges with a fillet radius of 15 nm. The thickness hSiO2 of the SiO2 layer was a variable parameter ranging within 0–100 nm. The transverse pitch gy of the nanoantennas was fixed as 5000 nm, while the nanoantenna lengths l of 500, 700, 900, 1100, 1400, and 1900 nm chosen for practical implementation were used in numerical simulations. The listed nanoantenna lengths (1400 and 1900 nm) secure the proximity of ther LSPR energy to the energy of optical phonons in SiO2. For the fixed structural parameters of the nanoantenna array, the simulations were aimed at determining the longitudinal LSPR frequency from the calculated IR transmission spectra of the structures with nanoantennas as a function of the SiO2 thickness. The results of these simulations are shown in Figure 4 (solid lines with dots). Quite good agreement between simulations and experiment can be deduced from the figure.
![[2190-4286-7-145-5]](/bjnano/content/figures/2190-4286-7-145-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: a) Structure geometry definition for the nanoantenna array (the unit cell is shown). b) Example of the distribution for the normalized electric field magnitude over SiO2 surface for the nanoantenna length l = 1100 nm. c) Similar E-field distribution referred to the vertical plane (XY) cutting the nanoantenna in the middle. d) Functional behavior of the near field decay along the OZ axis at the longitudinal LSPR frequency calculated for different nanoantenna lengths: 1: l = 500 nm, h SiO2 = 0 nm; 2: l = 500 nm, hSiO2 = 100 nm; 3: l = 700 nm, hSiO2 = 0 nm; 4: l = 700 nm, hSiO2 = 100 nm; 5: l = 900 nm, hSiO2 = 0 nm; 6: l = 900 nm, hSiO2 = 100 nm; 7: l = 1100 nm, hSiO2 = 0 nm; 8: l = 1100 nm, hSiO2 = 100 nm.
Figure 5: a) Structure geometry definition for the nanoantenna array (the unit cell is shown). b) Example of ...
Figure 5b illustrates the distribution of the electric field magnitude over the SiO2 surface within a unit cell of the nanoantenna array by the example of the antenna length l = 1100 nm and the SiO2 thickness hSiO2 = 100 nm. The distribution is simulated for the frequency of the longitudinal LSPR (2558 cm−1) and implies that the nanoantennas are excited normally by the electromagnetic wave polarized linearly along their axis. The field magnitude is normalized to that when the nanoantennas are removed from SiO2 surface, thereby yielding the relative E-field amplification distribution. Similarly, Figure 5c represents the simulated E-field distribution referred to the middle vertical plane (XY) and shows that the field penetrates to the SiO2 layer at a relatively small distance. Quantitatively, the LSPR penetration depth δLSPR in Si and SiO2 can be derived from Figure 5d, which shows plots of the E-field decay along the OZ axis simulated for different antenna lengths by the example of the two marginal cases: hSiO2 = 0 and 100 nm. As retrieved from the plots, the typical value of the E-field decay by the factor of e, herein referred to as δLSPR, falls within 12.5–13.9 nm and 14.4–16.6 nm for hSiO2 = 0 and 100 nm, respectively. It is noteworthy that functionally the E-decay behavior is fitted well not by a single exponent but by a sum of two exponents P1•exp(−z/δ1) and P2•exp(−z/δ2), which describe short-range (near-field) and long-range (far-field) components of the LSPR field, respectively [5]. For the presented plots, the values of δ1 and δ2 are correspondingly ranged within 4.7–8.9 nm and 30.1–51.3 nm, while the exponent amplitudes are characterized by the ratio P1/P2 ≈ 1.15–2.00 indicating predominance of the short-range field component.
When the nanoantenna structure is located on the interface between two semi-infinite dielectric media with the dielectric permittivities ε1 and ε2, its LSPR frequency νε1,ε2 undergoes a red shift relative to the similar frequency ν1,1 when nanoantennas are placed in free space. These frequencies are linked via the effective refractive index neff = [(ε1 + ε2)/2]1/2: νε1,ε2 = ν1,1/neff [12]. This allows one to conclude that when the nanoantennas are backed by a SiO2 layer the thickness of which is noticeably larger than the LSPR penetration depth δLSPR, the following relation between the LSPR frequencies νSi and νSiO2 corresponding to the cases of bare Si (hSiO2 = 0) and thick SiO2 layers should be valid:
Using data from Figure 4, it can be verified that for hSiO2 = 100 nm Equation 1 is satisfied with an accuracy of 5–7%.
It is noteworthy that the experimental and numerical data from Figure 4 are fitted well by allometric functions (solid lines) of the following kind:
where A1, A2, p, h0 are the constants. For the investigated nanoantenna structures, excluding the case of l = 1900 nm complicated by plasmon–phonon interactions, the exponent p changes from 1.15 down to 0.7 when the length varies from 500 to 1400 nm, while the characteristic length h0 of the allometric function alteration changes within 12.9–30.0 nm. The latter values are assessed to be in good concordance with the LSPR localization depth δLSPR and the “two exponents fit” established by us in numerical simulations.
It is important to highlight that the influence of the SiO2 layer thickness on the LSPR frequency of nanoantennas with the length of 1400 and 1900 nm becomes more complex in the vicinity of the TO and LO phonon frequencies in SiO2, which are 1070 and 1240 cm−1, respectively. The experimental and calculated IR transmission spectra of these structures are presented in Figure 6. As one can see from the figure, the IR spectrum of the structure with the thickness of a natural silicon oxide layer of 0.8 nm reveals a pronounced minimum at 700 cm−1 corresponding to the LSPR mode. A weaker feature located between the TO (1075 cm−1) and LO (1250 cm−1) phonon modes in SiO2 at 1230 cm−1 is assigned as a SO phonon mode according to earlier observations for nanoantennas on thin SiO2 [25]. However, with the increasing SiO2 layer thickness the position of LSPR is shifted towards higher frequencies. At a thickness of about 5 nm the LSPR mode splits into two modes. The low frequency mode (ω−) located at frequencies below the TO phonon modes approaches the frequency position of the TO phonon with increasing SiO2 layer thickness. The high frequency mode (ω+) splits off from the LO phonon frequency reaching the value of 1280 cm−1 for 5 nm thick SiO2. With further increase of the SiO2 layer thickness the ω+ mode asymptotically approaches the LSPR mode frequency. The calculated IR spectra shown in Figure 6b,d describe well the experimental results.
![[2190-4286-7-145-6]](/bjnano/content/figures/2190-4286-7-145-6.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: Experimental (a,c) and calculated (b,d) IR transmission spectra of nanoantenna array with the lengths of 1900 nm (a,b) and 1400 nm (c,d) fabricated on SiO2 layers of different thicknesses measured at normal incidence. The IR transmission spectrum of a 49 nm thick SiO2 layer on a Si substrate measured at off-normal (70°) incidence is shown for comparison. The vertical dashed lines indicate the frequency position of the TO, SO, and LO phonons in SiO2.
Figure 6: Experimental (a,c) and calculated (b,d) IR transmission spectra of nanoantenna array with the lengt...
The splitting of the LSPR modes due to the plasmon–phonon interaction is additionally illustrated in Figure 7, wherein the experimental points (circles) and simulated curves (solid lines with dots) show the frequency positions for the ω− and ω+ modes as a function of the SiO2 sublayer thickness plotted in the spectral range of optical phonons in SiO2. The graphs correspond to the nanoantenna length of 1400 and 1900 nm and reproduce Figure 4 at a larger scale. Note, the spectral splitting is a characteristic feature of coupling between plasmon excitations and optical phonons in heavily doped ionic semiconductors [40,41]. Here, instead of 3D plasmon excitations of free electron gas in doped semiconductors, we deal with the localized surface plasmon excitations induced by Au nanoantennas that interact with the bulk optical phonons in the SiO2 layer. Moreover, the SiO2 layer thickness governs the LSPR mode frequency in a similar manner as the free-carrier concentration specifies the plasmon frequency in ionic materials.
![[2190-4286-7-145-7]](/bjnano/content/figures/2190-4286-7-145-7.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 7: Splitting the LSPR modes due to plasmon–phonon interaction for nanoantennas with the lengths of 1400 and 1900 nm. Large circles: experiment; solid lines with dots: full-wave simulations.
Figure 7: Splitting the LSPR modes due to plasmon–phonon interaction for nanoantennas with the lengths of 140...
Conclusion
In this work, the dependence of the LSPR frequency on the thickness of the underlying SiO2 layer are thoroughly studied via analyzing the experimental and simulated IR transmission spectra for the arrays of linear nanoantennas with different lengths. The character of this dependence allowed us to determine the value of the penetration depth of about 20 nm for the localized surface plasmon in the SiO2 layer. It is found that the plasmon–phonon interaction leads to splitting the LSPR mode into two branches (low and high frequency) when its energy approaches to those of optical phonons in SiO2. The experimental data are demonstrated to be in good concordance with full-wave simulations in ANSYS HFSS™ electromagnetic software.
Acknowledgements
This study was supported by the Russian Science Foundation (project n.14-12-01037, in part of nanoantenna fabrication and structural characterization, IR measurements, and electromagnetic full-wave simulations) and the Ministry of Education and Science of the Russian Federation (State Assignment Contract #3002 in part of design development for nanoantenna structures using ANSYS HFSS™). The authors are thankful to K. P. Mogil’nikov for determining the SiO2 layer thickness using spectral ellipsometry and L. L.Sveshnikova for technical assistance.
References
-
Cai, W.; Shalaev, V. Optical Metamaterials: Fundamentals and Applications; Springer: New York, 2010. doi:10.1007/978-1-4419-1151-3
Return to citation in text: [1] -
Pendry, J. B. Phys. Rev. Lett. 2000, 85, 3966–3969. doi:10.1103/PhysRevLett.85.3966
Return to citation in text: [1] -
Belov, P. A.; Simovski, C. R.; Ikonen, P. Phys. Rev. B 2005, 71, 193105. doi:10.1103/PhysRevB.71.193105
Return to citation in text: [1] -
Porterfield, D. W.; Hesler, J. L.; Densing, R.; Mueller, E. R.; Crowe, T. W.; Weikle, R. M. Appl. Opt. 1994, 33, 6046–6052. doi:10.1364/AO.33.006046
Return to citation in text: [1] -
Adato, R.; Altug, H. Nat. Commun. 2013, 4, No. 2154. doi:10.1038/ncomms3154
Return to citation in text: [1] [2] -
Alonso-González, P.; Albella, P.; Neubrech, F.; Huck, C.; Chen, J.; Golmar, F.; Casanova, F.; Hueso, L. E.; Pucci, A.; Aizpurua, J.; Hillenbrand, R. Phys. Rev. Lett. 2013, 110, 203902. doi:10.1103/PhysRevLett.110.203902
Return to citation in text: [1] -
Selig, O.; Siffels, R.; Rezus, Y. L. A. Phys. Rev. Lett. 2015, 114, 233004. doi:10.1103/PhysRevLett.114.233004
Return to citation in text: [1] -
Pucci, A.; Neubrech, F.; Aizpurua, J.; Cornelius, T.; Lamy de la Chapelle, M. Electromagnetic Nanowire Resonances for Field-Enhanced Spectroscopy. In One-Dimensional Nanostructures; Wang, Z., Ed.; Springer: New York, 2008. doi:10.1007/978-0-387-74132-1_8
Return to citation in text: [1] [2] -
Lamy de la Chapelle, M.; Pucci, A., Eds. Nanoantenna: Plasmon - Enhanced Spectroscopies for Biotechnological Applications; CRC Press Taylor & Francis Group, 2013.
Return to citation in text: [1] [2] -
Levin, C. S.; Kundu, J.; Barhoumi, A.; Halas, N. J. Analyst 2009, 134, 1745–1750. doi:10.1039/b909080k
Return to citation in text: [1] [2] -
Biagioni, P.; Huang, J.-S.; Hecht, B. Rep. Prog. Phys. 2012, 75, 024402. doi:10.1088/0034-4885/75/2/024402
Return to citation in text: [1] -
Neubrech, F.; Kolb, T.; Lovrincic, R.; Fahsold, G.; Pucci, A.; Aizpurua, J.; Cornelius, T. W.; Toimil-Molares, M. E.; Neumann, R.; Karim, S. Appl. Phys. Lett. 2006, 89, 253104. doi:10.1063/1.2405873
Return to citation in text: [1] [2] -
Ayas, S.; Topal, A. E.; Cupallari, A.; Güner, H.; Bakan, G.; Dana, A. ACS Photonics 2014, 1, 1313–1321. doi:10.1021/ph500330x
Return to citation in text: [1] -
Razzari, L.; Toma, A.; Shalaby, M.; Clerici, M.; Zaccaria, R. P.; Liberale, C.; Marras, S.; Al-Naib, I. A. I.; Das, G.; De Angelis, F.; Peccianti, M.; Falqui, A.; Ozaki, T.; Morandotti, R.; Di Fabrizio, E. Opt. Express 2011, 19, 26088–26094. doi:10.1364/OE.19.026088
Return to citation in text: [1] -
Nie, S.; Emory, S. R. Science 1997, 275, 1102–1106. doi:10.1126/science.275.5303.1102
Return to citation in text: [1] -
Grand, J.; Lamy de la Chapelle, M.; Bijeon, J.-L.; Adam, P.-M.; Vial, A.; Royer, P. Phys. Rev. B 2005, 72, 033407. doi:10.1103/PhysRevB.72.033407
Return to citation in text: [1] -
Billot, L.; Lamy de la Chapelle, M.; Grimault, A.-S.; Vial, A.; Barchiesi, D.; Bijeon, J.-L.; Adam, P.-M.; Royer, P. Chem. Phys. Lett. 2006, 422, 303–307. doi:10.1016/j.cplett.2006.02.041
Return to citation in text: [1] -
D’Andrea, C.; Bochterle, J.; Toma, A.; Huck, C.; Neubrech, F.; Messina, E.; Fazio, B.; Maragò, O. M.; Di Fabrizio, E.; Lamy de La Chapelle, M.; Gucciardi, P. G.; Pucci, A. ACS Nano 2013, 7, 3522–3531. doi:10.1021/nn4004764
Return to citation in text: [1] [2] -
Cottat, M.; D’Andrea, C.; Yasukuni, R.; Malashikhina, N.; Grinyte, R.; Lidgi-Guigui, N.; Fazio, B.; Sutton, A.; Oudar, O.; Charnaux, N.; Pavlov, V.; Toma, A.; Di Fabrizio, E.; Gucciardi, P. G.; Lamy de la Chapelle, M. J. Phys. Chem. C 2015, 119, 15532–15540. doi:10.1021/acs.jpcc.5b03681
Return to citation in text: [1] -
Tam, F.; Goodrich, G. P.; Johnson, B. R.; Halas, N. J. Nano Lett. 2007, 7, 496–501. doi:10.1021/nl062901x
Return to citation in text: [1] -
Bakker, R. M.; Yuan, H.-K.; Liu, Z.; Drachev, V. P.; Kildishev, A. V.; Shalaev, V. M.; Pedersen, R. H.; Gresillon, S.; Boltasseva, A. Appl. Phys. Lett. 2008, 92, 043101. doi:10.1063/1.2836271
Return to citation in text: [1] -
Fort, E.; Grésillon, S. J. Phys. D 2008, 41, 013001. doi:10.1088/0022-3727/41/1/013001
Return to citation in text: [1] -
Wang, H.; Kundu, J.; Halas, N. J. Angew. Chem., Int. Ed. 2007, 46, 9040–9044. doi:10.1002/anie.200702072
Return to citation in text: [1] -
Neubrech, F.; Pucci, A.; Cornelius, T. W.; Karim, S.; García-Etxarri, A.; Aizpurua, J. Phys. Rev. Lett. 2008, 101, 157403. doi:10.1103/PhysRevLett.101.157403
Return to citation in text: [1] -
Neubrech, F.; Weber, D.; Enders, D.; Nagao, T.; Pucci, A. J. Phys. Chem. C 2010, 114, 7299–7301. doi:10.1021/jp908921y
Return to citation in text: [1] [2] -
Adato, R.; Yanik, A. A.; Amsden, J. J.; Kaplan, D. L.; Omenetto, F. G.; Hong, M. K.; Erramilli, S.; Altug, H. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 19227–19232. doi:10.1073/pnas.0907459106
Return to citation in text: [1] [2] -
Toma, A.; Tuccio, S.; Prato, M.; De Donato, F.; Perucchi, A.; Di Pietro, P.; Marras, S.; Liberale, C.; Zaccaria, R. P.; De Angelis, F.; Manna, L.; Lupi, S.; Di Fabrizio, E.; Razzari, L. Nano Lett. 2015, 15, 386–391. doi:10.1021/nl503705w
Return to citation in text: [1] -
Osawa, M.; Ataka, K.; Yoshii, K.; Nishikawa, Y. Appl. Spectrosc. 1993, 47, 1497–1502. doi:10.1366/0003702934067478
Return to citation in text: [1] -
Pucci, A.; Neubrech, F.; Weber, D.; Hong, S.; Toury, T.; Lamy de la Chapelle, M. Phys. Status Solidi B 2010, 247, 2071–2074. doi:10.1002/pssb.200983933
Return to citation in text: [1] -
Aouani, H.; Šipová, H.; Rahmani, M.; Navarro-Cia, M.; Hegnerová, K.; Homola, J.; Hong, M.; Maier, S. A. ACS Nano 2013, 7, 669–675. doi:10.1021/nn304860t
Return to citation in text: [1] -
Hillenbrand, R.; Taubner, T.; Keilmann, F. Nature 2002, 418, 159–162. doi:10.1038/nature00899
Return to citation in text: [1] -
Marty, R.; Mlayah, A.; Arbouet, A.; Girard, C.; Tripathy, S. Opt. Express 2013, 21, 4551–4559. doi:10.1364/OE.21.004551
Return to citation in text: [1] -
Cacciato, G.; Bayle, M.; Pugliara, A.; Bonafos, C.; Zimbone, M.; Privitera, V.; Grimaldi, M. G.; Carles, R. Nanoscale 2015, 7, 13468–13476. doi:10.1039/C5NR02406D
Return to citation in text: [1] -
Milekhin, A. G.; Yeryukov, N. A.; Sveshnikova, L. L.; Duda, T. A.; Rodyakina, E. E.; Gridchin, V. A.; Sheremet, E. S.; Zahn, D. R. T. Beilstein J. Nanotechnol. 2015, 6, 749–754. doi:10.3762/bjnano.6.77
Return to citation in text: [1] -
Novotny, L. Phys. Rev. Lett. 2007, 98, 266802. doi:10.1103/PhysRevLett.98.266802
Return to citation in text: [1] -
Bryant, G. W.; Garcıa de Abajo, F. J.; Aizpurua, J. Nano Lett. 2008, 8, 631–636. doi:10.1021/nl073042v
Return to citation in text: [1] -
Palik, E. D. Handbook of Optical Constants of Solids; Elsevier, 1998.
Return to citation in text: [1] [2] -
High Frequency Structure Simulator. ANSYS, Inc.. http://www.ansys.com/ (accessed July 14, 2016).
Return to citation in text: [1] -
Ordal, M. A.; Long, L. L.; Bell, R. J.; Bell, S. E.; Bell, R. R.; Alexander, R. W.; Ward, C. A. Appl. Opt. 1983, 22, 1099–1119. doi:10.1364/AO.22.001099
Return to citation in text: [1] -
Mooradian, A.; Wright, G. B. Phys. Rev. Lett. 1966, 16, 999–1001. doi:10.1103/PhysRevLett.16.999
Return to citation in text: [1] -
Li, Y. B.; Ferguson, I. T.; Stradling, R. A.; Zallen, R. Semicond. Sci. Technol. 1992, 7, 1149–1154. doi:10.1088/0268-1242/7/9/002
Return to citation in text: [1]
| 38. | High Frequency Structure Simulator. ANSYS, Inc.. http://www.ansys.com/ (accessed July 14, 2016). |
| 1. | Cai, W.; Shalaev, V. Optical Metamaterials: Fundamentals and Applications; Springer: New York, 2010. doi:10.1007/978-1-4419-1151-3 |
| 2. | Pendry, J. B. Phys. Rev. Lett. 2000, 85, 3966–3969. doi:10.1103/PhysRevLett.85.3966 |
| 3. | Belov, P. A.; Simovski, C. R.; Ikonen, P. Phys. Rev. B 2005, 71, 193105. doi:10.1103/PhysRevB.71.193105 |
| 4. | Porterfield, D. W.; Hesler, J. L.; Densing, R.; Mueller, E. R.; Crowe, T. W.; Weikle, R. M. Appl. Opt. 1994, 33, 6046–6052. doi:10.1364/AO.33.006046 |
| 15. | Nie, S.; Emory, S. R. Science 1997, 275, 1102–1106. doi:10.1126/science.275.5303.1102 |
| 16. | Grand, J.; Lamy de la Chapelle, M.; Bijeon, J.-L.; Adam, P.-M.; Vial, A.; Royer, P. Phys. Rev. B 2005, 72, 033407. doi:10.1103/PhysRevB.72.033407 |
| 17. | Billot, L.; Lamy de la Chapelle, M.; Grimault, A.-S.; Vial, A.; Barchiesi, D.; Bijeon, J.-L.; Adam, P.-M.; Royer, P. Chem. Phys. Lett. 2006, 422, 303–307. doi:10.1016/j.cplett.2006.02.041 |
| 18. | D’Andrea, C.; Bochterle, J.; Toma, A.; Huck, C.; Neubrech, F.; Messina, E.; Fazio, B.; Maragò, O. M.; Di Fabrizio, E.; Lamy de La Chapelle, M.; Gucciardi, P. G.; Pucci, A. ACS Nano 2013, 7, 3522–3531. doi:10.1021/nn4004764 |
| 19. | Cottat, M.; D’Andrea, C.; Yasukuni, R.; Malashikhina, N.; Grinyte, R.; Lidgi-Guigui, N.; Fazio, B.; Sutton, A.; Oudar, O.; Charnaux, N.; Pavlov, V.; Toma, A.; Di Fabrizio, E.; Gucciardi, P. G.; Lamy de la Chapelle, M. J. Phys. Chem. C 2015, 119, 15532–15540. doi:10.1021/acs.jpcc.5b03681 |
| 35. | Novotny, L. Phys. Rev. Lett. 2007, 98, 266802. doi:10.1103/PhysRevLett.98.266802 |
| 11. | Biagioni, P.; Huang, J.-S.; Hecht, B. Rep. Prog. Phys. 2012, 75, 024402. doi:10.1088/0034-4885/75/2/024402 |
| 12. | Neubrech, F.; Kolb, T.; Lovrincic, R.; Fahsold, G.; Pucci, A.; Aizpurua, J.; Cornelius, T. W.; Toimil-Molares, M. E.; Neumann, R.; Karim, S. Appl. Phys. Lett. 2006, 89, 253104. doi:10.1063/1.2405873 |
| 13. | Ayas, S.; Topal, A. E.; Cupallari, A.; Güner, H.; Bakan, G.; Dana, A. ACS Photonics 2014, 1, 1313–1321. doi:10.1021/ph500330x |
| 14. | Razzari, L.; Toma, A.; Shalaby, M.; Clerici, M.; Zaccaria, R. P.; Liberale, C.; Marras, S.; Al-Naib, I. A. I.; Das, G.; De Angelis, F.; Peccianti, M.; Falqui, A.; Ozaki, T.; Morandotti, R.; Di Fabrizio, E. Opt. Express 2011, 19, 26088–26094. doi:10.1364/OE.19.026088 |
| 36. | Bryant, G. W.; Garcıa de Abajo, F. J.; Aizpurua, J. Nano Lett. 2008, 8, 631–636. doi:10.1021/nl073042v |
| 8. | Pucci, A.; Neubrech, F.; Aizpurua, J.; Cornelius, T.; Lamy de la Chapelle, M. Electromagnetic Nanowire Resonances for Field-Enhanced Spectroscopy. In One-Dimensional Nanostructures; Wang, Z., Ed.; Springer: New York, 2008. doi:10.1007/978-0-387-74132-1_8 |
| 9. | Lamy de la Chapelle, M.; Pucci, A., Eds. Nanoantenna: Plasmon - Enhanced Spectroscopies for Biotechnological Applications; CRC Press Taylor & Francis Group, 2013. |
| 10. | Levin, C. S.; Kundu, J.; Barhoumi, A.; Halas, N. J. Analyst 2009, 134, 1745–1750. doi:10.1039/b909080k |
| 33. | Cacciato, G.; Bayle, M.; Pugliara, A.; Bonafos, C.; Zimbone, M.; Privitera, V.; Grimaldi, M. G.; Carles, R. Nanoscale 2015, 7, 13468–13476. doi:10.1039/C5NR02406D |
| 40. | Mooradian, A.; Wright, G. B. Phys. Rev. Lett. 1966, 16, 999–1001. doi:10.1103/PhysRevLett.16.999 |
| 41. | Li, Y. B.; Ferguson, I. T.; Stradling, R. A.; Zallen, R. Semicond. Sci. Technol. 1992, 7, 1149–1154. doi:10.1088/0268-1242/7/9/002 |
| 5. | Adato, R.; Altug, H. Nat. Commun. 2013, 4, No. 2154. doi:10.1038/ncomms3154 |
| 6. | Alonso-González, P.; Albella, P.; Neubrech, F.; Huck, C.; Chen, J.; Golmar, F.; Casanova, F.; Hueso, L. E.; Pucci, A.; Aizpurua, J.; Hillenbrand, R. Phys. Rev. Lett. 2013, 110, 203902. doi:10.1103/PhysRevLett.110.203902 |
| 7. | Selig, O.; Siffels, R.; Rezus, Y. L. A. Phys. Rev. Lett. 2015, 114, 233004. doi:10.1103/PhysRevLett.114.233004 |
| 8. | Pucci, A.; Neubrech, F.; Aizpurua, J.; Cornelius, T.; Lamy de la Chapelle, M. Electromagnetic Nanowire Resonances for Field-Enhanced Spectroscopy. In One-Dimensional Nanostructures; Wang, Z., Ed.; Springer: New York, 2008. doi:10.1007/978-0-387-74132-1_8 |
| 9. | Lamy de la Chapelle, M.; Pucci, A., Eds. Nanoantenna: Plasmon - Enhanced Spectroscopies for Biotechnological Applications; CRC Press Taylor & Francis Group, 2013. |
| 34. | Milekhin, A. G.; Yeryukov, N. A.; Sveshnikova, L. L.; Duda, T. A.; Rodyakina, E. E.; Gridchin, V. A.; Sheremet, E. S.; Zahn, D. R. T. Beilstein J. Nanotechnol. 2015, 6, 749–754. doi:10.3762/bjnano.6.77 |
| 31. | Hillenbrand, R.; Taubner, T.; Keilmann, F. Nature 2002, 418, 159–162. doi:10.1038/nature00899 |
| 26. | Adato, R.; Yanik, A. A.; Amsden, J. J.; Kaplan, D. L.; Omenetto, F. G.; Hong, M. K.; Erramilli, S.; Altug, H. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 19227–19232. doi:10.1073/pnas.0907459106 |
| 12. | Neubrech, F.; Kolb, T.; Lovrincic, R.; Fahsold, G.; Pucci, A.; Aizpurua, J.; Cornelius, T. W.; Toimil-Molares, M. E.; Neumann, R.; Karim, S. Appl. Phys. Lett. 2006, 89, 253104. doi:10.1063/1.2405873 |
| 28. | Osawa, M.; Ataka, K.; Yoshii, K.; Nishikawa, Y. Appl. Spectrosc. 1993, 47, 1497–1502. doi:10.1366/0003702934067478 |
| 29. | Pucci, A.; Neubrech, F.; Weber, D.; Hong, S.; Toury, T.; Lamy de la Chapelle, M. Phys. Status Solidi B 2010, 247, 2071–2074. doi:10.1002/pssb.200983933 |
| 30. | Aouani, H.; Šipová, H.; Rahmani, M.; Navarro-Cia, M.; Hegnerová, K.; Homola, J.; Hong, M.; Maier, S. A. ACS Nano 2013, 7, 669–675. doi:10.1021/nn304860t |
| 10. | Levin, C. S.; Kundu, J.; Barhoumi, A.; Halas, N. J. Analyst 2009, 134, 1745–1750. doi:10.1039/b909080k |
| 25. | Neubrech, F.; Weber, D.; Enders, D.; Nagao, T.; Pucci, A. J. Phys. Chem. C 2010, 114, 7299–7301. doi:10.1021/jp908921y |
| 18. | D’Andrea, C.; Bochterle, J.; Toma, A.; Huck, C.; Neubrech, F.; Messina, E.; Fazio, B.; Maragò, O. M.; Di Fabrizio, E.; Lamy de La Chapelle, M.; Gucciardi, P. G.; Pucci, A. ACS Nano 2013, 7, 3522–3531. doi:10.1021/nn4004764 |
| 23. | Wang, H.; Kundu, J.; Halas, N. J. Angew. Chem., Int. Ed. 2007, 46, 9040–9044. doi:10.1002/anie.200702072 |
| 24. | Neubrech, F.; Pucci, A.; Cornelius, T. W.; Karim, S.; García-Etxarri, A.; Aizpurua, J. Phys. Rev. Lett. 2008, 101, 157403. doi:10.1103/PhysRevLett.101.157403 |
| 25. | Neubrech, F.; Weber, D.; Enders, D.; Nagao, T.; Pucci, A. J. Phys. Chem. C 2010, 114, 7299–7301. doi:10.1021/jp908921y |
| 26. | Adato, R.; Yanik, A. A.; Amsden, J. J.; Kaplan, D. L.; Omenetto, F. G.; Hong, M. K.; Erramilli, S.; Altug, H. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 19227–19232. doi:10.1073/pnas.0907459106 |
| 27. | Toma, A.; Tuccio, S.; Prato, M.; De Donato, F.; Perucchi, A.; Di Pietro, P.; Marras, S.; Liberale, C.; Zaccaria, R. P.; De Angelis, F.; Manna, L.; Lupi, S.; Di Fabrizio, E.; Razzari, L. Nano Lett. 2015, 15, 386–391. doi:10.1021/nl503705w |
| 39. | Ordal, M. A.; Long, L. L.; Bell, R. J.; Bell, S. E.; Bell, R. R.; Alexander, R. W.; Ward, C. A. Appl. Opt. 1983, 22, 1099–1119. doi:10.1364/AO.22.001099 |
| 20. | Tam, F.; Goodrich, G. P.; Johnson, B. R.; Halas, N. J. Nano Lett. 2007, 7, 496–501. doi:10.1021/nl062901x |
| 21. | Bakker, R. M.; Yuan, H.-K.; Liu, Z.; Drachev, V. P.; Kildishev, A. V.; Shalaev, V. M.; Pedersen, R. H.; Gresillon, S.; Boltasseva, A. Appl. Phys. Lett. 2008, 92, 043101. doi:10.1063/1.2836271 |
| 22. | Fort, E.; Grésillon, S. J. Phys. D 2008, 41, 013001. doi:10.1088/0022-3727/41/1/013001 |
| 32. | Marty, R.; Mlayah, A.; Arbouet, A.; Girard, C.; Tripathy, S. Opt. Express 2013, 21, 4551–4559. doi:10.1364/OE.21.004551 |
© 2016 Milekhin et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Nanotechnology terms and conditions: (http://www.beilstein-journals.org/bjnano)