Abstract
We studied the electrical transport properties of Au-seeded germanium nanowires with radii ranging from 11 to 80 nm at ambient conditions. We found a non-trivial dependence of the electrical conductivity, mobility and carrier density on the radius size. In particular, two regimes were identified for large (lightly doped) and small (stronger doped) nanowires in which the charge-carrier drift is dominated by electron-phonon and ionized-impurity scattering, respectively. This goes in hand with the finding that the electrostatic properties for radii below ca. 37 nm have quasi one-dimensional character as reflected by the extracted screening lengths.
Results and Discussion
Synthetic germanium nanowires (Ge NWs) have been proposed as potential next-generation components for high-performance applications [1-3]. Besides representing prospective field-effect devices [4,5], they have attracted interest as building blocks for nanoscaled electrooptical components [6] and, due to their specific surface properties [4] can be envisaged as high-potential chemical and biological sensors as discussed for other types of semiconductor NWs [7-10].
Successful implementation of NWs into the aforementioned sensor technologies requires an optimized operation regime which will depend on the dimensionality of the electronic system. In particular, to ensure a significant electronic response to changes at the NW surface region, both the electrostatic screening length should be larger than the NW radius and the surface-to-volume ratio maximised [8]. This in turn will only be fulfilled for a certain range of screening lengths [7] and associated NW surface-to-volume ratios [8]. While the surface-to-volume ratio scales with NW radius and therefore can be controlled by adjusting synthesis conditions [11,12], the screening length depends on the density and dimensional character of the charge carriers in the NW [8]. Therefore it is crucial to investigate the charge transport properties in the NWs of choice as function of their radius R to identify their different operation regimes.
To this end, we carried out electrical characterization at ambient conditions of individual Au-seeded Ge NWs with R ranging from 11 to 80 nm (cf. Supporting Information File 1). By experimentally measuring the electrical conductivity, σNW, and field effect mobility, μNW, we were able to identify the dominant scattering mechanisms and the R-dependence of the electrostatic screening length.
Ge NWs used in this study were synthesized at 400 °C on anodized alumina supports using a Au nanoparticle seeded vapour-liquid-solid process [13]. TEM analysis revealed that the NWs are monocrystalline with uniform radius along the axis (Figure 1a), have predominant <110> growth direction and are covered with a thin native oxide layer (Figure 1b). Individual NWs were deposited on degenerately doped Si substrates with 300 nm thermally grown SiO2 on top and contacted lithographically with Ag electrodes [14] in a four-point-probe configuration (Figure 1c). The Si backside of the chip was used as global backgate. For each NW, four-point current–voltage and transfer characteristics were taken under ambient conditions. All NWs showed p-type transfer characteristics (Figure 1d) indicating that the majority charge carriers are holes (cf. Supporting Information File 1) which is consistent with the existing studies on similar VLS grown semiconducting NWs [15-17]. In particular, the doping in our NWs is predominantly through surface states (cf. Supporting Information File 1). Also, our previous work [14] showed that the carrier-distribution is uniform over length scales of several hundred nm’s along each NW unlike potentially expected for deliberately volume-doped Si NWs [18-21].
![[2190-4286-7-151-1]](/bjnano/content/figures/2190-4286-7-151-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: Characterization of Au-seeded Ge NWs. (a) TEM image of a Ge NW with an Au nanoparticle at the tip. (b) Higher magnification TEM image showing a NW with uniform crystalline structure covered by a thin native oxide layer. (c) SEM image of a four-terminal Ge NW device fabricated with 200 nm wide electrodes on top of a 30 nm radius wire. (d) Transfer curve taken at 0.5 V source-drain voltage for a 28 nm radius wire revealing p-type charge transport. Inset: four-point current–voltage characteristic of the same NW.
Figure 1: Characterization of Au-seeded Ge NWs. (a) TEM image of a Ge NW with an Au nanoparticle at the tip. ...
From the measured data, σNW, μNW and the carrier density, Nd, values were extracted and are plotted in Figure 2 as function of the NW radius R.
![[2190-4286-7-151-2]](/bjnano/content/figures/2190-4286-7-151-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Radius-dependent charge transport properties in Ge NWs. (a) Electrical conductivity, (b) mobility and (c) charge carrier density as function of the NW radius R. Dotted lines in (a) and (b) are a guide to the eye. Grey dashed line in (c) corresponds to the numerical fitting of Nd(R) with a power function.
Figure 2: Radius-dependent charge transport properties in Ge NWs. (a) Electrical conductivity, (b) mobility a...
σNW(R) showed a monotonous decrease by two orders of magnitude with increasing NW radius (Figure 2a). A change in the R-dependence was observed at about 36 to 37 nm. Notably, for the same R we find a maximum in the μNW(R) (Figure 2b). This qualitative change in the R-dependence for both σNW(R) and μNW(R) suggests a crossover in charge-carrier conduction. We note that the data in Figure 2a also confirms that surface-scattering is negligible at these radii, as the conductivity increases by orders of magnitude with radius reduction (an opposite dependence would have been expected otherwise).
To provide insight into the nature of this crossover, we first extract Nd(R) (cf. Supporting Information File 1) which is shown in Figure 2c. The measured carrier density in all cases exceeds the intrinsic doping level of bulk Ge (1.3 × 1013 cm−3 [22]), which indicates that the carrier-concentration is equivalent to the number density of ionized acceptor levels (surface–dopant concentration). Numerical fitting revealed Nd(R) ~ R−α with α = 3.05 ± 0.37 showing that large radius NWs are comparably lightly doped. We note that the carrier concentration in the NW depends on the surface-state density which can vary depending on the synthesis conditions [15,23,24]. Therefore, the radius dependence of the carrier concentration may vary in differently grown NWs.
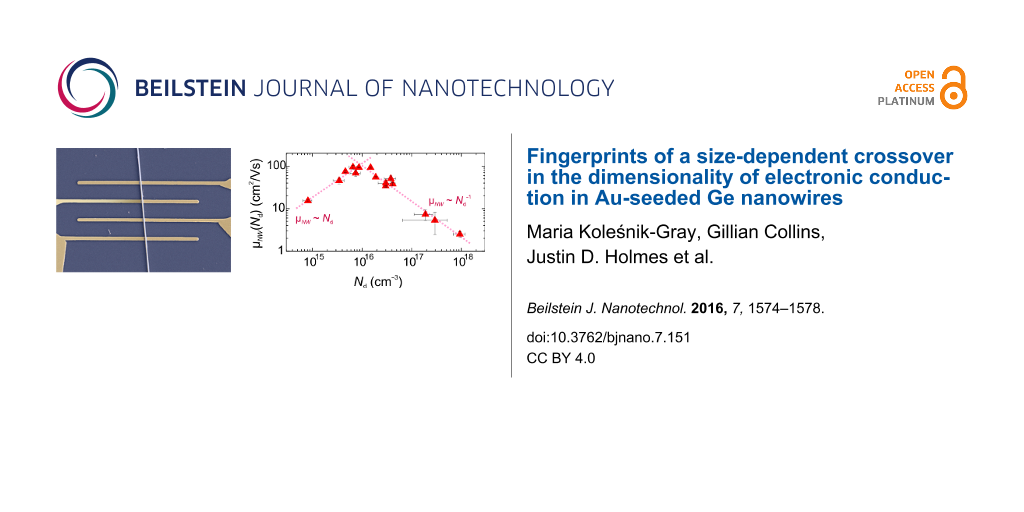
Since we found a non-trivial Nd(R) dependence, it is instructive to graph the conductivity and mobility as a function of carrier density, as is shown in Figure 3.
![[2190-4286-7-151-3]](/bjnano/content/figures/2190-4286-7-151-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: Carrier-density dependent transport properties in Ge NWs. (a) Electrical conductivity and (b) mobility as function of carrier density Nd. Dashed lines are a guide to the eye.
Figure 3: Carrier-density dependent transport properties in Ge NWs. (a) Electrical conductivity and (b) mobil...
For low dopant densities, σNW(Nd) first increases by two orders of magnitude, and for Nd exceeding ≈1016 cm−3 it enters into a slowly varying regime (Figure 3a). In the case of mobility (Figure 3b), between ≤1015 and ≈1016 cm−3 μNW(Nd) ≈ Nd, indicating that lattice phonon scattering is the main mechanism limiting the carrier drift [25]. The dominance of electron phonon scattering within this density range suggests that the free holes behave similar to those in (p-type) bulk Ge [18]. For higher Nd, however, which is characteristic of ionized impurities being the dominant scatterers [25]. This coincides with the slow-varying region in σNW(Nd) which indicates that a further augmentation in σNW(Nd) is inhibited due to the increased density of scattering centres which counterbalances the increasing Nd. Remarkably, in bulk p-Ge ionized impurity scattering is expected to contribute significantly over our entire experimental carrier-density range [22,25,26], which would, in contrast to our data, lead to a rather flat Nd dependence up to 1016 cm−3.
Having found the dominant scattering contributions for the limit of low and high-carrier densities in the NWs, we now address the electrostatic screening length. Assuming first that the charge carriers in the NWs follow a 3D-type of behaviour over the entire Nd range, we determine the corresponding 3D Debye (screening) length, , which is defined as [27]:
where εNW = 16 is the dielectric constant of the NW material (assumed the same as for bulk Ge [28]), ε0 the vacuum permittivity, kB the Boltzmann constant, T the temperature and q the electron charge.
In Figure 4, is plotted together with R as a function of Nd. For low-carrier densities,
is larger than the NW radius and shows a continuous decrease until it becomes comparable to R at about 1 to 2 × 1016 cm−3. From this point on
. However, a continued decrease in screening length would mean a reduction in the scattering cross-section, which is contradictory to the experimentally observed decrease in mobility (Figure 3b). Therefore this indicates that for higher Nd (smaller R) a 3D description of the electrostatics in the NW is not suitable anymore and thus the screening length has to be described by a lower dimensional scenario. Since in a NW a 2D description of the charge carriers is not a reasonable approach, the 1D screening length λ(1D) is better suited [29]. For our NWs, we can write
where εox ≈ 7.44 [27] is the dielectric constant of the native oxide, tox ≈ 3 nm (cf. Figure 1b) its thickness, and R(Nd) is the inverted Nd(R) ~ R−α (see above). That is, the screening length changes much slower with Nd compared to the 3D case.
Plotting λ(1D) also in Figure 4 we find a seamless matching of λ(1D) and at about 1 to 2 × 1016 cm−3 (equivalently R ≈ 35 to 38 nm) which falls close to both the maximum in μNW(Nd) and the entering into the slow varying regime of σNW(Nd) (Figure 3). We note that with increasing Nd, λ(1D) stays well above R which is consistent with the mobility decrease as well as the observed ionized impurity scattering dominating in this regime.
![[2190-4286-7-151-4]](/bjnano/content/figures/2190-4286-7-151-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4:
Characteristic length scales in Ge NWs. 3D Debye and 1D screening length λ(1D) as function of carrier density Nd. NW radius sizes (grey symbols) are plotted as a reference. Green triangles show the corresponding surface-to-volume ratios.
Figure 4:
Characteristic length scales in Ge NWs. 3D Debye and 1D screening length λ(1D) as function of carr...
Considering the potential application of the Au-seeded Ge NWs for sensors, Figure 4 also reveals the most suitable range of radii when plotting the surface-to-volume ratio also. Clearly, the quasi-1D regime is preferred as there the screening length is larger than R and the surface-to-volume ratio is maximised. In contrast, for radii ≥37 nm, the surface-to-volume ratio is by orders of magnitude lower, that is, not both prerequisites for an optimum sensor operation are met.
Summarizing, we demonstrated that the dominant scattering mechanisms and the electrostatic screening properties of Au-seeded VLS grown Ge NWs at room temperature are strongly dependent on their radius. Our results show that a crossover in charge carrier conduction occurs for carrier densities exceeding ≈1016 cm−3, equivalent to the radius decreasing below approximately 37 nm. Analysis of the electrical screening properties shows that this is associated with a shift from a 3D to quasi-1D regime where the carrier drift is limited predominantly by ionized impurity scatterers. This suggests that Ge NWs only in the quasi-1D regime can be expected to deliver high-performance sensor capabilities.
Supporting Information
| Supporting Information File 1: Extraction of intrinsic electrical transport parameters from measurement. | ||
| Format: PDF | Size: 308.1 KB | Download |
References
-
Barth, S.; Hernandez-Ramirez, F.; Holmes, J. D.; Romano-Rodriguez, A. Prog. Mater. Sci. 2010, 55, 563–627. doi:10.1016/j.pmatsci.2010.02.001
Return to citation in text: [1] -
Yu, B.; Sun, X. H.; Calebotta, G. A.; Dholakia, G. R.; Meyyappan, M. J. Cluster Sci. 2006, 17, 579–597. doi:10.1007/s10876-006-0081-x
Return to citation in text: [1] -
Lieber, C. M.; Wang, Z. L. MRS Bull. 2007, 32, 99–108. doi:10.1557/mrs2007.41
Return to citation in text: [1] -
Wang, D.; Wang, Q.; Javey, A.; Tu, R.; Dai, H.; Kim, H.; McIntyre, P. C.; Krishnamohan, T.; Saraswat, K. C. Appl. Phys. Lett. 2003, 83, 2432–2434. doi:10.1063/1.1611644
Return to citation in text: [1] [2] -
Greytak, A. B.; Lauhon, L. J.; Gudiksen, M. S.; Lieber, C. M. Appl. Phys. Lett. 2004, 84, 4176–4178. doi:10.1063/1.1755846
Return to citation in text: [1] -
Ahn, Y. H.; Park, J. Appl. Phys. Lett. 2007, 91, 162102. doi:10.1063/1.2799253
Return to citation in text: [1] -
Li, C.; Zhang, D.; Lui, X.; Han, S.; Tang, T.; Han, J.; Zhou, C. Appl. Phys. Lett. 2003, 82, 1613–1615. doi:10.1063/1.1559438
Return to citation in text: [1] [2] -
Kolmakov, A.; Zhang, Y.; Cheng, G.; Moskovits, M. Adv. Mater. 2003, 15, 997–1000. doi:10.1002/adma.200304889
Return to citation in text: [1] [2] [3] [4] -
Chen, X.; Wong, C. K. Y.; Yuan, C. A.; Zhang, G. Sens. Actuators, B 2013, 177, 178–195. doi:10.1016/j.snb.2012.10.134
Return to citation in text: [1] -
Cui, Y.; Wei, Q.; Park, H.; Lieber, C. M. Science 2001, 293, 1289–1292. doi:10.1126/science.1062711
Return to citation in text: [1] -
Ross, F. M. Rep. Prog. Phys. 2010, 73, 114501. doi:10.1088/0034-4885/73/11/114501
Return to citation in text: [1] -
Tuan, H.-Y.; Lee, D. C.; Korgel, B. A. Angew. Chem., Int. Ed. 2006, 45, 5184–5187. doi:10.1002/anie.200601078
Return to citation in text: [1] -
Collins, G.; Koleśnik, M.; Krstić, V.; Holmes, J. D. Chem. Mater. 2010, 22, 5235–5243. doi:10.1021/cm1012137
Return to citation in text: [1] -
Koleśnik-Gray, M. M.; Lutz, T.; Collins, G.; Biswas, S.; Holmes, J. D.; Krstić, V. Appl. Phys. Lett. 2013, 103, 153101. doi:10.1063/1.4821996
Return to citation in text: [1] [2] -
Hanrath, T.; Korgel, B. A. J. Phys. Chem. B 2005, 109, 5518–5524. doi:10.1021/jp044491b
Return to citation in text: [1] [2] -
Gu, G.; Burghard, M.; Kim, G. T.; Düsberg, G. S.; Chiu, P. W.; Krstić, V.; Roth, S.; Han, W. Q. J. Appl. Phys. 2001, 90, 5747–5751. doi:10.1063/1.1413495
Return to citation in text: [1] -
Wang, D.; Chang, Y.-L.; Wang, Q.; Cao, J.; Farmer, D. B.; Gordon, R. G.; Dai, H. J. Am. Chem. Soc. 2004, 126, 11602–11611. doi:10.1021/ja047435x
Return to citation in text: [1] -
Perea, D. E.; Hemesath, E. R.; Schwalbach, E. J.; Lensch-Falk, J. L.; Voorhees, P. W.; Lauhon, L. J. Nat. Nanotechnol. 2009, 4, 315–319. doi:10.1038/nnano.2009.51
Return to citation in text: [1] [2] -
Amit, I.; Givan, U.; Connell, J. G.; Paul, D. F.; Hammond, J. S.; Lauhon, L. J.; Rosenwaks, Y. Nano Lett. 2013, 13, 2598–2604. doi:10.1021/nl4007062
Return to citation in text: [1] -
Calahorra, Y.; Ritter, D. J. Appl. Phys. 2013, 114, 124310. doi:10.1063/1.4823517
Return to citation in text: [1] -
Schmidt, V.; Senz, S.; Gösele, U. Appl. Phys. A 2007, 86, 187–191. doi:10.1007/s00339-006-3746-2
Return to citation in text: [1] -
Sze, S. M. Physics of Semiconductor Devices, 2nd ed.; Wiley: New York, 1981.
Return to citation in text: [1] [2] -
Connaughton, S.; Hobbs, R.; Lotty, O.; Holmes, J. D.; Krstić, V. Adv. Mater. Interfaces 2015, 2, 1400469. doi:10.1002/admi.201400469
Return to citation in text: [1] -
Barth, S.; Koleśnik, M. M.; Donegan, K.; Krstić, V.; Holmes, J. D. Chem. Mater. 2011, 23, 3335–3340. doi:10.1021/cm200646e
Return to citation in text: [1] -
Dekker, A. J. Solid State Physics; Prentice-Hall, 1965.
Return to citation in text: [1] [2] [3] -
Brown, D. M.; Bray, R. Phys. Rev. 1962, 127, 1593–1602. doi:10.1103/PhysRev.127.1593
Return to citation in text: [1] -
Schroder, D. K. Semiconductor Material and Device Characterization, 3rd ed.; Wiley: Hoboken, New Jersey, 2006.
Return to citation in text: [1] [2] -
Knoch, J.; Mantl, S.; Appenzeller, J. Solid-State Electron. 2007, 51, 572–578. doi:10.1016/j.sse.2007.02.001
Return to citation in text: [1] -
Young, K. F.; Frederikse, H. P. R. J. Phys. Chem. Ref. Data 1973, 2, 313–409. doi:10.1063/1.3253121
Return to citation in text: [1]
| 1. | Barth, S.; Hernandez-Ramirez, F.; Holmes, J. D.; Romano-Rodriguez, A. Prog. Mater. Sci. 2010, 55, 563–627. doi:10.1016/j.pmatsci.2010.02.001 |
| 2. | Yu, B.; Sun, X. H.; Calebotta, G. A.; Dholakia, G. R.; Meyyappan, M. J. Cluster Sci. 2006, 17, 579–597. doi:10.1007/s10876-006-0081-x |
| 3. | Lieber, C. M.; Wang, Z. L. MRS Bull. 2007, 32, 99–108. doi:10.1557/mrs2007.41 |
| 7. | Li, C.; Zhang, D.; Lui, X.; Han, S.; Tang, T.; Han, J.; Zhou, C. Appl. Phys. Lett. 2003, 82, 1613–1615. doi:10.1063/1.1559438 |
| 8. | Kolmakov, A.; Zhang, Y.; Cheng, G.; Moskovits, M. Adv. Mater. 2003, 15, 997–1000. doi:10.1002/adma.200304889 |
| 9. | Chen, X.; Wong, C. K. Y.; Yuan, C. A.; Zhang, G. Sens. Actuators, B 2013, 177, 178–195. doi:10.1016/j.snb.2012.10.134 |
| 10. | Cui, Y.; Wei, Q.; Park, H.; Lieber, C. M. Science 2001, 293, 1289–1292. doi:10.1126/science.1062711 |
| 18. | Perea, D. E.; Hemesath, E. R.; Schwalbach, E. J.; Lensch-Falk, J. L.; Voorhees, P. W.; Lauhon, L. J. Nat. Nanotechnol. 2009, 4, 315–319. doi:10.1038/nnano.2009.51 |
| 19. | Amit, I.; Givan, U.; Connell, J. G.; Paul, D. F.; Hammond, J. S.; Lauhon, L. J.; Rosenwaks, Y. Nano Lett. 2013, 13, 2598–2604. doi:10.1021/nl4007062 |
| 20. | Calahorra, Y.; Ritter, D. J. Appl. Phys. 2013, 114, 124310. doi:10.1063/1.4823517 |
| 21. | Schmidt, V.; Senz, S.; Gösele, U. Appl. Phys. A 2007, 86, 187–191. doi:10.1007/s00339-006-3746-2 |
| 4. | Wang, D.; Wang, Q.; Javey, A.; Tu, R.; Dai, H.; Kim, H.; McIntyre, P. C.; Krishnamohan, T.; Saraswat, K. C. Appl. Phys. Lett. 2003, 83, 2432–2434. doi:10.1063/1.1611644 |
| 15. | Hanrath, T.; Korgel, B. A. J. Phys. Chem. B 2005, 109, 5518–5524. doi:10.1021/jp044491b |
| 16. | Gu, G.; Burghard, M.; Kim, G. T.; Düsberg, G. S.; Chiu, P. W.; Krstić, V.; Roth, S.; Han, W. Q. J. Appl. Phys. 2001, 90, 5747–5751. doi:10.1063/1.1413495 |
| 17. | Wang, D.; Chang, Y.-L.; Wang, Q.; Cao, J.; Farmer, D. B.; Gordon, R. G.; Dai, H. J. Am. Chem. Soc. 2004, 126, 11602–11611. doi:10.1021/ja047435x |
| 4. | Wang, D.; Wang, Q.; Javey, A.; Tu, R.; Dai, H.; Kim, H.; McIntyre, P. C.; Krishnamohan, T.; Saraswat, K. C. Appl. Phys. Lett. 2003, 83, 2432–2434. doi:10.1063/1.1611644 |
| 5. | Greytak, A. B.; Lauhon, L. J.; Gudiksen, M. S.; Lieber, C. M. Appl. Phys. Lett. 2004, 84, 4176–4178. doi:10.1063/1.1755846 |
| 14. | Koleśnik-Gray, M. M.; Lutz, T.; Collins, G.; Biswas, S.; Holmes, J. D.; Krstić, V. Appl. Phys. Lett. 2013, 103, 153101. doi:10.1063/1.4821996 |
| 11. | Ross, F. M. Rep. Prog. Phys. 2010, 73, 114501. doi:10.1088/0034-4885/73/11/114501 |
| 12. | Tuan, H.-Y.; Lee, D. C.; Korgel, B. A. Angew. Chem., Int. Ed. 2006, 45, 5184–5187. doi:10.1002/anie.200601078 |
| 13. | Collins, G.; Koleśnik, M.; Krstić, V.; Holmes, J. D. Chem. Mater. 2010, 22, 5235–5243. doi:10.1021/cm1012137 |
| 8. | Kolmakov, A.; Zhang, Y.; Cheng, G.; Moskovits, M. Adv. Mater. 2003, 15, 997–1000. doi:10.1002/adma.200304889 |
| 14. | Koleśnik-Gray, M. M.; Lutz, T.; Collins, G.; Biswas, S.; Holmes, J. D.; Krstić, V. Appl. Phys. Lett. 2013, 103, 153101. doi:10.1063/1.4821996 |
| 7. | Li, C.; Zhang, D.; Lui, X.; Han, S.; Tang, T.; Han, J.; Zhou, C. Appl. Phys. Lett. 2003, 82, 1613–1615. doi:10.1063/1.1559438 |
| 8. | Kolmakov, A.; Zhang, Y.; Cheng, G.; Moskovits, M. Adv. Mater. 2003, 15, 997–1000. doi:10.1002/adma.200304889 |
| 8. | Kolmakov, A.; Zhang, Y.; Cheng, G.; Moskovits, M. Adv. Mater. 2003, 15, 997–1000. doi:10.1002/adma.200304889 |
| 18. | Perea, D. E.; Hemesath, E. R.; Schwalbach, E. J.; Lensch-Falk, J. L.; Voorhees, P. W.; Lauhon, L. J. Nat. Nanotechnol. 2009, 4, 315–319. doi:10.1038/nnano.2009.51 |
| 15. | Hanrath, T.; Korgel, B. A. J. Phys. Chem. B 2005, 109, 5518–5524. doi:10.1021/jp044491b |
| 23. | Connaughton, S.; Hobbs, R.; Lotty, O.; Holmes, J. D.; Krstić, V. Adv. Mater. Interfaces 2015, 2, 1400469. doi:10.1002/admi.201400469 |
| 24. | Barth, S.; Koleśnik, M. M.; Donegan, K.; Krstić, V.; Holmes, J. D. Chem. Mater. 2011, 23, 3335–3340. doi:10.1021/cm200646e |
| 29. | Young, K. F.; Frederikse, H. P. R. J. Phys. Chem. Ref. Data 1973, 2, 313–409. doi:10.1063/1.3253121 |
| 27. | Schroder, D. K. Semiconductor Material and Device Characterization, 3rd ed.; Wiley: Hoboken, New Jersey, 2006. |
| 27. | Schroder, D. K. Semiconductor Material and Device Characterization, 3rd ed.; Wiley: Hoboken, New Jersey, 2006. |
| 28. | Knoch, J.; Mantl, S.; Appenzeller, J. Solid-State Electron. 2007, 51, 572–578. doi:10.1016/j.sse.2007.02.001 |
| 22. | Sze, S. M. Physics of Semiconductor Devices, 2nd ed.; Wiley: New York, 1981. |
| 25. | Dekker, A. J. Solid State Physics; Prentice-Hall, 1965. |
| 26. | Brown, D. M.; Bray, R. Phys. Rev. 1962, 127, 1593–1602. doi:10.1103/PhysRev.127.1593 |
© 2016 Koleśnik-Gray et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Nanotechnology terms and conditions: (http://www.beilstein-journals.org/bjnano)