Abstract
Molecular polarity governs lipophilicity, which in turn determines important agrochemical and environmental properties, such as soil sorption and bioconcentration of organic compounds. Since the C–F bond is the most polar in organic chemistry, the orientation of fluorine substituents originating from the rotation around C–C(F) bonds should affect the polarity and, consequently, the physicochemical and biological properties of fluorine-containing agrochemicals. Accordingly, this study aims to determine the most likely conformers of some fluorine-containing agrochemicals and to correlate their molecular dipole moments with the respective n-octanol/water partition coefficients (log P), in order to investigate the dependence of the lipophilicity with the molecular conformation.

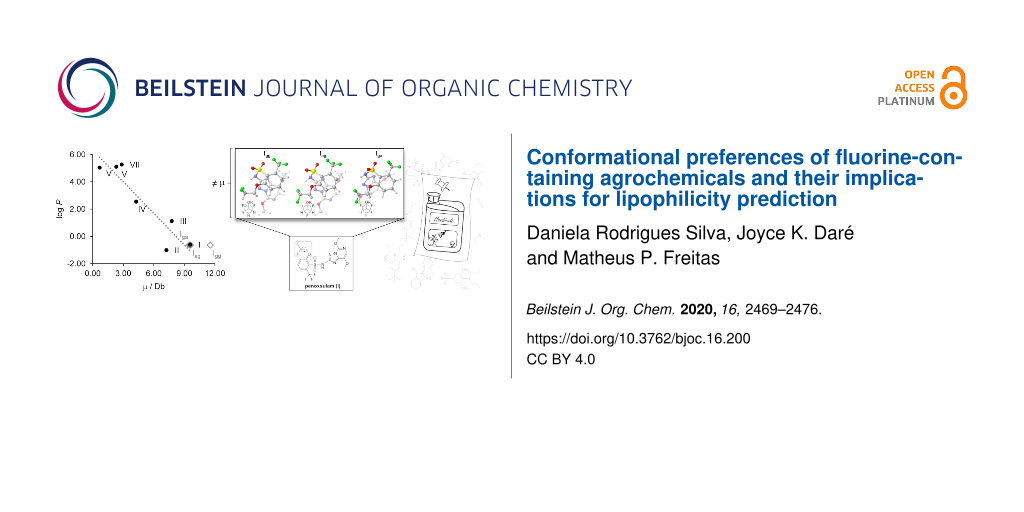
Graphical Abstract
Introduction
Whilst in the last years the agrochemical industry has encountered a period of downturn affected by new regulations, low crop prices, biochemical resistance, among other variables, recent events have shown signs of recovery [1]. Currently, the agrochemical industry focuses on introducing new efficient and more environmentally friendly products, that attend the new regulation requirements, for replacing those agrochemicals that were banned due to either their hazard or inefficiency in fighting persistent weeds and pathogens [1]. However, the process for designing, developing, and introducing new agrochemicals to the market is considerably challenging, since it involves many steps and the optimization of a range of properties. Furthermore, it is also an expensive and time-consuming procedure [2].
Fluorination is a common strategy employed as part of the optimization process during the design of new chemical compounds, which includes the modulation of a variety of properties such as lipophilicity, biological half-life, and biosorption [3,4]. This role helps in explaining the expressive amount of fluorine-containing agrochemical candidates (around 30%) as well as pharmaceuticals (around 20%) [5,6]. In this sense, the chemistry of fluorine-containing compounds has been extensively investigated in order to better understand the effects of fluorination on conformation, membrane permeation, pharmacokinetic properties, among other parameters [7].
From a conformational analysis point of view, the fluorine atom presents minimal steric effects; on the other hand, due to its high electronegativity, the C–F bond is highly polarized, which characterizes it as a site for electrostatic and hyperconjugative interactions [8]. Additionally, Juaristi and Notario [9] and O’Hagan and co-workers [10] have highlighted the crucial role of hyperconjugative interactions involving the fluorine lone pair in explaining the chemical behavior of organofluorine molecules and their unusual physicochemical properties. Lastly, Müller [11] explained that these features along with fluorine’s strict monovalent binding mode and little polarizability, when covalently bound, guarantee fluorination the well-known ability of modulating physicochemical properties.
Although the stereochemical effects of fluorination, responsible for specific interactions and conformational preferences of several groups of compounds, have become increasingly well understood [12], their direct implication on physicochemical properties has not been fully investigated yet. The orientation of fluorine substituents originated from the rotation of fluorine-containing C–C bonds should affect the polarity and, therefore, the physicochemical and biological properties of organofluorine compounds. However, there is a lack of studies that explain how these well-known conformational effects directly alter macroscopic observed properties, such as lipophilicity [13].
Accordingly, the main goal of this work is to investigate the relationship between lipophilicity and molecular conformation on a set of organofluorine agrochemicals. To this end, this study has been divided in two parts. First, we have analyzed the conformational equilibrium of penoxsulam (I, Figure 1). This compound has a 1,2–disubstituted ethane motif that could adopt three main staggered conformations, namely Igg, Iag and Iga (g = gauche and a = anti; see Figure 1), thus we have explored the intramolecular interactions governing its conformational preferences. It is worth mentioning that Igg has two gauche relationships between C–F and C–O bonds, which is stabilized by σCH → σCF/CO hyperconjugative interactions [14]. Second, we have searched for the implications of the relative conformational stabilities for log P prediction, the most common parameter employed to describe lipophilicity. It has been previously established that the lipophilicity of a compound depends greatly on the overall molecular polarity [15], which is often expressed as the molecular dipole moment (μ). In turn, the orientation of polar bonds also influences the overall polarity of an organic molecule, as above mentioned. Therefore, this work also seeks to assess a correlation between calculated μ values and experimental log P measures, in order to unveil the dependence of lipophilicity with molecular conformation.
Figure 1: Chemical structure of penoxsulam (I) and the main staggered conformations along the two F–C–C–O torsional angles (i.e., Igg, Iag, and Iga; g = gauche and a = anti).
Figure 1: Chemical structure of penoxsulam (I) and the main staggered conformations along the two F–C–C–O tor...
Results and Discussion
Conformational analysis of penoxsulam
Given the high degree of freedom in the chemical structure of penoxsulam (I), the conformational analysis started with a Monte Carlo conformational search at the ωB97X-D/6-31G(d,p) [16,17] level of the density functional theory (DFT). The global energy minimum conformation was then re-optimized in a higher level of theory, ωB97X-D/6-311++G(d,p) [16,18], resulting in conformer Iag (Figure 2). This conformer has one fluorine atom in an anti-orientation and the other one in a gauche-orientation relative to the vicinal oxygen atom (pointing towards the amine hydrogen atom). To evaluate the other possible conformations along the 1,2-disubstituted ethane motif, the C–C(F) bond was rotated to additionally obtain conformers Igg and Iga, and the corresponding geometries were then optimized. The resulting geometries and relative conformational energies are summarized in Figure 2.
![[1860-5397-16-200-2]](/bjoc/content/figures/1860-5397-16-200-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Optimized structures of conformers Igg (left), Iag (middle), and Iga (right), along with the relative electronic and Gibbs free energies (in kcal mol−1) in the gas phase and in water solution (in parentheses), computed at the ωB97X-D/6-311++G(d,p) level of theory.
Figure 2: Optimized structures of conformers Igg (left), Iag (middle), and Iga (right), along with the relati...
At first, we observe that the overall geometry is quite similar among the three conformers. Only for Iga, where the gauche fluorine atom points to the opposite direction of the amine group, the triazole ring was farther away from the 1,2-disubstituted ethane moiety. Note that the gas-phase relative conformational energy ΔE increases, i.e., becomes less stabilizing, in the order Iag < Iga < Igg. The difference in energy between Iag and Iga is somehow small (0.5 kcal mol−1), and these conformers are equally stable according to the relative Gibbs free energy ΔG (Boltzmann populations of 50% and 49%, respectively). The inclusion of an implicit polar solvent (e.g. water), however, decreases the difference in energy among conformers and Igg becomes the most stable conformer in solution, i.e., a double gauche effect takes place (see data in parentheses in Figure 2). This is not surprising, since Igg has the highest dipole moment (data shown in the next section) and is naturally more stabilized by polar solvents. Therefore, further analysis will consider the gas phase, since in this way we are accounting for the intrinsic intramolecular interactions without the influence of solvent as an external factor.
To better understand the relative conformational stabilities, we performed a numerical experiment in which the C–C(F) bond is rotated from conformer Iag keeping other geometrical parameters fixed. In this way, we can specifically investigate the intramolecular interactions governing conformational preferences in the 1,2–disubstituted ethane motif. Furthermore, we decomposed the conformational energy along rotation around the C–C(F) bond within the framework of the natural bond orbital (NBO) analysis [19] into the Lewis (ΔEL, which accounts for classical interactions) and non-Lewis (ΔENL, which accounts for delocalization energy) contributions (Figure 3). Note that all energy terms are represented relative to the conformation with the φO–C–C–H torsional angle of 0°, thus positive values mean that the energy becomes less stabilizing and negative values mean that the energy becomes more stabilizing.
![[1860-5397-16-200-3]](/bjoc/content/figures/1860-5397-16-200-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: Energy profile for the rotation around the C–C(F) bond and NBO analysis project onto the φO–C–C–H torsional angle (step size of 30°) at the ωB97X-D/6-311G(d,p) level of theory.
Figure 3: Energy profile for the rotation around the C–C(F) bond and NBO analysis project onto the φO–C–C–H t...
From Figure 3, it can be observed that conformer Igg is the most stabilized by the ΔENL term, which can be attributed to the stabilizing interactions featured in the gauche effect [14,20], due to the gauche arrangement along the two F–C–C–O pathways. The charge transfer from the filled σCH orbital to the empty σ*CF or σ*CO orbitals amounts to 4.6/4.5 and 3.3 kcal mol−1, respectively, which are more stabilizing than the corresponding σCF/CO → σ*CO/CF and nF/O → σ*CO/CF in the anti-orientation (Table 1). Note that the nF → σ*CO charge transfer is slightly more stabilizing than the σCF → σ*CO, which is in agreement with the findings of Juaristi and Notario [9], and O’Hagan and co-workers [10]. Besides, there is also an interaction between the fluorine electron lone pair nF and the σ*NH orbital of the amine group (of 3.2 kcal mol−1, see Table 1). Iga also experiences this stabilizing hydrogen bond-like intramolecular interaction (nF → σNH of 2.8 kcal mol–1, see Table 1). Yet, conformer Igg is not the global energy minimum. This is surprising, because all-gauche conformations in fluoropropanediol are strongly preferred [21], while the double gauche effect in difluoroethylamine and its hydrochloride salt stabilizes the gg over ag conformations [22]. Therefore, Iag is the global energy minimum because it experiences a more stabilizing ΔEL term. Among the three conformers, Igg has the least stabilizing ΔEL energy, and this can be ascribed to the closer proximity between the F and O electronegative atoms. Thus, the least stabilizing ΔEL term overcomes the stabilization from hyperconjugation interactions (ΔENL), and classical electrostatic and steric interactions are the main factors governing conformational preferences of penoxsulam (I).
Table 1: Second order perturbation energy E(2) of the main hyperconjugation interactions (in kcal mol–1) computed at the ωB97X-D/6-311G(d,p) level of theory.
| Conf. | σCH → σ*CF | σCH → σ*CO | σCO → σ*CF | σCF → σ*CO | nF → σ*CO | nO → σ*CF | nF → σ*NH |
| Igg | 4.6/4.5 | 3.3 | – | – | – | – | 3.2 |
| Iag | 4.7 | – | 1.5 | 1.5 | 1.8 | 0.8 | 2.8 |
| Iga | 4.3 | – | 1.7 | 1.4 | 1.6 | 0.8 | – |
It is worth mentioning that the structure of penoxsulam in the biological environment is already known in the literature [23] and, accordingly, it differs from the energy minimum conformations computed in this work. However, a conformational search in the gas phase, as performed herein, is necessary to fully understand the intramolecular interactions and to establish the correlation between μ and log P, since this physicochemical property does not depend on the geometry of penoxsulam inside a biological receptor.
Effect of molecular conformation on log P
Herein, we aim at evaluating the correlation of molecular conformation with lipophilicity, described in terms of the n-octanol/water partition coefficient – log P, through molecular dipole moment (μ). The molecular dipole moment, μ is a relatively simple parameter that can inform on subtle intramolecular interactions that favor one structural arrangement over another, as previously mentioned. Therefore, by using a weighted average μ over the most likely conformations to correlate with experimental log P, one can assess the dependence of log P with molecular conformation.
Accordingly, a consistent set of fluorine-containing agrochemicals (Figure 4) with experimentally available log P data was selected from a single database [24], which comprises: penoxsulam (I), pyroxsulam (II), cloransulam-methyl (III), flumioxazin (IV), fluroxypyr-1-methylheptyl ester (V), ethalfluralin (VI), and trifluralin (VII). The data set contains compounds without rotatable C–C(F) bonds (III–V), with a rotatable C–C(F) bond that does not generate different conformers (II, VI, and VII), and with a rotatable C–C(F) bond that generates different conformers (I). The μ values for all herbicides were computed through theoretical calculations (see computational details section) and are presented in Table 2 along with their respective experimental log P data.
Figure 4: Chemical structure of the agrochemicals I–VII analyzed herein.
Figure 4: Chemical structure of the agrochemicals I–VII analyzed herein.
Table 2: Experimental log P, dipole moment (μ, in Db), and predicted log P of agrochemicals I–VII.
| Compd. | log Pa | μb | milog Pc |
| Igg [0.01] | −0.60 | 11.56 | 2.74 |
| Iag [0.50] | −0.60 | 9.61 | 2.74 |
| Iga [0.49] | −0.60 | 9.50 | 2.74 |
| II | −1.01 | 7.24 | 1.44 |
| III | 1.12 | 7.76 | 3.09 |
| IV | 2.55 | 4.27 | 2.12 |
| V | 5.04 | 0.68 | 5.43 |
| VI | 5.11 | 2.32 | 4.28 |
| VII | 5.27 | 2.85 | 4.47 |
aExperimental log P obtained from the Dow AgroSciences database [24]; bdipole moments computed at the ωB97X-D/6-311++G(d,p) level of theory, see computational section for details; cpredicted log P calculated in the Molinspiration Cheminformatics server [25].
Penoxsulam (I) has a rotatable C–C(F) bond (as analyzed in the previous section) and, consequently, has the dependence of the molecular dipole moment μ with the rotation around this bond. It is well-known that μ is influenced by two main factors: the molecular dimensions and the electron distribution [26]. Thus, a different μ was calculated for each of the three staggered conformers of I and a weighted average μ was obtained from the calculated μ of the three conformers Igg, Iag, and Iga. Then, the calculated μ values were plotted against the experimental log P (Figure 5a) in order to quantitatively analyze the correlation between the two parameters. The resulting linear regression coefficient (r2) was 0.86, which can be considered a suitable correlation coefficient. A hypothesis test for the significance of the observed correlation, based on the p-value (at a significance level of 95%, α = 0.05), was also carried out. A p-value of 0.00264 was obtained, which is much smaller than the critical value of 0.05. Therefore, the null hypothesis (that considers the correlation coefficient as 0) is rejected, which reinforces the dependence of lipophilicity on the total molecular polarity.
![[1860-5397-16-200-5]](/bjoc/content/figures/1860-5397-16-200-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: Correlation between the experimental log P of agrochemicals I–VII and a) dipole moment (for I, μ is used as a weighted average of the conformers Igg, Iag, and Iga), and b) predicted log P (milog P).
Figure 5: Correlation between the experimental log P of agrochemicals I–VII and a) dipole moment (for I, μ is...
In another attempt to demonstrate the importance of μ (a conformational dependent parameter) for estimating log P, we employed the Molinspiration Cheminformatics tool [25] to predict log P, and the results are displayed in Table 2. The predicted outcomes were also plotted against the experimental values (see Figure 5b). Most tools for predicting physicochemical properties are based on the additive contributions of polarity from atoms or chemical groups instead of considering the overall molecular polarity (μ) [27]. The predictive ability of these methods for compounds with higher structural complexity have been questioned in the literature [28]. Indeed, the obtained r2 (0.72) exhibits a considerably higher discrepancy than that correlation obtained from μ when compared to the optimal value of 1. A linear regression of experimental log P against calculated log P values obtained from another source (the ChemSketch module of the ACD/Labs program) yields a similar result (r2 = 0.71, see Figure S1 in Supporting Information File 1). Moreover, from Figure 5b, due to the high slope and the resulting intercept, one can assume the existence of a systematic error associated with the prediction of log P. This finding reinsures the issues with additive methods for predicting lipophilicity of complex structures as those analyzed herein.
Nevertheless, a reservation should be considered for small organofluorine compounds, for which well-parameterized models for log P prediction are usually available.
Regarding the use of calculated molecular dipole moments as a descriptor of lipophilicity for small molecules, a more detailed analysis is required. Accordingly, a series of structurally simpler organofluorine compounds were retrieved (Figure 6), all from the same source [29], and a similar computational routine was carried out (see computational details section for a full description).
Figure 6: Chemical structure of the compounds 1–11 analyzed herein.
Figure 6: Chemical structure of the compounds 1–11 analyzed herein.
Compounds 7, 9, and 10 have the dependence of the molecular dipole moment μ with the rotation around the C–C bond. The correlation plots between the experimental log P of compounds 1–11 and a) dipole moment and b) predicted log P are shown in Figure 7.
![[1860-5397-16-200-7]](/bjoc/content/figures/1860-5397-16-200-7.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 7: Correlation between the experimental log P of compounds 1–11 and a) dipole moment (for 7, 9, and 10, μ is used as a weighted average of the gauche and anti-conformers), and b) predicted log P (milog P).
Figure 7: Correlation between the experimental log P of compounds 1–11 and a) dipole moment (for 7, 9, and 10...
From Figure 7a one can observe an r2 value of 0.53, which indicates a rough correlation between μ and log P. However, when applying the same hypothesis test, as for the first data set, a p-value of 0.0115 was obtained, which suggests that, although smaller than the first correlation, there is also a dependence between the calculated dipole moment and lipophilicity for small molecules. The considerably lower correlation may be explained by the fact that, in a small molecule, subtle structural changes strongly influence the overall molecular dipole and, sometimes, the introduction of a polar bond in a molecule decreases the overall molecular dipole moment. For instance, carbon tetrafluoride has four polar bonds, but it is apolar, while the other fluorinated methanes are all polar. Thus, the use of calculated molecular dipole moments as descriptors for lipophilicity in these small organofluorines should be used with caution. On the other hand, Figure 7b reveals a satisfactory correlation between the predicted and experimental values of log P, which reinforces that for simple molecules there are well-parameterized models for log P prediction, in spite of the remarkable systematic error.
Conclusion
In summary, the overall molecular polarity is influenced not only by the nature of the substituent group (as considered by additive techniques of prediction), but also by the orientation of the neat molecular dipole moment vector. In this sense, methods that ignore such influences result in reduced accuracy when predicting physicochemical properties of complex structures, such as the herbicides presented herein. Taking into account the correlation between lipophilicity and molecular conformation contributes to rationalize the effect of fluorine introduction on lipophilicity. Furthermore, the use of the molecular dipole moment that considers information on the molecular conformation, as presented herein, is a simple and straightforward parameter that can be valuable as a descriptor in quantitative structure–property relationships (QSPR). This could contribute significantly in studies involving organofluorine agrochemicals, for example, towards modeling herbicidal activity, and/or for environmental risk assessment.
Computational Details
The conformational search of agrochemicals I–VII was performed at the ωB97X-D/6-31G(d,p) [16,17] level of theory using the Spartan’18 software [30]. The lowest energy minimum conformation of each compound was then reoptimized and the dipole moment determined using a higher level of theory, ωB97X-D/6-311++G(d,p) [16,18], in the Gaussian 09 software [31]. The geometries and dipole moments for compounds 1–11 were calculated at the same level, which has been successfully applied to predict the conformational energies of other fluorine-containing compounds [32-34]. Frequency calculations were performed to confirm that the optimized geometries were true energy minima (no imaginary frequency) and to estimate thermodynamic energies, at 298.15 K. Solvent effects were accounted for by geometry optimization using the integral equation formalism variant of the polarizable continuum model (IEFPCM) [35]. Insights into the intramolecular interactions governing conformational preferences were obtained through the natural bond orbital (NBO) analysis [19,36]. The predicted log P was calculated using the Molinspiration Cheminformatics tool [25] and molecular structures were illustrated using CYLview [37].
Supporting Information
| Supporting Information File 1: Additional linear correlation, main conformers from the Monte Carlo conformational search, Cartesian coordinates and energies of the conformers of agrochemicals I–VII and compounds 1–11 analyzed herein. | ||
| Format: PDF | Size: 740.7 KB | Download |
Funding
The authors are grateful to the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, fellowship and scholarship grant numbers 301371/2017-2 and 140955/2017-8, respectively), the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES, funding code 001) and the Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG, grant number APQ-00383/15) for financial support.
References
-
Phillips, M. W. A. Pest Manage. Sci. 2020, 76, 3348–3356. doi:10.1002/ps.5728
Return to citation in text: [1] [2] -
Sparks, T. C.; Lorsbach, B. A. Pest Manage. Sci. 2017, 73, 672–677. doi:10.1002/ps.4457
Return to citation in text: [1] -
Jeffries, B.; Wang, Z.; Felstead, H. R.; Le Questel, J.-Y.; Scott, J. S.; Chiarparin, E.; Graton, J.; Linclau, B. J. Med. Chem. 2020, 63, 1002–1031. doi:10.1021/acs.jmedchem.9b01172
Return to citation in text: [1] -
Zhou, Y.; Wang, J.; Gu, Z.; Wang, S.; Zhu, W.; Aceña, J. L.; Soloshonok, V. A.; Izawa, K.; Liu, H. Chem. Rev. 2016, 116, 422–518. doi:10.1021/acs.chemrev.5b00392
Return to citation in text: [1] -
Fujiwara, T.; O’Hagan, D. J. Fluorine Chem. 2014, 167, 16–29. doi:10.1016/j.jfluchem.2014.06.014
Return to citation in text: [1] -
O’Hagan, D. J. Fluorine Chem. 2010, 131, 1071–1081. doi:10.1016/j.jfluchem.2010.03.003
Return to citation in text: [1] -
Gillis, E. P.; Eastman, K. J.; Hill, M. D.; Donnelly, D. J.; Meanwell, N. A. J. Med. Chem. 2015, 58, 8315–8359. doi:10.1021/acs.jmedchem.5b00258
Return to citation in text: [1] -
Hunter, L. Beilstein J. Org. Chem. 2010, 6, No. 38. doi:10.3762/bjoc.6.38
Return to citation in text: [1] -
Juaristi, E.; Notario, R. J. Org. Chem. 2016, 81, 1192–1197. doi:10.1021/acs.joc.5b02718
Return to citation in text: [1] [2] -
Keddie, N. S.; Slawin, A. M. Z.; Lebl, T.; Philp, D.; O'Hagan, D. Nat. Chem. 2015, 7, 483–488. doi:10.1038/nchem.2232
Return to citation in text: [1] [2] -
Müller, K. Chimia 2014, 68, 356–362. doi:10.2533/chimia.2014.356
Return to citation in text: [1] -
O'Hagan, D. Chem. Soc. Rev. 2008, 37, 308–319. doi:10.1039/b711844a
Return to citation in text: [1] -
O'Hagan, D.; Young, R. J. Angew. Chem., Int. Ed. 2016, 55, 3858–3860. doi:10.1002/anie.201511055
Angew. Chem. 2016, 128, 3922–3924. doi:10.1002/ange.201511055
Return to citation in text: [1] -
Buissonneaud, D. Y.; van Mourik, T.; O'Hagan, D. Tetrahedron 2010, 66, 2196–2202. doi:10.1016/j.tet.2010.01.049
Return to citation in text: [1] [2] -
Huchet, Q. A.; Kuhn, B.; Wagner, B.; Fischer, H.; Kansy, M.; Zimmerli, D.; Carreira, E. M.; Müller, K. J. Fluorine Chem. 2013, 152, 119–128. doi:10.1016/j.jfluchem.2013.02.023
Return to citation in text: [1] -
Chai, J.-D.; Head-Gordon, M. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. doi:10.1039/b810189b
Return to citation in text: [1] [2] [3] [4] -
Francl, M. M.; Pietro, W. J.; Hehre, W. J.; Binkley, J. S.; Gordon, M. S.; DeFrees, D. J.; Pople, J. A. J. Chem. Phys. 1982, 77, 3654–3665. doi:10.1063/1.444267
Return to citation in text: [1] [2] -
Krishnan, R.; Binkley, J. S.; Seeger, R.; Pople, J. A. J. Chem. Phys. 1980, 72, 650–654. doi:10.1063/1.438955
Return to citation in text: [1] [2] -
Glendening, E. D.; Landis, C. R.; Weinhold, F. J. Comput. Chem. 2013, 34, 1429–1437. doi:10.1002/jcc.23266
Return to citation in text: [1] [2] -
Goodman, L.; Gu, H.; Pophristic, V. J. Phys. Chem. A 2005, 109, 1223–1229. doi:10.1021/jp046290d
Return to citation in text: [1] -
Andrade, L. A. F.; Silla, J. M.; Duarte, C. J.; Rittner, R.; Freitas, M. P. Org. Biomol. Chem. 2013, 11, 6766–6771. doi:10.1039/c3ob41207e
Return to citation in text: [1] -
Silla, J. M.; Duarte, C. J.; Cormanich, R. A.; Rittner, R.; Freitas, M. P. Beilstein J. Org. Chem. 2014, 10, 877–882. doi:10.3762/bjoc.10.84
Return to citation in text: [1] -
Lonhienne, T.; Garcia, M. D.; Pierens, G.; Mobli, M.; Nouwens, A.; Guddat, L. W. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, E1945–E1954. doi:10.1073/pnas.1714392115
Return to citation in text: [1] -
SDS Finder – Dow Safety Data Sheets. https://www.dow.com/en-us/support/sds-finder.html.
Return to citation in text: [1] [2] -
Molinspiration Cheminformatics 2020; Calculation of Molecular Properties and Bioactivity Score. https://www.molinspiration.com/cgi-bin/properties.
Return to citation in text: [1] [2] [3] -
Carey, F.; Sundberg, R. Chemical Bonding and Molecular Structure. In Advanced Organic Chemistry: Part A: Structure and Mechanisms, 5th ed.; Springer: New York, NY, USA, 2008; p 52.
Return to citation in text: [1] -
Matter, H.; Barighaus, K.-H.; Naumann, T.; Klabunde, T.; Pirard, B. Comb. Chem. High Throughput Screening 2001, 4, 453–475. doi:10.2174/1386207013330896
Return to citation in text: [1] -
Mannhold, R.; van de Waterbeemd, H. J. Comput.-Aided Mol. Des. 2001, 15, 337–354. doi:10.1023/a:1011107422318
Return to citation in text: [1] -
Mackay, D.; Shiu, W.; Ma, K.-C.; Lee, S. Handbook of Physical-Chemical Properties and Environmental Fate for Organic Chemicals, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2006. doi:10.1201/9781420044393
Return to citation in text: [1] -
Spartan’18, Version 1.3.0; Wavefunction, Inc.: Irvine, CA, USA, 2018.
Return to citation in text: [1] -
Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, 2013.
Return to citation in text: [1] -
Silla, J. M.; Freitas, M. P. J. Fluorine Chem. 2019, 217, 8–12. doi:10.1016/j.jfluchem.2018.10.018
Return to citation in text: [1] -
Martins, F. A.; Silla, J. M.; Freitas, M. P. Beilstein J. Org. Chem. 2017, 13, 1781–1787. doi:10.3762/bjoc.13.172
Return to citation in text: [1] -
Andrade, L. A. F.; Freitas, M. P. New J. Chem. 2017, 41, 11672–11678. doi:10.1039/c7nj02463k
Return to citation in text: [1] -
Tomasi, J.; Mennucci, B.; Cammi, R. Chem. Rev. 2005, 105, 2999–3094. doi:10.1021/cr9904009
Return to citation in text: [1] -
NBO 6.0; Theoretical Chemistry Institute: University of Wisconsin, Madison, USA, 2013.
Return to citation in text: [1] -
CYLview, 1.0b; Legault, C. Y.: Université de Sherbrooke, 2009, http://www.cylview.org.
Return to citation in text: [1]
| 25. | Molinspiration Cheminformatics 2020; Calculation of Molecular Properties and Bioactivity Score. https://www.molinspiration.com/cgi-bin/properties. |
| 27. | Matter, H.; Barighaus, K.-H.; Naumann, T.; Klabunde, T.; Pirard, B. Comb. Chem. High Throughput Screening 2001, 4, 453–475. doi:10.2174/1386207013330896 |
| 28. | Mannhold, R.; van de Waterbeemd, H. J. Comput.-Aided Mol. Des. 2001, 15, 337–354. doi:10.1023/a:1011107422318 |
| 5. | Fujiwara, T.; O’Hagan, D. J. Fluorine Chem. 2014, 167, 16–29. doi:10.1016/j.jfluchem.2014.06.014 |
| 6. | O’Hagan, D. J. Fluorine Chem. 2010, 131, 1071–1081. doi:10.1016/j.jfluchem.2010.03.003 |
| 16. | Chai, J.-D.; Head-Gordon, M. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. doi:10.1039/b810189b |
| 17. | Francl, M. M.; Pietro, W. J.; Hehre, W. J.; Binkley, J. S.; Gordon, M. S.; DeFrees, D. J.; Pople, J. A. J. Chem. Phys. 1982, 77, 3654–3665. doi:10.1063/1.444267 |
| 35. | Tomasi, J.; Mennucci, B.; Cammi, R. Chem. Rev. 2005, 105, 2999–3094. doi:10.1021/cr9904009 |
| 3. | Jeffries, B.; Wang, Z.; Felstead, H. R.; Le Questel, J.-Y.; Scott, J. S.; Chiarparin, E.; Graton, J.; Linclau, B. J. Med. Chem. 2020, 63, 1002–1031. doi:10.1021/acs.jmedchem.9b01172 |
| 4. | Zhou, Y.; Wang, J.; Gu, Z.; Wang, S.; Zhu, W.; Aceña, J. L.; Soloshonok, V. A.; Izawa, K.; Liu, H. Chem. Rev. 2016, 116, 422–518. doi:10.1021/acs.chemrev.5b00392 |
| 16. | Chai, J.-D.; Head-Gordon, M. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. doi:10.1039/b810189b |
| 18. | Krishnan, R.; Binkley, J. S.; Seeger, R.; Pople, J. A. J. Chem. Phys. 1980, 72, 650–654. doi:10.1063/1.438955 |
| 19. | Glendening, E. D.; Landis, C. R.; Weinhold, F. J. Comput. Chem. 2013, 34, 1429–1437. doi:10.1002/jcc.23266 |
| 36. | NBO 6.0; Theoretical Chemistry Institute: University of Wisconsin, Madison, USA, 2013. |
| 2. | Sparks, T. C.; Lorsbach, B. A. Pest Manage. Sci. 2017, 73, 672–677. doi:10.1002/ps.4457 |
| 14. | Buissonneaud, D. Y.; van Mourik, T.; O'Hagan, D. Tetrahedron 2010, 66, 2196–2202. doi:10.1016/j.tet.2010.01.049 |
| 15. | Huchet, Q. A.; Kuhn, B.; Wagner, B.; Fischer, H.; Kansy, M.; Zimmerli, D.; Carreira, E. M.; Müller, K. J. Fluorine Chem. 2013, 152, 119–128. doi:10.1016/j.jfluchem.2013.02.023 |
| 32. | Silla, J. M.; Freitas, M. P. J. Fluorine Chem. 2019, 217, 8–12. doi:10.1016/j.jfluchem.2018.10.018 |
| 33. | Martins, F. A.; Silla, J. M.; Freitas, M. P. Beilstein J. Org. Chem. 2017, 13, 1781–1787. doi:10.3762/bjoc.13.172 |
| 34. | Andrade, L. A. F.; Freitas, M. P. New J. Chem. 2017, 41, 11672–11678. doi:10.1039/c7nj02463k |
| 10. | Keddie, N. S.; Slawin, A. M. Z.; Lebl, T.; Philp, D.; O'Hagan, D. Nat. Chem. 2015, 7, 483–488. doi:10.1038/nchem.2232 |
| 9. | Juaristi, E.; Notario, R. J. Org. Chem. 2016, 81, 1192–1197. doi:10.1021/acs.joc.5b02718 |
| 13. |
O'Hagan, D.; Young, R. J. Angew. Chem., Int. Ed. 2016, 55, 3858–3860. doi:10.1002/anie.201511055
Angew. Chem. 2016, 128, 3922–3924. doi:10.1002/ange.201511055 |
| 16. | Chai, J.-D.; Head-Gordon, M. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. doi:10.1039/b810189b |
| 18. | Krishnan, R.; Binkley, J. S.; Seeger, R.; Pople, J. A. J. Chem. Phys. 1980, 72, 650–654. doi:10.1063/1.438955 |
| 29. | Mackay, D.; Shiu, W.; Ma, K.-C.; Lee, S. Handbook of Physical-Chemical Properties and Environmental Fate for Organic Chemicals, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2006. doi:10.1201/9781420044393 |
| 7. | Gillis, E. P.; Eastman, K. J.; Hill, M. D.; Donnelly, D. J.; Meanwell, N. A. J. Med. Chem. 2015, 58, 8315–8359. doi:10.1021/acs.jmedchem.5b00258 |
| 16. | Chai, J.-D.; Head-Gordon, M. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. doi:10.1039/b810189b |
| 17. | Francl, M. M.; Pietro, W. J.; Hehre, W. J.; Binkley, J. S.; Gordon, M. S.; DeFrees, D. J.; Pople, J. A. J. Chem. Phys. 1982, 77, 3654–3665. doi:10.1063/1.444267 |
| 9. | Juaristi, E.; Notario, R. J. Org. Chem. 2016, 81, 1192–1197. doi:10.1021/acs.joc.5b02718 |
| 19. | Glendening, E. D.; Landis, C. R.; Weinhold, F. J. Comput. Chem. 2013, 34, 1429–1437. doi:10.1002/jcc.23266 |
| 25. | Molinspiration Cheminformatics 2020; Calculation of Molecular Properties and Bioactivity Score. https://www.molinspiration.com/cgi-bin/properties. |
| 14. | Buissonneaud, D. Y.; van Mourik, T.; O'Hagan, D. Tetrahedron 2010, 66, 2196–2202. doi:10.1016/j.tet.2010.01.049 |
| 20. | Goodman, L.; Gu, H.; Pophristic, V. J. Phys. Chem. A 2005, 109, 1223–1229. doi:10.1021/jp046290d |
| 37. | CYLview, 1.0b; Legault, C. Y.: Université de Sherbrooke, 2009, http://www.cylview.org. |
| 25. | Molinspiration Cheminformatics 2020; Calculation of Molecular Properties and Bioactivity Score. https://www.molinspiration.com/cgi-bin/properties. |
| 26. | Carey, F.; Sundberg, R. Chemical Bonding and Molecular Structure. In Advanced Organic Chemistry: Part A: Structure and Mechanisms, 5th ed.; Springer: New York, NY, USA, 2008; p 52. |
| 24. | SDS Finder – Dow Safety Data Sheets. https://www.dow.com/en-us/support/sds-finder.html. |
| 24. | SDS Finder – Dow Safety Data Sheets. https://www.dow.com/en-us/support/sds-finder.html. |
| 22. | Silla, J. M.; Duarte, C. J.; Cormanich, R. A.; Rittner, R.; Freitas, M. P. Beilstein J. Org. Chem. 2014, 10, 877–882. doi:10.3762/bjoc.10.84 |
| 23. | Lonhienne, T.; Garcia, M. D.; Pierens, G.; Mobli, M.; Nouwens, A.; Guddat, L. W. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, E1945–E1954. doi:10.1073/pnas.1714392115 |
| 10. | Keddie, N. S.; Slawin, A. M. Z.; Lebl, T.; Philp, D.; O'Hagan, D. Nat. Chem. 2015, 7, 483–488. doi:10.1038/nchem.2232 |
| 21. | Andrade, L. A. F.; Silla, J. M.; Duarte, C. J.; Rittner, R.; Freitas, M. P. Org. Biomol. Chem. 2013, 11, 6766–6771. doi:10.1039/c3ob41207e |
© 2020 Silva et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0). Please note that the reuse, redistribution and reproduction in particular requires that the authors and source are credited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (https://www.beilstein-journals.org/bjoc)