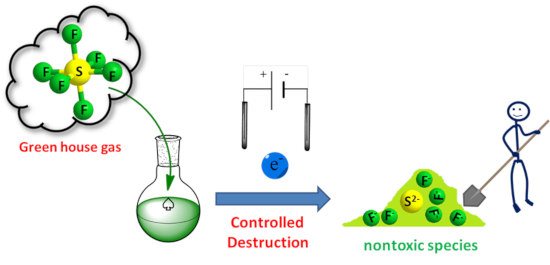
Abstract
The electroreduction of SF6 is shown at ambient temperature in acetonitrile using an array of platinum microelectrodes to improve the electrical detection. Its half reduction potential occurs at −2.17 V vs Fc+/Fc. The exact number of electrons for the full consumption of sulfur hexafluoride was determined and this gas further quantitatively transformed into environmentally benign fluoride anion and sulfur by electrochemical reduction.
Graphical Abstract
Introduction
Sulfur hexafluoride (SF6) is a fluorinated gas firstly identified in 1900 by Henry Moissan [1]. The strategy applied at industrial level to obtain SF6 uses sulfur in the presence of molecular fluorine. Sulfur hexafluoride possesses the particularity of being an inert gas both chemically and physiologically, it is non-flammable, has a high density and a high dielectric constant (2.5 times greater than that of air) [2-5]. These properties explain that this compound is widely used industrially as an electrical insulating gas in circuit breakers or in electrical substations [6,7]. On the other hand, SF6 is a greenhouse gas [8]. It has indeed a global warming potential (GWP) 22,000 times greater than CO2 [9]. From an industrial point of view, this requires efficient methods of recycling or destroying SF6. This last point implies, because of its great stability, the use of expensive methods requiring a large input of energy (high temperature, high pressure). Many SF6 decomposition strategies so far developed use photoreduction, plasma discharges or even photolysis processes [10,11]. Beyond the energetic high cost of such processes, they produce side products that are highly reactive, corrosive and toxic [12]. Recent and really impressive works were devoted to the decomposition of sulfur hexafluoride using stoichiometric or catalytic amounts of metals (Rh, Ni, Pt) [13-16]. Organic derivatives (phosphines or bipyridine) proved efficient tools for the selective degradation of SF6 [17,18]. Other elegant approaches have described the use of SF6 as precursor of reagent for fluorination or pentafluorosulfanylation. Very interestingly, the photochemical activation of this gas was described and allowed the in situ transformation of alcohols into alkyl fluorides [19,20]. The modern and green photoredox catalytic activation of SF6 was recently performed for the fluoro- and alkoxypentafluorosulfanylation of styrenes [21,22]. The same type of transformation was also described through the reductive activation of sulfur hexafluoride with TEMPO [23].
To the best of our knowledge, electrochemical reduction of SF6 has not yet been disclosed. The decomposition of sulfur hexafluoride by electrochemistry can nevertheless be a suitable answer and interesting alternative to the previous expensive options. In this article, we describe the electrochemical behavior of sulfur hexafluoride dissolved in various organic solvents. After combining an analytical approach of electrochemistry and 19F NMR spectroscopy, we have succeeded in the total consumption of SF6 in an electrochemical cell.
Results and Discussion
The first step of this work began with the measurement of the solubility of sulfur hexafluoride in an organic solvent. This data was not available in the literature but was however crucial for the implementation of the electrochemical experiences. Two solvents (DMF and acetonitrile) were selected for their good dissolution abilities and their large electroactivity area. The solubility of SF6 was measured, at 20 °C, by 19F NMR with chlorodifluoromethoxybenzene as internal standard probe. The concentration value for DMF was quite low (0.17 g/L) whereas the one for acetonitrile (2.48 g/L) was convenient for further studies. Acetonitrile is a common nonaqueous solvent in electrochemistry. Having a dielectric constant relatively high (ε = 38), acetonitrile allows a good dissociation of several salts providing the conductivity of the medium. The concentration of SF6 in the following studies was then around 1.7 × 10−2 M.
We then turned our attention to the determination of the reduction potential of SF6. To allow its electroreduction feasibility in acetonitrile, an electrochemical analytical approach was required [24]. This crucial step was supported by sensors which are based on a micro-disc-array of platinum ultramicroelectrodes (20 µm diameter) acting as multi-probe channels.
Due to their small size, microelectrodes provide electrochemical studies of very low concentrations of electroactive substances contained in a small amount of solvent. As a consequence, a conductive solvent is not required and a low concentration of conducting salt is sufficient. In contrast to macroelectrodes, the current density on microelectrodes is very high. This allows a better current sensitivity in electrochemical measurements (cyclic voltametrics, polarization curve …) providing the study of rapid electron and coupled chemical reactions. In comparison to macroelectrodes, their small size leads to a large decrease of the capacitive current and avoids IR drop effects. The array of Pt microdiscs offers the advantage of summing the current intensity of each microelectrode, thus increasing the sensitivity of the resulting current [25].
Whereas a planar diffusion is observed onto classical electrode (size >0.1 cm2), a hemispherical diffusion is expected with a microdisc electrode due to the contribution of the current diffusion by edge effects. The mass transport regime is then drastically modified on microdisc electrodes and can be adjusted in accordance with the polarization time by monitoring the potential scan rate. By cyclic voltametry, unlike macroelectrodes, the polarization of microelectrodes with a low potential scan rate (≤25 mV/s) leads to a drastic decrease of Cottrel contribution which involves the disappearance of current waves. The resulting current becomes a stationary current of diffusion (id), which is directly proportional to the bulk concentration of the electroactive substance (C∞), its diffusion coefficient in the solvent (D), the number of electrons exchanged in the electrochemical process (n), and the radius of the microelecrode (r) and F the Faraday constant, in accordance with the following relation [26]:
To the half limiting current (id/2) can be associated the half wave potential noted E1/2. For reversible electrons exchanged at the interface electrode/electrolyte, the half wave potential can be assimilated to the reversible formal potential redox couple noted E°ox/red [27]. After the addition of SF6, a stationary current is clearly observed before the acetonitrile reduction [28]. The electrochemial response of SF6 is related to a reproducible stationnary cathodic current. The intensity of the limiting current (plateau intensity) directly depends on SF6 concentration. From the voltamogram, the half wave potential of SF6 reduction is deduced and corresponds to −2.17 V vs Fc+/Fc (Figure 1).
![[1860-5397-16-244-1]](/bjoc/content/figures/1860-5397-16-244-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: (a) Cyclic voltammetry onto microelectrode arrays (Ø = 20 µm) in acetonitrile freshly distilled after the addition of TBAClO4 (0.1 M) at room temperature, under slight argon stream, v = 20 mV/s. (b) Same conditions as for (a) after addition of SF6. (c) Same conditions than (a) after addition of ferrocene (10−3 M).
Figure 1: (a) Cyclic voltammetry onto microelectrode arrays (Ø = 20 µm) in acetonitrile freshly distilled aft...
To the best of our knowledge, this was the first determination of the redox potential of sulfur hexafluoride. Pleasingly, this value was compatible with the employed solvent and offered the opportunity to reduce this gas in solution. In order to reach our target, i.e., the total consumption of SF6 into stable and nontoxic species, the next step was the determination of the number of electrons. It was determined by using two controlled size (S) of Pt electrodes: Pt ultramicroelectrode (∅ 20 µm, S1 = 3.14 × 10−6 cm2) and Pt macroelectrode (∅ 0.76 mm, S2 = 4.5 × 10−3 cm2). Using Pt ultramicroelectrode, the stationary current density (j1) is deduced from Equation 2:
Assuming a rapid electron transfer, the current (j2) decreases exponentially with time (t) according to the Cottrell law (Equation 3) onto a Pt macroelectrode, under sufficient electrochemical polarization [29].
From a combination of Equation 2 and Equation 3, the determination of the number of electrons exchanged is given by Equation 4 [30]:
The number of electrons exchanged (Equation 4) only depends on the validity of the Cottrell equation onto the macroelectrode (j2) since a constant current density (j1) is detected onto the microelectrode. The validity of the Cottrell equation requires a linear variation of the current density (j2) with t−1/2. This linear variation gives the upper limit on time. From this straight line the maximum duration (t) and the corresponding value of j2 are determined. These two values (t and j2) are then included in Equation 4 for the determination of the number of electrons exchanged. The macroelectrode (Ø = 0.76 mm) was polarized at −2.3 V vs Fc+/Fc after saturation of SF6 in the electrolyte. The chronoamperogram was reported in Figure 2. As it was expected, an exponential decrease of the current was indeed observed just before reaching a stationary current which was related to a constant layer thickness of SF6 diffusion. Indeed, the decrease in current comes from the consumption of SF6 at the interface electrode/acetonitrile. The current intensity depends on the SF6 flow in agreement with the 1st Fick’s Law from which the Cottrell equation is originated [29].
![[1860-5397-16-244-2]](/bjoc/content/figures/1860-5397-16-244-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Variation of the current reduction (i2) of SF6 onto Pt macroelectrode (Ø = 0.76 mm) at −2.3 V vs Fc+/Fc in acetonitrile freshly distilled after addition of TBAClO4 (0.1 M) at room temperature, under slight argon stream. Insert figure: Determination of the upper limit on time of Cottrell law from the straight line i2 = f(t−1/2).
Figure 2: Variation of the current reduction (i2) of SF6 onto Pt macroelectrode (Ø = 0.76 mm) at −2.3 V vs Fc+...
The upper limit on time was determined from the straight line reported in the insert figure (Figure 2). A value of 11.9 ± 0.7 s was deduced and the corresponding value of i2 (−34.2 µA ± 0.5) was determined from the chronoamperogram (Figure 2). Based on these values, the number of electron (ne− = 7.8 ± 0.3) was deduced from Equation 4. The reduction mechanism of SF6 can then involve 8 electrons per molecule:
This preliminary study is an important step to determine the best conditions for the SF6 electrolysis (the choice of potential polarization, the understanding of current decrease). With these analytical data in hands, the large scale decomposition of SF6 was then undertaken. The reactions were carried out in a single compartment with a conventional three-electrode arrangement: two platinum electrodes and one silver reference electrode, SRE (Figure 3). The electrolysis is performed at constant potential (−2.3 V vs Fc+/Fc) with a continuous supply of SF6 placed in a rubber balloon (constant bubbling).
![[1860-5397-16-244-3]](/bjoc/content/figures/1860-5397-16-244-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: Single compartment three-electrode experiment. 1: Balloon of SF6, 2: electrochemical cell, 3: reference electrode (silver wire), 4: counter-electrode (platinum), 5: working electrode (platinum).
Figure 3: Single compartment three-electrode experiment. 1: Balloon of SF6, 2: electrochemical cell, 3: refer...
The electrolysis was investigated on the same electrolyte but with larger surface of Pt electrode (15 cm2) (Figure 4). Figure 4b clearly highlights the consumption of the gas by the decrease of the electrochemical waves.
![[1860-5397-16-244-4]](/bjoc/content/figures/1860-5397-16-244-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: Electrolysis of SF6 at −2.3 V vs Fc+/Fc in acetonitrile freshly distilled after addition of TBAClO4 (0.1 M) at room temperature under slight argon stream. (a) Exponential decrease of the cathodic current according to the electrolysis duration onto a smooth Pt electrode (15 cm2). (b) Decrease of the cathodic current during the electrolysis duration which is detected onto an array of Pt microelectrodes (Ø = 20 µm).
Figure 4: Electrolysis of SF6 at −2.3 V vs Fc+/Fc in acetonitrile freshly distilled after addition of TBAClO4...
The control of the decomposition of the sulfur hexafluoride was also monitored by 19F NMR (Figure 5). After 3 hours experience, unidentified side-products were detected by NMR. Identification of these fleeting species as well as their potential reactivity are under current investigation in our laboratory. The left part of Figure 5 clearly demonstrates the total disappearance of SF6 after 6 hours as well as all the fluorinated organic compounds. The only peak detected by 19F NMR is around −153 ppm. This value corresponds to the classical chemical shift range of a fluoride anion. Due to its broad appearance, we can postulate the association with cations coming from the supporting electrolytes based on tetrabutylammonium (TBA) structures after anion exchange. This poor resolved signal is quite classical for such species due to hydrogen bonds. Another important point is the production of H+ ions at the counter electrode because of the oxidation of acetonitrile [31,32]:
They can associate themselves with the F− anions and generate bifluoride HF2 anions or even polyfluorides F(HF). The presence of fluoride anions can produce a Hoffman elimination on the alkyl chain of TBA giving rise to tributylamine, butene, and HF. We can suppose that the anion S2− could also be react with these hydrogen sources and become H2S. Nevertheless, in spite of our efforts it is very difficult to clearly identify all these decomposition compounds. A comprehensive analytical study could be of interest but it falls down the scope of the present article.
![[1860-5397-16-244-5]](/bjoc/content/figures/1860-5397-16-244-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: 19F NMR evolution of the crude mixture along the time after electrolysis realized at constant potential of −2.3 V/SRE; (left). 19F NMR expansion of the final mixture.
Figure 5: 19F NMR evolution of the crude mixture along the time after electrolysis realized at constant poten...
Conclusion
The smooth and controlled decomposition of sulfur hexafluoride was described under electroreduction. The reduction potential was firstly determined and used for preparative studies. The extrapolation on large scale of this methodology is under current development in our laboratory.
Experimental
Acetonitrile (HPLC grade, Mallinckrodt) was distilled from CaH2 and then degassed using three freeze-pump-thaw cycles before use. An electrochemical cell filled up with 40 mL of acetonitrile with TBABr (0.1 M) or TBAClO4 (0.1 M) as conducting salt at room temperature. The degassing of the medium was performed under an argon stream before the bubbling of SF6 to reach a saturated concentration that is 1.7 × 10−2 M. A balloon filled with 8 g of SF6 (0.055 mmol) is connected to the device (see Figure 3) and the electrolysis is carried out until the balloon is empty. The electrochemical set-up was a classical three electrodes device. All potentials were measured against a pseudo silver reference electrode (SRE). The addition of ferrocene in the electrolyte gives access to an internal reference [33]. In order to improve the current detection level of SF6, platinum disk electrodes were used as working electrode (Pt ultramicroelectrode with a diameter of 20 µm, an array of eight Pt ultramicroelectrodes with a diameter of 20 µm and a Pt macroelectrode with a diameter of 1 mm). Platinum disk microelectrodes were made by sealing into very fine glass, one or eight platinum wires, with a diameter of 20 µm, into the same soft glass tubing [33]. The microelectrodes array was polished successively on finer grades sand paper. After the analytical approach, a Pt wire (15 cm2) is used to allow SF6 electrolysis.
Whatever the step of the study (analytical, electrolysis) a smooth platinum electrode with a larger surface was used as a counter electrode. Electrochemical measurements were covered by a wide range of a potentiostat for more effective current detection. A potentiostat–galvanostat such as Princeton Applied Research Model 263 was monitored by its front panel and analogue-to-digital conversion was provided by «Powerlab». A Parstat 2273 potentiostat was also used with its internal «Powersuite» software. For all cyclic voltammetries, the conventional representation of anodic currents is reported as positive values and cathodic currents as negative values.
SF6 electrolysis was performed in acetonitrile with a constant potential in an undivided electrochemical cell.
The control of the decomposition of sulfur hexafluoride was monitored by 19F NMR. The spectra were recorded with a Bruker AC-200 or AC-300 spectrometer. Reported chemical shifts are based on a first order analysis. Internal reference was the peak of CFCl3 (δ = 0.00 ppm) for 19F (188 or 282 MHz) NMR spectra. The 19F NMR of the final mixture was recorded after concentration under vacuum to see a broad fluoride signal.
References
-
Moissan, H.; Lebeau, P. C. R. Hebd. Seances Acad. Sci. 1900, 130, 865–871.
Return to citation in text: [1] -
Weston, R. E. J. Phys. Chem. 1995, 99, 13150–13155. doi:10.1021/j100035a017
Return to citation in text: [1] -
Pola, J.; Engst, P.; Horák, M. Collect. Czech. Chem. Commun. 1979, 44, 2092–2095. doi:10.1135/cccc19792092
Return to citation in text: [1] -
Hagen, A. P.; Jones, D. J.; Ruttman, S. R. J. Inorg. Nucl. Chem. 1974, 36, 1217–1219. doi:10.1016/0022-1902(74)80054-0
Return to citation in text: [1] -
Case, J. R.; Nyman, F. Nature 1962, 193, 473. doi:10.1038/193473a0
Return to citation in text: [1] -
Naidu, M. S. Gas Insulated Substation; I.K. International: New Delhi, India, 2008.
Return to citation in text: [1] -
Christophorou, L. G.; Olthoff, J. K.; Van Brunt, R. J. IEEE Electr. Insul. Mag. 1997, 13, 20–24. doi:10.1109/57.620514
Return to citation in text: [1] -
Huang, L.; Shen, Y.; Dong, W.; Zhang, R.; Zhang, J.; Hou, H. J. Hazard. Mater. 2008, 151, 323–330. doi:10.1016/j.jhazmat.2007.05.080
Return to citation in text: [1] -
Maiss, M.; Brenninkmeijer, C. A. M. Environ. Sci. Technol. 1998, 32, 3077–3086. doi:10.1021/es9802807
Return to citation in text: [1] -
Totterdill, A.; Kovács, T.; Gómez Martín, J. C.; Feng, W.; Plane, J. M. C. J. Phys. Chem. A 2015, 119, 2016–2025. doi:10.1021/jp5123344
Return to citation in text: [1] -
Song, X.; Liu, X.; Ye, Z.; He, J.; Zhang, R.; Hou, H. J. Hazard. Mater. 2009, 168, 493–500. doi:10.1016/j.jhazmat.2009.02.047
Return to citation in text: [1] -
Tsai, W.-T. J. Fluorine Chem. 2007, 128, 1345–1352. doi:10.1016/j.jfluchem.2007.06.008
Return to citation in text: [1] -
Zámostná, L.; Braun, T.; Braun, B. Angew. Chem., Int. Ed. 2014, 53, 2745–2749. doi:10.1002/anie.201308254
Return to citation in text: [1] -
Holze, P.; Horn, B.; Limberg, C.; Matlachowski, C.; Mebs, S. Angew. Chem., Int. Ed. 2014, 53, 2750–2753. doi:10.1002/anie.201308270
Return to citation in text: [1] -
Zámostná, L.; Braun, T. Angew. Chem., Int. Ed. 2015, 54, 10652–10656. doi:10.1002/anie.201505462
Return to citation in text: [1] -
Berg, C.; Braun, T.; Ahrens, M.; Wittwer, P.; Herrmann, R. Angew. Chem., Int. Ed. 2017, 56, 4300–4304. doi:10.1002/anie.201612417
Return to citation in text: [1] -
Buß, F.; Mück-Lichtenfeld, C.; Mehlmann, P.; Dielmann, F. Angew. Chem., Int. Ed. 2018, 57, 4951–4955. doi:10.1002/anie.201713206
Return to citation in text: [1] -
Rueping, M.; Nikolaienko, P.; Lebedev, Y.; Adams, A. Green Chem. 2017, 19, 2571–2575. doi:10.1039/c7gc00877e
Return to citation in text: [1] -
McTeague, T. A.; Jamison, T. F. Angew. Chem., Int. Ed. 2016, 55, 15072–15075. doi:10.1002/anie.201608792
Return to citation in text: [1] -
Tomar, P.; Braun, T.; Kemnitz, E. Chem. Commun. 2018, 54, 9753–9756. doi:10.1039/c8cc05494k
Return to citation in text: [1] -
Rombach, D.; Wagenknecht, H.-A. ChemCatChem 2018, 10, 2955–2961. doi:10.1002/cctc.201800501
Return to citation in text: [1] -
Rombach, D.; Wagenknecht, H.-A. Angew. Chem., Int. Ed. 2020, 59, 300–303. doi:10.1002/anie.201910830
Return to citation in text: [1] -
Iakobson, G.; Pošta, M.; Beier, P. J. Fluorine Chem. 2018, 213, 51–55. doi:10.1016/j.jfluchem.2018.07.003
Return to citation in text: [1] -
Vedel, J.; Trémillon, B. J. Electroanal. Chem. (1959-1966) 1960, 1, 241–247. doi:10.1016/0022-0728(60)85018-8
Return to citation in text: [1] -
Montenegro, M. I.; Queiros, M. A.; Daschbach, J. L., Eds. Microelectrodes: Theory and Applications; Nato ASI Series. Series E: Applied Sciences 197; Springer Science + Business Media: Dordrecht, The Netherlands, 1991. doi:10.1007/978-94-011-3210-7
Return to citation in text: [1] -
Berionni, G.; Gonçalves, A.-M.; Mathieu, C.; Devic, T.; Etchéberry, A.; Goumont, R. Phys. Chem. Chem. Phys. 2011, 13, 2857–2869. doi:10.1039/c0cp01282c
Return to citation in text: [1] -
Jovené, C.; Jacquet, M.; Marrot, J.; Bourdreux, F.; Kletsky, M. E.; Burov, O. N.; Gonçalves, A.-M.; Goumont, R. Eur. J. Org. Chem. 2014, 6451–6466. doi:10.1002/ejoc.201402692
Return to citation in text: [1] -
Billon, J. P. J. Electroanal. Chem. (1959-1966) 1960, 1, 486–501. doi:10.1016/0022-0728(60)85295-3
Return to citation in text: [1] -
Bard, A. J.; Faulkner, L. R. Electrochimie Principes, méthodes et applications; Masson, 1983.
Return to citation in text: [1] [2] -
Amatore, C.; Azzabi, M.; Calas, P.; Jutand, A.; Lefrou, C.; Rollin, Y. J. Electroanal. Chem. Interfacial Electrochem. 1990, 288, 45–63. doi:10.1016/0022-0728(90)80024-z
Return to citation in text: [1] -
Vedel, J.; Trémillon, B. J. Electroanal. Chem. (1959-1966) 1960, 1, 241–247. doi:10.1016/0022-0728(60)85018-8
Return to citation in text: [1] -
Billon, J. P. J. Electroanal. Chem. (1959-1966) 1960, 1, 486–501. doi:10.1016/0022-0728(60)85295-3
Return to citation in text: [1] -
Gonçalves, A.-M.; Mathieu, C.; Herlem, M.; Etcheberry, A. J. Electroanal. Chem. 1999, 477, 140–145. doi:10.1016/s0022-0728(99)00398-8
Return to citation in text: [1] [2]
| 30. | Amatore, C.; Azzabi, M.; Calas, P.; Jutand, A.; Lefrou, C.; Rollin, Y. J. Electroanal. Chem. Interfacial Electrochem. 1990, 288, 45–63. doi:10.1016/0022-0728(90)80024-z |
| 28. | Billon, J. P. J. Electroanal. Chem. (1959-1966) 1960, 1, 486–501. doi:10.1016/0022-0728(60)85295-3 |
| 29. | Bard, A. J.; Faulkner, L. R. Electrochimie Principes, méthodes et applications; Masson, 1983. |
| 9. | Maiss, M.; Brenninkmeijer, C. A. M. Environ. Sci. Technol. 1998, 32, 3077–3086. doi:10.1021/es9802807 |
| 26. | Berionni, G.; Gonçalves, A.-M.; Mathieu, C.; Devic, T.; Etchéberry, A.; Goumont, R. Phys. Chem. Chem. Phys. 2011, 13, 2857–2869. doi:10.1039/c0cp01282c |
| 8. | Huang, L.; Shen, Y.; Dong, W.; Zhang, R.; Zhang, J.; Hou, H. J. Hazard. Mater. 2008, 151, 323–330. doi:10.1016/j.jhazmat.2007.05.080 |
| 27. | Jovené, C.; Jacquet, M.; Marrot, J.; Bourdreux, F.; Kletsky, M. E.; Burov, O. N.; Gonçalves, A.-M.; Goumont, R. Eur. J. Org. Chem. 2014, 6451–6466. doi:10.1002/ejoc.201402692 |
| 6. | Naidu, M. S. Gas Insulated Substation; I.K. International: New Delhi, India, 2008. |
| 7. | Christophorou, L. G.; Olthoff, J. K.; Van Brunt, R. J. IEEE Electr. Insul. Mag. 1997, 13, 20–24. doi:10.1109/57.620514 |
| 24. | Vedel, J.; Trémillon, B. J. Electroanal. Chem. (1959-1966) 1960, 1, 241–247. doi:10.1016/0022-0728(60)85018-8 |
| 2. | Weston, R. E. J. Phys. Chem. 1995, 99, 13150–13155. doi:10.1021/j100035a017 |
| 3. | Pola, J.; Engst, P.; Horák, M. Collect. Czech. Chem. Commun. 1979, 44, 2092–2095. doi:10.1135/cccc19792092 |
| 4. | Hagen, A. P.; Jones, D. J.; Ruttman, S. R. J. Inorg. Nucl. Chem. 1974, 36, 1217–1219. doi:10.1016/0022-1902(74)80054-0 |
| 5. | Case, J. R.; Nyman, F. Nature 1962, 193, 473. doi:10.1038/193473a0 |
| 25. | Montenegro, M. I.; Queiros, M. A.; Daschbach, J. L., Eds. Microelectrodes: Theory and Applications; Nato ASI Series. Series E: Applied Sciences 197; Springer Science + Business Media: Dordrecht, The Netherlands, 1991. doi:10.1007/978-94-011-3210-7 |
| 17. | Buß, F.; Mück-Lichtenfeld, C.; Mehlmann, P.; Dielmann, F. Angew. Chem., Int. Ed. 2018, 57, 4951–4955. doi:10.1002/anie.201713206 |
| 18. | Rueping, M.; Nikolaienko, P.; Lebedev, Y.; Adams, A. Green Chem. 2017, 19, 2571–2575. doi:10.1039/c7gc00877e |
| 21. | Rombach, D.; Wagenknecht, H.-A. ChemCatChem 2018, 10, 2955–2961. doi:10.1002/cctc.201800501 |
| 22. | Rombach, D.; Wagenknecht, H.-A. Angew. Chem., Int. Ed. 2020, 59, 300–303. doi:10.1002/anie.201910830 |
| 33. | Gonçalves, A.-M.; Mathieu, C.; Herlem, M.; Etcheberry, A. J. Electroanal. Chem. 1999, 477, 140–145. doi:10.1016/s0022-0728(99)00398-8 |
| 13. | Zámostná, L.; Braun, T.; Braun, B. Angew. Chem., Int. Ed. 2014, 53, 2745–2749. doi:10.1002/anie.201308254 |
| 14. | Holze, P.; Horn, B.; Limberg, C.; Matlachowski, C.; Mebs, S. Angew. Chem., Int. Ed. 2014, 53, 2750–2753. doi:10.1002/anie.201308270 |
| 15. | Zámostná, L.; Braun, T. Angew. Chem., Int. Ed. 2015, 54, 10652–10656. doi:10.1002/anie.201505462 |
| 16. | Berg, C.; Braun, T.; Ahrens, M.; Wittwer, P.; Herrmann, R. Angew. Chem., Int. Ed. 2017, 56, 4300–4304. doi:10.1002/anie.201612417 |
| 23. | Iakobson, G.; Pošta, M.; Beier, P. J. Fluorine Chem. 2018, 213, 51–55. doi:10.1016/j.jfluchem.2018.07.003 |
| 33. | Gonçalves, A.-M.; Mathieu, C.; Herlem, M.; Etcheberry, A. J. Electroanal. Chem. 1999, 477, 140–145. doi:10.1016/s0022-0728(99)00398-8 |
| 12. | Tsai, W.-T. J. Fluorine Chem. 2007, 128, 1345–1352. doi:10.1016/j.jfluchem.2007.06.008 |
| 29. | Bard, A. J.; Faulkner, L. R. Electrochimie Principes, méthodes et applications; Masson, 1983. |
| 10. | Totterdill, A.; Kovács, T.; Gómez Martín, J. C.; Feng, W.; Plane, J. M. C. J. Phys. Chem. A 2015, 119, 2016–2025. doi:10.1021/jp5123344 |
| 11. | Song, X.; Liu, X.; Ye, Z.; He, J.; Zhang, R.; Hou, H. J. Hazard. Mater. 2009, 168, 493–500. doi:10.1016/j.jhazmat.2009.02.047 |
| 19. | McTeague, T. A.; Jamison, T. F. Angew. Chem., Int. Ed. 2016, 55, 15072–15075. doi:10.1002/anie.201608792 |
| 20. | Tomar, P.; Braun, T.; Kemnitz, E. Chem. Commun. 2018, 54, 9753–9756. doi:10.1039/c8cc05494k |
| 31. | Vedel, J.; Trémillon, B. J. Electroanal. Chem. (1959-1966) 1960, 1, 241–247. doi:10.1016/0022-0728(60)85018-8 |
| 32. | Billon, J. P. J. Electroanal. Chem. (1959-1966) 1960, 1, 486–501. doi:10.1016/0022-0728(60)85295-3 |
© 2020 Bouvet et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0). Please note that the reuse, redistribution and reproduction in particular requires that the author(s) and source are credited and that individual graphics may be subject to special legal provisions.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (https://www.beilstein-journals.org/bjoc/terms)