Abstract
This paper reports the 1H, 13C and 15N NMR experimental study of five benzimidazoles in solution and in the solid state (13C and 15N CPMAS NMR) as well as the theoretically calculated (GIAO/DFT) chemical shifts. We have assigned unambiguously the "tautomeric positions" (C3a/C7a, C4/C7 and C5/C6) of NH-benzimidazoles that, in some solvents and in the solid state, appear different (blocked tautomerism). In the case of 1H-benzimidazole itself we have measured the prototropic rate in HMPA-d18.

Graphical Abstract
Introduction
Of almost any class of heterocycles it can be said that they have relevant biological and medicinal chemistry properties, because, for instance, over 80% of top small molecule drugs by US retail sales in 2010 contain at least one heterocyclic fragment in their structures [1]. Benzimidazoles besides being the skeleton of many relevant drugs (fungicides, anthelmintics, antiulcerative, antiviral,…) [2,3] are also part of some natural products (the most prominent benzimidazole compound in nature is N-ribosyl-5,6-dimethylbenzimidazole, which serves as an axial ligand for cobalt in vitamin B12) and have interesting ferroelectric properties [4]. Particularly relevant for the present work is their proton conducting abilities, based of the 1,3-N–H···N hydrogen bonds, not only in benzimidazole polymers but in molecular compounds [5,6].
Degenerated tautomerism (autotrope) [7,8] simultaneously simplifies and complicates the NMR spectra of molecules in solution to the point that the assignment of some signals that become magnetically equivalent (isochronous) [9,10] by fast proton exchange has been much neglected. With the advent of solid-state NMR spectroscopy and the suppression of prototropic tautomerism, the assignment problem arises anew. In recent years, the use of very pure NMR solvents, particularly DMSO-d6, and highfield instruments has lead to obtain solution spectra where the prototropy has been considerably slowed down.
We present in this paper a study of four N-unsubstituted 1H-benzimidazoles (Figure 1) including 2-methyl-1H-benzimidazole (2) that shows in the solid state ferroelectric switching in two dimensions due to its pseudo-tetragonal crystal symmetry [4], and 2-benzyl-1H-benzimidazole (4) a vessel-dilating and spasm-reducing agent known as dibazol or bendazole [3], where the tautomerism has been blocked resulting in the concomitant problem of assignment of some signals. We have selected 1-methyl-1H-benzimidazole (5) as the simplest benzimidazole without tautomerism.
The use of theoretically calculated chemical shifts has been decisive to solve this problem. We have used from 2001 [at the 6-31+G(d) level] [11] and then, from 2007, at the 6-311++G(d,p) level [12], a statistical approach that consists in comparing GIAO calculated absolute shieldings (σ, ppm) with experimental chemical shifts (δ) determined either in solution or in the solid state:
δ1H = 31.0 – 0.97 σ1H [13]
δ13C = 175.7 – 0.963 σ13C [12]
δ15N = –154.0 – 0.874 σ15N [12]
These equations give excellent results except for atoms (generally, carbon) linked to halogen atoms (I > Br > Cl >> F) [11,14] where relativistic corrections are necessary [15].
Results and Discussion
The experimental data are all original although averaged values of all nuclei have been reported for the three NH-benzimidazoles 1, 2 and 4 [16-21]; besides 13C and 15N NMR chemical shifts of 5 have been published [22,23].
Three kinds of calculations have been done: isolated molecules (gas phase), continuous model solvated molecules in DMSO, and hydrogen-bonded trimers for 1, to simulate the crystal [24]. The central benzimidazole is N–H···N hydrogen bonded to two other benzimidazoles like in the crystal chain (catemer). Two trimers, A and B, that differ in the conformation of the first benzimidazole were calculated for this compound, but the differences in energy are very small, less than 0.1 kJ·mol−1 (Figure 2).
![[1860-5397-10-168-2]](/bjoc/content/figures/1860-5397-10-168-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Trimers A (left) and B (right) of 1.
Figure 2: Trimers A (left) and B (right) of 1.
First, we will discuss the six carbon atoms of the benzene ring of benzimidazole (3a, 4, 5, 6, 7, 7a) and then the remaining atoms (N1, C2, N3 and those of the substituent). In NH-benzimidazoles, when prototropic tautomerism occurs (Figure 3), the signals of the benzimidazole carbons in groups of two coalesce in an average signal (the same happens with the N atoms but the chemical shifts are so different that there are no problems of assignment). Actually, this was a very common occurrence, but in the series of compounds of Table 1, only for benzimidazole itself and for 3, average signals were observed in DMSO-d6, a solvent known to slow down the prototropic exchanges. For these two compounds, we recorded the spectra in HMPA-d18, which is better for this purpose [25] observing the signals of compounds where the prototropic exchange is blocked.
Figure 3: The tautomerism of 1H-benzimidazole.
Figure 3: The tautomerism of 1H-benzimidazole.
Table 1: Calculated and experimental 1H and 13C chemical shifts of the benzene part.
| Compound |
1H calcd
gas |
1H calcd
DMSO |
1H exp.
HMPA-d18 273 K |
13C calcd
gas |
13C calcd
DMSO |
13C exp.
HMPA-d18 273 K |
13C exp.
CPMAS |
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 4 | 7.81 | 7.79 | 7.54 | 121.67 | 119.58 | 118.7 | 119.4 |
| 5 | 7.20 | 7.34 | 7.11 | 121.68 | 121.79 | 120.1 | 123.0 |
| 6 | 7.24 | 7.41 | 7.11 | 122.88 | 123.04 | 121.2 | 123.8 |
| 7 | 7.32 | 7.67 | 7.42 | 108.23 | 110.99 | 110.9 | 112.9 |
| 3a | – | – | – | 144.67 | 144.22 | 143.4 | 143.1 |
| 7a | – | – | – | 132.70 | 133.54 | 133.7 | 136.4 |
| 1 tri A | |||||||
| 4 | 7.89 | 7.93 | 7.54 | 119.85 | 118.28 | 118.7 | 119.4 |
| 5 | 7.26 | 7.39 | 7.11 | 122.10 | 121.91 | 120.1 | 123.0 |
| 6 | 7.28 | 7.39 | 7.11 | 122.93 | 122.73 | 121.2 | 123.8 |
| 7 | 7.49 | 7.77 | 7.42 | 110.00 | 111.88 | 110.9 | 112.9 |
| 3a | – | – | – | 143.85 | 143.62 | 143.4 | 143.1 |
| 7a | – | – | – | 134.13 | 134.76 | 133.7 | 136.4 |
| 1 tri B | |||||||
| 4 | 7.91 | 7.90 | 7.54 | 119.99 | 118.42 | 118.7 | 119.4 |
| 5 | 7.28 | 7.38 | 7.11 | 122.02 | 121.87 | 120.1 | 123.0 |
| 6 | 7.26 | 7.39 | 7.11 | 122.72 | 122.68 | 121.2 | 123.8 |
| 7 | 7.48 | 7.75 | 7.42 | 110.18 | 112.00 | 110.9 | 112.9 |
| 3a | – | – | – | 143.84 | 143.35 | 143.4 | 143.1 |
| 7a | – | – | – | 134.04 | 134.62 | 133.7 | 136.4 |
| Compound |
1H calcd
gas average |
1H calcd
DMSO average |
1H exp.
DMSO-d6 average |
13C calcd
gas average |
13C calcd
DMSO average |
13C exp.
DMSO-d6 average |
13C exp. CPMAS |
| 1 | |||||||
| 4/7 | 7.695 | 7.825 | 7.58 | 115.08 | 115.21 | 115.3 | |
| 5/6 | 7.27 | 7.385 | 7.17 | 122.37 | 122.28 | 121.7 | |
| 3a/7a | – | 138.94 | 138.98 | 138.4 | |||
| NH | 12.44 | ||||||
| 2 | |||||||
| 4 | 7.70 | 7.68 | 7.47 | 120.78 | 118.54 | 117.8 | 117.4 |
| 5 | 7.11 | 7.23 | 7.11 | 121.22 | 121.09 | 120.7 | 121.7 |
| 6 | 7.06 | 7.21 | 7.10 | 121.91 | 121.86 | 121.2 | 121.7 |
| 7 | 7.21 | 7.54 | 7.40 | 107.79 | 110.32 | 110.5 | 111.6 |
| 3a | – | – | – | 145.08 | 144.60 | 143.5 | 142.9 |
| 7a | – | – | – | 135.53 | 136.25 | 134.3 | 134.7 |
| NH | 12.14 | ||||||
| 3 |
1H calcd
gas |
1H calcd
DMSO |
1H exp.
HMPA-d18 273 K |
13C calcd
gas |
13C calcd
DMSO |
13C exp.
HMPA-d18 273 K |
13C exp. CPMAS |
| 4 | 7.87 | 7.88 | 7.72 | 122.65 | 120.89 | 120.8 |
114.7
118.0 |
| 5 | 7.43 | 7.59 | 7.37 | 124.08 | 124.84 | 123.2 |
120.3
122.1 |
| 6 | 7.37 | 7.57 | 7.42 | 125.89 | 126.68 | 125.1 |
128.1
130.7 |
| 7 | 7.31 | 7.67 | 7.58 | 109.07 | 112.00 | 112.9 |
108.2
109.3 |
| 3a | – | – | – | 144.54 | 143.87 | 142.9 | |
| 7a | – | – | – | 132.27 | 133.24 | 135.1 | |
| NH | 15.05 | ||||||
| 4 |
1H calcd
gas |
1H calcd
DMSO |
1H exp.
DMSO-d6 |
13C calcd
gas |
13C calcd
DMSO |
13C exp.
DMSO-d6 |
13C exp. CPMAS |
| 4 | 7.74 | 7.70 | 7.52 | 120.46 | 118.51 | 118.3 | 120.2 |
| 5 | 7.27 | 7.38 | 7.10 | 121.91 | 122.22 | 120.9 | 123.0 |
| 6 | 7.12 | 7.28 | 7.11 | 122.64 | 122.79 | 121.6 | 124.8 |
| 7 | 6.95 | 7.32 | 7.40 | 107.24 | 109.79 | 110.9 | 113.5 |
| 3a | – | – | – | 144.14 | 143.43 | 143.4 | 143.0 |
| 7a | – | – | – | 134.27 | 135.43 | 134.3 | 135.2 |
| NH | 12.28 | ||||||
| 5 |
1H calcd
gas |
1H calcd
DMSO |
1H exp.
DMSO-d6 |
13C calcd
gas |
13C calcd
DMSO |
13C exp.
DMSO-d6 |
13C exp. CPMAS |
| 4 | 7.80 | 7.77 | 7.64a | 121.81 | 119.62 | 119.2 | 119.1 |
| 5 | 7.23 | 7.36 | 7.19a | 121.55 | 121.73 | 121.3 | 121.2 |
| 6 | 7.20 | 7.36 | 7.25a | 122.32 | 122.53 | 122.1 | 123.2 |
| 7 | 7.24 | 7.59 | 7.54a | 106.50 | 109.36 | 110.1 | 110.7 |
| 3a | – | – | – | 146.49 | 145.60 | 143.3 | 143.4 |
| 7a | – | – | – | 135.58 | 136.21 | 134.5 | 134.7 |
a 3J45 = 7.89, 4J46 = 1.26, 5J47 = 0.78, 3J56 = 7.14, 4J57 = 1.30, 3J67 = 7.99 Hz.
The assignment of the signals of Table 1, Table 2 and Table 3 was straightforward following these steps: i) A NOESY experiment identifies H7 (7.54 ppm) of 5 by its proximity to the N-methyl group; ii) the analysis of the ABCD system of the protons H4, H5, H6 and H7, identifies the remaining protons; iii) a series of 2D experiments assign the CH carbons (HMQC) as well as the quaternary carbons C3a and C7a (HMBC).
Table 2: Calculated and experimental 13C chemical shifts of the imidazole and substituent parts.
| Compound |
1H calcd
gas |
1H calcd
DMSO |
1H exp.
HMPA-d18 |
13C calcd
gas |
13C calcd
DMSO |
13C exp.
HMPA-d18 |
13C exp. CPMAS |
|---|---|---|---|---|---|---|---|
| 1 | |||||||
| 2 | 7.64 | 7.95 | 8.21 | 136.78 | 140.77 | 141.6 | 143.1 |
| 1 tri A | |||||||
| 2 | 8.01 | 8.32 | 8.21 | 139.05 | 141.86 | 141.6 | 143.1 |
| 1 tri B | |||||||
| 2 | 7.95 | 8.24 | 8.21 | 138.24 | 141.16 | 141.6 | 143.1 |
| Compound |
1H calcd
gas |
1H calcd
DMSO |
1H exp.
DMSO-d6 |
13C calcd
gas |
13C calcd
DMSO |
13C exp.
DMSO-d6 |
13C exp. CPMAS |
| 1 | |||||||
| 2 | 8.20 | 141.9 | |||||
| 2 | |||||||
| 2 | – | – | – | 146.54 | 151.70 | 151.2 | 153.6 |
| Me | 2.41 | 2.50 | 2.47 | 14.37 | 14.42 | 14.6 | 12.6 |
|
13C exp
HMPA-d18 |
|||||||
| 3a,b | |||||||
| 2 | – | – | – | 138.96 | 139.54 |
140.8
2JCF = 39.1 |
135.2
137.8 |
| CF3 | – | – | – | 123.53 | 123.96 |
120.0
1JCF = 270.1 |
116.0 |
| 4 | |||||||
| 2 | – | – | – | 151.48 | 155.02 | 153.5 | 157.1 |
| CH2 | 4.18 | 4.22 | 35.0 | 38.73 | 38.42 | 35.0 | 36.0 |
| Cipso | – | – | – | 139.73 | 139.83 | 137.7 | 136.2 |
| Cortho | 7.30 | 7.54 | 7.30 | 129.32 | 129.28 | 128.5 | ~127 |
| Cmeta | 7.38 | 7.49 | 7.33 | 128.76 | 129.44 | 128.8 | ~127 |
| Cpara | 7.34 | 7.38 | 7.22 | 126.76 | 127.15 | 126.5 | 124.3 |
| 5 | |||||||
| 2 | 7.41 | 7.74 | 8.16c | 140.83 | 144.14 | 144.5 | 144.6 |
| NMe | 3.62 | 3.80 | 3.82c | 29.78 | 30.69 | 30.6 | 29.7 |
aIn HMPA-d18 273 K; b 19F calc.: −63.35 (gas), −63.84 (DMSO); 19F exp.: −62.8 (HMPA-d18); −61.2 (CPMAS). c 4JHMe = 0.42 Hz.
Table 3: Calculated and experimental 15N chemical shifts of the imidazole part.
| Compound | 15N calcd gas | 15N calcd DMSO | 15N exp. HMPA-d18 | 15N exp. CPMAS |
|---|---|---|---|---|
| 1 | ||||
| N1 | −247.63 | −240.09 | −228.4 | −221.8 |
| N3 | −125.53 | −140.75 | −134.0 | −143.9 |
| 1 tri A | ||||
| N1 | −227.89 | −222.08 | −228.4 | −221.8 |
| N3 | −142.23 | −149.24 | −134.0 | −143.9 |
| 1 tri B | ||||
| N1 | −227.80 | −221.92 | −228.4 | −221.8 |
| N3 | −142.21 | −149.18 | −134.0 | −143.9 |
| Compound |
15N calcd gas
average |
15N calcd DMSO
average |
15N exp. DMSO-d6
average |
15N exp. CPMAS |
| 1 | ||||
| N1/N3 | −186.58 | −190.42 | a | |
| 2 | ||||
| N1 | −246.87 | −240.39 | −230.3 | −219.5, −224.2 |
| N3 | −127.73 | −142.15 | −137.9 | −146.9 |
| 15N exp HMPA-d18 | ||||
| 3b | ||||
| N1 | −247.40 | −241.51 | −230.4 | −225.9 |
| N3 | −120.36 | −132.07 | a | −142.8 |
| 4 | ||||
| N1 | −245.40 | −241.11 | −230.8 | −221.8 |
| N3 | −130.39 | −141.51 | −136.6 | −147.2 |
| 5 | ||||
| N1 | −241.25 | −232.11 | −235.6 | −233.4 |
| N3 | −128.38 | −143.76 | −136.4 | −135.4 |
aNot observed; bIn HMPA-d18 273 K.
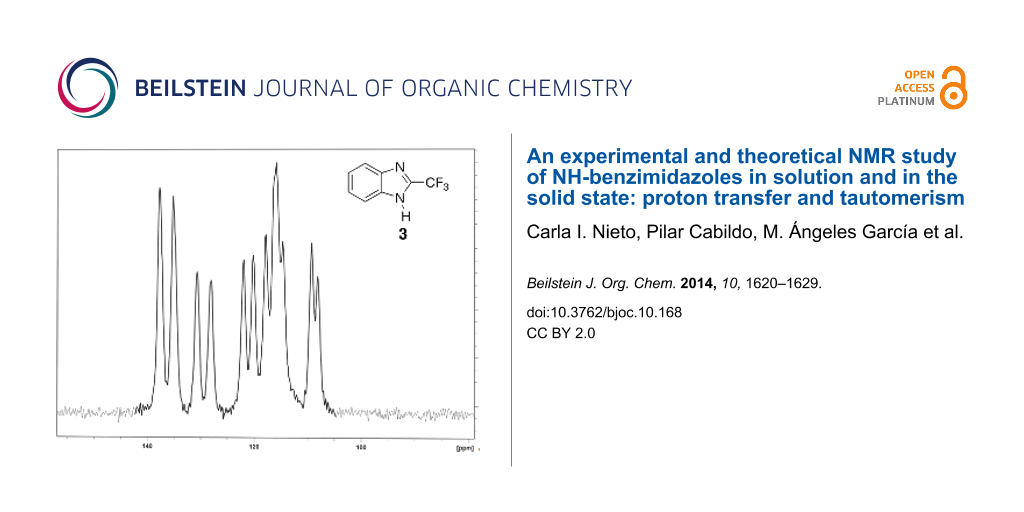
In the case of 3 all signals are considerably split in the solid state (Figure 4).
![[1860-5397-10-168-4]](/bjoc/content/figures/1860-5397-10-168-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: The 13C CPMAS NMR spectrum of 3.
Figure 4: The 13C CPMAS NMR spectrum of 3.
The X-ray structure of compound 3 is known and reported in the Cambridge Structural Database (refcode: ZAQRIU01) [4,26]. There are two independent molecules and in one of them, the CF3 is disordered (Figure 5). The most probable explanation of the splittings of Figure 4 is the existence of two independent molecules, a fact that is well documented in the literature [27-30].
![[1860-5397-10-168-5]](/bjoc/content/figures/1860-5397-10-168-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: The two independent molecules of 3 drawn with the Mercury program [26].
Figure 5: The two independent molecules of 3 drawn with the Mercury program [26].
We have collected in Table 4 the different equations obtained from the data of Table 1, Table 2 and Table 3.
Table 4: Linear regression equations, intercepts in ppm. If not specified, both trimers yield the same results.
| Eq. | No | Intercept | Slope | R2 | Atom | Exp. | Calcd |
|---|---|---|---|---|---|---|---|
| 1 | 26 | (3.2 ± 0.7) | (0.55 ± 0.10) | 0.563 | 1H | solution | gas phase |
| 2 | 26 | (1.2 ± 0.6) | (0.81 ± 0.08) | 0.797 | 1H | solution | DMSO |
| 3 | 59 | −(0.2 ± 1.3) | (1.00 ± 0.01) | 0.993 | 13C | solution | gas phase |
| 4 | 59 | −(0.7 ± 0.7) | (1.000 ± 0.001) | 0.998 | 13C | solution | DMSO |
| 5 | 59 | −(0.7 ± 2.0) | (1.01 ± 0.02) | 0.987 | 13C | CPMAS | gas phase |
| 6 | 59 | −(0.8 ± 1.2) | (1.01 ± 0.01) | 0.993 | 13C | CPMAS | DMSO |
| 7a | 58 | −(0.2 ± 1.3) | (1.00 ± 0.01) | 0.994 | 13C | solution | gas phase |
| 8a | 58 | −(0.7 ± 0.7) | (1.000 ± 0.005) | 0.998 | 13C | solution | DMSO |
| 9a | 53 | −(0.6 ± 1.9) | (1.01 ± 0.02) | 0.989 | 13C | CPMAS | gas phase |
| 10a | 53 | −(1.1 ± 1.3) | (1.01 ± 0.01) | 0.995 | 13C | CPMAS | DMSO |
| 11 | 6 | (6.6 ± 7.2) | (0.95 ± 0.06) | 0.986 | 13C | CPMAS | monomerb |
| 12 | 6 | (5.2 ± 3.3) | (0.96 ± 0.03) | 0.997 | 13C | CPMAS | trimer Ab |
| 13 | 6 | (3.7 ± 3.4) | (0.98 ± 0.03) | 0.997 | 13C | CPMAS | trimer Bb |
| 14 | 14 | −(22.3 ± 7.3) | (0.86 ± 0.04) | 0.978 | 15N | solution | gas |
| 15 | 14 | (10.5 ± 9.1) | (1.02 ± 0.05) | 0.976 | 15N | solution | DMSO |
| 16 | 14 | −(51.0 ± 7.1) | (0.72 ± 0.04) | 0.970 | 15N | CPMAS | gas |
| 17 | 14 | −(23.5 ± 7.5) | (0.86 ± 0.04) | 0.976 | 15N | CPMAS | DMSO |
| 18 | 10 | −(1.4 ± 6.6) | (0.96 ± 0.03) | 0.991 | 15N | solution | monomerb |
| 19 | 10 | (6.6 ± 10.4) | (1.00 ± 0.05) | 0.979 | 15N | solution | trimerb |
| 20 | 10 | −(29.8 ± 5.3) | (0.82 ± 0.03) | 0.991 | 15N | CPMAS | monomerb |
| 21 | 10 | −(23.8 ± 7.5) | (0.85 ± 0.04) | 0.984 | 15N | CPMAS | trimerb |
aThe 13C signal of the CF3 group has been removed. bDMSO calculations.
i) The 1H chemical shifts are much more consistent with calculations for DMSO as solvent than with those of isolated molecules (gas phase). For 26 points, the R2 coefficient increases from 0.56 (eq. 1) to 0.80 (eq. 2). The use of the monomer or the central part of the trimer has no influence. The worse point is H7 of 4 that appears at 7.40 ppm and fitted with eq. 2 has a value of 7.14 ppm. The origin of this discrepancy is that the theoretical conformation corresponding to the X-ray structure is not stable and reverts to the minimum one, which has the benzyl group rotated.
ii) The 13C chemical shifts (eqs. 3–13) are very well reproduced by the calculations: high R2 values, small intercepts (in several cases, not significant) and slopes close to 1. Systematically, the worse point was the carbon atom of the CF3 substituent (halogen substituents produce effects that are not well reproduced by our calculations that not include relativistic corrections) [15], removing it does not significantly modify the regression values (compare eqs. 3–6 with eqs. 7–10). CPMAS values agree better with calculations including DMSO solvent effect (compare eqs. 9 and 10) and also better with trimer B (in turn, slightly better than with trimer A, compare intercept and slopes of eqs. 12 and 13) than with the monomer (eq. 11).
iii) Concerning 15N NMR (eqs. 14–21), the R2 values are lower than with 13C NMR. Both for solution and for CPMAS, the gas phase and DMSO calculations are comparable in terms of R2 (eqs. 14–17), however, the values of the slopes (the closer to 1, the better) and intercepts (the closer to 0, the better), clearly favored the DMSO calculations. Surprisingly, the monomer appears preferable to the trimer (eqs. 18,19 and 20,21) which is understandable for the solution but not for the solid state. More complex approaches, such as periodic calculations [31], are necessary.
Influence of the substituent at position 2 on the tautomerization rate
We have observed a different behavior for the four NH-benzimidazoles: 1 and 3 yielded average signals in DMSO-d6 and only in HMPA-d18 the prototropic exchange was slow, on the other hand 2 and 4 behaved as if the tautomerism was blocked in DMSO-d6. In the case of 1 a dynamic NMR (DNMR) study in HMPA-d18 was performed (Figure 6).
![[1860-5397-10-168-6]](/bjoc/content/figures/1860-5397-10-168-6.png?scale=1.4&max-width=1024&background=FFFFFF)
Figure 6: The evolution of the spectrum of 1 with temperature in HMPA-d18.
Figure 6: The evolution of the spectrum of 1 with temperature in HMPA-d18.
The relevant data are: TC = 277.5 K and Δν = 0.12 ppm = 48 Hz; from them and using the Eyring equation [ΔG‡TC = 19.12 × TC × (10.32 + log TC/kC)] [32], we obtained: kC = 67.88 s−1 and ΔG‡277.5 = 58.0 kJ·mol−1. This barrier is similar to that of pyrazole in the same solvent (58.6 kJ·mol−1 at 289 K) [33].
The effect of the substituent at position 2 on the rate (roughly, CF3 and H, fast; CH2C6H5 and CH3, slow) is probably the consequence of steric and electronic effects; many years ago, we showed that intramolecular hydrogen bonds also affect the rate [34]. The calculated electrostatic potential minima associated to the lone pair of the N3 follow the tautomerization rate ranking of the molecules (−0.085 au, CF3, −0.103, H, −0.104, CH2C6H5 and −0.105, CH3).
Conclusion
The data reported here for NH-benzimidazoles when the prototropy is blocked should be useful to determine the tautomeric composition when there are substituents at positions 4(7) or 5(6), for instance, in the case of omeprazole, a 5(6)-methoxy-1H-benzimidazole derivative [35,36]. Besides, solid state results as well as GIAO calculations provide new data to characterize this important family of compounds. Finally, by means of DNMR experiments it was possible to determine the barrier to proton transfer of benzimidazole itself in HMPA-d18, thus providing a missing value in heterocyclic tautomerism of azoles and benzazoles [33].
Experimental
Four of the compounds reported in this paper are commercial (Sigma-Aldrich): 1, 2, 3 and 5. We reported the synthesis of the fifth one, 4, in [37].
NMR spectroscopy
Solution NMR spectra were recorded on a Bruker DRX 400 (9.4 Tesla, 400.13 MHz for 1H, 100.62 MHz for 13C and 40.54 MHz for 15N) spectrometer with a 5 mm inverse-detection H-X probe equipped with a z-gradient coil, at 300 K. Chemical shifts (δ) are given from internal solvent, DMSO-d6 2.49 for 1H and 39.5 for 13C. Typical parameters for 1H NMR spectra were spectral width 4800 Hz and pulse width 8.3 μs at an attenuation level of 0 dB. Typical parameters for 13C NMR spectra were spectral width 21 kHz, pulse width 12.5 μs at an attenuation level of −6 dB and relaxation delay 2s, WALTZ-16 was used for broadband proton decoupling; the FIDS were multiplied by an exponential weighting (lb = 1Hz) before Fourier transformation.
Inverse proton detected heteronuclear shift correlation spectra, (1H,13C) gs-HMQC and (1H,13C) gs-HMBC, were acquired and processed using standard Bruker NMR software and in nonphase-sensitive mode. Gradient selection was achieved through a 5% sine truncated shaped pulse gradient of 1 ms.
Selected parameters for (1H,13C) gs-HMQC and (1H,13C) gs-HMBC spectra were spectral width 4800 Hz for 1H and 20.5 kHz for 13C, 1024 × 256 data set, number of scans 2 (gs-HMQC) or 4 (gs-HMBC) and relaxation delay 1s. The FIDs were processed using zero filling in the F1 domain and a sine-bell window function in both dimensions was applied prior to Fourier transformation. In the gs-HMQC experiments, GARP modulation of 13C was used for decoupling.
Selected parameters for (1H,15N) gs-HMQC and (1H,15N) gs-HMBC spectra were spectral width 3500 Hz for 1H and 12.5 kHz for 15N, 1024 × 256 data set, number of scans 4, relaxation delay 1s, 37–60 ms delay for evolution of the 15N,1H long-range coupling. The FIDs were processed using zero filling in the F1 domain and a sine-bell window function in both dimensions was applied prior to Fourier transformation.
For 19F NMR (379.50 MHz) a 5 mm QNP direct-detection probehead equipped with a z-gradient coil, at 300 K was required.
Chemical shifts (δ) are given from internal solvent, DMSO-d6 2.49 and HMPA-d18 2.57 for 1H; 39.5 and 35.8 for 13C, and for 15N and 19F NMR, nitromethane (0.00) and one drop of CFCl3 in CDCl3 (0.00) were used as external references
Typical parameters for 1H NMR were: spectral width 4800 Hz and pulse width 10.25 μs at an attenuation level of −3.0 dB. For 13C NMR: spectral width 21 kHz, pulse width 8.75 μs at an attenuation level of −3 dB and relaxation delay 2 s, WALTZ-16 was used for broadband proton decoupling; the FIDS were multiplied by an exponential weighting (lb = 1Hz) before Fourier transformation. For 19F NMR: spectral width 55 kHz, pulse width 13.57 μs at an attenuation level of −6 dB and relaxation delay 1s.
Variable temperature: A Bruker BVT3000 temperature unit was used to control the temperature of the cooling gas stream and an exchanger to achive low temperatures. To avoid problems at low temperatures caused by air moisture, pure nitrogen was used as bearing, driving and cooling gas. When not stated explicitly, the temperature was 293 K.
We have always used a 1.4 M solution of the compounds either in DMSO-d6 or in HMPA-d18; this corresponds, in the case of 1, to 10 mg in 0.6 mL. To avoid water contamination, a new sealed ampoule was open for each experiment.
Solid state 13C (100.73 MHz) and 15N (40.60 MHz) CPMAS NMR spectra were obtained on a Bruker WB 400 spectrometer at 300 K using a 4 mm DVT probehead. Samples were carefully packed in 4 mm diameter cylindrical zirconia rotors with Kel-F end-caps. Operating conditions involved 2.9 µs 90° 1H pulses and decoupling field strength of 86.2 kHz by TPPM sequence. 13C spectra were originally referenced to a glycine sample and then the chemical shifts were recalculated to the Me4Si [for the carbonyl atom δ (glycine) = 176.1] and 15N spectra to 15NH4Cl and then converted to nitromethane scale using the relationship: δ 15N(nitromethane) = δ1 5N(ammonium chloride) − 338.1.
Typical acquisition parameters for 13C CPMAS were: spectral width, 40 kHz; recycle delay, 5–60 s; acquisition time, 30 ms; contact time, 2–4 ms; and spin rate, 12 kHz. In order to distinguish protonated and non-protonated carbon atoms, the NQS (Non-Quaternary Suppression) experiment by conventional cross-polarization was recorded; before the acquisition the decoupler is switched off for a very short time of 25 μs [38-40]. For 15N CPMAS were: spectral width, 40 kHz; recycle delay, 5–60 s; acquisition time, 35 ms; contact time, 7–9 ms; and spin rate, 6 kHz.
Solid state 19F (376.94 MHz) NMR spectra were obtained on a Bruker WB 400 spectrometer using a MAS DVT BL2.5 X/F/H probe. Samples were carefully packed in 2.5 mm diameter cylindrical zirconia rotors with Kel-F end-caps.
Typical acquisition parameters 19F{1H} MAS were: spectral width, 75 kHz; recycle delay, 10 s; pulse width, 2.5 μs and proton decoupling field strength of 100 kHz by SPINAL-64 sequence; recycle delay, 10 s; acquisition time, 25 ms; 128 scans; and spin rate, 25 kHz. The 19F spectra was referenced to ammonium trifluoroacetate sample and then the chemical shifts were recalculated to the CFCl3 [δ (CF3CO2NH4+) = −72.0].
Computational details
Using the Gaussian 09 facilities [41], GIAO [42,43]/B3LYP [44-46]/6-311++G(d,p) [47,48] calculations were carried out; DMSO effects were calculated using the PCM continuum model [49] also with the Gaussian 09 series of programs.
Supporting Information
| Supporting Information File 1: Optimized geometry of the systems, and chemical shifts in gas phase and PCM/DMSO environment. | ||
| Format: PDF | Size: 93.1 KB | Download |
Acknowledgements
This work has been financed by Ministerio de Ciencia e Innovación (CTQ2010-16122) and Ministerio de Economía y Competitividad of Spain (CTQ2012-35513-C02-02) and Comunidad Autónoma de Madrid (Project MADRISOLAR2, ref. S2009/PPQ-1533). One of us (C. I. Nieto) is indebted to UNED for a predoctoral fellowship (FPI “Grupos de Investigación” UNED).
References
-
Gomtsyan, A. Chem. Heterocycl. Compd. 2012, 48, 7–10. doi:10.1007/s10593-012-0960-z
Return to citation in text: [1] -
Velík, J.; Baliharová, V.; Fink-Gremmels, J.; Bull, S.; Lamka, J.; Skálová, L. Res. Vet. Sci. 2004, 76, 95–108. doi:10.1016/j.rvsc.2003.08.005
Return to citation in text: [1] -
Khokra, S. L.; Choudhary, D. Asian J. Biochem. Pharm. Res. 2011, 1, 476–486.
Return to citation in text: [1] [2] -
Horiuchi, S.; Kagawa, F.; Hatahara, K.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Nat. Commun. 2012, 3, No. 1308. doi:10.1038/ncomms2322
Return to citation in text: [1] [2] [3] -
Pogorzelec-Glaser, K.; Rachocki, A.; Ławniczak, P.; Pietraszko, A.; Pawlaczyk, C.; Hilczer, B.; Pugaczowa-Michalska, M. CrystEngComm 2013, 15, 1950–1959. doi:10.1039/c2ce26571k
Return to citation in text: [1] -
Rachocki, A.; Pogorzelec-Glaser, K.; Ławniczak, P.; Pugaczowa-Michalska, M.; Łapinski, A.; Hilczer, B.; Matczak, M.; Pietraszko, A. Cryst. Growth Des. 2014, 14, 1211–1220. doi:10.1021/cg401742b
Return to citation in text: [1] -
Elguero, J.; Katritzky, A. R.; Denisko, O. V. Adv. Heterocycl. Chem. 2000, 76, 1–84. doi:10.1016/S0065-2725(00)76003-X
Return to citation in text: [1] -
Alkorta, I.; Elguero, J. Top. Heterocycl. Chem. 2008, 19, 155–202.
Return to citation in text: [1] -
Weber, U.; Thiele, H. NMR Spectroscopy: Modern Spectral Analysis,; Wiley-VCH: Weinheim, 1998.
Return to citation in text: [1] -
Simpson, J. H. Organic Structure Determination using 2-D NMR Spectroscopy; Academic Press: San Diego, 2012.
Return to citation in text: [1] -
Claramunt, R. M.; López, C.; García, M. Á.; Otero, M. D.; Torres, M. R.; Pinilla, E.; Alarcón, S. H.; Alkorta, I.; Elguero, J. New J. Chem. 2001, 25, 1061–1068. doi:10.1039/B103405G
Return to citation in text: [1] [2] -
Sanz, D.; Claramunt, R. M.; Saini, A.; Kumar, V.; Aggarwal, R.; Singh, S. P.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2007, 45, 513–517. doi:10.1002/mrc.1992
Return to citation in text: [1] [2] [3] -
Silva, A. M. S.; Sousa, R. M. S.; Jimeno, M. L.; Blanco, F.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2008, 46, 859–864. doi:10.1002/mrc.2272
Return to citation in text: [1] -
Seixas, R. S. G. R.; Silva, A. M. S.; Alkorta, I.; Elguero, J. Monatsh. Chem. 2011, 142, 731–742. doi:10.1007/s00706-011-0473-y
Return to citation in text: [1] -
Radula-Janik, K.; Kupka, T.; Ejsmont, K.; Daszkiewicz, Z.; Sauer, S. P. A. Magn. Reson. Chem. 2013, 51, 630–635. doi:10.1002/mrc.3992
Return to citation in text: [1] [2] -
Begtrup, M.; Elguero, J.; Faure, R.; Camps, P.; Estopá, C.; Ilavský, D.; Fruchier, A.; Marzin, C.; de Mendoza, J. Magn. Reson. Chem. 1988, 26, 134–151. doi:10.1002/mrc.1260260210
Return to citation in text: [1] -
Thakuria, H.; Das, G. ARKIVOC 2008, No. xv, 321–328.
Return to citation in text: [1] -
She, J.; Jiang, Z.; Wang, Y. Synlett 2009, 2023–2027. doi:10.1055/s-0029-1217515
Return to citation in text: [1] -
Zhang, D.; Yan, L. J. Phys. Chem. B 2010, 114, 12234–12241. doi:10.1021/jp1054606
Return to citation in text: [1] -
Alkorta, I.; Sánchez-Sanz, G.; Trujillo, C.; Elguero, J.; Claramunt, R. M. ARKIVOC 2012, No. ii, 85–106.
Return to citation in text: [1] -
Yu, B.; Zhang, H.; Zhao, Y.; Chen, S.; Xu, J.; Huang, C.; Liu, Z. Green Chem. 2013, 15, 95–99. doi:10.1039/C2GC36517K
Return to citation in text: [1] -
Claramunt, R. M.; Sanz, D.; Boyer, G.; Catalän, J.; de Paz, J. L. G.; Elguero, J. Magn. Reson. Chem. 1993, 31, 791–800. doi:10.1002/mrc.1260310902
Return to citation in text: [1] -
Claramunt, R. M.; Sanz, D.; López, C.; Jiménez, J. A.; Jimeno, M. L.; Elguero, J.; Fruchier, A. Magn. Reson. Chem. 1997, 35, 35–75. doi:10.1002/(SICI)1097-458X(199701)35:1<35::AID-OMR25>3.0.CO;2-K
Return to citation in text: [1] -
Claramunt, R. M.; López, C.; Sanz, D.; Alkorta, I.; Elguero, J. Heterocycles 2001, 55, 2109–2121. doi:10.3987/COM-01-9313
Return to citation in text: [1] -
Pinto, J.; Silva, V. L. M.; Silva, A. M. S.; Claramunt, R. M.; Sanz, D.; Torralba, M. C.; Torres, M. R.; Reviriego, F.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2013, 51, 203–221. doi:10.1002/mrc.3926
Return to citation in text: [1] -
Mercury - Crystal Structure Visualisation, Exploration and Analysis Made Easy. http://www.ccdc.cam.ac.uk/Solutions/CSDSystem/Pages/Mercury.aspx (accessed June 3, 2014).
Return to citation in text: [1] [2] -
Foces-Foces, C.; Trofimenko, S.; López, C.; Santa María, M. D.; Claramunt, R. M.; Elguero, J. J. Mol. Struct. 2000, 526, 59–64. doi:10.1016/S0022-2860(00)00444-0
Return to citation in text: [1] -
Sánchez-Migallón, A.; de la Hoz, A.; López, C.; Claramunt, R. M.; Infantes, L.; Motherwell, S.; Shankland, K.; Nowell, H.; Alkorta, I.; Elguero, J. Helv. Chim. Acta 2003, 86, 1026–1039. doi:10.1002/hlca.200390091
Return to citation in text: [1] -
Claramunt, R. M.; López, C.; Lott, S.; Santa María, M. D.; Alkorta, I.; Elguero, J. Helv. Chim. Acta 2005, 88, 1931–1942. doi:10.1002/hlca.200590148
Return to citation in text: [1] -
Virgili, A.; Quesada-Moreno, M. M.; Avilés-Moreno, J. R.; López-González, J. J.; García, M. A.; Claramunt, R. M.; Torres, M. R.; Jimeno, M. L.; Reviriego, F.; Alkorta, I.; Elguero, J. Helv. Chim. Acta 2014, 97, 471–490. doi:10.1002/hlca.201300395
Return to citation in text: [1] -
Webber, A. L.; Emsley, L.; Claramunt, R. M.; Brown, S. P. J. Phys. Chem. A 2010, 114, 10435–10442. doi:10.1021/jp104901j
Return to citation in text: [1] -
Sandström, J. Dynamic NMR Spectroscopy; Academic Press: London, 1982.
Return to citation in text: [1] -
Minkin, V. I.; Garnovskii, A. D.; Elguero, J.; Katritzky, A. R.; Denisko, O. V. Adv. Heterocycl. Chem. 2000, 76, 157–323. doi:10.1016/S0065-2725(00)76005-3
Return to citation in text: [1] [2] -
Elguero, J.; Llouquet, G.; Marzin, C. Tetrahedron Lett. 1975, 16, 4085–4086. doi:10.1016/S0040-4039(00)91243-7
Return to citation in text: [1] -
Claramunt, R. M.; López, C.; Alkorta, I.; Elguero, J.; Yang, R.; Schulman, S. Magn. Reson. Chem. 2004, 42, 712–714. doi:10.1002/mrc.1409
Return to citation in text: [1] -
Claramunt, R. M.; López, C.; Elguero, J. ARKIVOC 2006, No. v, 5–11.
Return to citation in text: [1] -
Ribeiro da Silva, M. A. V.; Ribeiro da Silva, M. D. M. C.; Amaral, L. M. P. F.; Elguero, J.; Jiménez, P.; Roux, M. V.; Dávalos, J. Z.; Temprado, M.; Cabildo, P.; Claramunt, R. M.; Mó, O.; Yáñez, M. J. Chem. Thermodyn. 2005, 37, 1168–1176. doi:10.1016/j.jct.2005.02.008
Return to citation in text: [1] -
Murphy, P. D. J. Magn. Reson. 1983, 52, 343–345.
Return to citation in text: [1] -
Murphy, P. D. J. Magn. Reson. 1985, 62, 303–308.
Return to citation in text: [1] -
Alemany, L. B.; Grant, D. M.; Alger, T. D.; Pugmire, R. J. J. Am. Chem. Soc. 1983, 105, 6697–6704. doi:10.1021/ja00360a025
Return to citation in text: [1] -
Gaussian 09, Revision A.1; Gaussian, Inc.: Wallingford, CT, 2009.
Return to citation in text: [1] -
London, F. J. Phys. Radium 1937, 8, 397–409. doi:10.1051/jphysrad:01937008010039700
Return to citation in text: [1] -
Ditchfield, R. Mol. Phys. 1974, 27, 789–807. doi:10.1080/00268977400100711
Return to citation in text: [1] -
Becke, A. D. Phys. Rev. A 1988, 38, 3098–3100. doi:10.1103/PhysRevA.38.3098
Return to citation in text: [1] -
Becke, A. D. J. Chem. Phys. 1993, 98, 5648–5652. doi:10.1063/1.464913
Return to citation in text: [1] -
Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785–789. doi:10.1103/PhysRevB.37.785
Return to citation in text: [1] -
Ditchfield, R.; Hehre, W. J.; Pople, J. A. J. Chem. Phys. 1971, 54, 724–728. doi:10.1063/1.1674902
Return to citation in text: [1] -
Frisch, M. J.; Pople, J. A.; Binkley, J. S. J. Chem. Phys. 1984, 80, 3265–3269. doi:10.1063/1.447079
Return to citation in text: [1] -
Mennucci, B.; Cammi, R., Eds. Continuum Solvation Models in Chemical Physics. From Theory to Applications; John Wiley & Sons: Chichester, 2007.
Return to citation in text: [1]
| 35. | Claramunt, R. M.; López, C.; Alkorta, I.; Elguero, J.; Yang, R.; Schulman, S. Magn. Reson. Chem. 2004, 42, 712–714. doi:10.1002/mrc.1409 |
| 36. | Claramunt, R. M.; López, C.; Elguero, J. ARKIVOC 2006, No. v, 5–11. |
| 33. | Minkin, V. I.; Garnovskii, A. D.; Elguero, J.; Katritzky, A. R.; Denisko, O. V. Adv. Heterocycl. Chem. 2000, 76, 157–323. doi:10.1016/S0065-2725(00)76005-3 |
| 37. | Ribeiro da Silva, M. A. V.; Ribeiro da Silva, M. D. M. C.; Amaral, L. M. P. F.; Elguero, J.; Jiménez, P.; Roux, M. V.; Dávalos, J. Z.; Temprado, M.; Cabildo, P.; Claramunt, R. M.; Mó, O.; Yáñez, M. J. Chem. Thermodyn. 2005, 37, 1168–1176. doi:10.1016/j.jct.2005.02.008 |
| 1. | Gomtsyan, A. Chem. Heterocycl. Compd. 2012, 48, 7–10. doi:10.1007/s10593-012-0960-z |
| 7. | Elguero, J.; Katritzky, A. R.; Denisko, O. V. Adv. Heterocycl. Chem. 2000, 76, 1–84. doi:10.1016/S0065-2725(00)76003-X |
| 8. | Alkorta, I.; Elguero, J. Top. Heterocycl. Chem. 2008, 19, 155–202. |
| 15. | Radula-Janik, K.; Kupka, T.; Ejsmont, K.; Daszkiewicz, Z.; Sauer, S. P. A. Magn. Reson. Chem. 2013, 51, 630–635. doi:10.1002/mrc.3992 |
| 5. | Pogorzelec-Glaser, K.; Rachocki, A.; Ławniczak, P.; Pietraszko, A.; Pawlaczyk, C.; Hilczer, B.; Pugaczowa-Michalska, M. CrystEngComm 2013, 15, 1950–1959. doi:10.1039/c2ce26571k |
| 6. | Rachocki, A.; Pogorzelec-Glaser, K.; Ławniczak, P.; Pugaczowa-Michalska, M.; Łapinski, A.; Hilczer, B.; Matczak, M.; Pietraszko, A. Cryst. Growth Des. 2014, 14, 1211–1220. doi:10.1021/cg401742b |
| 16. | Begtrup, M.; Elguero, J.; Faure, R.; Camps, P.; Estopá, C.; Ilavský, D.; Fruchier, A.; Marzin, C.; de Mendoza, J. Magn. Reson. Chem. 1988, 26, 134–151. doi:10.1002/mrc.1260260210 |
| 17. | Thakuria, H.; Das, G. ARKIVOC 2008, No. xv, 321–328. |
| 18. | She, J.; Jiang, Z.; Wang, Y. Synlett 2009, 2023–2027. doi:10.1055/s-0029-1217515 |
| 19. | Zhang, D.; Yan, L. J. Phys. Chem. B 2010, 114, 12234–12241. doi:10.1021/jp1054606 |
| 20. | Alkorta, I.; Sánchez-Sanz, G.; Trujillo, C.; Elguero, J.; Claramunt, R. M. ARKIVOC 2012, No. ii, 85–106. |
| 21. | Yu, B.; Zhang, H.; Zhao, Y.; Chen, S.; Xu, J.; Huang, C.; Liu, Z. Green Chem. 2013, 15, 95–99. doi:10.1039/C2GC36517K |
| 4. | Horiuchi, S.; Kagawa, F.; Hatahara, K.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Nat. Commun. 2012, 3, No. 1308. doi:10.1038/ncomms2322 |
| 12. | Sanz, D.; Claramunt, R. M.; Saini, A.; Kumar, V.; Aggarwal, R.; Singh, S. P.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2007, 45, 513–517. doi:10.1002/mrc.1992 |
| 47. | Ditchfield, R.; Hehre, W. J.; Pople, J. A. J. Chem. Phys. 1971, 54, 724–728. doi:10.1063/1.1674902 |
| 48. | Frisch, M. J.; Pople, J. A.; Binkley, J. S. J. Chem. Phys. 1984, 80, 3265–3269. doi:10.1063/1.447079 |
| 2. | Velík, J.; Baliharová, V.; Fink-Gremmels, J.; Bull, S.; Lamka, J.; Skálová, L. Res. Vet. Sci. 2004, 76, 95–108. doi:10.1016/j.rvsc.2003.08.005 |
| 3. | Khokra, S. L.; Choudhary, D. Asian J. Biochem. Pharm. Res. 2011, 1, 476–486. |
| 11. | Claramunt, R. M.; López, C.; García, M. Á.; Otero, M. D.; Torres, M. R.; Pinilla, E.; Alarcón, S. H.; Alkorta, I.; Elguero, J. New J. Chem. 2001, 25, 1061–1068. doi:10.1039/B103405G |
| 14. | Seixas, R. S. G. R.; Silva, A. M. S.; Alkorta, I.; Elguero, J. Monatsh. Chem. 2011, 142, 731–742. doi:10.1007/s00706-011-0473-y |
| 49. | Mennucci, B.; Cammi, R., Eds. Continuum Solvation Models in Chemical Physics. From Theory to Applications; John Wiley & Sons: Chichester, 2007. |
| 11. | Claramunt, R. M.; López, C.; García, M. Á.; Otero, M. D.; Torres, M. R.; Pinilla, E.; Alarcón, S. H.; Alkorta, I.; Elguero, J. New J. Chem. 2001, 25, 1061–1068. doi:10.1039/B103405G |
| 13. | Silva, A. M. S.; Sousa, R. M. S.; Jimeno, M. L.; Blanco, F.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2008, 46, 859–864. doi:10.1002/mrc.2272 |
| 42. | London, F. J. Phys. Radium 1937, 8, 397–409. doi:10.1051/jphysrad:01937008010039700 |
| 43. | Ditchfield, R. Mol. Phys. 1974, 27, 789–807. doi:10.1080/00268977400100711 |
| 12. | Sanz, D.; Claramunt, R. M.; Saini, A.; Kumar, V.; Aggarwal, R.; Singh, S. P.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2007, 45, 513–517. doi:10.1002/mrc.1992 |
| 44. | Becke, A. D. Phys. Rev. A 1988, 38, 3098–3100. doi:10.1103/PhysRevA.38.3098 |
| 45. | Becke, A. D. J. Chem. Phys. 1993, 98, 5648–5652. doi:10.1063/1.464913 |
| 46. | Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785–789. doi:10.1103/PhysRevB.37.785 |
| 4. | Horiuchi, S.; Kagawa, F.; Hatahara, K.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Nat. Commun. 2012, 3, No. 1308. doi:10.1038/ncomms2322 |
| 38. | Murphy, P. D. J. Magn. Reson. 1983, 52, 343–345. |
| 39. | Murphy, P. D. J. Magn. Reson. 1985, 62, 303–308. |
| 40. | Alemany, L. B.; Grant, D. M.; Alger, T. D.; Pugmire, R. J. J. Am. Chem. Soc. 1983, 105, 6697–6704. doi:10.1021/ja00360a025 |
| 9. | Weber, U.; Thiele, H. NMR Spectroscopy: Modern Spectral Analysis,; Wiley-VCH: Weinheim, 1998. |
| 10. | Simpson, J. H. Organic Structure Determination using 2-D NMR Spectroscopy; Academic Press: San Diego, 2012. |
| 12. | Sanz, D.; Claramunt, R. M.; Saini, A.; Kumar, V.; Aggarwal, R.; Singh, S. P.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2007, 45, 513–517. doi:10.1002/mrc.1992 |
| 25. | Pinto, J.; Silva, V. L. M.; Silva, A. M. S.; Claramunt, R. M.; Sanz, D.; Torralba, M. C.; Torres, M. R.; Reviriego, F.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2013, 51, 203–221. doi:10.1002/mrc.3926 |
| 22. | Claramunt, R. M.; Sanz, D.; Boyer, G.; Catalän, J.; de Paz, J. L. G.; Elguero, J. Magn. Reson. Chem. 1993, 31, 791–800. doi:10.1002/mrc.1260310902 |
| 23. | Claramunt, R. M.; Sanz, D.; López, C.; Jiménez, J. A.; Jimeno, M. L.; Elguero, J.; Fruchier, A. Magn. Reson. Chem. 1997, 35, 35–75. doi:10.1002/(SICI)1097-458X(199701)35:1<35::AID-OMR25>3.0.CO;2-K |
| 24. | Claramunt, R. M.; López, C.; Sanz, D.; Alkorta, I.; Elguero, J. Heterocycles 2001, 55, 2109–2121. doi:10.3987/COM-01-9313 |
| 33. | Minkin, V. I.; Garnovskii, A. D.; Elguero, J.; Katritzky, A. R.; Denisko, O. V. Adv. Heterocycl. Chem. 2000, 76, 157–323. doi:10.1016/S0065-2725(00)76005-3 |
| 34. | Elguero, J.; Llouquet, G.; Marzin, C. Tetrahedron Lett. 1975, 16, 4085–4086. doi:10.1016/S0040-4039(00)91243-7 |
| 31. | Webber, A. L.; Emsley, L.; Claramunt, R. M.; Brown, S. P. J. Phys. Chem. A 2010, 114, 10435–10442. doi:10.1021/jp104901j |
| 26. | Mercury - Crystal Structure Visualisation, Exploration and Analysis Made Easy. http://www.ccdc.cam.ac.uk/Solutions/CSDSystem/Pages/Mercury.aspx (accessed June 3, 2014). |
| 15. | Radula-Janik, K.; Kupka, T.; Ejsmont, K.; Daszkiewicz, Z.; Sauer, S. P. A. Magn. Reson. Chem. 2013, 51, 630–635. doi:10.1002/mrc.3992 |
| 4. | Horiuchi, S.; Kagawa, F.; Hatahara, K.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Nat. Commun. 2012, 3, No. 1308. doi:10.1038/ncomms2322 |
| 26. | Mercury - Crystal Structure Visualisation, Exploration and Analysis Made Easy. http://www.ccdc.cam.ac.uk/Solutions/CSDSystem/Pages/Mercury.aspx (accessed June 3, 2014). |
| 27. | Foces-Foces, C.; Trofimenko, S.; López, C.; Santa María, M. D.; Claramunt, R. M.; Elguero, J. J. Mol. Struct. 2000, 526, 59–64. doi:10.1016/S0022-2860(00)00444-0 |
| 28. | Sánchez-Migallón, A.; de la Hoz, A.; López, C.; Claramunt, R. M.; Infantes, L.; Motherwell, S.; Shankland, K.; Nowell, H.; Alkorta, I.; Elguero, J. Helv. Chim. Acta 2003, 86, 1026–1039. doi:10.1002/hlca.200390091 |
| 29. | Claramunt, R. M.; López, C.; Lott, S.; Santa María, M. D.; Alkorta, I.; Elguero, J. Helv. Chim. Acta 2005, 88, 1931–1942. doi:10.1002/hlca.200590148 |
| 30. | Virgili, A.; Quesada-Moreno, M. M.; Avilés-Moreno, J. R.; López-González, J. J.; García, M. A.; Claramunt, R. M.; Torres, M. R.; Jimeno, M. L.; Reviriego, F.; Alkorta, I.; Elguero, J. Helv. Chim. Acta 2014, 97, 471–490. doi:10.1002/hlca.201300395 |
© 2014 Nieto et al; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)