Abstract
Chiral acrylic esters derived from biomass were developed as models to have a better insight in the aryl–vinyl π-stacking interactions. Quantum chemical calculations, NMR studies and experimental evidences demonstrated the presence of equilibriums of at least four different conformations: π-stacked and face-to-edge, each of them in an s-cis/s-trans conformation. The results show that the stabilization produced by the π–π interaction makes the π-stacked conformation predominant in solution and this stabilization is slightly affected by the electron density of the aromatic counterpart.
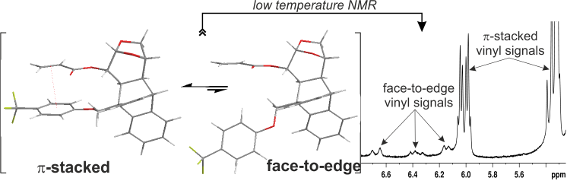
Graphical Abstract
Introduction
Noncovalent interactions have demonstrated to have relevant importance in chemistry and biology [1-4]. Considering all noncovalent interactions, π-stacking is perhaps the less well understood, although its application in materials sciences, enzyme design and template-directed synthesis have had a dramatic growth, mainly for arene–arene interactions [1-8]. In particular, the use of π–π overlap as an element of stereocontrol in highly selective chemical transformations has been widely explored [9]. In this context, as part of our continuous interest in the development of new tools for asymmetric synthesis using levoglucosenone (a biomass-derived chiral enone) [10-15], we reported the synthesis of a novel chiral auxiliary that demonstrated to be very efficient in an asymmetric Diels–Alder reaction between the acrylic ester derivative and cyclopentadiene [16]. The facial selectivity of this reaction proved to be due to an aryl–vinyl π-stacking intramolecular interaction that fixed the conformation of the dienophile (Figure 1) [16].
Figure 1: Intramolecular aryl–vinyl π-stacking interaction of a levoglucosenone derivative.
Figure 1: Intramolecular aryl–vinyl π-stacking interaction of a levoglucosenone derivative.
Given this precedent, we aimed to gain further insight into this type of interaction, by exploring the effect caused by the introduction of electronically different substituents at the aromatic ring of the chiral auxiliary. For this reason, we planned to synthesize the acrylic esters, structurally related to the previously reported acrylate, with CF3 and OMe groups in the para position of the phenoxy group as representative electron-withdrawing and releasing groups, respectively. The π–π interaction was studied by combining experimental, spectroscopic and computational evidence of the structurally related chiral acrylates to get new insights into the alkene–arene intramolecular interaction. Besides, it was evaluated the effect of the electron density of the aromatic counterpart and its influence on the asymmetric inductive capacity of the auxiliary.
Results and Discussion
The synthesis of acrylate derivatives 6a,b bearing CF3 and OMe substituents in the para position of the phenoxy group is depicted in Scheme 1. Levoglucosenone (1) was used as a dienophile to react with the corresponding 9-substituted anthracenes 2a,b, which are easily prepared from commercially available 9-anthracenyl methanol. When the Diels–Alder reactions were carried out in refluxing toluene, the desired ortho adducts 3a and 3b were obtained in good yields of 71% and 86%, respectively. However, the long reaction times (8–9 days) prompted us to evaluate these chemical transformations under microwave irradiation [17], affording the cycloadducts 3a,b in very good yields (76–81%) after irradiating a THF solution of 1 and 2 at 150 °C during 4 hours. The reduction of the ketone group in 3 with NaBH4 produced alcohols 4 and 5 in excellent yields and a ratio of about 40:60. The diastereomeric mixture of 4 and 5 was easily separated by flash chromatography. Finally, acrylates 6a,b were prepared by reaction of the corresponding alcohol 5 with acryloyl chloride in the presence of Et3N at 0 °C. The corresponding acrylic ester could not be obtained from the epimeric alcohols 4, probably because of the steric hindrance surrounding the alcohol position. Therefore, alcohols 4 were recycled by oxidation with PCC regenerating 3 in very good yields, and increasing the overall yield of acrylates 6.
The 1H NMR spectra of compounds 6a and 6b (300 MHz, CDCl3) showed an important shielding effect of the vinylic protons at 6.10–5.38 and 6.18–5.47 ppm, respectively (Figure 2), compared to those of analogous acrylates without an aromatic substituent at the benzylic position (6.57–5.87 ppm) [12,13]. The magnitude of this shielding, slightly more pronounced for 6a, was in the range of a previous reported acrylate with a pendant phenoxy group 6c (6.14–5.41 ppm) [16]. This effect is interpreted in terms of the anisotropy phenomena caused by the proximity of the aromatic ring to the double bond. Another salient observation is the broadening of the vinylic signals that can be associated to a dynamic process taking place at room temperature.
Figure 2: Vinyl region of the 1H NMR spectra of 6a–d in CDCl3 at 300 K.
Figure 2: Vinyl region of the 1H NMR spectra of 6a–d in CDCl3 at 300 K.
In order to unravel the origin of this phenomenon, we further carried out low temperature NMR studies (Figure 3). When the CDCl3 solution of acrylate 6a was cooled gradually from 300 K the resonances corresponding to the vinylic protons broaden (283 and 273 K) and at 233 K two different shielding zones were detected for these protons at 6.70–6.13 and 6.06–5.30 ppm (Figure 3 and for further details, see Supporting Information File 1). This phenomenon could be interpreted in terms of the existence of 2 species present in solution in approximately a 9:1 ratio, according to the relative area of the signals. Some authors have claimed that this effect could be due to a conformational equilibrium of s-cis and s-trans species that is shifted toward the s-trans conformer at lower temperatures [18-21].
Figure 3: Vinylic region of the low temperatures 1H NMR spectra of 6a in CDCl3.
Figure 3: Vinylic region of the low temperatures 1H NMR spectra of 6a in CDCl3.
Similar studies were carried out for acrylates 6b and 6c demonstrating analogous behaviors. Although the low temperature NMR studies for acrylate 6c were already reported, it was not perceived the presence of the second set of vinylic signals between 6.70 and 6.10 ppm at 233 K [16].
In order to have a better understanding of this conformational dynamics, we further carried out a detailed computational study at the M06-2X level of theory [22] for the three acrylates 6a–c. This meta-GGA functional, developed by Truhlar [23] has been shown to be one of the approaches of choice to model noncovalent interactions [9]. After a complete exploration of the potential energy surface (PES) at the M06-2X/6-31+G(d) level of theory, four local minima were located for each system, namely: gauche_s-cis, gauche_s-trans, anti_s-cis and anti_s-trans (Figure 4) [24]. In the gauche rotamers (the most stable found in each system), the phenoxy and acrylate moieties lie parallel to each other, and the distances from the centroid of the aromatic ring to the midpoint of the C=C double bond are in the range of 3.25–3.31 Å, consistent with the distances for other π-stacked systems [2]. On the other hand, in the anti conformers the remoteness of the phenyl and alkene groups prevents any stabilizing interaction between them. For the gauche conformations, NBO analysis [25,26] (at the M06-2X/6-31+G(d) level) revealed a two-electron stabilizing donation from the π orbital of the phenoxy ring to the π* anti-bonding orbital of the acrylate moiety, supporting the through-space interaction between these fragments. The associated second order perturbation energies (ΔE(2)) are in the range of −0.90 to −0.73 kcal/mol for 6-gauche_s-cis and −0.84 to −0.69 kcal/mol for 6-gauche_s-trans. The energy (ZPE) difference between gauche and anti conformations (ΔEag = Eanti − Egauche) can be seen as a measurement of the stabilization caused by the intramolecular interaction. The ΔEag values computed for all acrylate derivatives 6 show that ΔEag for acrylate 6a is higher than that for 6b and 6c (3.91 kcal/mol vs 3.49 kcal/mol vs 3.27 kcal/mol, respectively), suggesting a slightly stronger interaction for 6a (see Supporting Information File 1 for further details).
Figure 4: M06-2X/6-31+G(d) Gibbs free energy profiles (in kcal/mol) computed for the conformational equilibriums of 6a–c.
Figure 4: M06-2X/6-31+G(d) Gibbs free energy profiles (in kcal/mol) computed for the conformational equilibri...
To shed light on these issues, we next computed the interaction energies for the complexes of methyl acrylate (7) and 4-trifluoromethylanisole (8), 4-methoxyanisole (9) or anisole (10), (Scheme 2).
Scheme 2: Complexes between methyl acrylate (7) and representative anisole derivatives.
Scheme 2: Complexes between methyl acrylate (7) and representative anisole derivatives.
For the complexes in s-cis conformation, the π–π interaction energy computed at the M06-2X/6-31+G(d) level is −7.2 kcal/mol for 7 + 8, −6.9 kcal/mol for 7 + 9 and −6.5 kcal/mol for 7 + 10 (similar values were computed for 7 in its s-trans conformation, see Supporting Information File 1). Similar trends were found at the MP2/6-31+G(d) level of theory. NBO calculations indicated that in these π-stacked complexes, the charge transfer (CT) takes place from the aromatic compound to the acrylate. Despite the amount of CT is higher for the more electron-rich ring 9 (0.013e vs 0.011e (8) vs 0.008e (10)), according to the results presented herein, the extra stabilization of the CF3 substituted systems cannot be due to polar or charge-transfer effects but rather from dispersion interactions [27]. In an effort to prove this hypothesis, we performed an energy decomposition analysis (EDA) at the B3LYP-D3/TZ2P level using ADF. In this approach, the interaction energy (ΔEi) is decomposed as the sum of four terms [28]: ΔEi = ΔVelstat + ΔEPauli + ΔEoi + ΔEdisp, where ΔVelstat accounts for the usually attractive classical electrostatic interaction between the deformed fragments, ΔEPauli, the Pauli repulsion term, represents the destabilizing interactions between the occupied orbitals (steric repulsion), ΔEoi shows the interaction between orbitals (including all electron-pair bondings, HOMO–LUMO charge-transfer processes, polarization interactions, etc.), and ΔEdisp refers to the effect exerted by dispersion forces. As shown in Table 1 a slightly higher interaction energy was found for 7 + 8 (−7.7 kcal/mol). It is important to point out the great significance of the dispersion forces in these π-stacked complexes, representing ≈60% of the total attractive forces.
Table 1: Energy decomposition analysis (EDA) of the three complexes shown in Scheme 2.
| 7 + 8 | 7 + 9 | 7 + 10 | |
|---|---|---|---|
| ΔEi | −7.7 | −7.2 | −6.8 |
| ΔEPauli | 17.9 | 18.2 | 17.7 |
| ΔVelstat | −9.8 (38%) | −9.5 (37%) | −9.3 (36%) |
| ΔEoi | −3.8 (16%) | −4.1 (17%) | −3.9 (17%) |
| ΔEdisp | −12.0 (61%) | −11.8 (60%) | −11.3 (57%) |
Noteworthy, the distances from the centroid of the aromatic ring to the midpoint of the double bond, calculated at both levels of theory for the complexes of 7 and anisole derivatives 8–10 are between 3.23–3.29 Å which is in excellent agreement with the distances calculated for the π-stacked conformations of 6a–c shown in Figure 4.
As depicted in Figure 4, the energy barriers computed for the s-cis/s-trans conversion of 6a–c are low (6.3–7.5 kcal/mol), suggesting a fast equilibration even at low temperatures. On the other hand, the barriers calculated for the anti/gauche interconversion are considerably higher (14.7–16.2 kcal/mol). This slow conformational change can be responsible not only for the broadening of the NMR signals of some nuclei at room temperature, but also for the NMR splitting observed upon cooling. In the gauche conformers a significant shielding of the vinyl protons is expected, while in the anti rotamers those nuclei should not be affected by the ring current exerted by the aromatic substituent. In addition, the relative intensity of these two sets of NMR signals should be related to the Boltzmann distribution of both types of conformations. Accordingly, the gauche/anti ratios computed from the Gibbs free energies are 97:3 (6a), 95:5 (6b) and 91:9 (6c) in very good agreement with the average 9:1 value experimentally obtained from the low temperature NMR spectra. Moreover, the higher population of the π-stacked conformers found for 6a accounts for the magnitude of the shielding of the acrylate protons (Figure 2). In an additional effort to understand the extent to which the π–π interactions affect the conformational equilibriums of a system, we next explored the M06-2X/6-31+G(d) PES of acrylate 6d bearing a methoxymethyl group at the benzylic position of the molecule (Figure 5). With the lack of stabilizing π-stacking, both gauche and anti conformations are of similar energy. In fact, the anti_s-cis rotamer is the global minima. Moreover, while the s-cis/s-trans conversion is still predicted to be very fast, the barriers computed for the gauche/anti equilibration are lower (≈13 kcal/mol), reinforcing the fact that the π-stacking interaction also affects the equilibrium kinetics.
Figure 5: Comparison of the M06-2X/6-31+G(d) energy profiles (in kcal/mol) computed for 6d and 6b (in grey).
Figure 5: Comparison of the M06-2X/6-31+G(d) energy profiles (in kcal/mol) computed for 6d and 6b (in grey).
In order to better understand the conformational studies, a crystal of acrylate 6a suitable for X-ray diffraction analysis was obtained (for further information, see Supporting Information File 1). The crystal structure shows the vinyl and aromatic groups in a face-to-edge arrangement, with a dihedral angle of 73.8(2)° between the groups’ mean planes (Figure 6 and Supporting Information File 1). The distance between the centroid of the arene and the middle point of the C=C double bond is 6.48 Å. The conformation found in the solid state is in full agreement with the calculated structure 6a-anti_s-trans (Figure 4). This face-to-edge conformation accounts for the resonance signals of the vinylic hydrogens of the minor species detected at 233 K in the 1H NMR spectrum. It is assumed that the minor species was the one found in the crystal structure due to crystal lattice stabilization.
![[1860-5397-12-158-6]](/bjoc/content/figures/1860-5397-12-158-6.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: X-ray thermal ellipsoid plot of 6a (50% probability level) showing the labeling scheme (hydrogen and carbon labels have been omitted for clarity).
Figure 6: X-ray thermal ellipsoid plot of 6a (50% probability level) showing the labeling scheme (hydrogen an...
These experimental and theoretical results led us to postulate that acrylates 6a–c are present in a conformational equilibrium between at least 4 different species: π-stacked and face-to-edge, and each of them in an s-cis/s-trans conformation. This equilibrium is affected by the strength of the π–π interaction, which is slightly higher for the electron-withdrawing substituted phenoxy ring. The lower amount of the minor face-to-edge species detected in the low temperature 1H NMR spectrum of 6a, along with the more shielded protons of the vinyl group at room temperature, account for this explanation.
With the aim to determine if the strength of the intramolecular π-stacking interaction can have any influence in the inductive capacity, we studied the Diels–Alder reaction of acrylates 6a,b with cyclopentadiene (Table 2).
Table 2: Thermal and Lewis acid promoted Diels–Alder reactions of 6a,b and cyclopentadiene.
|
|
|||||||
| Entry | Acrylate | Lewis acid | T (°C) | t (h) | Yield (%)a | endo/exob | endo R/Sb |
|---|---|---|---|---|---|---|---|
| 1 | 6a | – | 25 | 144 | 92 | 80:20 | 12:88 |
| 2 | 6a | Et2AlCl | 0 | 1 | 75 | 92:8 | 92:8 |
| 3 | 6b | – | 25 | 96 | 92 | 78:22 | 18:82 |
| 4 | 6b | Et2AlCl | 0 | 1 | 80 | 92:8 | 94:6 |
aYield corresponds to isolated products. bDetermined by HPLC.
All cycloadditions were endo diastereoselective as predicted by the Alder´s rule. The reaction between 6a or 6b and cyclopentadiene carried out at room temperature showed a high stereoselectivity (Table 2, entries 1 and 3, respectively). These results are similar to the ones previously reported for 6c (endo R/S 13:87) [16]. Noticeably, the endo S/R ratios are considerable high in the absence of Lewis acids. The high inductive capacity is interpreted in terms of the fact that the conformation of the dienophile is fixed by a π-stacking interaction. The reactions promoted by Et2AlCl produced the reversed endo S/R diastereoselectivity with a concomitant increase in the endo/exo ratio, as found for other related systems [11,13,16]. These results were interpreted in terms of the formation of an aluminum-chelated species with the acryloyl oxygen and the oxygen of the 1,6-anhydro bridge, according to the NMR studies (see Supporting Information File 1). Saponification of adducts 11 and 12 provided the free 5-norbornenecarboxylic acid and the chiral auxiliaries 5a and 5b in excellent yields, which can be reused.
Conclusion
We have reported the synthesis of chiral acrylates derived from renewable feedstock as models to study arene–alkene π-stacking interactions. To the best of our knowledge this is the first report that provides experimental and computational evidences to understand the effect of such intramolecular interactions in the conformational dynamics of the system. This equilibrium, that involves a fast s-cis/s-trans exchange and a slow π-stacked/face-to-edge conversion, depends on the strength of the π–π interaction, which is slightly higher when the arene moiety is substituted with an electron-withdrawing group. The results presented herein will allow for better understanding the intramolecular interactions between alkenes and aromatic rings. This can be useful in several fields, such as supramolecular chemistry, biology and material science and, in particular, in the area of asymmetric synthesis for the rational design of new elements of stereocontrol.
Supporting Information
| Supporting Information File 1: Experimental procedures, characterization and spectral data for synthesized compounds and X-ray data for compound 6a. | ||
| Format: PDF | Size: 3.9 MB | Download |
Acknowledgements
This research was supported by grants from Universidad Nacional de Rosario, Consejo Nacional de Investigaciones Científicas y Técnicas and Agencia Nacional de Promoción Científica y Tecnológica, Argentina. VC thanks CONICET and Fundación Josefina Prats for the award of a fellowship. We thank Prof. Miguel Angel Sierra for helpful discussions.
References
-
Salonen, L. M.; Ellermann, M.; Diederich, F. Angew. Chem., Int. Ed. 2011, 50, 4808–4842. doi:10.1002/anie.201007560
Return to citation in text: [1] [2] -
Jones, G. B. Tetrahedron 2001, 57, 7999–8016. doi:10.1016/S0040-4020(01)00753-0
Return to citation in text: [1] [2] [3] -
Müller-Dethlefs, K.; Hobza, P. Chem. Rev. 2000, 100, 143–168. doi:10.1021/cr9900331
Return to citation in text: [1] [2] -
Kim, K. S.; Tarakeshwar, P.; Lee, J. Y. Chem. Rev. 2000, 100, 4145–4186. doi:10.1021/cr990051i
Return to citation in text: [1] [2] -
Wheeler, S. E.; McNeil, A. J.; Müller, P.; Swager, T. M.; Houk, K. N. J. Am. Chem. Soc. 2010, 132, 3304–3311. doi:10.1021/ja903653j
Return to citation in text: [1] -
Wheeler, S. E.; Houk, K. N. J. Am. Chem. Soc. 2008, 130, 10854–10855. doi:10.1021/ja802849j
Return to citation in text: [1] -
Hwang, J.; Dial, B. E.; Li, P.; Kozik, M. E.; Smith, M. D.; Shimizu, K. D. Chem. Sci. 2015, 6, 4358–4364. doi:10.1039/C5SC01370D
Return to citation in text: [1] -
Hwang, J.; Li, P.; Carroll, W. R.; Smith, M. D.; Pellechia, P. J.; Shimizu, K. D. J. Am. Chem. Soc. 2014, 136, 14060–14067. doi:10.1021/ja504378p
Return to citation in text: [1] -
Krenske, E. H.; Houk, K. N. Acc. Chem. Res. 2013, 46, 979–989. doi:10.1021/ar3000794
Return to citation in text: [1] [2] -
Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G.; Echeverría, G. A.; Piro, O. E. Org. Lett. 2012, 14, 2556–2559. doi:10.1021/ol3008588
Return to citation in text: [1] -
Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G. Tetrahedron 2009, 65, 3502–3508. doi:10.1016/j.tet.2009.02.020
Return to citation in text: [1] [2] -
Sarotti, A. M.; Spanevello, R. A.; Duhayon, C.; Tuchagues, J.-P.; Suárez, A. G. Tetrahedron 2007, 63, 241–251. doi:10.1016/j.tet.2006.10.028
Return to citation in text: [1] [2] -
Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G. Org. Lett. 2006, 8, 1487–1490. doi:10.1021/ol0603099
Return to citation in text: [1] [2] [3] -
Sarotti, A. M.; Zanardi, M. M.; Spanevello, R. A.; Suárez, A. G. Curr. Org. Synth. 2012, 9, 439–459. doi:10.2174/157017912802651401
Return to citation in text: [1] -
Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G. Green Chem. 2007, 9, 1137–1140. doi:10.1039/b703690f
Return to citation in text: [1] -
Sarotti, A. M.; Fernández, I.; Spanevello, R. A.; Sierra, M. Á.; Suárez, A. G. Org. Lett. 2008, 10, 3389–3392. doi:10.1021/ol801140g
Return to citation in text: [1] [2] [3] [4] [5] [6] -
Sarotti, A. M.; Joullié, M. M.; Spanevello, R. A.; Suárez, A. G. Org. Lett. 2006, 8, 5561–5564. doi:10.1021/ol062254g
Return to citation in text: [1] -
Dumas, F.; Mezrhab, B.; d'Angelo, J. J. Org. Chem. 1996, 61, 2293–2304. doi:10.1021/jo951414r
Return to citation in text: [1] -
Gung, B. W.; Yanik, M. M. J. Org. Chem. 1996, 61, 947–951. doi:10.1021/jo951625w
Return to citation in text: [1] -
Mezrhab, B.; Dumas, F.; d'Angelo, J.; Riche, C. J. Org. Chem. 1994, 59, 500–503. doi:10.1021/jo00081a039
Return to citation in text: [1] -
Dussault, P. H.; Woller, K. R.; Hillier, M. C. Tetrahedron 1994, 50, 8929–8940. doi:10.1016/S0040-4020(01)85363-1
Return to citation in text: [1] -
Gaussian 09, Revision B.01; Gaussian, Inc.: Wallingford, CT, 2009.
Return to citation in text: [1] -
Zhao, Y.; Truhlar, D. G. Acc. Chem. Res. 2008, 41, 157–167. doi:10.1021/ar700111a
Return to citation in text: [1] -
In the gauche and anti conformations the C3–C3a–C7–O dihedral angles are ≈60° and ≈180°, respectively.
Return to citation in text: [1] -
Reed, A. E.; Weinstock, R. B.; Weinhold, F. J. Chem. Phys. 1985, 83, 735–746. doi:10.1063/1.449486
Return to citation in text: [1] -
Reed, A. E.; Curtiss, L. A.; Weinhold, F. Chem. Rev. 1988, 88, 899–926. doi:10.1021/cr00088a005
Return to citation in text: [1] -
Harris, L. D.; Platts, J. A.; Tomkinson, N. C. O. Org. Biomol. Chem. 2003, 1, 457–459. doi:10.1039/b210497k
Return to citation in text: [1] -
Bickelhaupt, F. M.; Baerends, E. J. In Reviews in Computational Chemistry; Lipkowitz, K. B.; Boyd, D. B., Eds.; Wiley-VCH: New York, 2000; Vol. 15, pp 1–86. doi:10.1002/9780470125922.ch1
Return to citation in text: [1]
| 28. | Bickelhaupt, F. M.; Baerends, E. J. In Reviews in Computational Chemistry; Lipkowitz, K. B.; Boyd, D. B., Eds.; Wiley-VCH: New York, 2000; Vol. 15, pp 1–86. doi:10.1002/9780470125922.ch1 |
| 25. | Reed, A. E.; Weinstock, R. B.; Weinhold, F. J. Chem. Phys. 1985, 83, 735–746. doi:10.1063/1.449486 |
| 26. | Reed, A. E.; Curtiss, L. A.; Weinhold, F. Chem. Rev. 1988, 88, 899–926. doi:10.1021/cr00088a005 |
| 27. | Harris, L. D.; Platts, J. A.; Tomkinson, N. C. O. Org. Biomol. Chem. 2003, 1, 457–459. doi:10.1039/b210497k |
| 1. | Salonen, L. M.; Ellermann, M.; Diederich, F. Angew. Chem., Int. Ed. 2011, 50, 4808–4842. doi:10.1002/anie.201007560 |
| 2. | Jones, G. B. Tetrahedron 2001, 57, 7999–8016. doi:10.1016/S0040-4020(01)00753-0 |
| 3. | Müller-Dethlefs, K.; Hobza, P. Chem. Rev. 2000, 100, 143–168. doi:10.1021/cr9900331 |
| 4. | Kim, K. S.; Tarakeshwar, P.; Lee, J. Y. Chem. Rev. 2000, 100, 4145–4186. doi:10.1021/cr990051i |
| 16. | Sarotti, A. M.; Fernández, I.; Spanevello, R. A.; Sierra, M. Á.; Suárez, A. G. Org. Lett. 2008, 10, 3389–3392. doi:10.1021/ol801140g |
| 24. | In the gauche and anti conformations the C3–C3a–C7–O dihedral angles are ≈60° and ≈180°, respectively. |
| 10. | Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G.; Echeverría, G. A.; Piro, O. E. Org. Lett. 2012, 14, 2556–2559. doi:10.1021/ol3008588 |
| 11. | Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G. Tetrahedron 2009, 65, 3502–3508. doi:10.1016/j.tet.2009.02.020 |
| 12. | Sarotti, A. M.; Spanevello, R. A.; Duhayon, C.; Tuchagues, J.-P.; Suárez, A. G. Tetrahedron 2007, 63, 241–251. doi:10.1016/j.tet.2006.10.028 |
| 13. | Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G. Org. Lett. 2006, 8, 1487–1490. doi:10.1021/ol0603099 |
| 14. | Sarotti, A. M.; Zanardi, M. M.; Spanevello, R. A.; Suárez, A. G. Curr. Org. Synth. 2012, 9, 439–459. doi:10.2174/157017912802651401 |
| 15. | Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G. Green Chem. 2007, 9, 1137–1140. doi:10.1039/b703690f |
| 2. | Jones, G. B. Tetrahedron 2001, 57, 7999–8016. doi:10.1016/S0040-4020(01)00753-0 |
| 9. | Krenske, E. H.; Houk, K. N. Acc. Chem. Res. 2013, 46, 979–989. doi:10.1021/ar3000794 |
| 23. | Zhao, Y.; Truhlar, D. G. Acc. Chem. Res. 2008, 41, 157–167. doi:10.1021/ar700111a |
| 1. | Salonen, L. M.; Ellermann, M.; Diederich, F. Angew. Chem., Int. Ed. 2011, 50, 4808–4842. doi:10.1002/anie.201007560 |
| 2. | Jones, G. B. Tetrahedron 2001, 57, 7999–8016. doi:10.1016/S0040-4020(01)00753-0 |
| 3. | Müller-Dethlefs, K.; Hobza, P. Chem. Rev. 2000, 100, 143–168. doi:10.1021/cr9900331 |
| 4. | Kim, K. S.; Tarakeshwar, P.; Lee, J. Y. Chem. Rev. 2000, 100, 4145–4186. doi:10.1021/cr990051i |
| 5. | Wheeler, S. E.; McNeil, A. J.; Müller, P.; Swager, T. M.; Houk, K. N. J. Am. Chem. Soc. 2010, 132, 3304–3311. doi:10.1021/ja903653j |
| 6. | Wheeler, S. E.; Houk, K. N. J. Am. Chem. Soc. 2008, 130, 10854–10855. doi:10.1021/ja802849j |
| 7. | Hwang, J.; Dial, B. E.; Li, P.; Kozik, M. E.; Smith, M. D.; Shimizu, K. D. Chem. Sci. 2015, 6, 4358–4364. doi:10.1039/C5SC01370D |
| 8. | Hwang, J.; Li, P.; Carroll, W. R.; Smith, M. D.; Pellechia, P. J.; Shimizu, K. D. J. Am. Chem. Soc. 2014, 136, 14060–14067. doi:10.1021/ja504378p |
| 9. | Krenske, E. H.; Houk, K. N. Acc. Chem. Res. 2013, 46, 979–989. doi:10.1021/ar3000794 |
| 16. | Sarotti, A. M.; Fernández, I.; Spanevello, R. A.; Sierra, M. Á.; Suárez, A. G. Org. Lett. 2008, 10, 3389–3392. doi:10.1021/ol801140g |
| 16. | Sarotti, A. M.; Fernández, I.; Spanevello, R. A.; Sierra, M. Á.; Suárez, A. G. Org. Lett. 2008, 10, 3389–3392. doi:10.1021/ol801140g |
| 12. | Sarotti, A. M.; Spanevello, R. A.; Duhayon, C.; Tuchagues, J.-P.; Suárez, A. G. Tetrahedron 2007, 63, 241–251. doi:10.1016/j.tet.2006.10.028 |
| 13. | Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G. Org. Lett. 2006, 8, 1487–1490. doi:10.1021/ol0603099 |
| 17. | Sarotti, A. M.; Joullié, M. M.; Spanevello, R. A.; Suárez, A. G. Org. Lett. 2006, 8, 5561–5564. doi:10.1021/ol062254g |
| 16. | Sarotti, A. M.; Fernández, I.; Spanevello, R. A.; Sierra, M. Á.; Suárez, A. G. Org. Lett. 2008, 10, 3389–3392. doi:10.1021/ol801140g |
| 16. | Sarotti, A. M.; Fernández, I.; Spanevello, R. A.; Sierra, M. Á.; Suárez, A. G. Org. Lett. 2008, 10, 3389–3392. doi:10.1021/ol801140g |
| 18. | Dumas, F.; Mezrhab, B.; d'Angelo, J. J. Org. Chem. 1996, 61, 2293–2304. doi:10.1021/jo951414r |
| 19. | Gung, B. W.; Yanik, M. M. J. Org. Chem. 1996, 61, 947–951. doi:10.1021/jo951625w |
| 20. | Mezrhab, B.; Dumas, F.; d'Angelo, J.; Riche, C. J. Org. Chem. 1994, 59, 500–503. doi:10.1021/jo00081a039 |
| 21. | Dussault, P. H.; Woller, K. R.; Hillier, M. C. Tetrahedron 1994, 50, 8929–8940. doi:10.1016/S0040-4020(01)85363-1 |
| 11. | Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G. Tetrahedron 2009, 65, 3502–3508. doi:10.1016/j.tet.2009.02.020 |
| 13. | Sarotti, A. M.; Spanevello, R. A.; Suárez, A. G. Org. Lett. 2006, 8, 1487–1490. doi:10.1021/ol0603099 |
| 16. | Sarotti, A. M.; Fernández, I.; Spanevello, R. A.; Sierra, M. Á.; Suárez, A. G. Org. Lett. 2008, 10, 3389–3392. doi:10.1021/ol801140g |
© 2016 Corne et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)








