Abstract
Four diastereoisomers of 2-fluorobicyclo[2.2.1]heptan-7-ols were computationally investigated by using quantum-chemical calculations, and their relative energies were analyzed on the basis of stereoelectronic interactions, particularly the presence or otherwise of the F∙∙∙HO intramolecular hydrogen bond in the syn-exo isomer. It was found through NBO and AIM analyses that such an interaction contributes to structural stabilization and that the 1hJF,H(O) coupling constant in the syn-exo isomer is modulated by the nF→σ*OH interaction, i.e., the quantum nature of the F∙∙∙HO hydrogen bond.
Graphical Abstract
Introduction
Intra- and intermolecular hydrogen bonds (HB) play an important role in determining the molecular arrangements and properties, as well as reactivity of a wide range of chemical and biological systems [1]. However, it has been argued that organic fluorine hardly ever participates in HB, due to the poor proton acceptor ability of the fluorine atom [2]; nevertheless, there are some instances of organofluorine compounds forming seven-membered hydrogen bonds [3], while the absence of HB in some monocyclic fluorohydrins has been shown to be due to geometric restrictions imposed by the ring size [4]. While structure 1 in Figure 1 exhibits a F∙∙∙HO intramolecular HB, structures 2, 3 and 4 do not experience such an interaction [5-8]. However, 2-fluorophenol (4) shows a through-space (TS) coupling constant 1TSJF,H(O) of ca. 5 Hz, which has been ascribed as being due to the overlap of electronic clouds between F and hydroxy H rather than to hydrogen bonding [8], while the corresponding SSCC in 8-fluoro-4-methyl-1-naphthol, which exhibits F∙∙∙HO intramolecular HB, is substantially higher, i.e., (−)28.4 Hz [9].
Figure 1: Some organofluorine compounds and the 2-fluorobicyclo[2.2.1]heptan-7-ols (5–8) theoretically studied in this work.
Figure 1: Some organofluorine compounds and the 2-fluorobicyclo[2.2.1]heptan-7-ols (5–8) theoretically studie...
In fact, the importance of NMR scalar spin–spin coupling constants (SSCCs) transmitted through hydrogen bonds emerged, fundamentally, from the observation of 1hJ15N,H and 2hJ15N,15N SSCCs for DNA and RNA molecular systems [10,11]. 19F is a suitable nucleus for NMR analysis, since it has spin 1/2, and thus, F∙∙∙HO intra/intermolecular HB in biological systems can be readily assessed through JF,H(O) SSCCs. This seems relevant because the replacement of a hydrogen by a fluorine atom in a molecule does not have a significant steric effect, but it suppresses adventitious metabolism, influences the pKa of functional groups, and alters solution conformation [12].
In this context, conformational screening and theoretical evaluation of 2-fluorobicyclo[2.2.1]heptan-7-ols (2-fluoronorbornan-7-ols, compounds 5–8 in Figure 1) represents an adequate approach to rationalize the role of F∙∙∙HO intra/intermolecular HB, since these model compounds are less flexible (easier to analyze) than others based on, e.g., the 2-fluoroethanol fragment, and allow the energetic comparison with a pool of diastereoisomers that do not experience such an interaction. Intramolecular interactions between vicinal F and OH groups have already been investigated in cyclic compounds (including aromatic rings) [4], and the present study extends such analysis to aliphatic compounds capable of forming six-membered rings through hydrogen bonding.
Results and Discussion
The hydroxy group of the 2-fluorobicyclo[2.2.1]heptan-7-ols undergoes rotation, giving rise to the stable conformers (energy minima) of the potential energy surfaces (PES) in Figure 2, which were obtained by computing the relative energies of 5–8 upon scanning of the H–O–C–C(CF) dihedral angle (θ) in steps of 10° at the HF/6-31g(d,p) level, using the Gaussian09 package of programs [13]. Each minimum was subsequently optimized at the MP2/aug-cc-pVDZ level, and the respective energies are given in Table 1, which shows that the conformer of 5 with the hydroxy hydrogen directed toward the fluorine atom (θ = 330.0°) is the most stable structure in the gas phase (this structure will be further referred to as the global minimum). This suggests that a F∙∙∙HO intramolecular HB is operating and governs the stability of 5; however, different organofluorine compounds with similar orientation of the hydroxy group do not exhibit such an interaction and are highly stable [6,8]. This can be either due to other attractive interactions present in the referred conformer or prevalent repulsive interactions (e.g., between fluorine and oxygen lone pairs) in the other conformer(s). In the present study, comparison of 5 with three diastereoisomers (6–8) gives insight into the role of F∙∙∙HO intramolecular HB for the conformer stabilization, since the simple observation that the conformational energy in 5 is ca. 2.9 kcal mol−1 does not warrant that F∙∙∙HO intramolecular HB is the dominating, or even an operating, factor of the conformational isomerism in 5.
Figure 2: Potential energy surfaces for the diastereoisomers of 2-fluorobicyclo[2.2.1]heptan-7-ols (5–8), obtained at the HF/6-31g(d,p) level, and the optimized minima at the MP2/aug-cc-pVDZ level (θ dihedral angles and relative energies, in kcal mol−1, in parenthesis).
Figure 2: Potential energy surfaces for the diastereoisomers of 2-fluorobicyclo[2.2.1]heptan-7-ols (5–8), obt...
Table 1: H–O–C–C(CF) dihedral angle (θ, in deg), relative energies, relative Lewis type energies, hyperconjugative energies, and nF→σ*OH interaction energies (in kcal mol−1).
| Diastereoisomer | θ | Erel | Erel (Lewis) | Ehyperconjugation | nF→σ*OH |
|---|---|---|---|---|---|
| 5 "syn-exo" | 181.0° | 2.92 | 9.7 | 444.0 | 0.0 |
| 5 "syn-exo" a | 330.0° | 0.00 | 6.9 | 438.3 | 4.0 |
| 6 "anti-exo" | 55.5° | 1.55 | 5.3 | 437.9 | 0.0 |
| 6 "anti-exo" | 182.0° | 0.31 | 0.7 | 434.6 | 0.0 |
| 6 "anti-exo" | 283.2° | 0.21 | 0.0 | 434.0 | 0.0 |
| 7 "syn-endo" | 72.4° | 1.40 | 0.7 | 434.0 | 0.0 |
| 7 "syn-endo" | 183.7° | 1.32 | 0.7 | 433.7 | 0.0 |
| 8 "anti-endo" | 53.7° | 2.26 | 7.7 | 439.7 | 0.0 |
| 8 "anti-endo" | 178.0° | 1.65 | 5.2 | 437.9 | 0.0 |
| 8 "anti-endo" | 288.2° | 1.60 | 4.7 | 437.4 | 0.0 |
aGlobal minimum.
Diastereoisomers with endo fluorine are all above 1 kcal mol−1 less stable than the global minimum, indicating that such an orientation is less favored than the exo one; this behavior is independent of the orientation of the hydroxy group, since F and OH neither attract nor repel each other in the F-endo orientation. However, anti-exo conformations can be used to account for the stability of the global minimum, since the orientation of their fluorine atoms is the same, and thus, the intramolecular interactions with the hydroxy group are expected to explain the energetic profile. In the gas phase, two anti-exo conformations are marginally less stable than the global minimum, indicating that F∙∙∙HO intramolecular HB is operating and stabilizing. The quantum nature of this interaction can be described by the hyperconjugative interaction nF→σ*OH [14], i.e., by the electron transfer from the nonbonding orbitals of fluorine to the symmetrically allowed vacant orbital σ*OH. Obviously, this spatial symmetry also appears for the bonding σOH orbital, giving rise to a repulsive nF/σOH interaction; the F∙∙∙HO intramolecular HB, an attractive interaction, would appear if the referred hyperconjugative interaction (plus the electrostatic nature of the Fδ−∙∙∙+δHO interaction) overrode the 4-electron/2-orbital interaction. Thus, the occurrence of the nF→σ*OH interaction, which can be numerically estimated from natural bond orbital (NBO) analysis [15], is a descriptor, but not sufficient evidence, that F∙∙∙HO intramolecular HB exists. It is worth mentioning that such an interaction was calculated to be 0.9 kcal mol−1 in the gas phase for 2-fluorophenol (4), which does not exhibit F∙∙∙HO intramolecular HB [8]. Indeed, this hyperconjugative interaction was calculated at the B3LYP/aug-cc-pVDZ level to be 4.0 kcal mol−1 for the global minimum (and zero for the other structures), while the most stable anti-exo structure is only 0.2 kcal mol−1 less stable than the global minimum; clearly, there is a competition between attractive nF→σ*OH and repulsive nF/σOH interactions in the global minimum, but its slightly higher stability compared to the anti-exo minimum indicates that the former interaction is prevalent.
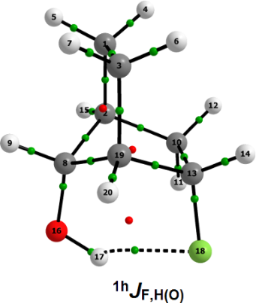
The F∙∙∙HO intramolecular HB in the global minimum was fully confirmed by Quantum Theory of AIM (QTAIM) analysis [16]. The QTAIM method is a rigorous electron density (ρ), interpretative methodology, which can define, unambiguously, atoms as they exist in molecules and the interactions between such atoms [16-18]. Even the weakest bonding interactions can be defined by the QTAIM through the so-called bond paths (BPs), that is, lines of maximum electron density linking neighboring nuclei of a molecular system in an equilibrium geometry, which, as repeatedly emphasized by Bader, is the sufficient and necessary condition for the definition of bonding between atoms [19-21]. According to Figure 3 and the QTAIM data of Table 2, the global minimum indeed experiences F∙∙∙HO intramolecular HB (parameters generated by using the other syn-exo conformer are taken as standard, because it cannot show HB), which is therefore the determining factor in its stability. Also, the stability and ionic character of the F∙∙∙HO intramolecular HB in the global minimum were confirmed by the low value of the ellipticity at the bond critical point (BCP, 0.04 au) and the |VC|/GC relationship at the BCP (VC and GC are the kinetic and potential energy values at the F∙∙∙HO HB BCP), respectively. The |VC|/GC parameter value is lower than 1 au (i.e., 0.973 au), and hence, the F∙∙∙HO intramolecular HB in the global minimum has an ionic character [22].
![[1860-5397-8-137-3]](/bjoc/content/figures/1860-5397-8-137-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: Molecular plots obtained by QTAIM for 5. Green points represent bond critical points (BCPs) and red ones represent ring critical points (RCPs).
Figure 3: Molecular plots obtained by QTAIM for 5. Green points represent bond critical points (BCPs) and red...
Table 2:
Electronic density (ρ) and its Laplacian () in the bond critical point (BCP) referring to the F∙∙∙HO intramolecular HB (HBCP), and the integrated properties on the H(O) atoms of the conformers of 5.
| Diastereoisomer | ρ |
|
q(H) | E(H) | M1(H) | V(H) | rH | ΔrHa | rF20 | ΔrF20a |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 (θ = 181.0°) | — | — | +0.605 | −0.3391 | 0.163 | 20.894 | — | — | — | — |
| 5 (global minimum) | 0.019 | +0.075 | +0.646 | −0.3209 | 0.129 | 14.671 | 0.76 | 0.49 | 1.27 | 0.40 |
aΔrX = rX − r0X, wherein r0X corresponds to the distance from the X nucleus (which is not involved in HB – atoms of 5 with θ = 181.0°) to the contour surface of constant 0.001 a.u., and rX corresponds to the distance from X to HBCP (obtained for the global minimum). r0H(O) = 1.25Å and r0F = 1.67Å in 5 (θ = 181.0°).
In fact, according to the NBO theory, the total energy of a molecule can be split into Lewis type interactions (basically steric interactions) and electron-transfer interactions (such as hyperconjugation); this can be achieved by deleting all interactions involving antibonding and Rydberg orbitals in a molecule and then computing the energy of this hypothetical system. Accordingly, the global minimum was found to be the most destabilized form in terms of steric effects (possibly because of the nF/σOH contribution), but it is greatly stabilized by hyperconjugative interactions, with special emphasis on the nF→σ*OH interaction (4.0 kcal mol−1).
Since the nF→σ*OH interaction prevails over the nF/σOH repulsion, the F∙∙∙HO intramolecular HB can be the main transmission mechanism of a through-space F–H(O) coupling constant (1hJF,H(O)). This can be important for monitoring fluorine-based interactions in biological systems and material sciences. The angular dependence of 1hJF,H(O) as a function of the nF→σ*OH interaction was theoretically evaluated at the BHandH/EPR-III level (which has shown to perform well in estimating 19F-based couplings [23]), and a high correlation was found (R2 = 0.97), indicating that such an interaction, and thus the F∙∙∙HO intramolecular HB forming a six-membered ring, modulates the 1hJF,H(O) SSCC (Figure 4), which is governed by the Fermi contact term. The SSCC amplitudes upon varying θ for the remaining diastereoisomers, are negligible (see Supporting Information File 1), as is the nF→σ*OH interaction, as expected; on the other hand, the calculated 1hJF,H(O) SSCC for the global minimum is significant (ca. −18 Hz, Table 3).
Figure 4: Angular dependence of 1hJF,H(O) and nF→σ*OH interaction in 5.
Figure 4: Angular dependence of 1hJF,H(O) and nF→σ*OH interaction in 5.
Table 3: Calculated F,H(O) SSCC for 5–8, and the corresponding terms contributing to the overall J (FC, Fermi contact; SD, spin dipolar; PSO, paramagnetic spin-orbit; DSO, diamagnetic spin-orbit), in hertz.
| Diastereoisomer | θ | FC | SD | PSO | DSO | Total J |
|---|---|---|---|---|---|---|
| 5 "syn-exo" | 181.0° | 0.67 | −0.02 | 1.28 | −1.47 | 0.46 |
| 5 "syn-exo" a | 330.0° | −17.68 | 1.41 | −5.74 | 3.902 | −18.10 |
| 6 "anti-exo" | 55.5° | 0.63 | −0.10 | 1.08 | −1.24 | 0.37 |
| 6 "anti-exo" | 182.0° | −0.11 | −0.01 | 0.89 | −1.00 | −0.24 |
| 6 "anti-exo" | 283.2° | 0.11 | −0.08 | 0.44 | −0.48 | −0.01 |
| 7 "syn-endo" | 72.4° | 0.14 | 0.06 | 0.61 | −1.13 | −0.32 |
| 7 "syn-endo" | 183.7° | −0.36 | 0.05 | 0.01 | −0.02 | −0.86 |
| 8 "anti-endo" | 53.7° | 2.92 | 0.01 | 1.05 | −1.41 | 2.57 |
| 8 "anti-endo" | 178.0° | −0.58 | −0.08 | 0.88 | −0.92 | −0.69 |
| 8 "anti-endo" | 288.2° | −0.01 | 0.18 | 0.62 | −1.06 | −0.28 |
aGlobal minimum.
The FC term, which dominates the 1hJF,H(O) coupling in 5, is transmitted mainly by more inner electrons than p-type ones, i.e., those with higher s % character; orbitals involved in hydrogen bonding exhibit large s % character [24]. The fluorine lone pairs (LPF) are involved in charge transfer toward the σ*OH orbital, and hence, the s % character of these lone pairs should indicate the establishment of F∙∙∙H–O HB and, consequently, a pathway for the 1hJF,H(O) coupling in 5. While attractive interactions, such as hydrogen bonding, are expected to increase the s % character of the interacting lone pair, repulsive interactions are supposed to decrease such an s % character [24]. Accordingly, a brief comparison of the s % character in 5–8 (Table 4), obtained from the NBO analysis at the B3LYP/aug-cc-pVDZ level, indicates that a fluorine lone pair (LPF(1)) is preponderantly involved in repulsive interactions (such as nF/σOH), while LPF(3) participates in interactions that are preponderantly attractive; summed up, the larger s % character of the nF lone pairs in the global minimum compared to the diastereoisomers that are not capable of exhibiting HB, indicates an overall (slight) attractive interaction between F and OH, in agreement with the small energy difference between the global minimum and the second-most stable structure (anti-exo, θ = 283.2°).
Table 4: The s % character of LPF in 5–8.
| Diastereoisomer | θ | LPF(1) | LPF(2) | LPF(3) |
|---|---|---|---|---|
| 5 "syn-exo" | 181.0° | 71.85% | 0.36% | 0.03% |
| 5 "syn-exo" a | 330.0° | 71.81% | 0.00% | 1.01% |
| 6 "anti-exo" | 55.5° | 72.38% | 0.12% | 0.02% |
| 6 "anti-exo" | 182.0° | 72.41% | 0.11% | 0.01% |
| 6 "anti-exo" | 283.2° | 72.43% | 0.13% | 0.01% |
| 7 "syn-endo" | 72.4° | 72.19% | 0.05% | 0.02% |
| 7 "syn-endo" | 183.7° | 72.17% | 0.04% | 0.02% |
| 8 "anti-endo" | 53.7° | 72.21% | 0.05% | 0.01% |
| 8 "anti-endo" | 178.0° | 72.13% | 0.06% | 0.01% |
| 8 "anti-endo" | 288.2° | 72.17% | 0.06% | 0.00% |
aGlobal minimum.
Conclusion
In summary, there is a competition between nF→σ*OH and nF/σOH interactions as driving forces of the conformational isomerism of 5, but the former is slightly dominant, modulates the 1hJF,OH SSCC in this aliphatic organofluorine compound, and is the main factor responsible for the large value of 1hJF,OH in the global minimum.
Supporting Information
Supporting Information contains experimental procedures for newly synthesized compounds and NMR spectra.
| Supporting Information File 1: Angular dependences of SSCCs and energies in 5–8. | ||
| Format: PDF | Size: 838.1 KB | Download |
References
-
Nudelman, N. S.; Alvaro, C. E. S. J. Phys. Org. Chem. 2011, 24, 1067–1071. doi:10.1002/poc.1832
Return to citation in text: [1] -
Dunitz, J. D.; Taylor, R. Chem.–Eur. J. 1997, 3, 89–98. doi:10.1002/chem.19970030115
Return to citation in text: [1] -
Fonseca, T. A. O.; Freitas, M. P.; Cormanich, R. A.; Ramalho, T. C.; Tormena, C. F.; Rittner, R. Beilstein J. Org. Chem. 2012, 8, 112–117. doi:10.3762/bjoc.8.12
Return to citation in text: [1] -
Cormanich, R. A.; Freitas, M. P.; Tormena, C. F.; Rittner, R. RSC Adv. 2012, 2, 4169–4174. doi:10.1039/c2ra00039c
Return to citation in text: [1] [2] -
Takemura, H.; Kaneko, M.; Sako, K.; Iwanaga, T. New J. Chem. 2009, 33, 2004–2006. doi:10.1039/b902203a
Return to citation in text: [1] -
Souza, F. R.; Freitas, M. P. Comput. Theor. Chem. 2011, 964, 155–159. doi:10.1016/j.comptc.2010.12.014
Return to citation in text: [1] [2] -
Senent, M. L.; Niño, A.; Muñoz-Caro, C.; Smeyers, Y. G.; Domínguez-Gómez, R.; Orza, J. M. J. Phys. Chem. A 2002, 106, 10673–10680. doi:10.1021/jp026542f
Return to citation in text: [1] -
Cormanich, R. A.; Moreira, M. A.; Freitas, M. P.; Ramalho, T. C.; Anconi, C. P. A.; Rittner, R.; Contreras, R. H.; Tormena, C. F. Magn. Reson. Chem. 2011, 49, 763–767. doi:10.1002/mrc.2838
Return to citation in text: [1] [2] [3] [4] -
Takemura, H.; Ueda, R.; Iwanaga, T. J. Fluorine Chem. 2009, 130, 684–688. doi:10.1016/j.jfluchem.2009.05.004
Return to citation in text: [1] -
Dingley, A. J.; Grzesiek, S. J. Am. Chem. Soc. 1998, 120, 8293–8297. doi:10.1021/ja981513x
Return to citation in text: [1] -
Pervushin, K.; Ono, A.; Fernández, C.; Szyperski, T.; Kainosho, M.; Wüthrich, K. Proc. Natl. Acad. Sci. U. S. A. 1998, 95, 14147–14151. doi:10.1073/pnas.95.24.14147
Return to citation in text: [1] -
O’Hagan, D. Chem. Soc. Rev. 2008, 37, 308–319. doi:10.1039/b711844a
Return to citation in text: [1] -
Gaussian, 09, Revision A.02; Gaussian, Inc.: Wallingford CT, 2009.
Return to citation in text: [1] -
Weinhold, F.; Klein, R. A. Mol. Phys. 2012, 110, 565–579. doi:10.1080/00268976.2012.661478
Return to citation in text: [1] -
NBO, Version 5.0, included in the Gaussian09 package of programs; Gaussian Inc: Wallingford, CT, 2009.
Return to citation in text: [1] -
Bader, R. F. W. Atoms in Molecules: A Quantum Theory; Clarendon: Oxford, 1990.
Return to citation in text: [1] [2] -
Bader, R. F. W. Chem. Rev. 1991, 91, 893–928. doi:10.1021/cr00005a013
Return to citation in text: [1] -
Bader, R. F. W. J. Phys. Chem. A 1998, 102, 7314–7323. doi:10.1021/jp981794v
Return to citation in text: [1] -
Bader, R. F. W. Chem.–Eur. J. 2006, 12, 2896–2901. doi:10.1002/chem.200501589
Return to citation in text: [1] -
Bader, R. F. W. J. Phys. Chem. A 2009, 113, 10391–10396. doi:10.1021/jp906341r
Return to citation in text: [1] -
Bader, R. F. W. J. Phys. Chem. A 2010, 114, 7431–7444. doi:10.1021/jp102748b
Return to citation in text: [1] -
Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. J. Chem. Phys. 2002, 117, 5529–5542. doi:10.1063/1.1501133
Return to citation in text: [1] -
Vilcachagua, J. D.; Ducati, L. C.; Rittner, R.; Contreras, R. H.; Tormena, C. F. J. Phys. Chem. A 2011, 115, 1272–1279. doi:10.1021/jp110290b
Return to citation in text: [1] -
Anizelli, P. R.; Favaro, D. C.; Contreras, R. H.; Tormena, C. F. J. Phys. Chem. A 2011, 115, 5684–5692. doi:10.1021/jp202592c
Return to citation in text: [1] [2]
| 22. | Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. J. Chem. Phys. 2002, 117, 5529–5542. doi:10.1063/1.1501133 |
| 16. | Bader, R. F. W. Atoms in Molecules: A Quantum Theory; Clarendon: Oxford, 1990. |
| 17. | Bader, R. F. W. Chem. Rev. 1991, 91, 893–928. doi:10.1021/cr00005a013 |
| 18. | Bader, R. F. W. J. Phys. Chem. A 1998, 102, 7314–7323. doi:10.1021/jp981794v |
| 19. | Bader, R. F. W. Chem.–Eur. J. 2006, 12, 2896–2901. doi:10.1002/chem.200501589 |
| 20. | Bader, R. F. W. J. Phys. Chem. A 2009, 113, 10391–10396. doi:10.1021/jp906341r |
| 21. | Bader, R. F. W. J. Phys. Chem. A 2010, 114, 7431–7444. doi:10.1021/jp102748b |
| 1. | Nudelman, N. S.; Alvaro, C. E. S. J. Phys. Org. Chem. 2011, 24, 1067–1071. doi:10.1002/poc.1832 |
| 5. | Takemura, H.; Kaneko, M.; Sako, K.; Iwanaga, T. New J. Chem. 2009, 33, 2004–2006. doi:10.1039/b902203a |
| 6. | Souza, F. R.; Freitas, M. P. Comput. Theor. Chem. 2011, 964, 155–159. doi:10.1016/j.comptc.2010.12.014 |
| 7. | Senent, M. L.; Niño, A.; Muñoz-Caro, C.; Smeyers, Y. G.; Domínguez-Gómez, R.; Orza, J. M. J. Phys. Chem. A 2002, 106, 10673–10680. doi:10.1021/jp026542f |
| 8. | Cormanich, R. A.; Moreira, M. A.; Freitas, M. P.; Ramalho, T. C.; Anconi, C. P. A.; Rittner, R.; Contreras, R. H.; Tormena, C. F. Magn. Reson. Chem. 2011, 49, 763–767. doi:10.1002/mrc.2838 |
| 8. | Cormanich, R. A.; Moreira, M. A.; Freitas, M. P.; Ramalho, T. C.; Anconi, C. P. A.; Rittner, R.; Contreras, R. H.; Tormena, C. F. Magn. Reson. Chem. 2011, 49, 763–767. doi:10.1002/mrc.2838 |
| 4. | Cormanich, R. A.; Freitas, M. P.; Tormena, C. F.; Rittner, R. RSC Adv. 2012, 2, 4169–4174. doi:10.1039/c2ra00039c |
| 16. | Bader, R. F. W. Atoms in Molecules: A Quantum Theory; Clarendon: Oxford, 1990. |
| 3. | Fonseca, T. A. O.; Freitas, M. P.; Cormanich, R. A.; Ramalho, T. C.; Tormena, C. F.; Rittner, R. Beilstein J. Org. Chem. 2012, 8, 112–117. doi:10.3762/bjoc.8.12 |
| 14. | Weinhold, F.; Klein, R. A. Mol. Phys. 2012, 110, 565–579. doi:10.1080/00268976.2012.661478 |
| 2. | Dunitz, J. D.; Taylor, R. Chem.–Eur. J. 1997, 3, 89–98. doi:10.1002/chem.19970030115 |
| 15. | NBO, Version 5.0, included in the Gaussian09 package of programs; Gaussian Inc: Wallingford, CT, 2009. |
| 24. | Anizelli, P. R.; Favaro, D. C.; Contreras, R. H.; Tormena, C. F. J. Phys. Chem. A 2011, 115, 5684–5692. doi:10.1021/jp202592c |
| 10. | Dingley, A. J.; Grzesiek, S. J. Am. Chem. Soc. 1998, 120, 8293–8297. doi:10.1021/ja981513x |
| 11. | Pervushin, K.; Ono, A.; Fernández, C.; Szyperski, T.; Kainosho, M.; Wüthrich, K. Proc. Natl. Acad. Sci. U. S. A. 1998, 95, 14147–14151. doi:10.1073/pnas.95.24.14147 |
| 6. | Souza, F. R.; Freitas, M. P. Comput. Theor. Chem. 2011, 964, 155–159. doi:10.1016/j.comptc.2010.12.014 |
| 8. | Cormanich, R. A.; Moreira, M. A.; Freitas, M. P.; Ramalho, T. C.; Anconi, C. P. A.; Rittner, R.; Contreras, R. H.; Tormena, C. F. Magn. Reson. Chem. 2011, 49, 763–767. doi:10.1002/mrc.2838 |
| 9. | Takemura, H.; Ueda, R.; Iwanaga, T. J. Fluorine Chem. 2009, 130, 684–688. doi:10.1016/j.jfluchem.2009.05.004 |
| 23. | Vilcachagua, J. D.; Ducati, L. C.; Rittner, R.; Contreras, R. H.; Tormena, C. F. J. Phys. Chem. A 2011, 115, 1272–1279. doi:10.1021/jp110290b |
| 8. | Cormanich, R. A.; Moreira, M. A.; Freitas, M. P.; Ramalho, T. C.; Anconi, C. P. A.; Rittner, R.; Contreras, R. H.; Tormena, C. F. Magn. Reson. Chem. 2011, 49, 763–767. doi:10.1002/mrc.2838 |
| 4. | Cormanich, R. A.; Freitas, M. P.; Tormena, C. F.; Rittner, R. RSC Adv. 2012, 2, 4169–4174. doi:10.1039/c2ra00039c |
| 24. | Anizelli, P. R.; Favaro, D. C.; Contreras, R. H.; Tormena, C. F. J. Phys. Chem. A 2011, 115, 5684–5692. doi:10.1021/jp202592c |
© 2012 de Rezende et al; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)








