Abstract
We used dynamic 1H NMR spectroscopic methods to examine the kinetics and thermodynamics of CH3CCl3 (2) entering and leaving the gated molecular basket 1. We found that the encapsulation is first-order in basket 1 and guest 2, while the decomplexation is zeroth-order in the guest. Importantly, the interchange mechanism in which a molecule of CH3CCl3 directly displaces the entrapped CH3CCl3 was not observed. Furthermore, the examination of the additivity of free energies characterizing the encapsulation process led to us to deduce that the revolving motion of the gates and in/out trafficking of guests is synchronized, yet still a function of the affinity of the guest for occupying the basket: Specifically, the greater the affinity of the guest for occupying the basket, the less effective the gates are in “sweeping” the guest as the gates undergo their revolving motion.
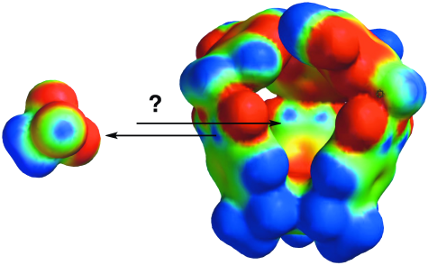
Graphical Abstract
Introduction
Covalent and self-assembled molecules with a natural cavity, i.e., molecular capsules [1,2], employ several mechanisms to trap and release guests capable of residing in their inner space [3-5]. The so-called “slippage” scenario [6], in which a guest makes its way to and from the host by forcing the expansion of its aperture [7], appears frequently. The “gating” scenario [8], on the other hand, includes a conformational change in the host to create an opening that is large enough for a guest to “squeeze” its way in or out of the host. In the case of self-assembled hosts, however, the slippage, gating and possible partial or full disassembly of the capsule constitute mechanistic alternatives for the exchange of guests [4]. In the last decade, we [9-14] and others [7,8,15-18] have studied gated molecular encapsulation in artificial and natural systems [19].
In particular, we designed gated molecular baskets (Figure 1) and employed both experimental and theoretical methods to gain an understanding of their mechanism of action [4]. These dynamic hosts comprise a semirigid platform with three aromatic gates appended to its rim through CH2 “hinges” (Figure 1). The gates were set to interact by hydrogen bonding to control the opening and closing of the basket and thereby the rate by which a guest enters or departs the cavity of the basket [12-14]. Indeed, the action mechanism of the basket has been addressed [14], yet the exact role of the gates in the process of the in/out guest exchange necessitates additional scrutiny. In particular, a careful inspection of the additivity of free energies [21] pertaining to the constrictive ΔG‡in/out and intrinsic ΔG° binding energies of the guests [11] as well as the racemization of the basket ΔG‡rac (i.e., opening and closing, see below in Figure 6) reveals a systematic disparity (ΔG° + ΔG‡rac + ΔG‡sterics ≠ ΔG‡out, see below in Figure 7). In order to address this conundrum, we have employed methods of experimental (dynamic NMR) and computational chemistry (steered molecular dynamics, SMD) to inspect the relationship between the gates revolving at the rim of the host and the in/out exchange of guests. The results of our study suggest that for guests with a greater propensity to occupy the interior of the basket (i.e., more negative ΔG°) the process of gating is poorly synchronized with the guest exchange. The gates undergo a revolving motion to sweep the space but are concurrently less effective in enforcing the ejection of the guest from the cavity. Moreover, the results of dynamic 1H NMR measurements of CH3CCl3 (2) entering and departing basket 1 (Figure 1) suggest the absence of an interchange mechanism [22] in which a molecule of CH3CCl3 directly displaces another CH3CCl3 residing in the interior of the gated basket.
![[1860-5397-8-9-1]](/bjoc/content/figures/1860-5397-8-9-1.jpg?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: Chemical structure of gated molecular basket 1 and 1,1,1-trichloroethane (2). Electrostatic potential surfaces of basket 1 and guest 2 were computed with Spartan (AM1) [20].
Figure 1: Chemical structure of gated molecular basket 1 and 1,1,1-trichloroethane (2). Electrostatic potenti...
Results and Discussion
The encapsulation stoichiometry and the intrinsic binding (ΔG°)
In an earlier study [13], we reported on the tendency of basket 1 to trap CH3CCl3 (2) as a guest, and we hereby elaborate on the equilibrium thermodynamics of the recognition event (Figure 2). The incremental addition of 2 to a CD2Cl2 solution of 1 (0.67 mM, 298.0 K) caused considerable 1H NMR chemical shifts of the resonances corresponding to the presence of the basket (Figure 2). At 298.0 K, the formation and degradation of [basket–CH3CCl3] complex was sufficiently fast on the “NMR time scale”: The nonlinear least-squares fitting of the binding isotherm to a 1:1 binding model provided Ka = 54 ± 1 M−1 (R2 = 0.998, Figure 2) [23].
![[1860-5397-8-9-2]](/bjoc/content/figures/1860-5397-8-9-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: (Left): 1H NMR spectra (400 MHZ, CD2Cl2) of 1 (0.67 mM) obtained upon incremental addition of 1,1,1-trichloroethane (2) (0.00–0.65 M) at 298.0 K. (Middle): Nonlinear least-squares fitting (SigmaPlot) of the N–H chemical shift of 1 as a function of the concentration of 2 gave Ka = 54 ± 1 M−1 at 298.0 K [23]. (Right): The van't Hoff plot was generated from variable temperature 1H NMR measurements (400 MHz, 180–250 K) of 1 (0.67 mM) containing CH3CCl3 (1.07 mM).
Figure 2: (Left): 1H NMR spectra (400 MHZ, CD2Cl2) of 1 (0.67 mM) obtained upon incremental addition of 1,1,1...
Indeed, the results of a variable temperature 1H NMR study (400 MHz, CD2Cl2) of 1 (0.67 mM) containing CH3CCl3 (2) (1.07 mM) was in line with the formation of the 1:1 complex; note that extrapolation of the fitted line gives Ka of 86 ± 16 M−1 at 298.0 K, which is akin to the value obtained in the titration experiment. Furthermore, the van't Hoff analysis of the 1H NMR data revealed that the encapsulation is also driven by enthalpy (ΔH° = −3.56 ± 0.06 kcal/mol, Figure 2). Indeed, the computed electrostatic potential surface (AM1, Spartan) [20] of guest 2 is complementary to the one corresponding to the concave interior of 1 (Figure 1). Furthermore, compound 2 (93 Å3, Spartan) occupies 42% of the inner space of 1 (221 ± 9 Å3) [11], which is close to the packing coefficient of liquids and thereby a good indicator of a stable assembly [24].
The rate law characterizing guest exchange and the constrictive binding (ΔG‡in/out)
We performed 1H,1H-EXSY [25] and selective inversion-transfer [26,27] NMR measurements (400 MHz, CD2Cl2) to examine the rate laws characterizing the trafficking of CH3CCl3 (2) to and from basket 1. At concentrations of CH3CCl3 as a guest comparable to those of host 1, the EXSY measurements (250.0 ± 0.1 K) allowed us to extract (MNova software) the magnetization rate coefficients k*in and k*out (Figure 3).
![[1860-5397-8-9-3]](/bjoc/content/figures/1860-5397-8-9-3.jpg?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: Chemically equivalent CH3 protons (black) in 1,1,1-trichloroethane (2) alter their magnetic environment from 2.70 ppm in bulk solvent to −2.45 ppm inside the basket.
Figure 3: Chemically equivalent CH3 protons (black) in 1,1,1-trichloroethane (2) alter their magnetic environ...
At higher concentrations of CH3CCl3 with respect to host 1, however, we noticed an intense T1 noise coinciding with the [CH3CCl3]out signal, thus preventing the accurate determination of the volume of the corresponding cross peak. Accordingly, we had to turn to selective inversion-transfer NMR measurements to obtain the values of k*in and k*out. The exchange rate constants k*in and k*out (characterizing the longitudinal magnetization of the hydrogen nuclei in CH3CCl3 altering the chemical/magnetic environment) are by the nature of the experiment pseudo-first-order in character (see below) [25,26].
On the basis of the reaction stoichiometry (Figure 2), we initially made the assumption that the entrapment is first-order in both [basket] and [CH3CCl3]. Accordingly, the rate of the forward reaction is given as:
As per the earlier discussion, the pseudo-first-order constant k*in describes the longitudinal magnetization of the hydrogen nuclei in CH3CCl3 transferring from the bulk solvent (δ = 2.70 ppm, Figure 3) to the interior of 1 (δ = −2.45 ppm, Figure 3).
Correspondingly, the rate of the forward reaction (entrapment) can be formulated as:
From Equation 1 and Equation 2, we furthermore derive:
If the proposed model is valid, then the experimentally determined k*in will be linearly proportional to the concentration of free basket 1. Indeed, when the value of k*in is plotted against the concentration of free basket 1, there is an apparent linear dependence, with the slope of the fitted curve kin = 2.1 ± 0.3 × 103 M−1·s−1 (at 250 ± 0.1 K, Figure 4). Using Equation 4, we derive Equation 5, which upon insertion into Equation 3 gives Equation 6:
This particular dependence suggests that k*in should be directly proportional to the concentration of the host–guest complex, [basket–CH3CCl3], but inversely proportional to the concentration of CH3CCl3. At higher concentrations of CH3CCl3, however, there should be a negligible variation in the concentration of basket–CH3CCl3 and the magnetization rate coefficient k*in becomes inversely proportional to the concentration of CH3CCl3.
![[1860-5397-8-9-4]](/bjoc/content/figures/1860-5397-8-9-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: Nonlinear least-squares fitting (SigmaPlot) of magnetization rate constants k*in (2-D EXSY, 250.0 ± 0.1 K) as a function of the concentration of the free basket to a linear function gives a slope of kin = 2.1 ± 0.3 × 103 M−1·s−1.
Figure 4: Nonlinear least-squares fitting (SigmaPlot) of magnetization rate constants k*in (2-D EXSY, 250.0 ±...
In accordance with this theoretical model, we completed a series of selective inversion-transfer [27] NMR measurements of 1 (1.65 mM) and CH3CCl3 (16–200 mM) in CD2Cl2 at 250.0 ± 0.1 K (Figure 5). In the experiment, the proton resonance corresponding to [CH3CCl3]out was selectively inverted, resulting in the perturbation of the longitudinal relaxation of both [CH3CCl3]out and [CH3CCl3]in due to chemical exchange over the course of variable delay time τ (180° x (selective) – τ – 90° x (nonselective) – τd). Upon the integration of both signals (Iin and Iout), we subjected the data to nonlinear least-squares fitting of Iin/out versus τ using the proposed solutions of the McConnell equations [27] describing the relaxation of the hydrogen nucleus residing in two environments (Figure 5A). For the fitting, the longitudinal relaxation rate (1/T1) of hydrogen nuclei in CH3CCl3 was determined separately by using a classical selective inversion-recovery NMR pulse sequence. When the experimental k*in was plotted against the equilibrium concentration of CH3CCl3, there indeed appeared a hyperbolic dependence (Figure 5B) in agreement with Equation 6 (k*in 1/[CH3CCl3]). The fitting of the data to Equation 6 was inaccurate as only a few experimental points characterize the dependence (Figure 5B), although computing kin from each data point would give a value of this coefficient (~2 × 103 M−1·s−1) similar to that determined in the EXSY experiment (Figure 4). In accordance with the 2-D EXSY and selective inversion-transfer results, we conclude that the entrapment is first-order in both basket 1 and guest 2.
![[1860-5397-8-9-5]](/bjoc/content/figures/1860-5397-8-9-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: (A): Nonlinear least-squares fitting of 1H NMR signal intensities (Iin/out) of [CH3CCl3]in/out as function of the time variable τ (250.0 ± 0.1 K) was completed with the assistance of the Bloch–McConnell equations [27,28] describing the relaxation of hydrogen nuclei in two different environments; in this particular experiment [basket]0 = 1.65 mM and [CH3CCl3]0 = 50.0 mM. Magnetization transfer rate coefficients k*in (B) and k*out (C) were further obtained [27,28] from selective inversion-transfer measurements and plotted as a function of the concentration of free CH3CCl3.
Figure 5: (A): Nonlinear least-squares fitting of 1H NMR signal intensities (Iin/out) of [CH3CCl3]in/out as f...
On the basis of the reaction stoichiometry (Figure 2), the rate law for 2 leaving the encapsulation complex can be described as:
Alternatively, the rate of the same process expressed through the NMR magnetization transfer rate coefficient k*out is:
As in the case above, the manipulation of Equation 7 and Equation 8 gives Equation 9:
In accordance with this theoretical model, we increased the concentration of guest 2 (16–200 mM) with respect to 1 (1.65 mM) and measured k*out using the selective inversion-transfer NMR pulse sequence. Markedly, there was essentially no interdependence between k*out (21 ± 3 s−1) and the concentration of guest 2 (Figure 5C); the curve indeed shows a small slope, but the intercept of 18.1 suggests that this is likely an artifact. 2-D EXSY measurements would give a rate coefficient k*out = 10 ± 0.1 s−1, which was also found to be independent of the external concentration of the basket/guest (Figure 4). The departure of CH3CCl3 from its complexed form [basket–CH3CCl3], therefore, follows a dissociative mechanism [4]. Notably, a molecule of solvent CD2Cl2 and not another CH3CCl3 (interchange mechanism) displaces the encapsulated guest. In fact, the inspection of CPK models as well as molecular dynamics studies (see below) revealed that the departure of CH3CCl3 (93 Å3) demands (a) “opening” of at least two gates, (b) disruption of internal N–H…N hydrogen bonds, and (c) distortion of the framework of the basket. We further reason that in the case of a direct exchange of two CH3CCl3 molecules, the departure of CH3CCl3 would create an empty host, and therefore vacuum, before another guest of the same kind can take its place. Note that two large compounds (overall ~186 Å3) cannot simultaneously occupy the interior of 1 (~220 Å3).
Computational examination of the in/out trafficking
To gain mechanistic insight into the departure of CH3CCl3 (2) from the interior of basket 1, we completed a series of steered molecular dynamics (SMD) simulations using the AMBER 10.0 suite of programs [29-32]. Without applying any external force on the entrapped CH3CCl3, we first found that this guest would, within 10 ns, adopt many positions inside host 1, although the one depicted in Figure 6A is obtained after 1 ns (Supporting Information File 1). The N–H…N hydrogen bond contacts along the top of the basket were also monitored throughout the 10 ns simulation. Importantly, the distance between each pair of amide-hydrogen and pyridine-nitrogen atoms was found to be invariant (~2 Å, see Supporting Information File 1).
![[1860-5397-8-9-6]](/bjoc/content/figures/1860-5397-8-9-6.jpg?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: (A) Four different trajectories were used for examining the departure of CH3CCl3 guest from basket 1 with steered molecular dynamics. (B) The variation in N–H…N and –C=O…O=C– distances during SMD simulation with CH3CCl3 being pulled on the side.
Figure 6: (A) Four different trajectories were used for examining the departure of CH3CCl3 guest from basket 1...
In addition, the width of each side aperture (the span between adjacent carbonyl oxygen atoms) also remained constant at ~6.3 Å throughout the simulation (Figure S3, see Supporting Information File 1). We then selected multiple trajectories for “pulling” the guest from the host (Figure 6A). Markedly, the departure of CH3CCl3 necessitated the cleavage of at least two intramolecular N–H…N hydrogen bonds in 1 (Figure 6B) with a simultaneous expansion of the host (Figure 6B). That is to say, the “slippage” of CH3CCl3 (with gates in the “closed” position) does not appear to be a viable mechanistic scenario. Note that our simulation did not include solvent molecules (CD2Cl2) displacing the entrapped CH3CCl3, as suggested by the kinetic study. The substitution of the guest by the solvent should perhaps cause an even greater distortion of the framework of the basket.
The revolving of the gates and the racemization of basket 1
The aromatic gates in basket 1 interact through hydrogen bonding, as exemplified by a large downfield shift of the signal corresponding to (O=C)N−H protons (δ = 11.6 ppm at 298.0 K, Figure 2) [13]. In addition, the aromatic gates are dynamic, each one revolving about its axis to give rise to two enantiomeric conformers 1A and 1B (Figure 7A). The interconversion kinetics of the 1A/B racemization can be followed by dynamic NMR spectroscopy in which a singlet corresponding to Ha/Hb nuclei at high temperatures is seen to split into two doublets at low temperatures. In particular, the revolving rate of the gates is temperature dependent, thereby governing the lifetime of Ha or Hb nuclei, each residing in a particular chemical environment (τ = 1/krac); the hydrogen nuclei are observed as separate resonances when τ >> 1/Δν(Ha/b) [33]. Accordingly, we performed the classical line-shape analysis of Ha/Hb resonances (WinDNMR-Pro software) to obtain the rate constants (krac) and corresponding activation energies ΔG‡rac characterizing the racemization of basket 1 (Figure 7B). Evidently, the rate at which the aromatic gates in 1 revolve is a function of the compound occupying the inner space: With CH3CCl3 the gates are less dynamic than with CD2Cl2 occupying the cavity (Figure 7B).
![[1860-5397-8-9-7]](/bjoc/content/figures/1860-5397-8-9-7.jpg?scale=2.0&max-width=1024&background=FFFFFF)
Figure 7: (A) The interconversion of conformational enantiomers 1A and 1B, having anticlockwise and clockwise senses in the orientation of the intramolecular N–H…N hydrogen bonds, contributes to the process of racemization, i.e., the opening and closing of the basket [13]. (B) Eyring plots describing the linear relationship between ln(krac/T) and temperature for basket 1 containing CH3CCl3 (black squares) and solvent CD2Cl2 (red triangles). The plots were generated from the results of the line-shape analysis (WinDNMR-Pro) of 1H NMR Ha/b signals of 1 (1.65 mM, CD2Cl2) at variable temperatures.
Figure 7: (A) The interconversion of conformational enantiomers 1A and 1B, having anticlockwise and clockwise...
On the action mechanism of the basket
Is there a relationship between the aromatic gates sweeping the space and guests trafficking to and from the basket [11]? That is to say, will the gates expel the entrapped guest each time that they alter their propeller-like orientation (Figure 8)? First, our kinetic measurements suggest that guest CH3CCl3 (2) enters basket 1 by substituting solvent (CD2Cl2) molecule(s), while exactly the opposite occurs during the dissociation (Figure 8). Given this exchange scenario, we deduce that 1A–CH3CCl3 shall transform into 1B–CH3CCl3 via intermediate 1–CD2Cl2 (Figure 8). That is, the formation of 1–CD2Cl2 from 1A–CH3CCl3 is accompanied by either reorientation or reinstatement of the gates, and therefore, there is an equal likelihood that 1–CD2Cl2 will yield 1A–CH3CCl3 or 1B–CH3CCl3 (Figure 8); this reasoning is also supported by the fact that the gates of the solvated basket revolve at a higher rate (Figure 7B). In accordance with such a racemization mechanism, we apply the statistical correction to the measured krac to obtain krac′ (krac′ = 2krac = 616 s−1, Figure 7B) [34]. This particular rate coefficient should more precisely describe the process of racemization.
![[1860-5397-8-9-8]](/bjoc/content/figures/1860-5397-8-9-8.jpg?scale=2.0&max-width=1024&background=FFFFFF)
Figure 8: The departure of CH3CCl3 from 1A–CH3CCl3 gives rise to the less stable 1–CD2Cl2, which upon entrapment of another CH3CCl3 gives either 1A–CH3CCl3 or 1B–CH3CCl3. The 1A/B–CH3CCl3 interconversion occurs with CH3CCl3 departing (BR1 mechanism) or remaining (BR2 mechanism) in the cavity.
Figure 8: The departure of CH3CCl3 from 1A–CH3CCl3 gives rise to the less stable 1–CD2Cl2, which upon entrapm...
One could describe the free energy characterizing the guest departure (ΔG‡out) as a linear combination of ΔG‡rac′ + ΔG° + ΔG‡sterics representing (1) the opening of the gates (ΔG‡rac′), (2) the decomplexation of the guest (ΔG°), and (3) the “slippage” of the guest while exiting the open host (ΔG‡sterics) [8,11,21,35]. The encapsulation kinetics is first-order in guest CH3CCl3 suggesting that this species creates van der Waals strain (friction) during the in/out trafficking, thereby justifying the use of the ΔG‡sterics term.
In addition, the decomplexation of CH3CCl3 follows a late transition state [14] whereby its affinity for populating the interior of the basket should decrease to a somewhat smaller value than described by ΔG°. Given the delicacy of the proposed partitioning, will the additivity of free energies and the relationship ΔG‡rac′ + ΔG° + ΔG‡sterics ~ ΔG‡out still hold?
When ΔG‡rac′ of 11.4 ± 0.1 kcal/mol (at 250.0 ± 0.1 K, Figure 7) is added to the intrinsic binding energy of CH3CCl3 (│ΔG°│ = 2.79 ± 0.09 kcal/mol at 250.0 ± 0.1 K, Figure 2), a value of 14.2 kcal/mol is obtained. Without even including ΔG‡sterics (as a positive number), there is an apparent disagreement between the sum value (≥14.2 kcal/mol) and the experimentally determined ΔG‡out = 13.4 ± 0.1 kcal/mol (from 2-D EXSY, kout = 10 ± 1 s−1). Is there a missing factor needed in order to understand this phenomenon?
In reality, when the internal hydrogen bonds are broken and the gates open up the guest does not have to depart the basket cavity. That is to say, the gates should be able to revolve to allow the interconversion of 1A–CH3CCl3 into 1B–CH3CCl3 without even ejecting the guest. Accordingly, we hereby propose that the conversion of 1A–CH3CCl3 into 1B–CH3CCl3 (i.e., racemization) occurs by two routes, BR1 and BR2, one with (BR1) and another without (BR2) the concomitant guest exchange (Figure 8).
It follows that, during the departure of CH3CCl3, the measured racemization of 1 (ΔGrac′) includes energetic contributions from two pathways (ΔG‡rac′ = ΔG‡BR1 + ΔG‡BR2) of which only BR1 should be incorporated in the additivity assessment. It is therefore convenient to partition the energetic contribution of the two “competing” BR1 and BR2 routes to ΔG‡rac′ (ΔG‡rac′ = ΔG‡BR1 + ΔG‡BR2) to corroborate fully the role of the gates. However, this is a difficult task, but for guest molecules holding strongly onto the basket (more negative ΔG°) there should be a greater contribution from the RG2 pathway during the racemization.
In one of our prior studies [13,14], we measured kinetic and thermodynamic parameters pertaining to the exchange of five isosteric (same-size) guests 3–7 to and from basket 1 (Figure 9). When ΔG‡rac′ + ΔG° is computed for each guest and the values plotted against ΔG‡out, a linear relationship appears (R2 = 0.99, Figure 9A). Note that ΔG‡sterics is not included in this analysis as it is unknown; however, we anticipate that the value of the parameter should show minimal fluctuations for the series of isosteric guests 3–7. Importantly, the greater the affinity of a particular guest for occupying the interior of the basket (ΔG°), the greater the deviation of the calculated ΔG‡rac′ + ΔG° (black line, Figure 9A) from the experimental ΔG‡out (red line, Figure 9A). The variation of ΔΔG = (ΔG‡rac′ + ΔG°) − ΔG‡out with intrinsic binding energies ΔG° of 3–7 is shown in Figure 9B. The trend is evident, supporting the notion that for guests having greater propensity to occupy the basket (ΔG°) the BR2 pathway is more greatly involved in the 1A–CH3CCl3/1B–CH3CCl3 racemization. As already discussed, the BR2 pathway contributes to the measured ΔG‡rac′, yet it is not involved in the exchange of guests.
![[1860-5397-8-9-9]](/bjoc/content/figures/1860-5397-8-9-9.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 9: (A): Kinetic and thermodynamic parameters [13,14] characterizing the departure of isosteric guests 3–7 from the basket. (B): The computed ΔΔG = (ΔG‡rac′ + ΔG°) − ΔG‡out is apparently a linear function of ΔG‡out.
Figure 9: (A): Kinetic and thermodynamic parameters [13,14] characterizing the departure of isosteric guests 3–7 fro...
Conclusion
Describing mechanisms by which dynamic hosts entrap/release guests is a challenging task necessitating experimental and computational scrutiny. Notably, one can use NMR spectroscopic methods for understanding the equilibrium kinetics characterizing the rate law of molecular encapsulation processes. Our study, accordingly, describes the rate law characterizing the encapsulation of guest CH3CCl3 by the gated basket 1. Importantly, the entrapment reaction is first-order in each compound, while the complex dissociation is zeroth-order in guest CH3CCl3. Furthermore, examination of the additivity of free energies corresponding to different molecular events can assist in the understanding of the operation of gated hosts and, in particular, can help to reveal the explicit role of the gates. On the basis of these results, we deduced that the synchronicity in the revolving motion of the gates and in/out trafficking of guests is a function of the affinity of the guest for occupying the gated basket. The greater the affinity, the less effective the gates are in “sweeping” the guest as the gates undergo their revolving motion. This result is important for exploring the utility of gating for controlling the outcome of chemical reactions occurring in confined space but also for the understanding of the effective conversion of energy at the molecular level and the preparation of molecular machines [36,37].
Experimental
Procedure for 2-D EXSY experiments [25]: A solution of basket 1 and guest 2 in CD2Cl2 (J. Young NMR tube) was cooled to 250.0 ± 0.1 K inside the NMR probe and allowed to equilibrate for 1.0 h. A series of gradient NOESY experiments was run with a relaxation delay of 5 × T1 and mixing times (τm) of 0 ms and three others ranging from 40 ms to 250 ms, such that the cross-peaks were clearly resolved; the spin–lattice relaxation time (T1 = 3.30 s) for the free guest was determined by performing a standard inversion-recovery pulse sequence with a relaxation delay (τd) of at least 5 × T1. Each of the 128 F1 increments represented the accumulation of at least two scans. The corresponding integrals were determined by using MNova software from Mestrelab Research, after phase and baseline corrections in both dimensions. The magnetization exchange rate constants (k*in and k*out) were, at each mixing time τm, calculated by using the EXSYCalc program (Mestrelab Research). The mean values of k*in and k*out are reported with the standard deviation as an experimental error.
Procedure for 1H-selective inversion-transfer experiments [27]: A solution of basket 1 and guest 2 in CD2Cl2 (J. Young NMR tube) was cooled to 250.0 ± 0.1 K inside the NMR probe and allowed to equilibrate for 1.0 h. The 1H spin–lattice relaxation time (T1 = 3.30 s) for the free guest was determined by a standard inversion-recovery pulse sequence with a relaxation delay (τd) of at least 5 × T1. By using a selective 1-D inversion-recovery pulse sequence [180° x (selective) – τ – 90° x (nonselective) – τd], 32 transients were obtained for each variable delay time (τ) with a relaxation delay (τd) of at least 5 × T1. The absolute integrals corresponding to encapsulated and free guest molecules were, at each mixing time, determined by using TopSpin software from Bruker, and the resulting data was fitted by using the two-site exchange equations described by Led et al. [27] to obtain magnetization exchange rate constants k*in and k*out.
Supporting Information
Supporting Information contains details of the computational studies.
| Supporting Information File 1: Details of the computational studies. | ||
| Format: PDF | Size: 1.3 MB | Download |
References
-
Badjić, J. D.; Stojanović, S.; Ruan, Y. Adv. Phys. Org. Chem. 2011, 45, 1. doi:10.1016/B978-0-12-386047-7.00001-1
Return to citation in text: [1] -
Hof, F.; Craig, S. L.; Nuckolls, C.; Rebek, J., Jr. Angew. Chem., Int. Ed. 2002, 41, 1488. doi:10.1002/1521-3773(20020503)41:9<1488::AID-ANIE1488>3.0.CO;2-G
Return to citation in text: [1] -
Palmer, L. C.; Rebek, J., Jr. Org. Biomol. Chem. 2004, 2, 3051. doi:10.1039/b412510j
Return to citation in text: [1] -
Rieth, S.; Hermann, K.; Wang, B.-Y.; Badjić, J. D. Chem. Soc. Rev. 2011, 40, 1609. doi:10.1039/c005254j
Return to citation in text: [1] [2] [3] [4] -
Pluth, M. D.; Raymond, K. N. Chem. Soc. Rev. 2007, 36, 161. doi:10.1039/b603168b
Return to citation in text: [1] -
Davis, A. V.; Raymond, K. N. J. Am. Chem. Soc. 2005, 127, 7912. doi:10.1021/ja051037s
Return to citation in text: [1] -
Raymo, F. M.; Houk, K. N.; Stoddart, J. F. J. Am. Chem. Soc. 1998, 120, 9318. doi:10.1021/ja9806229
Return to citation in text: [1] [2] -
Houk, K. N.; Nakamura, K.; Sheu, C.; Keating, A. E. Science 1996, 273, 627. doi:10.1126/science.273.5275.627
Return to citation in text: [1] [2] [3] -
Maslak, V.; Yan, Z.; Xia, S.; Gallucci, J.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2006, 128, 5887. doi:10.1021/ja060534l
Return to citation in text: [1] -
Wang, B.-Y.; Bao, X.; Stojanovic, S.; Hadad, C. M.; Badjić, J. D. Org. Lett. 2008, 10, 5361. doi:10.1021/ol802199t
Return to citation in text: [1] -
Wang, B.-Y.; Bao, X.; Yan, Z.; Maslak, V.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2008, 130, 15127. doi:10.1021/ja8041977
Return to citation in text: [1] [2] [3] [4] [5] -
Wang, B.-Y.; Rieth, S.; Badjić, J. D. J. Am. Chem. Soc. 2009, 131, 7250. doi:10.1021/ja9023868
Return to citation in text: [1] [2] -
Rieth, S.; Badjić, J. D. Chem.–Eur. J. 2011, 17, 2562. doi:10.1002/chem.201003138
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] -
Rieth, S.; Bao, X.; Wang, B.-Y.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2010, 132, 773. doi:10.1021/ja908436c
Return to citation in text: [1] [2] [3] [4] [5] [6] -
Helgeson, R. C.; Hayden, A. E.; Houk, K. N. J. Org. Chem. 2010, 75, 570. doi:10.1021/jo9012496
Return to citation in text: [1] -
Sheu, C.; Houk, K. N. J. Am. Chem. Soc. 1996, 118, 8056. doi:10.1021/ja9535423
Return to citation in text: [1] -
Wang, X.; Houk, K. N. Org. Lett. 1999, 1, 591. doi:10.1021/ol9900820
Return to citation in text: [1] -
Hooley, R. J.; Van Anda, H. J.; Rebek, J., Jr. J. Am. Chem. Soc. 2006, 128, 3894. doi:10.1021/ja058727g
Return to citation in text: [1] -
Zhou, H.-X.; McCammon, J. A. Trends Biochem. Sci. 2010, 35, 179. doi:10.1016/j.tibs.2009.10.007
Return to citation in text: [1] -
Kamieth, M.; Klärner, F.-G.; Diederich, F. Angew. Chem., Int. Ed. 1998, 37, 3303. doi:10.1002/(SICI)1521-3773(19981217)37:23<3303::AID-ANIE3303>3.0.CO;2-T
Return to citation in text: [1] [2] -
Dill, K. A. J. Biol. Chem. 1997, 272, 701. doi:10.1074/jbc.272.2.701
Return to citation in text: [1] [2] -
Craig, S. L.; Lin, S.; Chen, J.; Rebek, J., Jr. J. Am. Chem. Soc. 2002, 124, 8780. doi:10.1021/ja025672z
Return to citation in text: [1] -
Wilcox, C. S. In Frontiers in supramolecular organic chemistry and photochemistry; Schneider, H.-J; Dürr, H., Eds.; VCH: Weinheim, Germany, 1991; pp 123 ff.
Return to citation in text: [1] [2] -
Mecozzi, S.; Rebek, J., Jr. Chem.–Eur. J. 1998, 4, 1016. doi:10.1002/(SICI)1521-3765(19980615)4:6<1016::AID-CHEM1016>3.0.CO;2-B
Return to citation in text: [1] -
Perrin, C. L.; Dwyer, T. J. Chem. Rev. 1990, 90, 935. doi:10.1021/cr00104a002
Return to citation in text: [1] [2] [3] -
Lian, L. Y. In NMR of macromolecules : a practical approach; Roberts, G. C. K., Ed.; IRL Press: Oxford, 1993; pp 153 ff.
Return to citation in text: [1] [2] -
Led, J. J.; Gesmar, H.; Abildgaard, F. Methods Enzymol. 1989, 176, 311. doi:10.1016/0076-6879(89)76017-1
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] -
Hansen, D. F.; Led, J. J. J. Magn. Reson. 2003, 163, 215. doi:10.1016/S1090-7807(03)00062-4
Return to citation in text: [1] [2] -
Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M. C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; Caldwell, J.; Wang, J.; Kollman, P. J. Comput. Chem. 2003, 24, 1999. doi:10.1002/jcc.10349
Return to citation in text: [1] -
Wang, J.; Wolf, R. M.; Caldwell, J. W.; Kollman, P. A.; Case, D. A. J. Comput. Chem. 2004, 25, 1157. doi:10.1002/jcc.20035
Return to citation in text: [1] -
Isralewitz, B.; Gao, M.; Schulten, K. Curr. Opin. Struct. Biol. 2001, 11, 224. doi:10.1016/S0959-440X(00)00194-9
Return to citation in text: [1] -
Sotomayor, M.; Schulten, K. Science 2007, 316, 1144. doi:10.1126/science.1137591
Return to citation in text: [1] -
Sandström, J. Dynamic NMR Spectroscopy; Academic Press: London, 1982.
Return to citation in text: [1] -
Bao, X.; Rieth, S.; Stojanović, S.; Hadad, C. M.; Badjić, J. D. Angew. Chem., Int. Ed. 2010, 49, 4816. doi:10.1002/anie.201000656
Return to citation in text: [1] -
Christensen, T.; Gooden, D. M.; Kung, J. E.; Toone, E. J. J. Am. Chem. Soc. 2003, 125, 7357. doi:10.1021/ja021240c
Return to citation in text: [1] -
Northrop, B. H.; Braunschweig, A. B.; Mendes, P. M.; Dichtel, R. W.; Stoddart, J. F. Molecular Machines. In Handbook of Nanoscience, Engineering, and Technology, 2nd ed.; Goddard, W. A.; Brenner, D. W.; Lyshevski, S. E.; Iafrate, G. J., Eds.; CRC Press: Boca Raton, 2007; 11-1–11-50.
Return to citation in text: [1] -
Saha, S.; Stoddart, J. F. Molecular Motors and Muscles. In Functional Organic Materials; Müller, T. J. J.; Bunz, U. H. F., Eds.; Wiley-VCH: Weinheim, Germany, 2007; pp 295 ff.
Return to citation in text: [1]
| 27. | Led, J. J.; Gesmar, H.; Abildgaard, F. Methods Enzymol. 1989, 176, 311. doi:10.1016/0076-6879(89)76017-1 |
| 28. | Hansen, D. F.; Led, J. J. J. Magn. Reson. 2003, 163, 215. doi:10.1016/S1090-7807(03)00062-4 |
| 27. | Led, J. J.; Gesmar, H.; Abildgaard, F. Methods Enzymol. 1989, 176, 311. doi:10.1016/0076-6879(89)76017-1 |
| 28. | Hansen, D. F.; Led, J. J. J. Magn. Reson. 2003, 163, 215. doi:10.1016/S1090-7807(03)00062-4 |
| 4. | Rieth, S.; Hermann, K.; Wang, B.-Y.; Badjić, J. D. Chem. Soc. Rev. 2011, 40, 1609. doi:10.1039/c005254j |
| 1. | Badjić, J. D.; Stojanović, S.; Ruan, Y. Adv. Phys. Org. Chem. 2011, 45, 1. doi:10.1016/B978-0-12-386047-7.00001-1 |
| 2. | Hof, F.; Craig, S. L.; Nuckolls, C.; Rebek, J., Jr. Angew. Chem., Int. Ed. 2002, 41, 1488. doi:10.1002/1521-3773(20020503)41:9<1488::AID-ANIE1488>3.0.CO;2-G |
| 8. | Houk, K. N.; Nakamura, K.; Sheu, C.; Keating, A. E. Science 1996, 273, 627. doi:10.1126/science.273.5275.627 |
| 22. | Craig, S. L.; Lin, S.; Chen, J.; Rebek, J., Jr. J. Am. Chem. Soc. 2002, 124, 8780. doi:10.1021/ja025672z |
| 8. | Houk, K. N.; Nakamura, K.; Sheu, C.; Keating, A. E. Science 1996, 273, 627. doi:10.1126/science.273.5275.627 |
| 11. | Wang, B.-Y.; Bao, X.; Yan, Z.; Maslak, V.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2008, 130, 15127. doi:10.1021/ja8041977 |
| 21. | Dill, K. A. J. Biol. Chem. 1997, 272, 701. doi:10.1074/jbc.272.2.701 |
| 35. | Christensen, T.; Gooden, D. M.; Kung, J. E.; Toone, E. J. J. Am. Chem. Soc. 2003, 125, 7357. doi:10.1021/ja021240c |
| 7. | Raymo, F. M.; Houk, K. N.; Stoddart, J. F. J. Am. Chem. Soc. 1998, 120, 9318. doi:10.1021/ja9806229 |
| 20. | Kamieth, M.; Klärner, F.-G.; Diederich, F. Angew. Chem., Int. Ed. 1998, 37, 3303. doi:10.1002/(SICI)1521-3773(19981217)37:23<3303::AID-ANIE3303>3.0.CO;2-T |
| 14. | Rieth, S.; Bao, X.; Wang, B.-Y.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2010, 132, 773. doi:10.1021/ja908436c |
| 6. | Davis, A. V.; Raymond, K. N. J. Am. Chem. Soc. 2005, 127, 7912. doi:10.1021/ja051037s |
| 11. | Wang, B.-Y.; Bao, X.; Yan, Z.; Maslak, V.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2008, 130, 15127. doi:10.1021/ja8041977 |
| 3. | Palmer, L. C.; Rebek, J., Jr. Org. Biomol. Chem. 2004, 2, 3051. doi:10.1039/b412510j |
| 4. | Rieth, S.; Hermann, K.; Wang, B.-Y.; Badjić, J. D. Chem. Soc. Rev. 2011, 40, 1609. doi:10.1039/c005254j |
| 5. | Pluth, M. D.; Raymond, K. N. Chem. Soc. Rev. 2007, 36, 161. doi:10.1039/b603168b |
| 11. | Wang, B.-Y.; Bao, X.; Yan, Z.; Maslak, V.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2008, 130, 15127. doi:10.1021/ja8041977 |
| 34. | Bao, X.; Rieth, S.; Stojanović, S.; Hadad, C. M.; Badjić, J. D. Angew. Chem., Int. Ed. 2010, 49, 4816. doi:10.1002/anie.201000656 |
| 19. | Zhou, H.-X.; McCammon, J. A. Trends Biochem. Sci. 2010, 35, 179. doi:10.1016/j.tibs.2009.10.007 |
| 12. | Wang, B.-Y.; Rieth, S.; Badjić, J. D. J. Am. Chem. Soc. 2009, 131, 7250. doi:10.1021/ja9023868 |
| 13. | Rieth, S.; Badjić, J. D. Chem.–Eur. J. 2011, 17, 2562. doi:10.1002/chem.201003138 |
| 14. | Rieth, S.; Bao, X.; Wang, B.-Y.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2010, 132, 773. doi:10.1021/ja908436c |
| 7. | Raymo, F. M.; Houk, K. N.; Stoddart, J. F. J. Am. Chem. Soc. 1998, 120, 9318. doi:10.1021/ja9806229 |
| 8. | Houk, K. N.; Nakamura, K.; Sheu, C.; Keating, A. E. Science 1996, 273, 627. doi:10.1126/science.273.5275.627 |
| 15. | Helgeson, R. C.; Hayden, A. E.; Houk, K. N. J. Org. Chem. 2010, 75, 570. doi:10.1021/jo9012496 |
| 16. | Sheu, C.; Houk, K. N. J. Am. Chem. Soc. 1996, 118, 8056. doi:10.1021/ja9535423 |
| 17. | Wang, X.; Houk, K. N. Org. Lett. 1999, 1, 591. doi:10.1021/ol9900820 |
| 18. | Hooley, R. J.; Van Anda, H. J.; Rebek, J., Jr. J. Am. Chem. Soc. 2006, 128, 3894. doi:10.1021/ja058727g |
| 14. | Rieth, S.; Bao, X.; Wang, B.-Y.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2010, 132, 773. doi:10.1021/ja908436c |
| 13. | Rieth, S.; Badjić, J. D. Chem.–Eur. J. 2011, 17, 2562. doi:10.1002/chem.201003138 |
| 9. | Maslak, V.; Yan, Z.; Xia, S.; Gallucci, J.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2006, 128, 5887. doi:10.1021/ja060534l |
| 10. | Wang, B.-Y.; Bao, X.; Stojanovic, S.; Hadad, C. M.; Badjić, J. D. Org. Lett. 2008, 10, 5361. doi:10.1021/ol802199t |
| 11. | Wang, B.-Y.; Bao, X.; Yan, Z.; Maslak, V.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2008, 130, 15127. doi:10.1021/ja8041977 |
| 12. | Wang, B.-Y.; Rieth, S.; Badjić, J. D. J. Am. Chem. Soc. 2009, 131, 7250. doi:10.1021/ja9023868 |
| 13. | Rieth, S.; Badjić, J. D. Chem.–Eur. J. 2011, 17, 2562. doi:10.1002/chem.201003138 |
| 14. | Rieth, S.; Bao, X.; Wang, B.-Y.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2010, 132, 773. doi:10.1021/ja908436c |
| 29. | Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M. C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; Caldwell, J.; Wang, J.; Kollman, P. J. Comput. Chem. 2003, 24, 1999. doi:10.1002/jcc.10349 |
| 30. | Wang, J.; Wolf, R. M.; Caldwell, J. W.; Kollman, P. A.; Case, D. A. J. Comput. Chem. 2004, 25, 1157. doi:10.1002/jcc.20035 |
| 31. | Isralewitz, B.; Gao, M.; Schulten, K. Curr. Opin. Struct. Biol. 2001, 11, 224. doi:10.1016/S0959-440X(00)00194-9 |
| 32. | Sotomayor, M.; Schulten, K. Science 2007, 316, 1144. doi:10.1126/science.1137591 |
| 4. | Rieth, S.; Hermann, K.; Wang, B.-Y.; Badjić, J. D. Chem. Soc. Rev. 2011, 40, 1609. doi:10.1039/c005254j |
| 4. | Rieth, S.; Hermann, K.; Wang, B.-Y.; Badjić, J. D. Chem. Soc. Rev. 2011, 40, 1609. doi:10.1039/c005254j |
| 13. | Rieth, S.; Badjić, J. D. Chem.–Eur. J. 2011, 17, 2562. doi:10.1002/chem.201003138 |
| 23. | Wilcox, C. S. In Frontiers in supramolecular organic chemistry and photochemistry; Schneider, H.-J; Dürr, H., Eds.; VCH: Weinheim, Germany, 1991; pp 123 ff. |
| 13. | Rieth, S.; Badjić, J. D. Chem.–Eur. J. 2011, 17, 2562. doi:10.1002/chem.201003138 |
| 13. | Rieth, S.; Badjić, J. D. Chem.–Eur. J. 2011, 17, 2562. doi:10.1002/chem.201003138 |
| 14. | Rieth, S.; Bao, X.; Wang, B.-Y.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2010, 132, 773. doi:10.1021/ja908436c |
| 23. | Wilcox, C. S. In Frontiers in supramolecular organic chemistry and photochemistry; Schneider, H.-J; Dürr, H., Eds.; VCH: Weinheim, Germany, 1991; pp 123 ff. |
| 13. | Rieth, S.; Badjić, J. D. Chem.–Eur. J. 2011, 17, 2562. doi:10.1002/chem.201003138 |
| 14. | Rieth, S.; Bao, X.; Wang, B.-Y.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2010, 132, 773. doi:10.1021/ja908436c |
| 36. | Northrop, B. H.; Braunschweig, A. B.; Mendes, P. M.; Dichtel, R. W.; Stoddart, J. F. Molecular Machines. In Handbook of Nanoscience, Engineering, and Technology, 2nd ed.; Goddard, W. A.; Brenner, D. W.; Lyshevski, S. E.; Iafrate, G. J., Eds.; CRC Press: Boca Raton, 2007; 11-1–11-50. |
| 37. | Saha, S.; Stoddart, J. F. Molecular Motors and Muscles. In Functional Organic Materials; Müller, T. J. J.; Bunz, U. H. F., Eds.; Wiley-VCH: Weinheim, Germany, 2007; pp 295 ff. |
| 27. | Led, J. J.; Gesmar, H.; Abildgaard, F. Methods Enzymol. 1989, 176, 311. doi:10.1016/0076-6879(89)76017-1 |
| 27. | Led, J. J.; Gesmar, H.; Abildgaard, F. Methods Enzymol. 1989, 176, 311. doi:10.1016/0076-6879(89)76017-1 |
| 26. | Lian, L. Y. In NMR of macromolecules : a practical approach; Roberts, G. C. K., Ed.; IRL Press: Oxford, 1993; pp 153 ff. |
| 27. | Led, J. J.; Gesmar, H.; Abildgaard, F. Methods Enzymol. 1989, 176, 311. doi:10.1016/0076-6879(89)76017-1 |
| 25. | Perrin, C. L.; Dwyer, T. J. Chem. Rev. 1990, 90, 935. doi:10.1021/cr00104a002 |
| 26. | Lian, L. Y. In NMR of macromolecules : a practical approach; Roberts, G. C. K., Ed.; IRL Press: Oxford, 1993; pp 153 ff. |
| 24. | Mecozzi, S.; Rebek, J., Jr. Chem.–Eur. J. 1998, 4, 1016. doi:10.1002/(SICI)1521-3765(19980615)4:6<1016::AID-CHEM1016>3.0.CO;2-B |
| 27. | Led, J. J.; Gesmar, H.; Abildgaard, F. Methods Enzymol. 1989, 176, 311. doi:10.1016/0076-6879(89)76017-1 |
| 25. | Perrin, C. L.; Dwyer, T. J. Chem. Rev. 1990, 90, 935. doi:10.1021/cr00104a002 |
| 20. | Kamieth, M.; Klärner, F.-G.; Diederich, F. Angew. Chem., Int. Ed. 1998, 37, 3303. doi:10.1002/(SICI)1521-3773(19981217)37:23<3303::AID-ANIE3303>3.0.CO;2-T |
| 25. | Perrin, C. L.; Dwyer, T. J. Chem. Rev. 1990, 90, 935. doi:10.1021/cr00104a002 |
| 11. | Wang, B.-Y.; Bao, X.; Yan, Z.; Maslak, V.; Hadad, C. M.; Badjić, J. D. J. Am. Chem. Soc. 2008, 130, 15127. doi:10.1021/ja8041977 |
| 27. | Led, J. J.; Gesmar, H.; Abildgaard, F. Methods Enzymol. 1989, 176, 311. doi:10.1016/0076-6879(89)76017-1 |
© 2012 Hermann et al; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)








