Abstract
Two novel tetrafluorinated 1,5-benzodiazepinones were synthesized and their X-ray structures determined. 6,7,8,9-Tetrafluoro-4-methyl-1,3-dihydro-2H-1,5-benzodiazepin-2-one crystallizes in the monoclinic P21/c space group and 6,7,8,9-tetrafluoro-1,4-dimethyl-1,3-dihydro-2H-1,5-benzodiazepin-2-one in the triclinic P−1 space group. Density functional theory studies at the B3LYP/6-311++G(d,p) level were carried out on these compounds and on four non-fluorinated derivatives, allowing to calculate geometries, tautomeric energies and ring-inversion barriers, that were compared with the experimental results obtained by static and dynamic NMR in solution and in solid state.
Graphical Abstract
Introduction
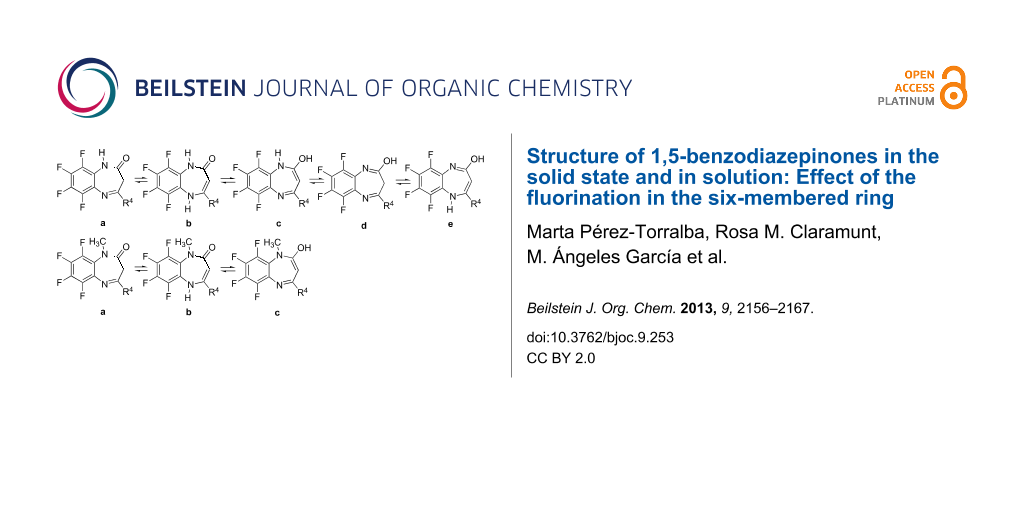
In our previous paper [1] we already reported the relevance of 1,5-benzodiazepine derivatives in central nervous system pathologies as well as for other applications in medicinal chemistry [2-6], the most important is clobazam (7-chloro-1-methyl-5-phenyl-1H-1,5-benzodiazepine-2,4(3H,5H)-dione, Figure 1). As a continuation of our research program on the synthesis, spectroscopic and biological properties of 1,5-benzodiazepine derivatives as well as their calculated parameters, we report in the present publication the experimental and theoretical studies of 1,5-benzodiazepinones 1–6; note that only compounds 1 and 2 are new; for compounds 3–6 we used literature data together with new computational results.
Figure 1: The six 1,5-benzodiazepinones discussed in this paper together with clobazam.
Figure 1: The six 1,5-benzodiazepinones discussed in this paper together with clobazam.
Results and Discussion
Synthesis
6,7,8,9-Tetrafluoro-4-methyl-1,3-dihydro-2H-1,5-benzodiazepin-2-one (1) was prepared in 63% yield by the reaction of 1,2-diamino-3,4,5,6-tetrafluorobenzene with ethyl acetylacetate (ethyl 3-oxobutanoate) following the literature procedure to prepare 3 [7] (Scheme 1). Further treatment with iodomethane under basic conditions afforded 6,7,8,9-tetrafluoro-1,4-dimethyl-1,3-dihydro-2H-1,5-benzodiazepin-2-one (2) in 80% yield.
Scheme 1: Synthesis of compounds 1 and 2.
Scheme 1: Synthesis of compounds 1 and 2.
Geometries
The geometries of two related structures together with their codes as reported in the Cambridge Structural Database [8,9] are shown in Figure 2.
![[1860-5397-9-253-2]](/bjoc/content/figures/1860-5397-9-253-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: The X-ray structures of 3a (TUPSAZ), 5a (EFARUA). In TUPSAZ there is a disordered water molecule.
Figure 2: The X-ray structures of 3a (TUPSAZ), 5a (EFARUA). In TUPSAZ there is a disordered water molecule.
Compound 1 crystallizes in the monoclinic P21/c space group containing one molecule per asymmetric unit (Figure 3; the numbering used in the crystallographic part is different from that of Figure 1). The bonding distances and angles agree with the electronic distribution according to one amide group on the C1 atom and one double bond, C3–N2, (tautomer a in Figure 7). The molecule is not planar due to the folding of the seven-membered ring with C1, C2 and C3 out of the plane defined by the aromatic ring and the nitrogen atoms. The dihedral angles between this plane and those formed by the C1N1O1 and N2C3C8 atoms are 35.4(2)º and 41.7(2)º, respectively.
![[1860-5397-9-253-3]](/bjoc/content/figures/1860-5397-9-253-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: ORTEP plot (30% probability) of 1, showing the X-ray labeling of the asymmetric unit.
Figure 3: ORTEP plot (30% probability) of 1, showing the X-ray labeling of the asymmetric unit.
These molecules are linked forming dimers by symmetric hydrogen bonds between the amide group and the carbonyl oxygen atom of an adjacent one (distances N1H1···O1’ 1.932(2) Å and N1···O1’ 2.877(2) Å; angle NHO 162.7(1)º). These dimers interact by double intermolecular F–F contacts between the F5 of a molecule and the F6 of a neighboring one (distance 2.875(2) Å) giving rise to a zigzag chain in the [10-1] direction (Figure 4). These chains are stacked by a partial π–π overlapping between the aromatic rings with a shortest distance of 3.19(1) Å.
![[1860-5397-9-253-4]](/bjoc/content/figures/1860-5397-9-253-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: View of the zigzag chain formed in 1, showing the H-bond and F–F interactions.
Figure 4: View of the zigzag chain formed in 1, showing the H-bond and F–F interactions.
Compound 2 crystallizes in the triclinic P–1 space group containing one molecule per asymmetric unit (Figure 5). As for compound 1, the molecular geometry corresponds to tautomer a. The seven-membered ring is also folded with dihedral angles between the aromatic ring and C1N1O1 of 44.1(3)º and with N2C3C8 of 43.2(3)º. This higher values compared to compound 1 indicate a greater deformation in the seven-membered ring owing to the presence of the N-methyl substituent.
![[1860-5397-9-253-5]](/bjoc/content/figures/1860-5397-9-253-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: ORTEP plot (20% probability) of 2, showing the X-ray labeling of the asymmetric unit.
Figure 5: ORTEP plot (20% probability) of 2, showing the X-ray labeling of the asymmetric unit.
The N-methylation prevents the dimerization by hydrogen bonding leading to a very different packing. Therefore, the most significant intermolecular interaction is the F–F contact between the F4 and F7 atoms of adjacent molecules (distance 2.669(3) Å) giving rise to chains along the b axis (Figure 6). Each chain is placed antiparallel to the following one in order to minimize the steric hindrance of the groups out of plane. The two chains interact by π–π overlapping between their aromatic rings, with a shortest distance of 3.35(1) Å. The so formed double chains are isolated because of the above-mentioned steric reasons.
![[1860-5397-9-253-6]](/bjoc/content/figures/1860-5397-9-253-6.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: Packing of 2 showing the F–F contacts along the chain (orange) and the π–π interactions that form the double chain (violet).
Figure 6: Packing of 2 showing the F–F contacts along the chain (orange) and the π–π interactions that form t...
We compared the geometries of compounds 3 (TUPSAZ) [8,10] and 5 (EFARUA) [8-10] (Figure 2) with those determined in the present work, 1 and 2. To describe the folding of the seven-membered ring we used the distance d in Å between the methylene carbon and the plane defined by the benzene ring. These values are 1.36 Å (3), 1.26 Å (5), 1.33 Å (1) and 1.57 Å (2), thus the 1,5-benzodiazepinone with a 4-methyl ring, 3, is more bent than that with a 4-phenyl ring, 5. More significant for the present work, the N-methyl substituent folded considerably the ring, compare 2 with 1, this being related to the inversion process discussed below.
Energies and tautomerism
For the 1H-derivatives five possible tautomers exist while for the N-methyl ones only three different tautomers are possible (Figure 7).
Figure 7: The different tautomers in the 1H and 1-methyl series.
Figure 7: The different tautomers in the 1H and 1-methyl series.
Mannschreck et al. already concluded in 1967 that 3 has the structure 3a based on a methylene signal at 3.14 ppm [11]. This is also compatible with tautomer 3d but considering that amides never exist as imidic acids, Mannschreck's conclusion is certainly right. Varma et al. reported in 2008 that the reaction between o-phenylenediamine and methyl acetylacetate yields the methoxy derivative 7 (Figure 8) without any reported proof [12]. In a subsequent paper they reported that the reaction of o-phenylenediamine using ethyl acetylacetate instead of methyl acetylacetate yielded the expected diazepinone that they represent using the tautomer 3d again without any reported proof, neither in the main text nor in the supplementary data [13].
Figure 8: 2-Methoxy-4-methyl-3H-1,5-benzodiazepine (7).
Figure 8: 2-Methoxy-4-methyl-3H-1,5-benzodiazepine (7).
A comprehensive theoretical study of the tautomerism of 3 was carried out by Okovytyy et al. in 2010, including monoethanol and diethanol solvates as well as dimeric forms [14] (they do not consider tautomer 3e). In the gas phase their relative energies (in kJ mol−1) are: 3a (0.0) > 3b (14.6) > 3d (48.5) > 3c (93.4) and with an ethanol molecule they are: 3a (0.0) > 3b (0.6) > 3d (51.3) > 3c (70.0). The great stabilization of 3b due to ethanol does not correspond to that observed by Mannschreck in CDCl3 [11]. Our calculations (gas phase) are reported in Table 1.
Our results agree with those of Okovytyy et al. [14] now including 3e: 3a (0.0) > 3b (14.7) > 3d (48.6) > 3e (64.0) > 3c (96.5). For the remaining compounds always is a (0.0) > b (18 kJ mol−1 in average), the other tautomers having considerably higher energies. Always tautomer b is destabilized by N-methylation (in average, 8.4 kJ mol−1) probably due to a steric effect; the conjugated tautomer b tends to be planar and this is indeed the case for 1H-derivatives 1b, 3b and 4b. The introduction of an N-methyl group, derivatives 2b, 4b and 6b, fold the seven-membered ring with a concomitant destabilization of these tautomers.
The tautomerism between a and b implies the breaking/formation of a C–H bond. This is similar to the case of acetylacetone (diketo and ketoenol tautomers) that when both tautomers are present, both can be observed by NMR because the tautomerization barrier is high enough. Therefore, if a CH2 group is observed in 1H or in 13C NMR in the case of 1,5-benzodiazepinones only tautomer a is present in solution.
Chemical shifts and spin–spin coupling constants (SSCC)
Mannschreck et al. reported the 1H NMR chemical shifts (δ in ppm) of 3a in CDCl3: 2.38 (CH3), 3.14 (CH2) and 9.99 (NH) [11]. Benasi et al. reported those of 5a (δA = 3.08, δB = 4.25, JAB = 12.00 Hz) and 6a (δA = 3.02, δB = 4.15, JAB = 12.00 Hz; CH3, 3.34) in acetone [15]. Those of 5a in DMSO-d6 are 3.87 and 4.62 ppm [16]. A paper by Bernardini et al. reports all the 13C NMR chemical shifts and some 1H–13C coupling constants for compounds 3–6 [17].
We report in Table 2 (1H and 19F NMR data) and Table 3 (13C and 15N NMR data) the results we have obtained for compounds 1 and 2 in different solvents and in the solid state together with the theoretical calculated values.
Table 2: 1H and 19F chemical shifts (δ, ppm, Δδ = δeq − δax) and SSCC (1H–1H; 1H–19F; 19F–19F Hz) of compounds 1 and 2 at 300 K together with the calculated values in ppm and Hz.
| Comp. | Conditions | CH3 | CH2 | NR | F6 | F7 | F8 | F9 |
|---|---|---|---|---|---|---|---|---|
| 1 | CDCl3 | 2.46 |
3.24
Δδ = 0.00 |
R = H
8.08 |
−147.8
3JF7 = 21.6 5JF9 = 9.6 |
−161.9
3JF8 = 21.6 |
−159.7
3JF9 = 21.6 |
−154.5 |
| 1 | toluene-d8 | 1.83 |
2.39
Δδ = 0.00 |
R = H
7.80 |
−148.5
3JF7 = 21.7 5JF9 = 9.6 |
−163.8
3JF8 = 21.7 |
−161.7
3JF9 = 21.7 |
−154.8 |
| 1 | DMSO-d6 | 2.32 |
3.24
Δδ = 0.00 |
R = H
10.66 |
−149.8
3JF7 = 22.7 5JF9 = 7.5 |
−164.6
3JF8 = 22.7 |
−162.5
3JF9 = 22.7 |
−151.1 |
| 1 | solid statea | – | – | – | −144.9 | −161.5 | −159.0 | −150.6 |
| 1 | calculated | 2.31 |
2.49 (ax)
3.23 (eq) Δδ = 0.74 Jae = −10.6b |
R = H
6.71 |
−142.8
3JF7 = −22.0 4JF8 = −1.5 5JF9 = +11.6 |
−163.0
3JF8 = −21.9 4JF9 = −6.0 |
−160.0
3JF9 = −22.0 |
−159.0
4JF7 = −6.0 |
| 2 | CDCl3 | 2.43 |
2.93 (ax)
3.53 (eq) Δδ = 0.60 Jae = 11.7 |
R = Me 3.30 (d)
5JF9 = 4.2 |
−148.5
3JF7 = 20.7 5JF9 = 8.8 |
−159.7
3JF8 = 20.7 |
−159.8
3JF9 = 20.7 |
−145.2b |
| 2 | toluene-d8 | 1.85 |
2.03 (ax)
2.86 (eq) Δδ = 0.83 Jae = 11.6 |
R = Me 2.88 (d)
5JF9 = 4.4 |
−148.7
3JF7 = 21.4 5JF9 = 8.4 |
−161.3
3JF8 = 21.4 |
−161.6
3JF9 = 21.4 |
−146.3
4JF7 = 8.4 5JCH3 = 4.4 |
| 2 | DMSO-d6 | 2.31 |
3.19 (ax)
3.45 (eq) Δδ = 0.27 Jae = 12.1 |
R = Me 3.18 (d)
5JF9 = 4.6 |
−150.0c | −162.1c | −162.1c | −144.7c |
| 2 | solid statea | – | – | – | −146.0 | −156.8 | −160.9 | −142.1 |
| 2 | calculated | 2.27 |
2.47 (ax)
3.20 (eq) Δδ = 0.73 Jae = −10.3 |
R = Me 3.13 (d)
5JF9 = 6.6 |
−144.3
3JF7 = −22.2 4JF8 = −2.8 5JF9 = +10.6 |
−160.4
3JF8 = −22.1 4JF9 = −3.3 |
−160.7
3JF = −21.6 |
−146.1
4JF7 = −3.3 |
aObtained using the hpdec.av sequence; bThis coupling constant agrees with the experimental one found at 193 K in toluene-d8 (see Barriers section); cComplex multiplet.
There are several interesting results concerning the data reported in Table 2. One of them is the JHF coupling constant present in the N-methyl group of compound 2. This coupling constant, of about 4.5 Hz, identifies unambiguously F9, i.e. it is a 5JHF9 because all the calculated values for the coupling constants between the N-methyl protons and the fluorine atoms are very small (about 0.1 Hz) except that with F9 (calculated 6.6 Hz). In the literature (Figure 9), there is a related coupling constant present in 2-fluoroacetophenone (8) [18]. Note that this 1H–19F coupling can be through-bonds, i.e. a 5J or through-space, a common problem involving 19F [19,20]. Starting from the F9 assignment, the (19F–19F) COSY experiments permitted to establish the correlation F9–F8–F7–F6, in both compounds.
Figure 9: 1H–19F coupling constant values either through-bond or through-space.
Figure 9: 1H–19F coupling constant values either through-bond or through-space.
Another interesting coupling is the geminal 2JHH ≈ 12 Hz of the methylene group in the case of compound 2. This coupling is well reproduced by the calculations ≈ −10.5 Hz. Next, we compared the experimental and calculated chemical shifts (Table 2). For 1H and 19F all together, (n = 44 values in solution) the correlations are very good (R2 = 1.000) but this is due to the fact that these nuclei appear at very different chemical shifts. Considering only the protons and not including the NH protons (n = 20), the regressions are good, for instance, δCDCl3 = −(0.4 ± 0.1) + (1.26 ± 0.04) δCalcd R2 = 0.995.
The part concerning 19F chemical shifts is less satisfactory. There are 32 values including those determined in the solid state. Imposing the intercept to be 0 (and considering that the calculations do not reproduce well the chemical shifts of F6 and F9, we found δ19F = (1.005 ± 0.003) δCalcd − (4.4 ± 0.7) F6 + (4.0 ± 0.7) F9 + (2.7 ± 0.7) CPMAS. The worse points are 1 DMSO-d6, F9 exp. −151.1, fitted −155.8; 2 toluene-d8, F9 exp. −146.3, fitted −142.9. The reason of this anomaly concerning the fluorine atoms closer to the nitrogen atoms remains unclear.
In what concerns the FF coupling constants, 3JFF and 5JFF agree with the calculated values; the average values being: experimental |21.4| (3JF) and |9.1| (3JF9) and calculated −22.0 (3JF) and 11.1 Hz (3JF9).
Table 3 reports the 13C and 15N NMR data; here the situation is more difficult because the 13C NMR signals of the benzene ring carbons are coupled with all the fluorine atoms giving rise to multiplets, which have been analyzed using the Mnova 8.1.0 NMR software [21] for spin simulation, and when needed by irradiation of the 1H nuclei to simplify the spectra. In the gs-HMBC (1H–13C) spectra, a correlation between the C4–CH3 protons and C4 permitted to assign to the latter the chemical shifts at 168.7 ppm for 1 and 170.9 for 2, in accordance with the calculated values. However, the 13C CPMAS signals corresponding to carbon atoms C6 to C9 could not be properly analyzed, and only the centers of the multiplets are given (138.1 and 138.6 ppm for 1 and 2, respectively). Some couplings involving the fluorine atoms are not well reproduced by the calculations, this is particularly apparent for the 1JCF, that are overestimated, in absolute value, by about 68 Hz. The overestimation and difficulty to calculate coupling constants involving 19F has been reported several times [20,22,23].
Table 3: 13C and 15N NMR chemical shifts (δ, ppm) and some coupling constants (Hz) of compounds 1 and 2 in solution and in the solid state together with the calculated values (ppm and Hz).
| Comp. | Conditions | C2 | C3 | C4 | 4-CH3 | N-CH3 | C5a | C9a |
|---|---|---|---|---|---|---|---|---|
| 1 | DMSO-d6 | 165.3 | 44.6 | 168.7 | 27.6 | – | 126.6 2J = 9.9 |
117.1
2J = 13.1 |
| 1 | CPMAS | 167.1 | 44.4 | 169.2 | 25.6 | – | 125.2 | 116.5 |
| 1 | Calcd | 161.4 | 44.5 | 165.8 | 27.9 | – |
126.5
2JF6 = 4.0 |
116.2
2JF9 = 3.4 |
| 2 | DMSO-d6 | 165.0 | 43.7 | 170.9 | 27.4 |
35.8
4JF9 = 8.7 |
128.4
2J = 11.2 |
121.2
2J = 8.9 |
| 2 | CPMAS | 165.8 | 42.6 | 173.3 | 27.3 | 36.2 | 128.7 | 121.5 |
| 2 | Calcd | 162.3 | 44.1 | 168.9 | 27.4 |
36.9
4JF9 = 8.5 |
129.8
2JF6 = 2.7 |
122.2
2JF9 = 2.1 |
| C6 | C7 | C8 | C9 | N1 | N5 | |||
| 1 | DMSO-d6 |
140.9
1J = 246.0 2J = 10.5 3J = 3.7 |
136.3
1J = 245.3 2J ≈ 13.5 2J ≈ 11.6 3J = 3.8 |
137.3
1J = 246.0 2J ≈ 14.0 2J ≈ 13.2 3J = 4.4 |
138.2
1J = 245.3 2J = 11.8 3J = 3.8 |
−254.3 | −86.9 | |
| 1 | CPMAS | 138.1a | 138.1a | 138.1a | 138.1a | –249.6 | −85.0 | |
| 1 | Calcd |
145.2
1J = −316.6 |
139.8
1J = −314.4 |
140.7
1J = −316.7 |
139.1
1J = −303.3 |
−256.7
3JN1F9 = −1.9 |
−82.0
4JN5F7 = 1.5 3JN5F6 = 5.2 |
|
| 2 | DMSO-d6 |
140.6
1J = 251.4 2J = 12.1 3J = 5.0 |
137.3
1J = 248.3 2J ≈ 16.2 2J ≈ 15.4 3J = 4.8 |
137.3 |
140.2
1J = 241.8 2J = 14.6 3J = 4.9 |
−264.3 | −90.5 | |
| 2 | CPMAS | 138.6a | 138.6a | 138.6a | 138.6a | −259.2 | −90.2 | |
| 2 | Calcd |
143.8
1J = −316.1 |
140.7
1J = −315.5 |
140.3
1J = −315.3 |
142.8
1J = −310.3 |
−256.2
3JN1F9 = −2.1 |
−85.0
4JN5F7 = 1.4 3JN5F6 = 5.2 |
|
aVery complex multiplet.
Concerning the 15N experimental spectra all nitrogen atoms appear as singlets in solution as well as in the solid state, only small coupling constants with the fluorine substituents have been theoretically calculated so most probably the width of the experimental signals mask them.
In Table S1 in Supporting Information File 1 the experimental (from references [11,15-17]) and calculated 1H, 13C and 15N NMR chemical shifts (δ, ppm) of compounds 3a to 6a are reported. The agreement between experimental and calculated values is either good or excellent.
Barriers (all in kJ mol−1)
The experimental inversion barriers of 3a, 5a (twice) and 6a have been determined and are given in Table 4. We have calculated those of 1a and 2a. The barriers for an AB system that become an A2 one depend on three values: i) the coalescence temperature TC; ii) the difference in Hz of the protons of the AB system (ΔνAB), and iii) the geminal coupling constant, JAB (or Jae). The inversion rate at the coalescence temperature for an AB system is given by kC = π/√2·√Δν2 + 6 JAB2 [11] and the barrier by the modified Eyring equation [24-26], ΔG‡ = 19.12·TC (10.32 + log TC/kC) [18-20]. From the values in Table 4 we have determined the corresponding experimental inversion barriers.
Table 4: Experimental al calculated inversion barriers (kJ mol–1).
| 1a | 2a | 3a | 4a | 5a | 6a | |
|---|---|---|---|---|---|---|
| ΔG‡exp. |
toluene-d8
TC = 230 K ΔνAB = 450.0 Hz JAB = 10.9 Hz 42.6 |
DMSO-d6
TC = 373 K ΔνAB = 103.5 Hz JAB = 12.1 Hz 75.0 toluene-d8 TC = 363 K ΔνAB = 303.1 Hz JAB = 11.6 Hz 69.8 |
pyridine-d5/CDCl3
39.8 [11] |
– |
acetone-d6
41.8 [15] 52.7 [16] |
acetone-d6
65.3 [15] |
| ΔG‡calcd. | 36.7 | 81.7 | 42.4 | 61.9 | 38.2 | 63.8 |
The agreement between experimental and calculated values is satisfactory: using for 2a the 75.0 kJ mol−1 and for 5a the 41.8 kJ mol−1 values we obtained by linear regression (no intercept) ΔG‡exp. = (0.99 ± 0.04) ΔG‡calcd, n = 5, R2 = 0.993. This equation predicts for 4a 61.0 kJ mol−1. Note the increase between toluene and DMSO that corresponds to the raise of inversion barriers with that of the solvent polarity; a similar behavior has been reported for diazepam (7-chloro-1,3-dihydro-1-methyl-5-phenyl-2H-1,4-benzodiazepin-2-one) [27].
When using calculated values it is possible to analyze the main effects on the barriers that in the present case are three: i) N-methylation; ii) 6,7,8,9-tetrafluorination; iii) the substituent at position 4 (CH3 or C6H5). This last effect is negligible, the other two interact, then a product term (i · ii) is necessary to model the behavior. The regression corresponds to the following equation (all values in kJ mol−1):
Calculated barrier = (40.3 ± 1.6) + (22.6 ± 2.3) NMe − (3.6 ± 2.8) C6F4 + (22.5 ± 4.0) NMe*C6F4, n = 6, R2 = 0.993
The average barrier is 40.3 kJ mol−1. N-Methylation increases the barrier 22.6 kJ mol−1 in average; the introduction of four F atoms produces a small effect of 3.6 kJ mol−1 but when there is simultaneously an N-methyl group and four F atoms (compound 2a), the increase of the barrier is considerable (22.5 kJ mol−1). An examination of the TS for 2a shows that the protons of the N-methyl group are very close to F9 (Figure 10).
![[1860-5397-9-253-10]](/bjoc/content/figures/1860-5397-9-253-10.png?scale=1.5&max-width=1024&background=FFFFFF)
Figure 10: The optimized geometry of the TS of 2a inversion.
Figure 10: The optimized geometry of the TS of 2a inversion.
Conclusion
A clearer picture of the behavior of 1,5-benzodiazepinones emerges from the present paper. Concerning tautomerism, our results confirm previous studies while extending them to the 6,7,8,9-tetrafluoro derivatives. The folding of the structures in the solid-state is general, the N-methyl group having a marked effect. An exhaustive NMR study of the tetrafluoro derivatives, together with literature data on four other non-fluorinated 1,5-benzodiazepinones, lead to values of the chemical shifts that compare well with GIAO calculated ones with the exception of F6 and F9. Finally, the inversion barrier of the seven-membered ring of the new compounds has been determined and compared with theoretically calculated values, illustrating the considerable effect of the N-methylation particularly when there is a fluorine atom on C9.
Experimental
General Information. All chemicals cited in the synthetic procedures are commercial compounds. Melting points were determined by DSC with a SEIKO DSC220C connected to a model SSC5200H disk station. Thermograms (sample size 0.004 g) were recorded with a scan rate of 5.0 °C. Column chromatography was performed on silica gel (Merck 60, 70–230 mesh) and elemental analyses using a Perkin-Elmer 240 apparatus.
6,7,8,9-Tetrafluoro-4-methyl-1,3-dihydro-2H-1,5-benzodiazepin-2-one (1). 1,2-Diamino-3,4,5,6-tetrafluorobenzene (0.50 g, 2.78 mmol) and ethyl acetylacetate (0.36 mL, 2.85 mmol) were heated at 120 °C in anhydrous xylene (5 mL) for 6 hours. The mixture was cooled and then a solid precipitated. This residue was washed with diethyl ether to give compound 1 (0.43 g, 63%); white solid; mp 155.2 °C. Anal. calcd for C10H6F4N2O: C, 48.79; H, 2.46; N, 11.38; found: C, 48.04; H, 2.60; N, 11.41.
6,7,8,9-Tetrafluoro-1,4-dimethyl-1,3-dihydro-2H-1,5-benzodiazepin-2-one (2). A solution of 1 (0.40 g, 1.62 mmol) in DMF (2 mL) was heated at 110 °C in the presence of iodomethane (0.11 mL, 1.79 mmol), K2CO3 (0.27 g, 1.95 mmol) and a catalytic quantity of KI for 90 min. The mixture was cooled, treated with cold water and extracted with ethyl acetate. The ethyl acetate was evaporated and the crude was purified by column chromatography (hexane/ethyl acetate 7:3) to afford compound 2 (0.34 g, 80%); pale yellow solid; mp 132.2 °C. Anal. calcd for C11H8F4N2O: C, 50.78; H, 3.10; N, 10.77; found: C, 50.91; H, 3.15; N, 10.76.
X-ray data collection and structure refinement. Data collection for all compounds was carried out at room temperature on a Bruker Smart CCD diffractometer using graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) operating at 50 kV and 30 mA for 1 and 2. In all cases, data were collected over a hemisphere of the reciprocal space by combination of three exposure sets. Each exposure was of 20 s covered 0.3 in ω. The cell parameter were determined and refined by a least-squares fit of all reflections. The first 100 frames were recollected at the end of the data collection to monitor crystal decay, and no appreciable decay was observed. A summary of the fundamental crystal and refinement data is given in Table 5.
Table 5: Crystal data and refinement data for 1 and 2.
| Crystal Data | 1 | 2 |
|---|---|---|
| Empirical formula | C10H6 F4N 2O1 | C11H8 F4N2O1 |
| Formula wt | 246.17 | 260.19 |
| Crystal system. Space group | Monoclinic P21/c | Triclinic P–1 |
| a/Å | 5.2821(5) | 7.224(4) |
| b/Å | 18.255(1) | 8.064(4) |
| c/Å | 10.2102(9) | 10.478(5) |
| α/° | 77.136(9) | |
| β/° | 100.93(1) | 76.311(9) |
| γ/° | 68.510(8) | |
| V/Å3 | 966.6(1) | 545.5(5) |
| Z | 4 | 2 |
| Dc /g/cm3 | 1.692 | 1.584 |
| µ(Mo Kα) /mm–1 | 0.164 | 0.150 |
| F(000) | 496 | 264 |
| θ range/° | 2.23 to 25.01 | 2.02 to 25.00 |
| Index ranges | −6, −18, −8 to 6, 21, 12 | −8, −9, −12 to 7, 9, 12 |
| Reflections collected | 4110 | 4184 |
| Unique reflections [Rint] | 1709 [Rint = 0.0233] | 1869 [R(int) = 0.0350] |
| Completeness to theta | 100% | 97.0% |
| Data/restraints/params | 1709/0/155 | 1869/0/163 |
| Goodness-of-fit on F2 | 1.006 | 0.999 |
| R1 (reflns obsd) [I > 2σ(I)] a | 0.0386 (1267) | 0.0443 (1306) |
| wR2 (all data) b | 0.0935 | 0.1539 |
aR1 = Σ||Fo|− |Fc||/Σ|Fo|. bwR2 = {Σ[w(Fo2 − Fc2)2]/Σ[w(Fo2)2]}.
The structures were solved by direct methods and refined by full-matrix least-square procedures on F2 (SHELXL-97) [28]. All non-hydrogen atoms were refined anisotropically.
The hydrogen atoms were included in their calculated positions and refined riding on the respective carbon atoms with the exception of hydrogen H1 bonded to N1 for 1 that was located in a Fourier synthesis and refined riding on the respective bonded atom.
Further crystallographic details for the structure reported in this paper may be obtained from The Cambridge Crystallographic Data Center, on quoting the depository numbers CCDC 946878 and 946879. Copies of the data can be obtained free of charge on application to The Director, CCDC, 12 Union Road, Cambridge DB2 1EZ, UK (Fax: int. code +(1223)336-033; email: deposit@ccdc.cam.ac.uk).
Theoretical calculations. The geometry of the molecules has been fully optimized with the hybrid HF/DFT B3LYP [29-31] computational method and the 6-31G(d) basis set [32]. Frequency calculations have been carried out at the same computational level to verify that the structures obtained correspond to energetic minima. A further optimization has been carried out at the B3LYP/6-311++G(d,p) level [33,34]. These geometries have been used for the calculations of the absolute chemical shieldings with the GIAO method [35,36] and the B3LYP/6-311++G(d,p) computational level. All the calculations have been carried out with the Gaussian-09 package [37].
The literature equations shown in Figure 11 have been used to transform absolute shieldings into chemical shifts.
Figure 11: Equations used to transform absolute shieldings into chemical shifts [38,39].
Figure 11: Equations used to transform absolute shieldings into chemical shifts [38,39].
Experimental NMR
Solution spectra were recorded on a Bruker DRX 400 (9.4 Tesla, 400.13 MHz for 1H, 100.62 MHz for 13C, 40.56 MHz for 15N and 379.50 MHz for 19F) using a 5 mm QNP direct-detection probehead equipped with a z-gradient coil, at 300 K. Chemical shifts (δ in ppm) are given from internal solvent, DMSO-d6 2.49 for 1H and 39.5 for 13C; CDCl3 7.26 for 1H and toluene-d8 2.09 for 1H, and for 15N and 19F NMR, nitromethane (0.00) and one drop of CFCl3 in CDCl3 (0.00) were used as external references.
Typical parameters for 1H NMR spectra were spectral width of 4800 Hz and pulse width of 10.25 μs at an attenuation level of –3.0 dB. Typical parameters for 13C NMR spectra were spectral width of 21 kHz, pulse width of 8.75 μs at an attenuation level of –3 dB and relaxation delay of 2 s, WALTZ-16 used for broadband proton decoupling; the FIDS were multiplied by an exponential weighting (lb = 1 Hz) before Fourier transformation. Typical parameters for 19F NMR spectra were spectral width of 55 kHz, pulse width of 13.75 μs at an attenuation level of –6 dB and relaxation delay of 1 s. WALTZ-16 was used for broadband proton decoupling 19F{1H}, the FIDS were multiplied by an exponential weighting (lb = 1 Hz) before Fourier transformation. Homonuclear 19F−19F experiment does not require any modification of the standard gs-COSY pulse sequences; selected parameters for 19F COSY spectra were: spectral width of 55 KHz, TD1 = 512 for F1 domain, spectral width of 55 KHz, TD1 = 1024 for F2 domain, number of scans 4, dummy scans DS = 2 and relaxation delay of 1 s.
Inverse proton detected heteronuclear shift correlation spectra, (1H–13C) gs-HMBC, were acquired and processed using standard Bruker NMR software and in nonphase-sensitive mode. Gradient selection was achieved through a 5% sine truncated shaped pulse gradient of 1 ms.
Inverse proton-detected heteronuclear shift correlation spectra, (1H–15N) gs-HMQC and (1H–15N) gs-HMBC, were acquired and processed using standard Bruker NMR software and in nonphase-sensitive mode. Gradient selection was achieved through a 5% sine truncated shaped pulse gradient of 1 ms. Selected parameters for (1H–15N) gs-HMQC and (1H–15N) gs-HMBC spectra were spectral width of 3500 Hz for 1H and 12.5 kHz for 15N, 1024 x 256 data set, number of scans 4, relaxation delay of 1 s, 37–60 ms delay for evolution of the 15N–1H long-range coupling. The FIDs were processed using zero filling in the F1 domain and a sine-bell window function in both dimensions was applied prior to Fourier transformation.
Variable temperature was performed using a Bruker BVT3000 temperature unit to control the temperature of the cooling gas stream and an exchanger to achieve low temperatures. To avoid problems at low temperatures caused by air moisture, pure nitrogen was used as bearing, driving and cooling gas.
Solid state 13C (100.73 MHz) and 15N (40.60 MHz) CPMAS NMR spectra have been obtained on a Bruker WB 400 spectrometer at 300 K using a 4 mm DVT probehead. Samples were carefully packed in 4 mm diameter cylindrical zirconia rotors with Kel-F end-caps. Operating conditions involved 2.9 µs 90° 1H pulses and decoupling field strength of 86.2 kHz by TPPM sequence. 13C NMR spectra were originally referenced to a glycine sample and then the chemical shifts were recalculated to the Me4Si (for the carbonyl atom δ (glycine) = 176.1 ppm) and 15N NMR spectra to 15NH4Cl and then converted to nitromethane scale using the relationship: δ 15N(nitromethane) = δ 15N(ammonium chloride) − 338.1 ppm.
The typical acquisition parameters for 13C CPMAS were: spectral width, 40 kHz; recycle delay, 5 s; acquisition time, 30 ms; contact time, 2 ms; and spin rate, 12 kHz. In order to distinguish protonated and unprotonated carbon atoms, the NQS (non-quaternary suppression) experiment by conventional cross-polarization was recorded; before the acquisition the decoupler is switched off for a very short time of 25 μs [40-42]. And for 15N CPMAS were: spectral width, 40 kHz; recycle delay, 5 s; acquisition time, 35 ms; contact time, 6 ms; and spin rate, 6 kHz.
Solid-state 19F (376.94 MHz) NMR spectra have been obtained on a Bruker WB 400 spectrometer using a MAS DVT BL2.5 X/F/H trible resonance probehead. Samples were carefully packed in 2.5 mm diameter cylindrical zirconia rotors with Kel-F end-caps. Samples were spun at the magic angle at rates of 25 kHz and the experiments were carried out at ambient probe temperature.
Typical parameters for single pulse 19F MAS NMR spectra were: spectral width, 75 KHz; pulse width, 2.5 μs; recycle delay, 10 s; scans, 128; and spin rate, 25 kHz.
The typical acquisition parameters 19F{1H} MAS were: spectral width, 75 kHz; recycle delay, 10 s; pulse width, 2.5 μs and proton decoupling field strength of 100 kHz by SPINAL-64 sequence; recycle delay, 10 s; acquisition time, 25 ms; 128 scans; and spin rate, 25 kHz.
The 19F spectra were referenced to ammonium trifluoroacetate sample and then the chemical shifts were recalculated to the CFCl3 [δ (CF3COONH4+)] = –72.0 ppm)
Supporting Information
Variable temperature 1H NMR spectra, 13C, 15N, 19F solid state NMR spectra; Table S1 containing calculated and some experimental 1H, 13C and 15N chemical shifts (δ, ppm) of compounds 3a to 6a; Geometry (Å), energy (hartree) and number of imaginary frequencies of the different tautomers calculated at the B3LYP/6-311++G(d,p) computational level.
| Supporting Information File 1: Additional material. | ||
| Format: PDF | Size: 995.2 KB | Download |
References
-
Claramunt, R. M.; Alkorta, I.; Elguero, J. Comput. Theor. Chem. 2013, 1019, 108–115. doi:10.1016/j.comptc.2013.07.002
Return to citation in text: [1] -
Hamor, T. A.; Martin, I. L. The Benzodiazepines. In Progress in Medicinal Chemistry; Ellis, G. P.; West, G. B., Eds.; Elsevier: Amsterdam, 1983; Vol. 20. doi:10.1016/S0079-6468(08)70219-4
Return to citation in text: [1] -
Müller, W. E. The Benzodiazepine Receptor: Drug Acceptor only for a Physiologically Relevant Part of our Central Nervous System; Cambridge University Press: Cambridge, UK, 1987.
Return to citation in text: [1] -
Squires, R. F., Ed. GABA and benzodiazepine receptors; CRC Press: Boca Raton, Florida, USA, 1987; Vol. I, II.
Return to citation in text: [1] -
Trimble, M.; Hindmarch, I., Eds. Benzodiazepines; Wrightson Biomedical Publishing Ltd.: Petersfield, UK, 2000.
Return to citation in text: [1] -
Berna, M. J.; Jensen, R. T. Curr. Top. Med. Chem. 2007, 7, 1211–1231. doi:10.2174/156802607780960519
Return to citation in text: [1] -
Saber, A.; Zouihri, H.; Essassi, E. M.; Ng, S. W. Acta Crystallogr., Sect. E: Struct. Rep. Online 2010, 66, o1408. doi:10.1107/S1600536810017885
Return to citation in text: [1] -
Allen, F. H. Acta Crystallogr., Sect. B 2002, 58, 380–388. doi:10.1107/S0108768102003890
Return to citation in text: [1] [2] [3] -
Allen, F. H.; Motherwell, W. D. S. Acta Crystallogr., Sect. B 2002, 58, 407–422. doi:10.1107/S0108768102004895
Return to citation in text: [1] [2] -
Akkurt, M.; Kennedy, A. R.; Younes, S. H. H.; Mohamed, S. K.; Abdelhamid, A. A. Acta Crystallogr., Sect. E: Struct. Rep. Online 2012, 68, o3356. doi:10.1107/S160053681204651X
Return to citation in text: [1] [2] -
Mannschreck, A.; Rissmann, G.; Vögtle, F.; Wild, D. Chem. Ber. 1967, 100, 335–346. doi:10.1002/cber.19671000138
Return to citation in text: [1] [2] [3] [4] [5] [6] -
Polshettiwar, V.; Varma, R. S. Tetrahedron Lett. 2008, 49, 397–400. doi:10.1016/j.tetlet.2007.11.017
Return to citation in text: [1] -
Vaddula, B. R.; Varma, R. S.; Leazer, J. Tetrahedron Lett. 2013, 54, 1538–1541. doi:10.1016/j.tetlet.2013.01.029
Return to citation in text: [1] -
Okovytyy, S. I.; Sviatenko, L. K.; Gaponov, A. A.; Kasyan, L. I.; Tarabara, I. N.; Leszczynski, J. Eur. J. Org. Chem. 2010, 280–291. doi:10.1002/ejoc.200900689
Return to citation in text: [1] [2] -
Benasi, R.; Lazzeretti, P.; Taddei, F.; Nardi, D.; Tajana, A. Org. Magn. Reson. 1976, 8, 387–388. doi:10.1002/mrc.1270080715
Return to citation in text: [1] [2] [3] [4] -
Chidichimo, G.; Longeri, M.; Menniti, G.; Romeo, G.; Ferlazzo, A. Org. Magn. Reson. 1984, 22, 52–54. doi:10.1002/mrc.1270220111
Return to citation in text: [1] [2] [3] -
Bernardini, A.; Viallefont, P.; Essassi, E. M.; Zniber, R. Org. Magn. Reson. 1982, 18, 134–137. doi:10.1002/mrc.1270180304
Return to citation in text: [1] [2] -
Berger, S.; Braun, S.; Kalinowski, H.-O. NMR Spectroscopy of the Non-Metallic Elements; John Wiley & Sons: Chichester, UK, 1997; p 617.
Return to citation in text: [1] [2] -
Mallory, F. B.; Mallory, C. W. J. Am. Chem. Soc. 1985, 107, 4816–4819. doi:10.1021/ja00303a002
Return to citation in text: [1] [2] -
Alkorta, I.; Elguero, J. Int. J. Mol. Sci. 2003, 4, 64–92. doi:10.3390/i4030064
Return to citation in text: [1] [2] [3] -
MNova program by Mestrelab Research (http://www.mestrec.com) running under Windows XP.
Return to citation in text: [1] -
Pecul, M.; Sadlej, J.; Leszczynski, J. J. Chem. Phys. 2001, 115, 5498–5506. doi:10.1063/1.1398099
Return to citation in text: [1] -
Fonseca, T. A. O.; Ramalho, T. C.; Freitas, M. P. Magn. Reson. Chem. 2012, 50, 551–556. doi:10.1002/mrc.3837
Return to citation in text: [1] -
Sammes, M. P.; Ho, K.-W.; Katritzky, A. R. Magn. Reson. Chem. 1985, 23, 720–724. doi:10.1002/mrc.1260230908
Return to citation in text: [1] -
García-Frutos, E. M.; Gómez-Lor, B.; Monge, Á.; Gutiérrez-Puebla, E.; Alkorta, I.; Elguero, J. Chem.–Eur. J. 2008, 14, 8555–8561. doi:10.1002/chem.200800911
Return to citation in text: [1] -
Alkorta, I.; Elguero, J.; Roussel, C. Tetrahedron: Asymmetry 2011, 22, 1180–1183. doi:10.1016/j.tetasy.2011.06.010
Return to citation in text: [1] -
Paizs, B.; Simonyi, M. Chirality 1999, 11, 651–658. doi:10.1002/(SICI)1520-636X(1999)11:8<651::AID-CHIR7>3.0.CO;2-5
Return to citation in text: [1] -
‘SHELX97, Program for Refinement of Crystal Structure’; University of Göttingen: Göttingen, Germany, 1997.
Return to citation in text: [1] -
Becke, A. D. Phys. Rev. A 1988, 38, 3098–3100. doi:10.1103/PhysRevA.38.3098
Return to citation in text: [1] -
Becke, A. D. J. Chem. Phys. 1993, 98, 5648–5652. doi:10.1063/1.464913
Return to citation in text: [1] -
Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785–789. doi:10.1103/PhysRevB.37.785
Return to citation in text: [1] -
Hariharan, P. C.; Pople, J. A. Theor. Chim. Acta 1973, 28, 213–222. doi:10.1007/BF00533485
Return to citation in text: [1] -
Ditchfield, R.; Hehre, W. J.; Pople, J. A. J. Chem. Phys. 1971, 54, 724–728. doi:10.1063/1.1674902
Return to citation in text: [1] -
Frisch, M. J.; Pople, J. A.; Binkley, J. S. J. Chem. Phys. 1984, 80, 3265–3269. doi:10.1063/1.447079
Return to citation in text: [1] -
Ditchfield, R. Mol. Phys. 1974, 27, 789–807. doi:10.1080/00268977400100711
Return to citation in text: [1] -
London, F. J. Phys. Radium 1937, 8, 397–409. doi:10.1051/jphysrad:01937008010039700
Return to citation in text: [1] -
Gaussian 09, Revision A.1, Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, Jr., J. A.; Peralta, J. E.; Ogliaro, F.; Bearpark, M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V. N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, N. J.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, Ö.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J. Gaussian, Inc., Wallingford CT, 2009.
Return to citation in text: [1] -
Silva, A. M. S.; Sousa, R. M. S.; Jimeno, M. L.; Blanco, F.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2008, 46, 859–864. doi:10.1002/mrc.2272
Return to citation in text: [1] -
Blanco, F.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2007, 45, 797–800. doi:10.1002/mrc.2053
Return to citation in text: [1] -
DuBois Murphy, P. J. Magn. Reson. 1983, 52, 343–345. doi:10.1016/0022-2364(83)90209-3
Return to citation in text: [1] -
DuBois Murphy, P. J. Magn. Reson. 1985, 62, 303–308. doi:10.1016/0022-2364(85)90063-0
Return to citation in text: [1] -
Alemany, L. B.; Grant, D. M.; Alger, T. D.; Pugmire, R. J. J. Am. Chem. Soc. 1983, 105, 6697–6704. doi:10.1021/ja00360a025
Return to citation in text: [1]
| 15. | Benasi, R.; Lazzeretti, P.; Taddei, F.; Nardi, D.; Tajana, A. Org. Magn. Reson. 1976, 8, 387–388. doi:10.1002/mrc.1270080715 |
| 27. | Paizs, B.; Simonyi, M. Chirality 1999, 11, 651–658. doi:10.1002/(SICI)1520-636X(1999)11:8<651::AID-CHIR7>3.0.CO;2-5 |
| 28. | ‘SHELX97, Program for Refinement of Crystal Structure’; University of Göttingen: Göttingen, Germany, 1997. |
| 1. | Claramunt, R. M.; Alkorta, I.; Elguero, J. Comput. Theor. Chem. 2013, 1019, 108–115. doi:10.1016/j.comptc.2013.07.002 |
| 8. | Allen, F. H. Acta Crystallogr., Sect. B 2002, 58, 380–388. doi:10.1107/S0108768102003890 |
| 10. | Akkurt, M.; Kennedy, A. R.; Younes, S. H. H.; Mohamed, S. K.; Abdelhamid, A. A. Acta Crystallogr., Sect. E: Struct. Rep. Online 2012, 68, o3356. doi:10.1107/S160053681204651X |
| 16. | Chidichimo, G.; Longeri, M.; Menniti, G.; Romeo, G.; Ferlazzo, A. Org. Magn. Reson. 1984, 22, 52–54. doi:10.1002/mrc.1270220111 |
| 40. | DuBois Murphy, P. J. Magn. Reson. 1983, 52, 343–345. doi:10.1016/0022-2364(83)90209-3 |
| 41. | DuBois Murphy, P. J. Magn. Reson. 1985, 62, 303–308. doi:10.1016/0022-2364(85)90063-0 |
| 42. | Alemany, L. B.; Grant, D. M.; Alger, T. D.; Pugmire, R. J. J. Am. Chem. Soc. 1983, 105, 6697–6704. doi:10.1021/ja00360a025 |
| 8. | Allen, F. H. Acta Crystallogr., Sect. B 2002, 58, 380–388. doi:10.1107/S0108768102003890 |
| 9. | Allen, F. H.; Motherwell, W. D. S. Acta Crystallogr., Sect. B 2002, 58, 407–422. doi:10.1107/S0108768102004895 |
| 17. | Bernardini, A.; Viallefont, P.; Essassi, E. M.; Zniber, R. Org. Magn. Reson. 1982, 18, 134–137. doi:10.1002/mrc.1270180304 |
| 7. | Saber, A.; Zouihri, H.; Essassi, E. M.; Ng, S. W. Acta Crystallogr., Sect. E: Struct. Rep. Online 2010, 66, o1408. doi:10.1107/S1600536810017885 |
| 11. | Mannschreck, A.; Rissmann, G.; Vögtle, F.; Wild, D. Chem. Ber. 1967, 100, 335–346. doi:10.1002/cber.19671000138 |
| 37. | Gaussian 09, Revision A.1, Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, Jr., J. A.; Peralta, J. E.; Ogliaro, F.; Bearpark, M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V. N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, N. J.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, Ö.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J. Gaussian, Inc., Wallingford CT, 2009. |
| 2. | Hamor, T. A.; Martin, I. L. The Benzodiazepines. In Progress in Medicinal Chemistry; Ellis, G. P.; West, G. B., Eds.; Elsevier: Amsterdam, 1983; Vol. 20. doi:10.1016/S0079-6468(08)70219-4 |
| 3. | Müller, W. E. The Benzodiazepine Receptor: Drug Acceptor only for a Physiologically Relevant Part of our Central Nervous System; Cambridge University Press: Cambridge, UK, 1987. |
| 4. | Squires, R. F., Ed. GABA and benzodiazepine receptors; CRC Press: Boca Raton, Florida, USA, 1987; Vol. I, II. |
| 5. | Trimble, M.; Hindmarch, I., Eds. Benzodiazepines; Wrightson Biomedical Publishing Ltd.: Petersfield, UK, 2000. |
| 6. | Berna, M. J.; Jensen, R. T. Curr. Top. Med. Chem. 2007, 7, 1211–1231. doi:10.2174/156802607780960519 |
| 15. | Benasi, R.; Lazzeretti, P.; Taddei, F.; Nardi, D.; Tajana, A. Org. Magn. Reson. 1976, 8, 387–388. doi:10.1002/mrc.1270080715 |
| 38. | Silva, A. M. S.; Sousa, R. M. S.; Jimeno, M. L.; Blanco, F.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2008, 46, 859–864. doi:10.1002/mrc.2272 |
| 39. | Blanco, F.; Alkorta, I.; Elguero, J. Magn. Reson. Chem. 2007, 45, 797–800. doi:10.1002/mrc.2053 |
| 13. | Vaddula, B. R.; Varma, R. S.; Leazer, J. Tetrahedron Lett. 2013, 54, 1538–1541. doi:10.1016/j.tetlet.2013.01.029 |
| 11. | Mannschreck, A.; Rissmann, G.; Vögtle, F.; Wild, D. Chem. Ber. 1967, 100, 335–346. doi:10.1002/cber.19671000138 |
| 33. | Ditchfield, R.; Hehre, W. J.; Pople, J. A. J. Chem. Phys. 1971, 54, 724–728. doi:10.1063/1.1674902 |
| 34. | Frisch, M. J.; Pople, J. A.; Binkley, J. S. J. Chem. Phys. 1984, 80, 3265–3269. doi:10.1063/1.447079 |
| 12. | Polshettiwar, V.; Varma, R. S. Tetrahedron Lett. 2008, 49, 397–400. doi:10.1016/j.tetlet.2007.11.017 |
| 14. | Okovytyy, S. I.; Sviatenko, L. K.; Gaponov, A. A.; Kasyan, L. I.; Tarabara, I. N.; Leszczynski, J. Eur. J. Org. Chem. 2010, 280–291. doi:10.1002/ejoc.200900689 |
| 35. | Ditchfield, R. Mol. Phys. 1974, 27, 789–807. doi:10.1080/00268977400100711 |
| 36. | London, F. J. Phys. Radium 1937, 8, 397–409. doi:10.1051/jphysrad:01937008010039700 |
| 11. | Mannschreck, A.; Rissmann, G.; Vögtle, F.; Wild, D. Chem. Ber. 1967, 100, 335–346. doi:10.1002/cber.19671000138 |
| 29. | Becke, A. D. Phys. Rev. A 1988, 38, 3098–3100. doi:10.1103/PhysRevA.38.3098 |
| 30. | Becke, A. D. J. Chem. Phys. 1993, 98, 5648–5652. doi:10.1063/1.464913 |
| 31. | Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785–789. doi:10.1103/PhysRevB.37.785 |
| 8. | Allen, F. H. Acta Crystallogr., Sect. B 2002, 58, 380–388. doi:10.1107/S0108768102003890 |
| 9. | Allen, F. H.; Motherwell, W. D. S. Acta Crystallogr., Sect. B 2002, 58, 407–422. doi:10.1107/S0108768102004895 |
| 10. | Akkurt, M.; Kennedy, A. R.; Younes, S. H. H.; Mohamed, S. K.; Abdelhamid, A. A. Acta Crystallogr., Sect. E: Struct. Rep. Online 2012, 68, o3356. doi:10.1107/S160053681204651X |
| 14. | Okovytyy, S. I.; Sviatenko, L. K.; Gaponov, A. A.; Kasyan, L. I.; Tarabara, I. N.; Leszczynski, J. Eur. J. Org. Chem. 2010, 280–291. doi:10.1002/ejoc.200900689 |
| 32. | Hariharan, P. C.; Pople, J. A. Theor. Chim. Acta 1973, 28, 213–222. doi:10.1007/BF00533485 |
| 21. | MNova program by Mestrelab Research (http://www.mestrec.com) running under Windows XP. |
| 18. | Berger, S.; Braun, S.; Kalinowski, H.-O. NMR Spectroscopy of the Non-Metallic Elements; John Wiley & Sons: Chichester, UK, 1997; p 617. |
| 19. | Mallory, F. B.; Mallory, C. W. J. Am. Chem. Soc. 1985, 107, 4816–4819. doi:10.1021/ja00303a002 |
| 20. | Alkorta, I.; Elguero, J. Int. J. Mol. Sci. 2003, 4, 64–92. doi:10.3390/i4030064 |
| 15. | Benasi, R.; Lazzeretti, P.; Taddei, F.; Nardi, D.; Tajana, A. Org. Magn. Reson. 1976, 8, 387–388. doi:10.1002/mrc.1270080715 |
| 16. | Chidichimo, G.; Longeri, M.; Menniti, G.; Romeo, G.; Ferlazzo, A. Org. Magn. Reson. 1984, 22, 52–54. doi:10.1002/mrc.1270220111 |
| 18. | Berger, S.; Braun, S.; Kalinowski, H.-O. NMR Spectroscopy of the Non-Metallic Elements; John Wiley & Sons: Chichester, UK, 1997; p 617. |
| 19. | Mallory, F. B.; Mallory, C. W. J. Am. Chem. Soc. 1985, 107, 4816–4819. doi:10.1021/ja00303a002 |
| 20. | Alkorta, I.; Elguero, J. Int. J. Mol. Sci. 2003, 4, 64–92. doi:10.3390/i4030064 |
| 11. | Mannschreck, A.; Rissmann, G.; Vögtle, F.; Wild, D. Chem. Ber. 1967, 100, 335–346. doi:10.1002/cber.19671000138 |
| 11. | Mannschreck, A.; Rissmann, G.; Vögtle, F.; Wild, D. Chem. Ber. 1967, 100, 335–346. doi:10.1002/cber.19671000138 |
| 24. | Sammes, M. P.; Ho, K.-W.; Katritzky, A. R. Magn. Reson. Chem. 1985, 23, 720–724. doi:10.1002/mrc.1260230908 |
| 25. | García-Frutos, E. M.; Gómez-Lor, B.; Monge, Á.; Gutiérrez-Puebla, E.; Alkorta, I.; Elguero, J. Chem.–Eur. J. 2008, 14, 8555–8561. doi:10.1002/chem.200800911 |
| 26. | Alkorta, I.; Elguero, J.; Roussel, C. Tetrahedron: Asymmetry 2011, 22, 1180–1183. doi:10.1016/j.tetasy.2011.06.010 |
| 20. | Alkorta, I.; Elguero, J. Int. J. Mol. Sci. 2003, 4, 64–92. doi:10.3390/i4030064 |
| 22. | Pecul, M.; Sadlej, J.; Leszczynski, J. J. Chem. Phys. 2001, 115, 5498–5506. doi:10.1063/1.1398099 |
| 23. | Fonseca, T. A. O.; Ramalho, T. C.; Freitas, M. P. Magn. Reson. Chem. 2012, 50, 551–556. doi:10.1002/mrc.3837 |
| 11. | Mannschreck, A.; Rissmann, G.; Vögtle, F.; Wild, D. Chem. Ber. 1967, 100, 335–346. doi:10.1002/cber.19671000138 |
| 15. | Benasi, R.; Lazzeretti, P.; Taddei, F.; Nardi, D.; Tajana, A. Org. Magn. Reson. 1976, 8, 387–388. doi:10.1002/mrc.1270080715 |
| 16. | Chidichimo, G.; Longeri, M.; Menniti, G.; Romeo, G.; Ferlazzo, A. Org. Magn. Reson. 1984, 22, 52–54. doi:10.1002/mrc.1270220111 |
| 17. | Bernardini, A.; Viallefont, P.; Essassi, E. M.; Zniber, R. Org. Magn. Reson. 1982, 18, 134–137. doi:10.1002/mrc.1270180304 |
© 2013 Pérez-Torralba et al; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)