Abstract
The KP15 nanowires with one-dimensional properties has a defect-free surface, high anisotropy, and carrier mobility which is desirable for the development of novel nanodevices. However, the preparation of nanoscale KP15 is still inefficient. In this work, the Hansen solubility parameters of KP15 were first obtained. Based on the Hansen's empirical theory, the concentration of liquid-exfoliated KP15 nanowires was improved to 0.0458 mg·mL−1 by a solution containing 50% water and 50% acetone. Approximately 79% of the KP15 nanowires had a thickness value below 50 nm and 60.9% of them had a width value below 100 nm. The thinnest KP15 nanowires reached 5.1 nm and had smooth boundaries. Meanwhile, strong temperature-dependent Raman response in exfoliated KP15 nanowires has been observed, which indicates a strong phonon–phonon coupling in those nanowires. This is helpful for non-invasive temperature measurements of KP15 nanodevices.
Introduction
Low-dimensional materials have drawn significant attention in recent years. So far, not only new composite materials with excellent properties have been obtained by the synthesis of different materials, but also low-dimensional materials with different properties than those of bulk materials have been synthesized by physical and chemical methods. For instance, Bingjun Yang used one-dimensional graphene nanoscroll-wrapped MnO nanoparticles as anode materials to promote the rapid diffusion and electron transfer of lithium, and Rongjun Zhao prepared n-butanol gas sensors with one-dimensional In2O3 nanorods [1,2]. Different from 2D materials, 1D materials generally have a chain-like crystal structure and are easily exfoliated due to a weak interaction between these chains [3,4]. Therefore, those 1D materials have defect-free surfaces, high anisotropy, and carrier mobility. For example, TiS3 nanowires obtained by mechanical stripping have a large carrier mobility of about 10000 cm2·V−1·s−1 [5-7]. Fibrous phosphorus is also a new one-dimensional material with high carrier mobility (308 cm2·V−1·s−1) and rapid response time [8-10]. These one-dimensional materials are ideal for photovoltaic and photocatalytic applications.
The KP15 is considered to be a novel low-dimensional material with layered structure, high hole carrier mobility (1000 cm2·V−1·s−1), and highly anisotropic properties [11]. The photodetectors prepared with KP15 have a fast response time and are ideal materials for photovoltaic applications [12]. Based on our previous studies, KP15 is also a one-dimensional material with a defect-free surface [13,14]. This is beneficial for the development of high-performance nanodevices. Searching effective synthesis routes for nanoscale KP15 has become an urgent issue. Liquid-phase exfoliation is one of the most straightforward methods to prepare low-dimensional materials at a low cost and with simple processes and high flexibility. In this case, the surface of bulk materials is peeled off or corroded by physical or chemical reactions in a liquid medium, and finally low-dimensional materials are obtained. Based on the Hansen's empirical theory, the exfoliation efficiency of low-dimensional materials can be improved by adjusting the composition and type of solutions used in the liquid-phase exfoliation [15-17]. This theory has been successfully used for improving the exfoliation efficiency in several low-dimensional materials, such as carbon, graphene, metal oxides, and fibrous phosphorus. [18].
In a previous study, we exfoliated KP15 in alcohol; however, this method was still inefficient [13]. Herein, the Hansen's empirical theory was firstly introduced to improve the liquid-phase exfoliation efficiency of KP15 nanowires. In addition, Hansen solubility parameters (HSPs) for KP15 were also obtained in this work. By using a solution containing 50% water and 50% acetone, the exfoliation efficiency of KP15 was effectively improved. Our results show that 79% of the KP15 nanowires had thickness values below 50 nm and 60.9% of these nanowires had width values below 100 nm. The thinnest KP15 nanowires reached 5.1 nm and had smooth boundaries. Meanwhile, a strong temperature-dependent Raman response was found in exfoliated KP15 nanowires. This indicates a strong phonon–phonon coupling in KP15 nanowires, which favors non-invasive temperature measurements of KP15 nanodevices.
Methods
Synthesis of KP15 bulks
The KP15 bulks were prepared by the gas-phase transfer method. High-purity red phosphorus (1.370 g, 99.9999%) and metallic potassium (0.130 g, 97%) were mixed in a quartz tube. The temperature gradient in the quartz tube was 650 °C/400 °C and the heat treatment time was 12 h. After annealed, dark-red KP15 bulks were finally obtained.
Liquid exfoliation
For the liquid-exfoliation process, 1 mg of KP15 was mixed in 20 mL of solvent and ultrasonically processed at a power of 80 W in an ice bath for 6 h, followed by centrifugation at 2000 rpm for 20 min. For the samples with predetermined concentration, centrifugation was not used.
Measurement equipment
UV−visible spectrophotometry was performed by using a Shimadzu UV-3101PC system. Atomic force microscopy (AFM) tests were performed in a Multimode 8 system. The Raman tests were performed on a WITec alpha300 RA confocal Raman microscopy system. For the Raman tests, KP15 samples were spun on SiO2(300 nm)/Si substrates. The excitation wavelength used was 532 nm, the spot size was approx. 1 μm, and the laser power was kept below 20 μW. For low-temperature Raman measurements, a Linkam THMS600 cryostat cooled by liquid nitrogen was used to control the temperature. To prevent sample drift, SiO2 (300 nm)/Si substrates with tested KP15 samples were attached by fixtures to the Linkam THMS600 cryostat.
Results and Discussion
KP15 bulks, prepared by the gas-phase-transfer method, had a flat and smooth surface shown in Figure 1a. The X-ray diffraction patterns of the synthesized KP15 were both theoretically calculated and experimentally measured. The consistency between the two patterns shows that there is no impurity phase (Figure 1b), which confirms an excellent crystallization quality of the KP15 bulks.
![[2190-4286-13-69-1]](/bjnano/content/figures/2190-4286-13-69-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: (a) Optical microscopy result of KP15 bulks. (b) XRD results of KP15 bulks.
Figure 1: (a) Optical microscopy result of KP15 bulks. (b) XRD results of KP15 bulks.
Measurement of the absorption coefficient and the Hansen solubility parameters for KP15
According to the Hansen’s theory [19], the dispersed concentration C of a KP15 dispersion prepared by liquid exfoliation can be expressed by Equation 1 as follows.
where δD is the intermolecular dispersion force, δH is the intermolecular hydrogen bond; δP is the intermolecular polar force; δA,D, δA,P, δA,H are the Hansen solubility parameters (HSPs) of the solute; and δB,D, δB,P, δB,H are the HSPs of the solvent. Therefore, to get a high concentration of KP15 in dispersion, the HSPs of the solvent for the exfoliation of KP15 should be close to those of KP15. A weighted average method was used to calculate the HSPs of KP15. The concentration of KP15 was used as a weight factor for each suspension. This way, the HSPs of KP15 can be expressed according to Equation 2 [19].
where δi,sol are the HSPs of the solvent and C is the concentration of the KP15 dispersions. The Lambert–Beer law (Equation 3) was then used to measure the concentration of the KP15 dispersions:
where A is the absorbance, K is the absorption coefficient of the material, b is the absorbing layer thickness (which in this work is the width of the cuvette, i.e., 1 cm), and C is the concentration of the KP15 dispersions. The absorbance A and the absorption coefficient K are related to the wavelength of the incident light. To determine A and K, it is necessary to choose a specific incident wavelength. The bandgap of bulk KP15 is approx. 1.75 eV [20]. However, according to our previous study, with thickness reduction of the KP15 nanowires, a surface-state luminescence at 693 nm gradually dominates in the KP15 nanowire [14]. This could affect light absorption properties of KP15 due to its decreased size.
To avoid the generation of concentration error caused by the absorbance influence of the surface state, a wavelength (800 nm) which is far away from the bandgap of KP15 bulk and surface state in the KP15 nanowires was chosen. Some dispersions for which we predetermined the concentration were prepared to fit and determine the absorption coefficient K. Solutions of five different concentrations of KP15 dispersions in butyrolactone were prepared by liquid exfoliation with a predetermined concentration. UV−visible absorption spectra results are shown in Figure 2. The concentration linearly varies with absorbance. The slope of this fitted linear equation is 3.86 ± 0.13. This means that the absorption coefficient of KP15 is 3.86 ± 0.13 mL·mg−1·cm−1.
![[2190-4286-13-69-2]](/bjnano/content/figures/2190-4286-13-69-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Absorbance of predetermined KP15 dispersions exfoliated in butyrolactone. (a) Absorbance of different concentrations of predetermined KP15 dispersions exfoliated in butyrolactone. (b) Absorbance (800 nm) as a function of concentration of predetermined KP15 dispersions. The absorption coefficient (800 nm) is 3.86 ± 0.13 mL·mg−1·cm−1.
Figure 2: Absorbance of predetermined KP15 dispersions exfoliated in butyrolactone. (a) Absorbance of differe...
We selected 20 common solvents, including benzyl benzoate, toluene, ethyl acetate, acetone, alcohol, butyrolactone, N,N'-dimethylpropyleneurea, bromobenzene, cyclopentanone, N-dodecyl-2-pyrrolidone, glycol, vinyl acetate, hexane, isopropyl alcohol, N,N-dimethylformamide, O-phthalic dimethyl ester, dimethyl sulfoxide, N-methylpyrrolidone, water, and cyclohexanone. The HSPs of those solvents are listed in Table 1.
Table 1: Hansen parameters for the solvents [21].
| solvent | δD (MPa1/2) | δP (MPa1/2) | δH (MPa1/2) |
| benzyl benzoate | 20 | 5.1 | 5.2 |
| toluene | 18 | 1.4 | 2 |
| ethyl acetate | 15.8 | 5.3 | 7.2 |
| acetone | 15.5 | 10.4 | 7 |
| alcohol | 18.1 | 17.1 | 16.9 |
| butyrolactone | 18 | 16.6 | 7.4 |
| N,N'-dimethylpropyleneurea | 17.8 | 9.5 | 9.3 |
| bromobenzene | 19.2 | 5.5 | 4.1 |
| cyclopentanone | 17.9 | 11.9 | 5.2 |
| N-dodecyl-2-pyrrolidone | 17.5 | 4.1 | 3.2 |
| glycol | 17 | 11 | 26 |
| vinyl acetate | 16 | 7.2 | 5.9 |
| hexane | 14.9 | 0 | 0 |
| isopropyl alcohol | 15.8 | 6.1 | 16.4 |
| N,N-dimethylformamide | 17.4 | 13.7 | 11.3 |
| O-phthalic dimethyl ester | 18.6 | 10.8 | 4.9 |
| dimethyl sulfoxide | 18.4 | 16.4 | 10.2 |
| N-methylpyrrolidone | 18 | 12.3 | 7.2 |
| water | 15.8 | 8.8 | 19.4 |
| cyclohexanone | 17.8 | 8.4 | 5.1 |
Figure 3 exhibits the concentrations of KP15 dispersions exfoliated in different solvents. Cyclopentanone and butyrolactone were more suitable than the other solvents to exfoliate KP15. Figure 4 shows the relationship between the HSPs of different solvents and the concentration of the KP15 suspension. Based on Equation 2, the HSPs of KP15 were δD = 17.60 MPa1/2, δP = 11.19 MPa1/2, and δH = 8.95 MPa1/2. As long as the difference between the HSPs of KP15 and the HSPs of a given solvent is reduced, τ can be reduced with an improved exfoliation efficiency. Figure 5 shows the concentration of KP15 dispersions as a function of τ. When τ tends to zero, the concentration of the KP15 dispersion reaches the maximum value, which corresponds to the results of the aforementioned equation.
![[2190-4286-13-69-3]](/bjnano/content/figures/2190-4286-13-69-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: UV−visible spectrum of the KP15 dispersions using various solvents.
Figure 3: UV−visible spectrum of the KP15 dispersions using various solvents.
![[2190-4286-13-69-4]](/bjnano/content/figures/2190-4286-13-69-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: Concentration of KP15 dispersions as a function of the Hansen parameters. (a) Concentration of KP15 dispersions as a function of δD. (b) Concentration of KP15 dispersions as a function of δP. (c) Concentration of KP15 dispersions as a function of δH.
Figure 4: Concentration of KP15 dispersions as a function of the Hansen parameters. (a) Concentration of KP15...
![[2190-4286-13-69-5]](/bjnano/content/figures/2190-4286-13-69-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: Concentration of KP15 dispersions as a function of τ, τ = [(δA,D − δB,D)2 + (δA,P − δB,P)2/4 + (δA,H − δB,H)2/4].
Figure 5: Concentration of KP15 dispersions as a function of τ, τ = [(δA,D − δB,D)2 + (δA,P − δB,P)2/4 + (δA,H...
Liquid exfoliation of one-dimensional KP15
The HSPs obtained for KP15 were δD = 17.60 MPa1/2, δP = 11.19 MPa1/2, and δH = 8.95 MPa1/2. We chose a mixed solution containing water and acetone to exfoliate KP15. The HSPs of water were δD = 15.8 MPa1/2, δP = 8.8 MPa1/2, and δH = 19.4 MPa1/2. The HSPs of acetone were δD = 15.5 MPa1/2, δP = 10.4 MPa1/2, and δH = 7.0 MPa1/2. The HSP range of a mixed solution of water and acetone can cover the HSPs of KP15, however, both of them can be easily removed. The HSPs (δi) in a mixed solution containing water and acetone can be expressed by Equation 4.
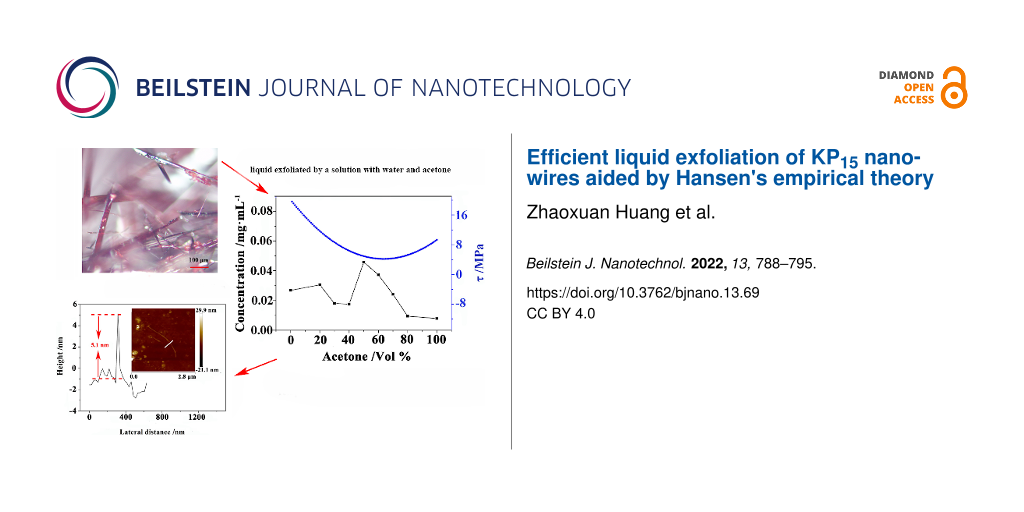
where ϕi,comp is the volume fraction of the corresponding solvent and δi,comp is the HSPs of the solvent. The concentration of the KP15 dispersion can be measured by the Lambert–Beer law (Equation 3). As shown in Figure 6a, by tuning the volume fraction of acetone in the mixed solution, the HSPs of the mixed solution can be close to those of KP15, and the exfoliation efficiency can be clearly improved. The concentration values of the KP15 suspension in the solutions were 0.0268 mg·mL−1 (exfoliated in deionized water), 0.0079 mg·mL−1 (acetone), and 0.0236 mg·mL−1 (alcohol), respectively [13]. When the solvent mixture with a 50% volume fraction of acetone is used for stripping, the concentration of the KP15 dispersion finally increases to 0.0458 mg·mL−1. At this point, the parameter τ is close to the minimum value.
![[2190-4286-13-69-6]](/bjnano/content/figures/2190-4286-13-69-6.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: Results of KP15 dispersions exfoliated in acetone/water mixtures. (a) Absorbance of KP15 dispersions exfoliated in acetone/water mixtures with different acetone volume fractions. (b) KP15 suspension concentration and the calculated τ as a function of the acetone volume fraction.
Figure 6: Results of KP15 dispersions exfoliated in acetone/water mixtures. (a) Absorbance of KP15 dispersion...
The Raman result for the KP15 nanowires exfoliated in water−acetone mixed solution is shown in Figure 7c. At least 11 distinguishable Raman peaks located at 476.6, 453.0, 408.8, 378.3, 368.4, 354.1, 303.7, 288.5, 126.1, 114.1, and 90.7 cm−1 were seen and those Raman results were similar to the Raman modes of mechanically exfoliated KP15 [11]. As shown in Figure 7d, Figure 7e, and Figure 8, the thinnest KP15 nanowires obtained by liquid exfoliation could reach 5.1 nm and had smooth boundaries. The thicknesses of 79% of the liquid-exfoliated KP15 nanowires were below 50 nm; the widths of 60.9% of the KP15 nanowires were below 100 nm. The sizes of the obtained KP15 nanowires were much smaller than those obtained in our previous studies [13]. Meanwhile, a strong temperature-dependent Raman response in exfoliated KP15 nanowires has been observed. That may help with non-invasive temperature measurements of KP15 nanodevices (details are demonstrated in Supporting Information File 1).
![[2190-4286-13-69-7]](/bjnano/content/figures/2190-4286-13-69-7.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 7: (a) Height distribution of KP15 nanowires after liquid exfoliation. (b) Cross sections of KP15 nanowires after liquid exfoliation. (c) Raman spectra of KP15 nanowires after liquid exfoliation. (d) Thickness histograms of KP15 nanowires after liquid exfoliation. (e) Width histograms of KP15 nanowires after liquid exfoliation.
Figure 7: (a) Height distribution of KP15 nanowires after liquid exfoliation. (b) Cross sections of KP15 nano...
![[2190-4286-13-69-8]](/bjnano/content/figures/2190-4286-13-69-8.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 8: Sizes of exfoliated KP15 nanowires. (a) Cross section of the KP15 nanowire marked in the upper right corner inset image. (b) Cross section of the KP15 nanowire marked in the upper right corner inset image. (c) Cross section of the KP15 nanowire marked in the upper right corner inset image. (d) Cross section of the KP15 nanowire marked in the upper right corner inset image.
Figure 8: Sizes of exfoliated KP15 nanowires. (a) Cross section of the KP15 nanowire marked in the upper righ...
Conclusion
In summary, based on the Hansen's empirical theory, the liquid phase exfoliation efficiency of KP15 nanowires has been improved. The HSPs of KP15 were calculated to be δD = 17.60 MPa1/2, δP = 11.19 MPa1/2, and δH = 8.95 MPa1/2. In addition, based on the Hansen's empirical theory, the exfoliation efficiency was improved by adjusting the ratio of water and acetone. When the mixed solvents had the smallest τ, the thicknesses of 79% of liquid-exfoliated KP15 nanowires were below 50 nm and the widths of 60.9% of KP15 nanowires were below 100 nm. Meanwhile, a strong temperature-dependent Raman response has been found in exfoliated KP15, which may help with non-invasive temperature measurements of KP15 nanodevices.
Supporting Information
| Supporting Information File 1: Strong temperature-dependent Raman response of exfoliated KP15. | ||
| Format: PDF | Size: 800.5 KB | Download |
Funding
This work was supported by the National Natural Science Foundation of China under the grant (51972006), Guangxi Key Laboratory of Optical and Electronic Materials and Devices (20AA-19), Guilin University of Technology research fund (GUTQDJJ2019031), Guangxi Young and middle-aged teachers' basic ability improvement project (2021KY0251), National Natural Science Foundation of China (U20A20245), Guangxi Distinguished Experts Special Fund (2019B06), Guangxi Research Foundation for Science and Technology Base and Talent Special (AD19245175), National Natural Science Foundation of China (NFSC) (52002318), and National Science Foundation of Shaanxi Province (2020JQ-841).
References
-
Yang, B.; Chen, J.; Liu, B.; Ding, Y.; Tang, Y.; Yan, X. J. Mater. Chem. A 2021, 9, 6352–6360. doi:10.1039/d1ta00404b
Return to citation in text: [1] -
Zhao, R.; Wei, Q.; Ran, Y.; Kong, Y.; Ma, D.; Su, L.; Yao, L.; Wang, Y. Nanotechnology 2021, 32, 375501. doi:10.1088/1361-6528/ac06f6
Return to citation in text: [1] -
Fei, B.; Chen, C.; Hu, C.; Cai, D.; Wang, Q.; Zhan, H. ACS Appl. Energy Mater. 2020, 3, 9018–9027. doi:10.1021/acsaem.0c01431
Return to citation in text: [1] -
Jiang, X.; Qin, S.; Cao, Y.; Wu, R.; Han, D.; Hua, Z.; Zhu, C.; Huang, X.; Wang, L.; Yang, S. ACS Appl. Nano Mater. 2020, 3, 3402–3409. doi:10.1021/acsanm.0c00152
Return to citation in text: [1] -
Island, J. O.; Buscema, M.; Barawi, M.; Clamagirand, J. M.; Ares, J. R.; Sánchez, C.; Ferrer, I. J.; Steele, G. A.; van der Zant, H. S. J.; Castellanos-Gomez, A. Adv. Opt. Mater. 2014, 2, 641–645. doi:10.1002/adom.201400043
Return to citation in text: [1] -
Dai, J.; Zeng, X. C. Angew. Chem. 2015, 127, 7682–7686. doi:10.1002/ange.201502107
Return to citation in text: [1] -
Island, J. O.; Barawi, M.; Biele, R.; Almazán, A.; Clamagirand, J. M.; Ares, J. R.; Sánchez, C.; van der Zant, H. S. J.; Álvarez, J. V.; D'Agosta, R.; Ferrer, I. J.; Castellanos-Gomez, A. Adv. Mater. (Weinheim, Ger.) 2015, 27, 2595–2601. doi:10.1002/adma.201405632
Return to citation in text: [1] -
Eckstein, N.; Hohmann, A.; Weihrich, R.; Nilges, T.; Schmidt, P. Z. Anorg. Allg. Chem. 2013, 639, 2741–2743. doi:10.1002/zaac.201300327
Return to citation in text: [1] -
Zhang, G.; Liu, D.; Tian, N.; Liu, B.; Li, S.; You, C.; Qu, X.; Ma, H.; Fan, C.; Zhang, Y. Inorg. Chem. 2020, 59, 976–979. doi:10.1021/acs.inorgchem.9b03188
Return to citation in text: [1] -
Smith, J. B.; Hagaman, D.; DiGuiseppi, D.; Schweitzer‐Stenner, R.; Ji, H.-F. Angew. Chem., Int. Ed. 2016, 55, 11829–11833. doi:10.1002/anie.201605516
Return to citation in text: [1] -
Tian, N.; Yang, Y.; Liu, D.; Liu, X.; Tan, P.-H.; Zhang, D.; Chang, K.; Li, H.; Zhao, M.; Li, J. R.; Tang, X.; Zhang, D.; Zhang, Z.; Xiao, W.; Yan, H.; Zhang, Y. ACS Nano 2018, 12, 1712–1719. doi:10.1021/acsnano.7b08368
Return to citation in text: [1] [2] -
Yang, Y.; Chen, X.; Tian, N.; Zhang, Y.; Liu, D.; Yan, H. Mater. Lett. 2020, 272, 127826. doi:10.1016/j.matlet.2020.127826
Return to citation in text: [1] -
Tian, N.; Liu, D.; Zhou, B.; Yang, Y.; Zhang, G.; Zhang, D.; Zhang, Y. Mater. Lett. 2018, 228, 89–91. doi:10.1016/j.matlet.2018.05.048
Return to citation in text: [1] [2] [3] [4] -
Tian, N.; Liu, D.; Yang, Y.; Zhang, G.; Zhang, D.; Zhang, Y. Nanoscale 2018, 10, 16479–16484. doi:10.1039/c8nr05766d
Return to citation in text: [1] [2] -
Alzakia, F. I.; Tan, S. C. Adv. Sci. 2021, 8, 2003864. doi:10.1002/advs.202003864
Return to citation in text: [1] -
Qin, J.; Wang, X.; Jiang, Q.; Cao, M. ChemPhysChem 2019, 20, 1069–1097. doi:10.1002/cphc.201900110
Return to citation in text: [1] -
Xie, Y.-M.; Yao, Q.; Xue, Q.; Zeng, Z.; Niu, T.; Zhou, Y.; Zhuo, M.-P.; Tsang, S.-W.; Yip, H.-L.; Cao, Y. Interdiscip. Mater. 2022, 1, 281–293. doi:10.1002/idm2.12023
Return to citation in text: [1] -
Zhang, G.; Liu, D.; Tian, N.; Wang, X.; Yan, W.; Huang, Z.; Zhang, Y. Inorg. Chem. 2021, 60, 4883–4890. doi:10.1021/acs.inorgchem.0c03791
Return to citation in text: [1] -
Hernandez, Y.; Lotya, M.; Rickard, D.; Bergin, S. D.; Coleman, J. N. Langmuir 2010, 26, 3208–3213. doi:10.1021/la903188a
Return to citation in text: [1] [2] -
Olego, D. J. Phys. Rev. B 1985, 31, 2230–2239. doi:10.1103/physrevb.31.2230
Return to citation in text: [1] -
Barton, A. F. M. CRC handbook of solubility parameters and other cohesion parameters; CRC Press: Boca Raton, FL, USA, 1991.
Return to citation in text: [1]
| 11. | Tian, N.; Yang, Y.; Liu, D.; Liu, X.; Tan, P.-H.; Zhang, D.; Chang, K.; Li, H.; Zhao, M.; Li, J. R.; Tang, X.; Zhang, D.; Zhang, Z.; Xiao, W.; Yan, H.; Zhang, Y. ACS Nano 2018, 12, 1712–1719. doi:10.1021/acsnano.7b08368 |
| 13. | Tian, N.; Liu, D.; Zhou, B.; Yang, Y.; Zhang, G.; Zhang, D.; Zhang, Y. Mater. Lett. 2018, 228, 89–91. doi:10.1016/j.matlet.2018.05.048 |
| 1. | Yang, B.; Chen, J.; Liu, B.; Ding, Y.; Tang, Y.; Yan, X. J. Mater. Chem. A 2021, 9, 6352–6360. doi:10.1039/d1ta00404b |
| 2. | Zhao, R.; Wei, Q.; Ran, Y.; Kong, Y.; Ma, D.; Su, L.; Yao, L.; Wang, Y. Nanotechnology 2021, 32, 375501. doi:10.1088/1361-6528/ac06f6 |
| 11. | Tian, N.; Yang, Y.; Liu, D.; Liu, X.; Tan, P.-H.; Zhang, D.; Chang, K.; Li, H.; Zhao, M.; Li, J. R.; Tang, X.; Zhang, D.; Zhang, Z.; Xiao, W.; Yan, H.; Zhang, Y. ACS Nano 2018, 12, 1712–1719. doi:10.1021/acsnano.7b08368 |
| 21. | Barton, A. F. M. CRC handbook of solubility parameters and other cohesion parameters; CRC Press: Boca Raton, FL, USA, 1991. |
| 8. | Eckstein, N.; Hohmann, A.; Weihrich, R.; Nilges, T.; Schmidt, P. Z. Anorg. Allg. Chem. 2013, 639, 2741–2743. doi:10.1002/zaac.201300327 |
| 9. | Zhang, G.; Liu, D.; Tian, N.; Liu, B.; Li, S.; You, C.; Qu, X.; Ma, H.; Fan, C.; Zhang, Y. Inorg. Chem. 2020, 59, 976–979. doi:10.1021/acs.inorgchem.9b03188 |
| 10. | Smith, J. B.; Hagaman, D.; DiGuiseppi, D.; Schweitzer‐Stenner, R.; Ji, H.-F. Angew. Chem., Int. Ed. 2016, 55, 11829–11833. doi:10.1002/anie.201605516 |
| 13. | Tian, N.; Liu, D.; Zhou, B.; Yang, Y.; Zhang, G.; Zhang, D.; Zhang, Y. Mater. Lett. 2018, 228, 89–91. doi:10.1016/j.matlet.2018.05.048 |
| 5. | Island, J. O.; Buscema, M.; Barawi, M.; Clamagirand, J. M.; Ares, J. R.; Sánchez, C.; Ferrer, I. J.; Steele, G. A.; van der Zant, H. S. J.; Castellanos-Gomez, A. Adv. Opt. Mater. 2014, 2, 641–645. doi:10.1002/adom.201400043 |
| 6. | Dai, J.; Zeng, X. C. Angew. Chem. 2015, 127, 7682–7686. doi:10.1002/ange.201502107 |
| 7. | Island, J. O.; Barawi, M.; Biele, R.; Almazán, A.; Clamagirand, J. M.; Ares, J. R.; Sánchez, C.; van der Zant, H. S. J.; Álvarez, J. V.; D'Agosta, R.; Ferrer, I. J.; Castellanos-Gomez, A. Adv. Mater. (Weinheim, Ger.) 2015, 27, 2595–2601. doi:10.1002/adma.201405632 |
| 3. | Fei, B.; Chen, C.; Hu, C.; Cai, D.; Wang, Q.; Zhan, H. ACS Appl. Energy Mater. 2020, 3, 9018–9027. doi:10.1021/acsaem.0c01431 |
| 4. | Jiang, X.; Qin, S.; Cao, Y.; Wu, R.; Han, D.; Hua, Z.; Zhu, C.; Huang, X.; Wang, L.; Yang, S. ACS Appl. Nano Mater. 2020, 3, 3402–3409. doi:10.1021/acsanm.0c00152 |
| 14. | Tian, N.; Liu, D.; Yang, Y.; Zhang, G.; Zhang, D.; Zhang, Y. Nanoscale 2018, 10, 16479–16484. doi:10.1039/c8nr05766d |
| 18. | Zhang, G.; Liu, D.; Tian, N.; Wang, X.; Yan, W.; Huang, Z.; Zhang, Y. Inorg. Chem. 2021, 60, 4883–4890. doi:10.1021/acs.inorgchem.0c03791 |
| 19. | Hernandez, Y.; Lotya, M.; Rickard, D.; Bergin, S. D.; Coleman, J. N. Langmuir 2010, 26, 3208–3213. doi:10.1021/la903188a |
| 15. | Alzakia, F. I.; Tan, S. C. Adv. Sci. 2021, 8, 2003864. doi:10.1002/advs.202003864 |
| 16. | Qin, J.; Wang, X.; Jiang, Q.; Cao, M. ChemPhysChem 2019, 20, 1069–1097. doi:10.1002/cphc.201900110 |
| 17. | Xie, Y.-M.; Yao, Q.; Xue, Q.; Zeng, Z.; Niu, T.; Zhou, Y.; Zhuo, M.-P.; Tsang, S.-W.; Yip, H.-L.; Cao, Y. Interdiscip. Mater. 2022, 1, 281–293. doi:10.1002/idm2.12023 |
| 19. | Hernandez, Y.; Lotya, M.; Rickard, D.; Bergin, S. D.; Coleman, J. N. Langmuir 2010, 26, 3208–3213. doi:10.1021/la903188a |
| 13. | Tian, N.; Liu, D.; Zhou, B.; Yang, Y.; Zhang, G.; Zhang, D.; Zhang, Y. Mater. Lett. 2018, 228, 89–91. doi:10.1016/j.matlet.2018.05.048 |
| 14. | Tian, N.; Liu, D.; Yang, Y.; Zhang, G.; Zhang, D.; Zhang, Y. Nanoscale 2018, 10, 16479–16484. doi:10.1039/c8nr05766d |
| 12. | Yang, Y.; Chen, X.; Tian, N.; Zhang, Y.; Liu, D.; Yan, H. Mater. Lett. 2020, 272, 127826. doi:10.1016/j.matlet.2020.127826 |
| 13. | Tian, N.; Liu, D.; Zhou, B.; Yang, Y.; Zhang, G.; Zhang, D.; Zhang, Y. Mater. Lett. 2018, 228, 89–91. doi:10.1016/j.matlet.2018.05.048 |
© 2022 Huang et al.; licensee Beilstein-Institut.
This is an open access article licensed under the terms of the Beilstein-Institut Open Access License Agreement (https://www.beilstein-journals.org/bjnano/terms), which is identical to the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0). The reuse of material under this license requires that the author(s), source and license are credited. Third-party material in this article could be subject to other licenses (typically indicated in the credit line), and in this case, users are required to obtain permission from the license holder to reuse the material.