Abstract
High-resolution vacuum ultraviolet photoabsorption measurements in the wavelength range of 115–320 nm (10.8–3.9 eV) have been performed together with comprehensive relativistic time-dependent density functional calculations (TDDFT) on the low-lying excited sates of tungsten hexacarbonyl, W(CO)6. The higher resolution obtained reveals previously unresolved spectral features of W(CO)6. The spectrum shows two higher-energy bands (in the energy ranges of 7.22–8.12 eV and 8.15–9.05 eV), one of them with clear vibrational structure, and a few lower-energy shoulders in addition to a couple of lower-energy metal-to-ligand charge-transfer (MLCT) bands reported in the literature before. Absolute photoabsorption cross sections are reported and, where possible, compared to previously published results. On the basis of this combined experimental/theoretical study the absorption spectrum of the complex has been totally re-assigned between 3.9 and 10.8 eV under the light of spin–orbit coupling (SOC) effects. The present comprehensive knowledge of the nature of the electronically excited states may be of relevance to estimate neutral dissociation cross sections of W(CO)6, a precursor molecule in focused electron beam induced deposition (FEBID) processes, from electron scattering measurements.
Introduction
The electronic structure of tungsten hexacarbonyl, W(CO)6, has previously been studied by using a variety of different experimental and theoretical methods, with experiments including vacuum ultraviolet experiments in the wavelength range of 125–350 nm [1-5], and electron energy loss [6-8], photoelectron [9,10], photoionisation [11] and electron momentum [12,13] spectroscopy. In theoretical studies, Dirac-scattered-wave (DSW) calculations [14], molecular orbital energy level calculations [2], relativistic time-dependent density functional theory (TDDFT) calculations [15], and electron momentum spectroscopy calculations [16] have been carried out. Other relevant studies include DFT calculations on the structure of W(CO)6 and its behaviour in infrared spectroscopy [17], as well as Raman [18] and infrared [18-20] spectroscopy experiments. Detailed knowledge of the electronic-state spectroscopy of transition-metal hexacarbonyls has attracted particular attention due to the ability of CO to form complexes with metals in low oxidation states. This is possible due to the presence of low-lying empty π*-orbitals, which play a significant role in the stability of carbonyl complexes, and in particular for W(CO)6 where the tungsten oxidation state is zero. W(CO)6 is a precursor molecule used in electron beam induced deposition (EBID) to produce well-defined tungsten-containing nanostructures [21,22]. Nanometre-thick films of surface-adsorbed W(CO)6 irradiated at 500 eV electron impact energy were analysed in situ by X-ray photoelectron spectroscopy (XPS), mass spectrometry and reflective absorption infrared spectroscopy (RAIRS) measurements [23]. These studies on electron-stimulated reactions of surface-adsorbed W(CO)6 molecules have shown contaminations by C and O due to incomplete ligand desorption yielding tungsten oxide and an enhanced degree of tungsten oxidation from the presence of co-adsorbed water. These contaminations are then incorporated into the carbonaceous matrix. Recently, we note ab initio molecular dynamics simulations of focused electron beam induced deposition (FEBID) precursor molecules adsorbed on fully and partially hydroxylated SiO2 surfaces [24]. Electron-induced reactions in FEBID processes are initiated by low-energy secondary electrons rather than the high-energy primary beam impinging on the surface where dissociative electron attachment (DEA) processes are relevant, although at those energies electron impact excitations yielding neutral dissociation are prevalent in detriment to DEA [25]. Gas-phase DEA studies in the electron energy range from 0 to 14 eV reported by Wnorowski et al. [26] revealed the strong dissociation character of W(CO)6, with no formation of bare W− metal anions. Negative ion states of transition-metal hexacarbonyls have been obtained by electron transmission spectroscopy (ETS) with W(CO)6 attachment energies of 1.53, 2.46 and 4.26 eV [27]. We note electron impact ionisation studies on the appearance energies of bare tungsten hexacarbonyl [28], on the fragmentation pathways of W(CO)6 clusters [29] and on the complete ligand loss of weakly bound W(CO)6 dimer [30]. As far as neutral dissociation (ND) is concerned, Zlatar et al. [25] have reported on the relevance of electronically excited precursors yielding neutral fragmentation, although the products of ND processes appear to be more difficult to monitor than charged products in mass spectrometry. Therefore, detailed knowledge of the nature of the electronically excited states by experimental and theoretical methods are also demanded to assess the nature of the excited states from which estimates of ND cross sections can be obtained from electron energy loss spectroscopy. From the experimental point of view, such electron impact excitation spectra cannot be recorded with higher energy resolution than with optical spectra [31], making the latter an important tool to uncover features that may be not attained even in pseudo-optical conditions (high electron impact energy and low scattering angle) [32]. Another relevant aspect highlighted by Qi et al. [5] in the 30–160 nm wavelength region pertains to the similarity observed in the qualitative behaviour of neutral photodissociation and UV photoabsorption below the first ionisation energy, where CO ligand ejection occurs. Moreover, Venkataraman and co-workers [33] explored the photodissociation of W(CO)6 at 248 nm (ca. 5 eV) assigning the first CO elimination to a translational energy release process. As part of an ongoing effort to fully characterize the electron-induced fragmentation channels of W(CO)6, as needed for FEBID simulations, the purpose of the present work is to provide a high-resolution vacuum ultraviolet (VUV) absorption spectrum, representative of transition-metal carbonyl complexes for which unresolved spectral features remain to be solved, with a description as complete as possible of the electronic states.
In the next section we provide details on the experimental and theoretical methods used in this study for W(CO)6 followed by the results together with a discussion and comparison with previous data where possible. Finally, some concluding remarks that can be drawn from this study are given.
Experimental and Theoretical Methods
High-resolution vacuum ultraviolet photoabsorption
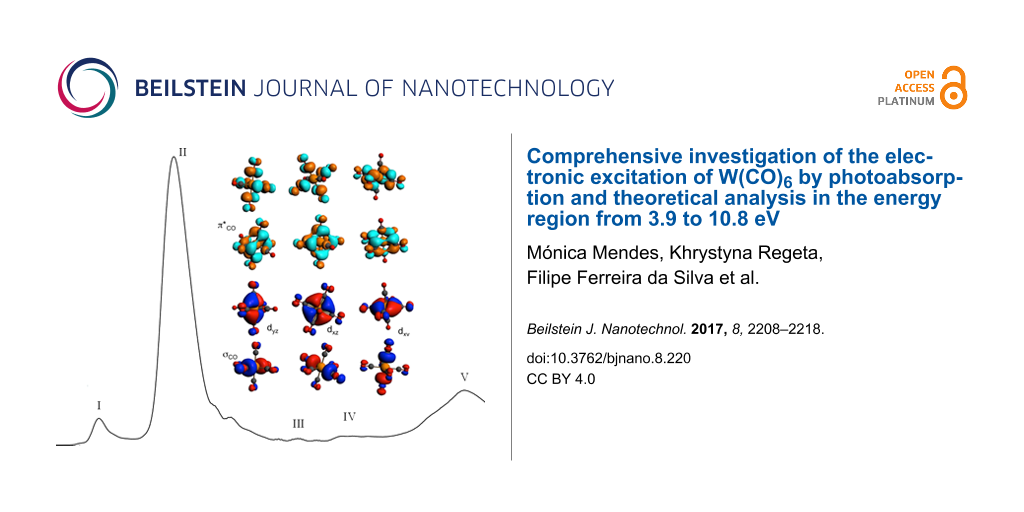
The high-resolution VUV photoabsorption studies of W(CO)6 in the photon energy range of 3.9–10.8 eV (Figure 1) were performed at the AU-UV beam line of the ASTRID2 synchrotron facility, Aarhus University, Denmark. The experimental setup has been described previously [31], with recent modifications reported in detail by Palmer et al. [34]. Briefly, an absorption gas cell is fitted with a heated 1 Torr full-scale Baratron capacitance manometer (Setra model 774) and a photo-multiplier tube (PMT) detector to measure the transmitted light intensity. In order to ensure that the data is free of any saturation effects, tungsten hexacarbonyl absorption cross sections were measured at an appropriate pressure with typical attenuations of less than 40%. The vacuum ultraviolet light exits the absorption cell through a MgF2 transmission window, which sets the lower limit of detectable light to 115 nm. A small gap between the PMT and the absorption cell is evacuated using a scroll pump to prevent any absorption of oxygen from the air for measurements below 200 nm (energies above 6.20 eV). For measurements above 220 nm, air is allowed into this gap to let oxygen absorb higher harmonics of light (at half the chosen wavelength) that may be passing through the cell.
![[2190-4286-8-220-1]](/bjnano/content/figures/2190-4286-8-220-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: High-resolution VUV photoabsorption spectrum of W(CO)6 in the photon energy range of 3.9–10.8 eV. The blue curve has the (right) ordinate set to a maximum of 50 Mb to bring out the rich fine structure in the spectrum.
Figure 1: High-resolution VUV photoabsorption spectrum of W(CO)6 in the photon energy range of 3.9–10.8 eV. T...
Absolute photoabsorption cross sections (in units of megabarn, 1 Mb ≡ 10−18 cm2) are obtained using the Beer–Lambert attenuation law It = I0·exp(−nσx), where It is the radiation intensity transmitted through the gas sample, I0 is the radiation intensity transmitted through the evacuated cell, n is the molecular number density of the sample gas, σ is the absolute photoabsorption cross section, and x is the absorption path length (here 15.5 cm). ASTRID2 is operated in a “top-up” mode, keeping the stored electron beam current (and thus the intensity for a given wavelength) quasi-constant, which is achieved by adding small amounts of current to the storage ring to make up for the constant beam decay. This procedure causes the beam current to vary by about 3% during a scan, with this effect being compensated for by a normalization of the data to an accurately determined beam current. The accuracy of the cross section is estimated to be better than ±5%. Only when the sample absorbs very weakly (I0 ≈ It), does the error increase as a percentage of the measured cross section.
Computational details
The structure of W(CO)6 has been fully optimized under the Oh symmetry constraint at the density functional theory (DFT) level with B3LYP functional [35] with all electron and triple-ζ polarized basis sets in vacuum [36], leading to W–C and C–O bond lengths of 2.069 Å and 1.144 Å (1.141 Å from [15]), respectively. The metal bond length is slightly overestimated with respect to previous results yielding a W–C bond length between 2.047 and 2.063 Å [37]. However, the agreement is reasonable knowing that B3LYP overestimates metal–carbonyl bond lengths. The scalar relativistic effects have been included within the zero-order regular approximation (ZORA) [38]. The vertical spin-free absorption spectrum based on the 80 lowest excited states has been computed by means of time-dependent density functional theory (TDDFT) [39,40]. Spin–orbit coupling (SOC) effects have been applied as a perturbation to obtain the “spin–orbit” states. All calculations have been performed in vacuum with the ADF2013 code [41]. The computational protocol is based on our experience in the field of excited states of transition-metal complexes. In particular, the choice of B3LYP functional has been dictated by the good results obtained with 25% of XC in a number of transition-metal complexes characterized by a variety of excited states of different character. In contrast, CAM-B3LYP, which has been parametrized for small transition-metal compounds with different electronic properties more atomic-like, gives systematic overestimations of transition energies in the complexes [42-48].
Tungsten hexacarbonyl sample
The sample used in the photoabsorption measurements was purchased from Sigma-Aldrich, with a stated purity of ≥99%. The sample was used as delivered.
Results and Discussion
Tungsten hexacarbonyl spectroscopy
W(CO)6 belongs to the Oh point group with the calculated electronic configuration of the outermost valence orbitals for the ground state 1A1g being (7eg)4 (3t2g)6 (1t1g)6 (11t1u)6 (4t2g)6, and only optically allowed 1A1g→1T1u transitions. The analysis of the ground-state Kohn–Sham (KS) orbitals (Figure 2 and Figure S1 in Supporting Information File 1) shows that the highest occupied molecular orbital (HOMO), 4t2g, has metal dπ character, the second-highest molecular orbital (HOMO−1), 11t1u, has σCO character, the third-highest (HOMO−2), 1t1g, and the fourth-highest occupied molecular orbitals (HOMO−3), 3t2g, have CO character. The lowest unoccupied molecular orbital (LUMO), 12t1u, and (LUMO+1), 3t2u, have mainly π*CO antibonding character, while (LUMO+2), 13t1u, and (LUMO+3), 2t1g, have π*CO and σ*CO character, respectively.
![[2190-4286-8-220-2]](/bjnano/content/figures/2190-4286-8-220-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Valence Kohn–Sham orbitals of W(CO)6 in its electronic ground state.
Figure 2: Valence Kohn–Sham orbitals of W(CO)6 in its electronic ground state.
Interpretation of the experimental data and results from quantum chemical calculations of the lowest electronic states with spin–orbit coupling (SOC) are summarised in Table 1. Singlet and triplet excited state energies without SOC are reported in Table S1 and Table S2 of Supporting Information File 1. The calculated transition energies reported in Table 1 are generally within 0.1–0.2 eV when compared with the experiment, with the exception of the strongest absorption band where the difference amounts to an overestimation of 0.5 eV. Nonetheless, this level of accuracy is reasonable for describing the VUV photoabsorption features. The TDDFT absorption spectrum of W(CO)6 without SOC is depicted in Figure S2 of Supporting Information File 1.
Table 1: TDDFT vertical transition energies and associated oscillator strengths (f0) of the low-lying “spin–orbit” excited states of W(CO)6 and assignment of the experimental spectrum.
|
energya
(eV) |
cross section
(Mb) |
band | state | composition in “spin-free” statesb |
calculated energy
(eV) |
f0 | character |
| <4.0 | 1T1u | 72% 13T1u 19% 13Eu | 3.458 | 3.7·10−4 | MLCT | ||
| 2T1u | 40% 13Eu 33% 13T2u 26% 13T1u | 3.596 | 1.2·10−4 | MLCT | |||
| 3T1u | 59% 13T2u 40% 13Eu | 3.656 | 4.1·10−5 | MLCT | |||
| 4.317 | 39.4 | I | 4T1u | 91% 11T1u | 4.11 | 0.02 | MLCT |
| 6T1u | 40% 23T1u 38% 13A1u 15% 23Eu | 4.309 | 0.002 | MLCT/IL | |||
| 5.590 | 377.7 | II | 9T1u | 99% 21T1u | 6.106 | 0.93 | MLCT |
| 7.630 | 13.2 | III | 10T1u | 99% 33T1u | 7.965 | 3.2·10−5 | IL |
| 8.35(5) | 16.2 | IV | 11T1u | 27% 33Eu 25% 31T1u 24% 43T1u 23% 33T2u | 8.146 | 0.009 | MLCT |
| 12T1u | 38% 33T2u 37% 43T1u 13% 31T1u 12% 33Eu | 8.264 | 0.005 | MLCT | |||
| 13T1u | 36% 33Eu 32% 43T1u 19% 33T2u 13% 31T1u | 8.329 | 0.004 | MLCT | |||
| 14T1u | 49% 31T1u 25% 33Eu 20% 33T2u | 8.340 | 0.017 | MLCT | |||
| 10.375 | 75.5 | V | 21T1u | 85% 41T1u 14% 63T1u | 10.011 | 0.057 | IL |
| 22T1u | 79% 63T1u 14% 41T1u | 10.036 | 0.009 | IL | |||
| 24T1u | 64% 73T1u 31% 51T1u | 10.211 | 0.012 | IL | |||
| 25T1u | 59% 51T1u 31% 73T1u | 10.242 | 0.021 | IL | |||
| 27T1u | 37% 33A1u 30% 71T1u 17% 61T1u | 10.456 | 0.027 | IL | |||
| 30T1u | 60% 61T1u 20% 71T1u | 10.524 | 0.017 | IL | |||
| 32T1u | 32% 71T1u 27% 73Eu 20% 33A1u | 10.557 | 0.027 | IL | |||
| 33T1u | 43% 73Eu 39% 83Eu | 10.632 | 0.004 | IL | |||
| 34T1u | 52% 83Eu | 10.701 | 0.008 | IL | |||
| 36T1u | 57% 81T1u 22% 93T1u | 10.867 | 0.026 | SBLCT | |||
| 37T1u | 38% 81T1u 33% 93T1u | 10.889 | 0.021 | SBLCT | |||
aThe last decimal of the energy value is given in parenthesis for these less-resolved features. bAccording to the labels of the states reported in Table S1 and Table S2 of Supporting Information File 1.
Valence transitions
The measured high-resolution VUV photoabsorption spectrum is presented in Figure 1, in the photon energy range from 3.9 to 10.8 eV, and the proposed assignments are summarised in Table 1 based on the vibrational spectra of Amster et al. [18], Broquier et al. [19] and the infrared data of Jones [20]. The main features have been identified as bands I to V and their main characteristics are discussed below, with a complete overview and assignment of the electronic structure. The TDDFT calculations with SOC predict an important contribution of the triplet states for bands III and IV as discussed further in the next sections.
A. Low-lying electronic states (below 4.0 eV)
The temperature-dependent absorption studies of Beach and Gray [2] of W(CO)6 in a solvent report a weak band at 3.794 eV, which was assigned to a spin-forbidden d→d transition. In contrast, our calculations do not provide evidence for the presence of low-lying metal-centred (MC) states in this period 6 transition-metal carbonyl complex, as it is the case in the period 4 analogue Cr(CO)6 [49]. The electron energy loss spectrum under non-dipolar conditions of Koerting and co-workers [6] reports a feature at 3.75 eV, which was assigned to a symmetry-forbidden feature. Rosa and co-workers [15] have proposed that in the region of 3.5–4.0 eV spin-allowed but symmetry-forbidden charge-transfer transitions as well as spin-forbidden but orbital-allowed 1A1g→a,b3T1u transitions occur. The present calculations including SOC effects show that three “spin–orbit” states, namely 1T1u, 2T1u and 3T1u of metal-to-ligand charge transfer (MLCT) character, which are composed essentially of 13T1u, 13Eu and 13T2u states, contribute to this region (Table 1 and Table S1 in Supporting Information File 1).
B. Band I (3.9–4.8 eV/330–260 nm)
The photoabsorption spectrum in the energy region of 3.9–4.8 eV is shown in Figure 3 and the proposed assignments are summarised in Table 2.
![[2190-4286-8-220-3]](/bjnano/content/figures/2190-4286-8-220-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: High-resolution VUV photoabsorption spectrum of W(CO)6 in the photon energy range of 3.9–5.0 eV. See text for details on the assignments.
Figure 3: High-resolution VUV photoabsorption spectrum of W(CO)6 in the photon energy range of 3.9–5.0 eV. Se...
The main absorption feature peaking at 4.317 eV with a local cross section of 39.4 Mb is assigned to the “spin–orbit” 4T1u state composed mainly of the 11T1u←11A1g transition involving the contribution from 12t1u←4t2g (0.66) and 3t2u←4t2g (0.33) of MLCT character and calculated to be at 4.119 eV (Table 1) in agreement with previous assignments. Indeed, this band has been identified by Gray and Beach [1] to MLCT at 4.328 eV, 4.32 eV by Koerting et al. [6], 4.36 eV by Cooper et al. [7], 4.30 eV by Pradeep [8] and 4.336 eV by Trogler and co-workers [4]. Rosa et al. [15] employing a combined TD-DFT/ZORA method, but without SOC effects, obtained a transition energy at 3.80 eV. Another interesting aspect is that ETS studies have reported a negative ion state at 4.26 eV [27], which can certainly be related to the main feature in the energy region of 3.9–4.8 eV.
The (0–0) origin band is not pronounced in the spectrum, although tentatively estimated to be at 4.04(6) eV (Table 2), according to the assignment on the vibrational structure reported by Trogler and co-workers [4]. The assignments of Gray and Beach [1,2] were based on electronic transitions at 4.039 and 4.609 eV assigned to 1T1g←1A1g and 1T2g←1A1g and expected to be weak because of a dipole-forbidden nature. Note that the electron energy loss spectroscopy data only reports the 1T2g←1A1g transition at 4.54 eV.
Table 2: Proposed vibrational assignments in the 4.0−9.0 eV absorption bands of W(CO)6. (b) broad structure; (s) shoulder structure; (w) weak feature. The last decimal of the energy value is given in brackets for these less-resolved features).
|
energy
(eV) |
assignment |
Δ(ν′2)
(eV) |
Δ(ν′1)
(eV) |
|---|---|---|---|
| band I | |||
| 4.04(6) (b,s) |
|
— | — |
| 4.317 |
|
— | 0.271 |
| 4.60(2) (s) |
|
— | 0.285 |
| band II | |||
| 6.15(6) (s) |
|
— | — |
| 6.19(6) (s) |
|
0.040 | — |
| 6.24(3) (s) |
|
0.047 | — |
| 6.29(7) (s) |
|
0.054 | — |
| 6.42(4) (w) |
|
— | 0.228 |
| 6.471 |
|
0.047 | 0.228 |
| 6.515 |
|
0.044 | 0.218 |
| 6.567 |
|
0.052 | — |
| 6.79(4) (b) |
|
— | 0.227 |
| band III | |||
| 7.16(7) (w,b) |
|
— | — |
| 7.208 |
|
0.041 | — |
| 7.259 |
|
0.051 | — |
| 7.315 |
|
0.056 | — |
| 7.358 |
|
0.043 | — |
| 7.41(1) (b) |
|
0.053 | 0.244 |
| 7.496 |
|
— | 0.237 |
| 7.542 |
|
0.046 | — |
| 7.583 |
|
0.041 | — |
| band III | |||
| 7.630 |
|
0.047 | 0.219 |
| 7.672 |
|
0.042 | — |
| 7.720 |
|
0.048 | 0.224 |
| 7.76(4) (s) |
|
0.044 | — |
| 7.80(8) (b) |
|
0.044 | — |
| 7.813 |
|
— | — |
| 7.862 |
|
0.049 | 0.232 |
| 7.907 |
|
0.045 | — |
| 7.948 |
|
0.041 | 0.228 |
| 7.994 |
|
0.046 | — |
| 8.03(5) (b) |
|
0.041 | — |
| Band IV | |||
| 8.098 |
|
— | — |
| 8.16(0) (s) |
|
0.062 | — |
| 8.21(1) (s) |
|
0.051 | — |
| 8.26(0) (s) |
|
0.049 | — |
| 8.30(4) (s) |
|
0.044 | — |
| 8.35(5) (b) |
|
0.051 | 0.257 |
| 8.38(9) (b) |
|
— | 0.178 |
| 8.574 |
|
— | 0.219 |
| 8.60(4) (s) |
|
— | 0.215 |
| 8.79(9) (b) |
|
— | 0.225 |
| 8.85(6) (w) |
|
— | 0.252 |
The calculations of Rosa et al. [15] assign this feature to the close-lying 1A1g→a1T1g and 1A1g→a1T2g symmetry-forbidden charge-transfer transitions. However, on the basis of the present calculations it seems that these symmetry-forbidden transitions do not participate in this band. In contrast, the mixed MLCT/intra-ligand (IL) 6T1u “spin–orbit” state calculated at 4.309 eV, with a modest oscillator strength (0.002) and composed essentially of 23T1u, 13A1u and 23Eu (Table 1), should contribute significantly. The present assignments are therefore based on a weak vibrational progression of the CO stretching mode ν1, with 0.263 eV (2124 cm−1) in the ground state [20], although an average of 0.278 eV is observed in Table 2 and is certainly due to the broad and shoulder nature of the experimental features.
C. Band II (5.0–7.0 eV/248–177 nm)
The photoabsorption spectrum of band II is shown in Figure 1 and our spectral assignments are shown in Table 2 and Figure 4. This is the most intense band within the photon energy range studied and corresponds mostly to the 21T1u←11A1g MLCT transition involving the contribution from (3t2u←4t2g) (0.64) and (12t1u←4t2g) (0.31) (Table 1) calculated at 6.106 eV with a large oscillator strength (0.93), and peaking in the experimental spectrum at 5.590 eV. This electronic excitation value is consistent with Gray and Beach [1,2] at 5.535 eV, Iverson and Russell [3] at 5.56 eV, Trogler et al. [4] at 5.391 eV, Koerting et al. [6] and Cooper et al. [7] at 5.5 eV, Pradeep [8] at 5.4 eV and Rosa et al. [15] at 5.84 eV. The main absorption feature has a local cross section of 377.7 Mb compared to 35.3 Mb from ref. [3] and on the high-energy side shows fine structure reminiscent of vibrational progressions involving the predominantly CO stretching mode ν1, and WC stretching mode ν2 (Table 2). The ν1-mode excited state frequency appears to drop by about 53 meV (to 0.225 eV) from Band I and the ν2-mode has an average excitation energy of 0.047 eV, which may be compared to 0.052 eV (392 cm-1) in the ground state [4,20]. Gray and Beach [1] assigned features at 6.263 and 6.526 eV to t2g(π)→t2g(π*) transitions, whereas Koerting et al. [6] at 6.24 and 6.54 eV report them as ligand-field (LF) 1A1g→1A1g symmetry forbidden transitions.
![[2190-4286-8-220-4]](/bjnano/content/figures/2190-4286-8-220-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: High-resolution VUV photoabsorption spectrum of W(CO)6 in the photon energy range of 6.0–9.0 eV. See text for details on the assignments.
Figure 4: High-resolution VUV photoabsorption spectrum of W(CO)6 in the photon energy range of 6.0–9.0 eV. Se...
It is interesting to note that in [9] an identical assignment was proposed for the feature at 6.51 eV while the calculation of Rosa et al. [15] only predicts LF transitions at higher energies, i.e., 7.33 and 7.44 eV but of T1g and T2g character. Our calculations do not support these assignments but rather singlet-to-triplet excitations of Rosa’s character (T1g and T2g) but at lower energies (see Table S2, Supporting Information File 1).
The photodissociation mechanisms of W(CO)6 have been investigated in a crossed laser–molecular beam study at 248 nm (ca. 5 eV), exploring the velocity distributions of the nascent photofragment yields [33]. A detailed analysis of the TOF photofragment distributions has provided a reliable description of the photodissociation mechanism for all six CO elimination steps required to produce the bare metal atom [33]. The single-photon and multiphoton processes yield sequential metal-to-ligand bond breaking with CO translational energy distributions assigned to direct and statistical dissociation, where the repulsive energy release in the first CO elimination step is expected to prevail in the condensed phase.
D. Band III (7.0–8.0 eV/177–155 nm)
The photoabsorption spectrum of band III can be seen in Figure 1 and Figure 4. Within this region we find the richest fine structure. The electronic absorption band that is the weakest over the whole energy range peaks at 7.630 eV with a local maximum cross section of 13.2 Mb in contrast to 7.65 eV and 1.56 Mb from Iverson and Russell [3]. It corresponds to a 33T1u←11A1g transition involving the contribution from 12t1u←1t1g (0.27), 3t2u←1t1g (0.16), (12t1u←3t2g (0.16) and 3t2u←3t2g (0.11) calculated at 7.965 eV (Table 1). The calculation suggests that the transition is due to IL electronic excitation. Koerting et al. [6] have assigned the feature at 7.66 eV to the 1A1g→1A1g symmetry-forbidden transition, where Cooper et al. [7] reported this at 7.48 eV. Transitions to singlet states from the ground state are symmetry-forbidden, but can gain some intensity through vibronic coupling [50,51]. Although our calculations do not predict an excitation to a singlet state for band III, the considerable rich fine structure may be responsible for making this absorption band, although weak, noticeable. Here, we report for the first time a comprehensive assignment of the features that involve excitation of the CO stretching mode ν1, and WC stretching mode ν2 (see Figure 4 and Table 2). The (0–0) origin band is tentatively estimated to be at 7.16(7) eV (Table 2) and the average energies of modes ν1 and ν2 are 0.231 and 0.046 eV, respectively. Rosa et al. [15] calculated the singlet LF states c1T1g and d1T2g at 7.33 and 7.44 eV, respectively, and the corresponding triplet states c3T1g and d3T2g at 7.09 and 7.19 eV, respectively. Our calculations predict two 3MC states, namely 3T2g and 3T1g calculated at 7.08 and 6.96 eV, respectively (Table S2 of Supporting Information File 1).
E. Band IV (8.0–9.0 eV/155–138 nm)
The photoabsorption spectrum of band IV is presented in Figure 4, with the spectral assignments being contained in Table 2. It has been assigned to a transition involving the contribution of (0.49) 31T1u/(0.25) 33E/(0.20) 33T2u from the electronic ground state (13t1u←4t2g) (0.92) (Table 1) calculated at 8.340 eV, peaking at 8.35(5) eV with a maximum cross section of 16.2 Mb. Three other transitions calculated at 8.146, 8.264 and 8.329 eV composed essentially of 33Eu, 33T2u and 33T1u (Table 1) may contribute to this band. The vacuum ultraviolet spectrum of Iverson and Russell report a value at 8.43 eV and a cross section value of 1.7 Mb [3]. The pseudo-photon measurements of Koerting et al. [6] and Cooper et al. [7] report values at 8.38 and 8.25 eV. The electron energy loss measurements assigned this transition to a symmetry-forbidden 1A1g→1A1g transition [6,7], in contrast to our assignment. The main absorption features within this band have been identified as having MLCT character. The origin of the band is placed at 8.098 eV (Table 2) and the fine structure has been assigned as combinations of the CO stretching mode ν1 (average value of 0.224 eV), and WC stretching mode ν2 (average value of 0.051 eV). The lowest-lying vertical ionisation energy of tungsten hexacarbonyl has been reported by Lloyd and Schlag [11] at 8.38 eV and the significant rise in the absorption spectrum signal above this energy may accommodate contributions from the ionic state.
F. Band V (above 9 eV)
Tungsten hexacarbonyl displays a broad and structureless feature in this energy region (Figure 1). The main feature is attributed to an IL transition, peaking at 10.375 eV and with a local maximum cross section value of 75.5 Mb. Electron energy loss spectroscopy data reported values at 9.75 eV [6] and 10.3 eV [7], whereas the photoabsorption data of Qi et al. [5] reveals a feature at 10.06 eV followed by a CO vibrational structure with several quanta being excited. Koerting et al. [6] reported that features at 9.8 and 10.4 eV may be due to Rydberg transitions or IL transitions to super-excited states. Several transitions calculated between 10.011 and 10.889 eV with reasonable oscillator strengths may contribute to band V (Table 1). The most intense ones involve the upper 1T1u states of IL or sigma-bond-to-ligand charge transfer (SBLCT) character, whereas 3T1u and 3Eu states may also contribute significantly. In some states the singlet/triplet mixing may be rather important such as in 27T1u and 32T1u for instance.
Conclusion
We have presented a comprehensive investigation of the experimental and theoretical electronic transitions in tungsten hexacarbonyl, W(CO)6. Our high-resolution synchrotron photoabsorption measurements allowed for the identification of previously unresolved experimental features for the first time. The level of accuracy of our relativistic calculations has allowed the reassessment and reassignment of some states, particularly those previously explored below 8 eV. However, despite a reasonable agreement between the TDDFT and VUV absorption spectra we should be aware that the description of double excited states or diffuse Rydberg states is not accessible at the present level of calculation due to the limitation of TDDFT to single excitations. Unfortunately, the use of large diffuse basis sets necessary to correctly describe Rydberg states is beyond the current computational capabilities because of numerical problems due to near-linear dependencies in the basis sets. The combined experimental/theoretical investigation appears relevant to assess the role of W(CO)6 low-lying electronic states that can lead to dissociation. Thus, a reasonable assumption is given that the electronic excitation of tungsten hexacarbonyl leads to direct and statistical bond breaking, the former reminiscent of a repulsive dissociation character by the translational energy distribution of the first CO ligand, the latter correctly modelled by statistical product energy distributions [33].
Supporting Information
| Supporting Information File 1: Additional computational data. | ||
| Format: PDF | Size: 318.0 KB | Download |
Acknowledgements
MM and FFS acknowledge the Portuguese National Funding Agency FCT-MCTES through grants PD/BD/106038/2015 and researcher position IF-FCT IF/00380/2014, respectively, and together with PLV the research grant UID/FIS/00068/2013. KR acknowledges the Swiss National Science Foundation for an Early Postdoc Mobility fellowship. This work was also supported by Radiation Biology and Biophysics Doctoral Training Programme (RaBBiT, PD/00193/2012); UID/Multi/ 04378/2013 (UCIBIO). GG acknowledges partial financial support from the Spanish Ministerio de Economia, Industria y Competitividad (Project No. FIS2016-80440). CD thanks The Labex “Chimie des Systèmes Complexes” (ANR-10-LABX-0026_CSC). The quantum chemical calculations have been performed on the computer nodes of the LCQS, Strasbourg and thanks to the computer facilities of the High Performance Computing (HPC) regional center of University of Strasbourg. The authors wish to acknowledge the beam time at the ASTRID2 synchrotron at ISA, Aarhus University, Denmark. We also acknowledge the financial support provided by the European Community's Seventh Framework Programme (FP7/2007-2013) CALIPSO under grant agreement number 312284. Some of this work forms part of the EU/ESF COST Action CELINA CM1301.
References
-
Gray, H. B.; Beach, N. A. J. Am. Chem. Soc. 1963, 85, 2922–2927. doi:10.1021/ja00902a014
Return to citation in text: [1] [2] [3] [4] [5] -
Beach, N. A.; Gray, H. B. J. Am. Chem. Soc. 1968, 90, 5713–5721. doi:10.1021/ja01023a011
Return to citation in text: [1] [2] [3] [4] [5] -
Iverson, A.; Russell, B. R. Chem. Phys. Lett. 1970, 6, 307–311. doi:10.1016/0009-2614(70)85082-5
Return to citation in text: [1] [2] [3] [4] [5] -
Trogler, W. C.; Desjardins, S. R.; Solomon, E. I. Inorg. Chem. 1979, 18, 2131–2136. doi:10.1021/ic50198a016
Return to citation in text: [1] [2] [3] [4] [5] -
Qi, F.; Yang, X.; Yang, S.; Liu, F.; Sheng, L.; Gao, H.; Zhang, Y.; Yu, S. J. Chem. Phys. 1997, 106, 9474–9482. doi:10.1063/1.474077
Return to citation in text: [1] [2] [3] -
Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] -
Cooper, G.; Sze, K. H.; Brion, C. E. J. Am. Chem. Soc. 1990, 112, 4121–4127. doi:10.1021/ja00167a004
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] -
Pradeep, T. Proc. - Indian Acad. Sci., Chem. Sci. 1990, 102, 1–5.
Return to citation in text: [1] [2] [3] -
Cooper, G.; Green, J. C.; Payne, M. P.; Dobson, B. R.; Hillier, I. H. J. Am. Chem. Soc. 1987, 109, 3836–3843. doi:10.1021/ja00247a003
Return to citation in text: [1] [2] -
Higginson, B. R.; Lloyd, D. R.; Burroughs, P.; Gibson, D. M.; Orchard, A. F. J. Chem. Soc., Faraday Trans. 2 1973, 69, 1659–1668. doi:10.1039/F29736901659
Return to citation in text: [1] -
Lloyd, D. R.; Schlag, E. W. Inorg. Chem. 1969, 8, 2544–2555. doi:10.1021/ic50082a003
Return to citation in text: [1] [2] -
Rolke, J.; Zheng, Y.; Brion, C. E.; Chakravorty, S. J.; Davidson, E. R.; McCarthy, I. E. Chem. Phys. 1997, 215, 191–205. doi:10.1016/S0301-0104(96)00322-9
Return to citation in text: [1] -
Liu, K.; Ning, C. G.; Luo, Z. H.; Shi, L. L.; Deng, J. K. Chem. Phys. Lett. 2010, 497, 229–233. doi:10.1016/j.cplett.2010.08.003
Return to citation in text: [1] -
Yang, C. Y.; Arratia-Perez, R.; Lopez, J. P. Chem. Phys. Lett. 1984, 107, 112–116. doi:10.1016/0009-2614(84)85682-1
Return to citation in text: [1] -
Rosa, A.; Baerends, E. J.; van Gisbergen, S. J. A.; van Lenthe, E.; Groeneveld, J. A.; Snijders, J. G. J. Am. Chem. Soc. 1999, 121, 10356–10365. doi:10.1021/ja990747t
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] [8] -
Hajgató, B.; Morini, F.; Deleuze, M. S. Theor. Chem. Acc. 2012, 131, 1244. doi:10.1007/s00214-012-1244-5
Return to citation in text: [1] -
Ishikawa, Y.; Kawakami, K. J. Phys. Chem. A 2007, 111, 9940–9944. doi:10.1021/jp071509k
Return to citation in text: [1] -
Amster, R. L.; Hannan, R. B.; Tobin, M. C. Spectrochim. Acta 1963, 19, 1489–1494. doi:10.1016/0371-1951(63)80011-9
Return to citation in text: [1] [2] [3] -
Broquier, M.; Crépin, C.; Dubost, H.; Galaup, J.-P. Chem. Phys. 2007, 341, 207–217. doi:10.1016/j.chemphys.2007.06.030
Return to citation in text: [1] [2] -
Jones, L. H. Spectrochim. Acta 1963, 19, 329–338. doi:10.1016/0371-1951(63)80112-5
Return to citation in text: [1] [2] [3] [4] -
van Dorp, W. F.; van Someren, B.; Hagen, C. W.; Kruit, P.; Crozier, P. A. J. Vac. Sci. Technol., B 2006, 24, 618–622. doi:10.1116/1.2170099
Return to citation in text: [1] -
Hoyle, P. C.; Cleaver, J. R. A.; Ahmed, H. J. Vac. Sci. Technol., B 1996, 14, 662–673. doi:10.1116/1.589154
Return to citation in text: [1] -
Rosenberg, S. G.; Barclay, M.; Fairbrother, D. H. Phys. Chem. Chem. Phys. 2013, 15, 4002–4015. doi:10.1039/c3cp43902j
Return to citation in text: [1] -
Muthukumar, K.; Valentí, R.; Jeschke, H. O. J. Chem. Phys. 2014, 140, 184706. doi:10.1063/1.4873584
Return to citation in text: [1] -
Zlatar, M.; Allan, M.; Fedor, J. J. Phys. Chem. C 2016, 120, 10667–10674. doi:10.1021/acs.jpcc.6b02660
Return to citation in text: [1] [2] -
Wnorowski, K.; Stano, M.; Matias, C.; Denifl, S.; Barszczewska, W.; Matejčík, Š. Rapid Commun. Mass Spectrom. 2012, 26, 2093–2098. doi:10.1002/rcm.6324
Return to citation in text: [1] -
Giordan, J. C.; Moore, J. H.; Tossell, J. A. J. Am. Chem. Soc. 1981, 103, 6632–6636. doi:10.1021/ja00412a018
Return to citation in text: [1] [2] -
Wnorowski, K.; Stano, M.; Barszczewska, W.; Jówko, A.; Matejčík, S. Int. J. Mass Spectrom. 2012, 314, 42–48. doi:10.1016/j.ijms.2012.02.002
Return to citation in text: [1] -
Neustetter, M.; Jabbour Al Maalouf, E.; Limão-Vieira, P.; Denifl, S. J. Chem. Phys. 2016, 145, 054301. doi:10.1063/1.4959278
Return to citation in text: [1] -
Neustetter, M.; Mauracher, A.; Limão-Vieira, P.; Denifl, S. Phys. Chem. Chem. Phys. 2016, 18, 9893–9896. doi:10.1039/C6CP00558F
Return to citation in text: [1] -
Eden, S.; Limão-Vieira, P.; Hoffmann, S. V.; Mason, N. J. Chem. Phys. 2006, 323, 313–333. doi:10.1016/j.chemphys.2005.09.040
Return to citation in text: [1] [2] -
Tanaka, H.; Brunger, M. J.; Campbell, L.; Kato, H.; Hoshino, M.; Rau, A. R. P. Rev. Mod. Phys. 2016, 88, 025004. doi:10.1103/RevModPhys.88.025004
Return to citation in text: [1] -
Venkataraman, B.; Hou, H.; Zhang, Z.; Chen, S.; Bandukwalla, G.; Vernon, M. J. Chem. Phys. 1990, 92, 5338–5362. doi:10.1063/1.458513
Return to citation in text: [1] [2] [3] [4] -
Palmer, M. H.; Ridley, T.; Hoffmann, S. V.; Jones, N. C.; Coreno, M.; de Simone, M.; Grazioli, C.; Biczysko, M.; Baiardi, A.; Limão-Vieira, P. J. Chem. Phys. 2015, 142, 134302. doi:10.1063/1.4916121
Return to citation in text: [1] -
Stephens, P. J.; Devlin, F. J.; Chabalowski, C. F.; Frisch, M. J. J. Phys. Chem. 1994, 98, 11623–11627. doi:10.1021/j100096a001
Return to citation in text: [1] -
Van Lenthe, E.; Baerends, E. J. J. Comput. Chem. 2003, 24, 1142–1156. doi:10.1002/jcc.10255
Return to citation in text: [1] -
Berends, T.; Iovkova, L.; Tiekink, E. R. T.; Jurkschat, K. Acta Crystallogr., Sect. E: Struct. Rep. Online 2010, 66, m715–m716. doi:10.1107/S1600536810019343
Return to citation in text: [1] -
van Lenthe, E.; van Leeuwen, R.; Baerends, E. J.; Snijders, J. G. Int. J. Quantum Chem. 1996, 57, 281–293. doi:10.1002/(SICI)1097-461X(1996)57:3<281::AID-QUA2>3.0.CO;2-U
Return to citation in text: [1] -
Runge, E.; Gross, E. K. U. Phys. Rev. Lett. 1984, 52, 997–1000. doi:10.1103/PhysRevLett.52.997
Return to citation in text: [1] -
Petersilka, M.; Gossmann, U.; Gross, E. Phys. Rev. Lett. 1996, 76, 1212–1215. doi:10.1103/PhysRevLett.76.1212
Return to citation in text: [1] -
ADF Modeling Suite - Software for Chemistry & Materials. https://www.scm.com/adf-modeling-suite/ (accessed Sept 28, 2017).
Return to citation in text: [1] -
Fumanal, M.; Daniel, C. J. Comput. Chem. 2016, 37, 2454–2466. doi:10.1002/jcc.24469
Return to citation in text: [1] -
Daniel, C. Top. Curr. Chem. 2016, 368, 377–413. doi:10.1007/128_2015_635
Return to citation in text: [1] -
Daniel, C. Coord. Chem. Rev. 2015, 282–283, 19–32. doi:10.1016/j.ccr.2014.05.023
Return to citation in text: [1] -
Heydová, R.; Gindensperger, E.; Romano, R.; Sýkora, J.; Vlček, A., Jr.; Záliš, S.; Daniel, C. J. Phys. Chem. A 2012, 116, 11319–11329. doi:10.1021/jp305461z
Return to citation in text: [1] -
Baková, R.; Chergui, M.; Daniel, C.; Vlček, A., Jr.; Záliš, S. Coord. Chem. Rev. 2011, 255, 975–989. doi:10.1016/j.ccr.2010.12.027
Return to citation in text: [1] -
Brahim, H.; Daniel, C.; Rahmouni, A. Int. J. Quantum Chem. 2012, 112, 2085–2097. doi:10.1002/qua.23219
Return to citation in text: [1] -
Záliš, S.; Ben Amor, N.; Daniel, C. Inorg. Chem. 2004, 43, 7978–7985. doi:10.1021/ic049464e
Return to citation in text: [1] -
Ben Amor, N.; Villaume, S.; Maynau, D.; Daniel, C. Chem. Phys. Lett. 2006, 421, 378–382. doi:10.1016/j.cplett.2006.02.002
Return to citation in text: [1] -
Nobre, M.; Fernandes, A.; Ferreira da Silva, F.; Antunes, R.; Almeida, D.; Kokhan, V.; Hoffmann, S. V.; Mason, N. J.; Eden, S.; Limão-Vieira, P. Phys. Chem. Chem. Phys. 2008, 10, 550–560. doi:10.1039/B708580J
Return to citation in text: [1] -
Jones, D. B.; Limão-Vieira, P.; Mendes, M.; Jones, N. C.; Hoffmann, S. V.; da Costa, R. F.; do N. Varella, M. T. N.; Bettega, M. H. F.; Blanco, F.; Garcia, G.; Ingolfsson, O.; Lima, M. A. P.; Brunger, M. J. J. Chem. Phys. 2017, 146, 184303. doi:10.1063/1.4982940
Return to citation in text: [1]
| 34. | Palmer, M. H.; Ridley, T.; Hoffmann, S. V.; Jones, N. C.; Coreno, M.; de Simone, M.; Grazioli, C.; Biczysko, M.; Baiardi, A.; Limão-Vieira, P. J. Chem. Phys. 2015, 142, 134302. doi:10.1063/1.4916121 |
| 35. | Stephens, P. J.; Devlin, F. J.; Chabalowski, C. F.; Frisch, M. J. J. Phys. Chem. 1994, 98, 11623–11627. doi:10.1021/j100096a001 |
| 50. | Nobre, M.; Fernandes, A.; Ferreira da Silva, F.; Antunes, R.; Almeida, D.; Kokhan, V.; Hoffmann, S. V.; Mason, N. J.; Eden, S.; Limão-Vieira, P. Phys. Chem. Chem. Phys. 2008, 10, 550–560. doi:10.1039/B708580J |
| 51. | Jones, D. B.; Limão-Vieira, P.; Mendes, M.; Jones, N. C.; Hoffmann, S. V.; da Costa, R. F.; do N. Varella, M. T. N.; Bettega, M. H. F.; Blanco, F.; Garcia, G.; Ingolfsson, O.; Lima, M. A. P.; Brunger, M. J. J. Chem. Phys. 2017, 146, 184303. doi:10.1063/1.4982940 |
| 36. | Van Lenthe, E.; Baerends, E. J. J. Comput. Chem. 2003, 24, 1142–1156. doi:10.1002/jcc.10255 |
| 15. | Rosa, A.; Baerends, E. J.; van Gisbergen, S. J. A.; van Lenthe, E.; Groeneveld, J. A.; Snijders, J. G. J. Am. Chem. Soc. 1999, 121, 10356–10365. doi:10.1021/ja990747t |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
| 7. | Cooper, G.; Sze, K. H.; Brion, C. E. J. Am. Chem. Soc. 1990, 112, 4121–4127. doi:10.1021/ja00167a004 |
| 3. | Iverson, A.; Russell, B. R. Chem. Phys. Lett. 1970, 6, 307–311. doi:10.1016/0009-2614(70)85082-5 |
| 18. | Amster, R. L.; Hannan, R. B.; Tobin, M. C. Spectrochim. Acta 1963, 19, 1489–1494. doi:10.1016/0371-1951(63)80011-9 |
| 19. | Broquier, M.; Crépin, C.; Dubost, H.; Galaup, J.-P. Chem. Phys. 2007, 341, 207–217. doi:10.1016/j.chemphys.2007.06.030 |
| 41. | ADF Modeling Suite - Software for Chemistry & Materials. https://www.scm.com/adf-modeling-suite/ (accessed Sept 28, 2017). |
| 11. | Lloyd, D. R.; Schlag, E. W. Inorg. Chem. 1969, 8, 2544–2555. doi:10.1021/ic50082a003 |
| 42. | Fumanal, M.; Daniel, C. J. Comput. Chem. 2016, 37, 2454–2466. doi:10.1002/jcc.24469 |
| 43. | Daniel, C. Top. Curr. Chem. 2016, 368, 377–413. doi:10.1007/128_2015_635 |
| 44. | Daniel, C. Coord. Chem. Rev. 2015, 282–283, 19–32. doi:10.1016/j.ccr.2014.05.023 |
| 45. | Heydová, R.; Gindensperger, E.; Romano, R.; Sýkora, J.; Vlček, A., Jr.; Záliš, S.; Daniel, C. J. Phys. Chem. A 2012, 116, 11319–11329. doi:10.1021/jp305461z |
| 46. | Baková, R.; Chergui, M.; Daniel, C.; Vlček, A., Jr.; Záliš, S. Coord. Chem. Rev. 2011, 255, 975–989. doi:10.1016/j.ccr.2010.12.027 |
| 47. | Brahim, H.; Daniel, C.; Rahmouni, A. Int. J. Quantum Chem. 2012, 112, 2085–2097. doi:10.1002/qua.23219 |
| 48. | Záliš, S.; Ben Amor, N.; Daniel, C. Inorg. Chem. 2004, 43, 7978–7985. doi:10.1021/ic049464e |
| 38. | van Lenthe, E.; van Leeuwen, R.; Baerends, E. J.; Snijders, J. G. Int. J. Quantum Chem. 1996, 57, 281–293. doi:10.1002/(SICI)1097-461X(1996)57:3<281::AID-QUA2>3.0.CO;2-U |
| 7. | Cooper, G.; Sze, K. H.; Brion, C. E. J. Am. Chem. Soc. 1990, 112, 4121–4127. doi:10.1021/ja00167a004 |
| 39. | Runge, E.; Gross, E. K. U. Phys. Rev. Lett. 1984, 52, 997–1000. doi:10.1103/PhysRevLett.52.997 |
| 40. | Petersilka, M.; Gossmann, U.; Gross, E. Phys. Rev. Lett. 1996, 76, 1212–1215. doi:10.1103/PhysRevLett.76.1212 |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
| 7. | Cooper, G.; Sze, K. H.; Brion, C. E. J. Am. Chem. Soc. 1990, 112, 4121–4127. doi:10.1021/ja00167a004 |
| 15. | Rosa, A.; Baerends, E. J.; van Gisbergen, S. J. A.; van Lenthe, E.; Groeneveld, J. A.; Snijders, J. G. J. Am. Chem. Soc. 1999, 121, 10356–10365. doi:10.1021/ja990747t |
| 3. | Iverson, A.; Russell, B. R. Chem. Phys. Lett. 1970, 6, 307–311. doi:10.1016/0009-2614(70)85082-5 |
| 37. | Berends, T.; Iovkova, L.; Tiekink, E. R. T.; Jurkschat, K. Acta Crystallogr., Sect. E: Struct. Rep. Online 2010, 66, m715–m716. doi:10.1107/S1600536810019343 |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
| 20. | Jones, L. H. Spectrochim. Acta 1963, 19, 329–338. doi:10.1016/0371-1951(63)80112-5 |
| 2. | Beach, N. A.; Gray, H. B. J. Am. Chem. Soc. 1968, 90, 5713–5721. doi:10.1021/ja01023a011 |
| 33. | Venkataraman, B.; Hou, H.; Zhang, Z.; Chen, S.; Bandukwalla, G.; Vernon, M. J. Chem. Phys. 1990, 92, 5338–5362. doi:10.1063/1.458513 |
| 49. | Ben Amor, N.; Villaume, S.; Maynau, D.; Daniel, C. Chem. Phys. Lett. 2006, 421, 378–382. doi:10.1016/j.cplett.2006.02.002 |
| 5. | Qi, F.; Yang, X.; Yang, S.; Liu, F.; Sheng, L.; Gao, H.; Zhang, Y.; Yu, S. J. Chem. Phys. 1997, 106, 9474–9482. doi:10.1063/1.474077 |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
| 7. | Cooper, G.; Sze, K. H.; Brion, C. E. J. Am. Chem. Soc. 1990, 112, 4121–4127. doi:10.1021/ja00167a004 |
| 4. | Trogler, W. C.; Desjardins, S. R.; Solomon, E. I. Inorg. Chem. 1979, 18, 2131–2136. doi:10.1021/ic50198a016 |
| 15. | Rosa, A.; Baerends, E. J.; van Gisbergen, S. J. A.; van Lenthe, E.; Groeneveld, J. A.; Snijders, J. G. J. Am. Chem. Soc. 1999, 121, 10356–10365. doi:10.1021/ja990747t |
| 7. | Cooper, G.; Sze, K. H.; Brion, C. E. J. Am. Chem. Soc. 1990, 112, 4121–4127. doi:10.1021/ja00167a004 |
| 1. | Gray, H. B.; Beach, N. A. J. Am. Chem. Soc. 1963, 85, 2922–2927. doi:10.1021/ja00902a014 |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
| 15. | Rosa, A.; Baerends, E. J.; van Gisbergen, S. J. A.; van Lenthe, E.; Groeneveld, J. A.; Snijders, J. G. J. Am. Chem. Soc. 1999, 121, 10356–10365. doi:10.1021/ja990747t |
| 4. | Trogler, W. C.; Desjardins, S. R.; Solomon, E. I. Inorg. Chem. 1979, 18, 2131–2136. doi:10.1021/ic50198a016 |
| 1. | Gray, H. B.; Beach, N. A. J. Am. Chem. Soc. 1963, 85, 2922–2927. doi:10.1021/ja00902a014 |
| 2. | Beach, N. A.; Gray, H. B. J. Am. Chem. Soc. 1968, 90, 5713–5721. doi:10.1021/ja01023a011 |
| 27. | Giordan, J. C.; Moore, J. H.; Tossell, J. A. J. Am. Chem. Soc. 1981, 103, 6632–6636. doi:10.1021/ja00412a018 |
| 1. | Gray, H. B.; Beach, N. A. J. Am. Chem. Soc. 1963, 85, 2922–2927. doi:10.1021/ja00902a014 |
| 2. | Beach, N. A.; Gray, H. B. J. Am. Chem. Soc. 1968, 90, 5713–5721. doi:10.1021/ja01023a011 |
| 3. | Iverson, A.; Russell, B. R. Chem. Phys. Lett. 1970, 6, 307–311. doi:10.1016/0009-2614(70)85082-5 |
| 4. | Trogler, W. C.; Desjardins, S. R.; Solomon, E. I. Inorg. Chem. 1979, 18, 2131–2136. doi:10.1021/ic50198a016 |
| 5. | Qi, F.; Yang, X.; Yang, S.; Liu, F.; Sheng, L.; Gao, H.; Zhang, Y.; Yu, S. J. Chem. Phys. 1997, 106, 9474–9482. doi:10.1063/1.474077 |
| 12. | Rolke, J.; Zheng, Y.; Brion, C. E.; Chakravorty, S. J.; Davidson, E. R.; McCarthy, I. E. Chem. Phys. 1997, 215, 191–205. doi:10.1016/S0301-0104(96)00322-9 |
| 13. | Liu, K.; Ning, C. G.; Luo, Z. H.; Shi, L. L.; Deng, J. K. Chem. Phys. Lett. 2010, 497, 229–233. doi:10.1016/j.cplett.2010.08.003 |
| 24. | Muthukumar, K.; Valentí, R.; Jeschke, H. O. J. Chem. Phys. 2014, 140, 184706. doi:10.1063/1.4873584 |
| 7. | Cooper, G.; Sze, K. H.; Brion, C. E. J. Am. Chem. Soc. 1990, 112, 4121–4127. doi:10.1021/ja00167a004 |
| 11. | Lloyd, D. R.; Schlag, E. W. Inorg. Chem. 1969, 8, 2544–2555. doi:10.1021/ic50082a003 |
| 25. | Zlatar, M.; Allan, M.; Fedor, J. J. Phys. Chem. C 2016, 120, 10667–10674. doi:10.1021/acs.jpcc.6b02660 |
| 9. | Cooper, G.; Green, J. C.; Payne, M. P.; Dobson, B. R.; Hillier, I. H. J. Am. Chem. Soc. 1987, 109, 3836–3843. doi:10.1021/ja00247a003 |
| 10. | Higginson, B. R.; Lloyd, D. R.; Burroughs, P.; Gibson, D. M.; Orchard, A. F. J. Chem. Soc., Faraday Trans. 2 1973, 69, 1659–1668. doi:10.1039/F29736901659 |
| 21. | van Dorp, W. F.; van Someren, B.; Hagen, C. W.; Kruit, P.; Crozier, P. A. J. Vac. Sci. Technol., B 2006, 24, 618–622. doi:10.1116/1.2170099 |
| 22. | Hoyle, P. C.; Cleaver, J. R. A.; Ahmed, H. J. Vac. Sci. Technol., B 1996, 14, 662–673. doi:10.1116/1.589154 |
| 4. | Trogler, W. C.; Desjardins, S. R.; Solomon, E. I. Inorg. Chem. 1979, 18, 2131–2136. doi:10.1021/ic50198a016 |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
| 7. | Cooper, G.; Sze, K. H.; Brion, C. E. J. Am. Chem. Soc. 1990, 112, 4121–4127. doi:10.1021/ja00167a004 |
| 8. | Pradeep, T. Proc. - Indian Acad. Sci., Chem. Sci. 1990, 102, 1–5. |
| 23. | Rosenberg, S. G.; Barclay, M.; Fairbrother, D. H. Phys. Chem. Chem. Phys. 2013, 15, 4002–4015. doi:10.1039/c3cp43902j |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
| 16. | Hajgató, B.; Morini, F.; Deleuze, M. S. Theor. Chem. Acc. 2012, 131, 1244. doi:10.1007/s00214-012-1244-5 |
| 18. | Amster, R. L.; Hannan, R. B.; Tobin, M. C. Spectrochim. Acta 1963, 19, 1489–1494. doi:10.1016/0371-1951(63)80011-9 |
| 1. | Gray, H. B.; Beach, N. A. J. Am. Chem. Soc. 1963, 85, 2922–2927. doi:10.1021/ja00902a014 |
| 2. | Beach, N. A.; Gray, H. B. J. Am. Chem. Soc. 1968, 90, 5713–5721. doi:10.1021/ja01023a011 |
| 15. | Rosa, A.; Baerends, E. J.; van Gisbergen, S. J. A.; van Lenthe, E.; Groeneveld, J. A.; Snijders, J. G. J. Am. Chem. Soc. 1999, 121, 10356–10365. doi:10.1021/ja990747t |
| 18. | Amster, R. L.; Hannan, R. B.; Tobin, M. C. Spectrochim. Acta 1963, 19, 1489–1494. doi:10.1016/0371-1951(63)80011-9 |
| 19. | Broquier, M.; Crépin, C.; Dubost, H.; Galaup, J.-P. Chem. Phys. 2007, 341, 207–217. doi:10.1016/j.chemphys.2007.06.030 |
| 20. | Jones, L. H. Spectrochim. Acta 1963, 19, 329–338. doi:10.1016/0371-1951(63)80112-5 |
| 3. | Iverson, A.; Russell, B. R. Chem. Phys. Lett. 1970, 6, 307–311. doi:10.1016/0009-2614(70)85082-5 |
| 2. | Beach, N. A.; Gray, H. B. J. Am. Chem. Soc. 1968, 90, 5713–5721. doi:10.1021/ja01023a011 |
| 15. | Rosa, A.; Baerends, E. J.; van Gisbergen, S. J. A.; van Lenthe, E.; Groeneveld, J. A.; Snijders, J. G. J. Am. Chem. Soc. 1999, 121, 10356–10365. doi:10.1021/ja990747t |
| 14. | Yang, C. Y.; Arratia-Perez, R.; Lopez, J. P. Chem. Phys. Lett. 1984, 107, 112–116. doi:10.1016/0009-2614(84)85682-1 |
| 17. | Ishikawa, Y.; Kawakami, K. J. Phys. Chem. A 2007, 111, 9940–9944. doi:10.1021/jp071509k |
| 20. | Jones, L. H. Spectrochim. Acta 1963, 19, 329–338. doi:10.1016/0371-1951(63)80112-5 |
| 28. | Wnorowski, K.; Stano, M.; Barszczewska, W.; Jówko, A.; Matejčík, S. Int. J. Mass Spectrom. 2012, 314, 42–48. doi:10.1016/j.ijms.2012.02.002 |
| 26. | Wnorowski, K.; Stano, M.; Matias, C.; Denifl, S.; Barszczewska, W.; Matejčík, Š. Rapid Commun. Mass Spectrom. 2012, 26, 2093–2098. doi:10.1002/rcm.6324 |
| 27. | Giordan, J. C.; Moore, J. H.; Tossell, J. A. J. Am. Chem. Soc. 1981, 103, 6632–6636. doi:10.1021/ja00412a018 |
| 3. | Iverson, A.; Russell, B. R. Chem. Phys. Lett. 1970, 6, 307–311. doi:10.1016/0009-2614(70)85082-5 |
| 4. | Trogler, W. C.; Desjardins, S. R.; Solomon, E. I. Inorg. Chem. 1979, 18, 2131–2136. doi:10.1021/ic50198a016 |
| 20. | Jones, L. H. Spectrochim. Acta 1963, 19, 329–338. doi:10.1016/0371-1951(63)80112-5 |
| 15. | Rosa, A.; Baerends, E. J.; van Gisbergen, S. J. A.; van Lenthe, E.; Groeneveld, J. A.; Snijders, J. G. J. Am. Chem. Soc. 1999, 121, 10356–10365. doi:10.1021/ja990747t |
| 33. | Venkataraman, B.; Hou, H.; Zhang, Z.; Chen, S.; Bandukwalla, G.; Vernon, M. J. Chem. Phys. 1990, 92, 5338–5362. doi:10.1063/1.458513 |
| 31. | Eden, S.; Limão-Vieira, P.; Hoffmann, S. V.; Mason, N. J. Chem. Phys. 2006, 323, 313–333. doi:10.1016/j.chemphys.2005.09.040 |
| 32. | Tanaka, H.; Brunger, M. J.; Campbell, L.; Kato, H.; Hoshino, M.; Rau, A. R. P. Rev. Mod. Phys. 2016, 88, 025004. doi:10.1103/RevModPhys.88.025004 |
| 33. | Venkataraman, B.; Hou, H.; Zhang, Z.; Chen, S.; Bandukwalla, G.; Vernon, M. J. Chem. Phys. 1990, 92, 5338–5362. doi:10.1063/1.458513 |
| 5. | Qi, F.; Yang, X.; Yang, S.; Liu, F.; Sheng, L.; Gao, H.; Zhang, Y.; Yu, S. J. Chem. Phys. 1997, 106, 9474–9482. doi:10.1063/1.474077 |
| 33. | Venkataraman, B.; Hou, H.; Zhang, Z.; Chen, S.; Bandukwalla, G.; Vernon, M. J. Chem. Phys. 1990, 92, 5338–5362. doi:10.1063/1.458513 |
| 25. | Zlatar, M.; Allan, M.; Fedor, J. J. Phys. Chem. C 2016, 120, 10667–10674. doi:10.1021/acs.jpcc.6b02660 |
| 9. | Cooper, G.; Green, J. C.; Payne, M. P.; Dobson, B. R.; Hillier, I. H. J. Am. Chem. Soc. 1987, 109, 3836–3843. doi:10.1021/ja00247a003 |
| 31. | Eden, S.; Limão-Vieira, P.; Hoffmann, S. V.; Mason, N. J. Chem. Phys. 2006, 323, 313–333. doi:10.1016/j.chemphys.2005.09.040 |
| 15. | Rosa, A.; Baerends, E. J.; van Gisbergen, S. J. A.; van Lenthe, E.; Groeneveld, J. A.; Snijders, J. G. J. Am. Chem. Soc. 1999, 121, 10356–10365. doi:10.1021/ja990747t |
| 29. | Neustetter, M.; Jabbour Al Maalouf, E.; Limão-Vieira, P.; Denifl, S. J. Chem. Phys. 2016, 145, 054301. doi:10.1063/1.4959278 |
| 1. | Gray, H. B.; Beach, N. A. J. Am. Chem. Soc. 1963, 85, 2922–2927. doi:10.1021/ja00902a014 |
| 30. | Neustetter, M.; Mauracher, A.; Limão-Vieira, P.; Denifl, S. Phys. Chem. Chem. Phys. 2016, 18, 9893–9896. doi:10.1039/C6CP00558F |
| 6. | Koerting, C. F.; Walzl, K. N.; Kuppermann, A. J. Chem. Phys. 1987, 86, 6646–6653. doi:10.1063/1.452411 |
© 2017 Mendes et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Nanotechnology terms and conditions: (http://www.beilstein-journals.org/bjnano)