Abstract
We report on experimental studies focusing on the dynamic ac magnetic susceptibility of a ferronematic. It has been shown recently, that in the isotropic phase of a ferronematic, a weak dc bias magnetic field of a few oersteds increases the ac magnetic susceptibility. This increment vanishes irreversibly if the substance is cooled down to the nematic phase, but can be reinduced by applying the dc bias field again in the isotropic phase [Tomašovičová, N. et al. Soft Matter 2016, 12, 5780–5786]. The effect has no analogue in the neat host liquid crystal. Here, we demonstrate that by doubling the concentration of the magnetic nanoparticles, the range of the dc bias magnetic field to which the ferronematic is sensitive without saturation can be increased by about two orders of magnitude. This finding paves a way to application possibilities, such as low magnetic field sensors, or basic logical elements for information storage.
Introduction
The great attention that nematic liquid crystals (LCs) have attracted in recent decades is due to the anisotropy of their physical properties. This anisotropy allows for a realignment of their director (the axis of cylindrical symmetry) by external electrical or magnetic fields, or by shear [1]. In common nematics, the threshold voltage of the reorientational response is just a few volts, owing to the relatively large anisotropy of the dielectric permittivity. Analogous effects exist with magnetic fields. However, the threshold magnetic fields are high (B = μ0H ≈ 1 T) as a consequence of the small diamagnetic susceptibility anisotropy (χa ≈ 10−6) of liquid crystals. As a way of lowering the required applied magnetic field, doping liquid crystals with magnetic nanoparticles (MNPs) has been proposed [2]. The stable colloidal suspensions of MNPs in nematic LCs are now known as ferronematics (FNs). Following the first implementation of ferronematics [3], they soon have become favourite targets for research. Several theoretical models have been developed by extending the Ericksen–Leslie continuum theory [4-6], or the hydrodynamic description [1,7,8] for taking into account the interactions between MNPs, the host liquid crystal and the magnetic field. Experiments have proved that MNPs can alter the threshold fields for structural (e.g., Fréedericksz) transitions [9-11]; unexpected magneto-optical [12,13] and magneto-dielectric effects [14] have been found and shifts in the isotropic-to-nematic phase-transition temperature with and without magnetic field have been demonstrated [15-17]. For the interpretation of the latter effect mean-field theoretical models have been developed [18,19]. These studies have proven that doping modifies the material properties of the host liquid crystal. The improvement of certain properties, such as the capability of these materials to respond to external magnetic field more efficiently, comes from the collective properties of the MNPs dispersed in the liquid crystal. In this respect, investigation of such colloidal LC systems opens up new perspectives even for applications.
While the consequences of the behavior of FNs in static magnetic fields have been studied widely, much less is known about their dynamic properties. Theoretical calculations have been performed for various geometries to uncover how the magnetic field affects the flow properties of FNs [1,20], the pattern forming instabilities in FNs [8] or the behavior in rotating magnetic fields [21-25]. Experimental studies on dynamics are very scarce [26], thus most theoretical predictions still await experimental justification. In a recent work [27], we investigated the response of FNs to a small alternating magnetic field, measuring the ac magnetic susceptibility. We found that, unexpectedly, a small bias magnetic field (Hdc above ca. 10 Oe) applied to the ferronematic in the isotropic phase increased its ac susceptibility by about 10%. This increment vanished irreversibly at passing the isotropic-to-nematic phase transition on cooling (unless the bias field is applied again in the isotropic phase). A phenomenological explanation of the experimental results related this behavior to defect-mediated aggregation and magnetic-field-assisted disaggregation of MNPs [27].
In principle, the effect can provide a concept for potential future applications as sensors, or logical gates in micro- and nanodevices. However, the ferronematic composition investigated in [27] turned out to be sensitive to Hdc > 8 Oe only. Moreover, the effect of the increase in the ac susceptibility saturated for Hdc > 10 Oe. Therefore, the ferronematic composition reported in [27] can serve as a logical gate with a “yes” or “no” response to a prior existence of the biasing magnetic field Hdc > 8 Oe, rather than to function as a sensor that can sense and measure the magnitude of Hdc.
The present work aims at the optimization of the ferronematic composition for sensor applications, through broadening the range of the magnetic field to which the suspension is sensitive without saturation.
Experimental
Measurements were performed in a FN sample based on the calamitic thermotropic liquid crystal 4-n-hexyl-4'-cyanobiphenyl (6CB) [28,29]. This liquid-crystalline matrix was doped with spherical magnetic particles purchased from Ocean NanoTech. The mean diameter of the Fe3O4 magnetic particles was d = 20 nm. They were coated with oleic acid and dissolved in chloroform. This suspension was admixed to the liquid crystal, and the solvent was let to evaporate. The final volume concentration of the solid particles was = 2 × 10−4, i.e., two times larger than in the FN investigated recently [27].
For magnetic measurements the sample was filled into cylindrical capsules of 2.5 mm in diameter and 6.5 mm in length. The magnetic properties were measured with a SQUID magnetometer (Quantum Design MPMS 5XL) [30] in a magnetic field directed along the cylindrical axis of the capsules. Figure 1 shows the magnetization curve of the powder of MNPs obtained by evaporating the chloroform, measured at 285 K. This figure proves that the particles are superparamagnetic.
![[2190-4286-8-251-1]](/bjnano/content/figures/2190-4286-8-251-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: Magnetization curve of the powder of Fe3O4 magnetic nanoparticles, measured at 285 K.
Figure 1: Magnetization curve of the powder of Fe3O4 magnetic nanoparticles, measured at 285 K.
The temperature of the phase transition of the samples was detected by independent capacitance measurements in a capacitor made of ITO-coated glass electrodes (AWAT). The capacitor with an electrode area of approximately 5 mm × 5 mm was placed into a regulated thermostat system; the temperature was stabilized with an accuracy of 0.05 °C. The distance between the electrodes (sample thickness) was D = 5 μm. The capacitance was measured at a frequency of 1 kHz with an Andeen Hagerling high-precision capacitance bridge. The samples were first heated to the isotropic phase; then the measurement was carried out while cooling with a rate of 1 °C/min.
Results and Discussion
The temperature TIN of the phase transition from isotropic (I) to nematic (N) was determined by capacitance measurements presented in Figure 2. TIN of neat 6CB is 302 K, while doping with the MNPs shifted the phase transition temperature to a lower value of TIN ≈ 300 K. This shift in TIN is slightly larger than that obtained at the lower dopant concentration of = 10−4 [27]).
![[2190-4286-8-251-2]](/bjnano/content/figures/2190-4286-8-251-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2:
Temperature dependence of the capacitance of 6CB and of two ferronematic samples with different MNP concentrations, .
Figure 2: Temperature dependence of the capacitance of 6CB and of two ferronematic samples with different MNP...
Figure 3 shows the magnetization curves of neat 6CB and of the two 6CB-based ferronematics ( = 10−4 and
= 2 × 10−4), measured in the nematic phase, and that of the 6CB-based FN with a MNP concentration of
= 2 × 10−4, measured in the isotropic phase (T = 315 K). The straight line for 6CB indicates the usual diamagnetic behavior. In contrast to that, at low magnetic fields the FN composites are superparamagnets; they exhibit no hysteresis. At higher magnetic fields (H > 3000 Oe), diamagnetism of the host LC matrix becomes dominating. The distances between the magnetization curves with negative slope of 6CB and of the FNs at these high magnetic fields correspond to the saturation magnetization of the MNPs. For higher concentration of MNPs this distance is larger, as expected. No significant difference is found between the behavior in the isotropic and in the nematic phase, implying that the type of the fluid phase of the FN does not affect the quasi-static magnetic properties.
![[2190-4286-8-251-3]](/bjnano/content/figures/2190-4286-8-251-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3:
Magnetization curves of neat 6CB and the FN with a MNP concentration of = 10−4 in the nematic phase, as well as of the FN with a higher concentration of MNPs (
= 2 × 10−4 ) in the nematic (285 K) and isotropic (315 K) phases.
Figure 3:
Magnetization curves of neat 6CB and the FN with a MNP concentration of = 10−4 in the nematic phas...
The ac magnetic susceptibility, χ, of the prepared sample was measured in the same experimental geometry as the magnetization curves. An ac magnetic field of 1 Oe was applied at a frequency of f = 10 Hz. To measure the temperature dependence of χ, the sample was first heated to 315 K (isotropic phase), then slowly cooled down to the nematic phase and finally slowly heated up again to 315 K. The ac susceptibility was measured at a sequence of temperatures (with a temperature step size of 1 K). At each temperature the sample was thermally stabilized for 3 min before determining χ. Then the next temperature was achieved with a heating/cooling rate of 0.5 K/min. Before each cooling–heating cycle, first a dc magnetic field Hdc was applied in the isotropic phase typically for 10 min, then it was switched off. This is the same protocol as that used in [27].
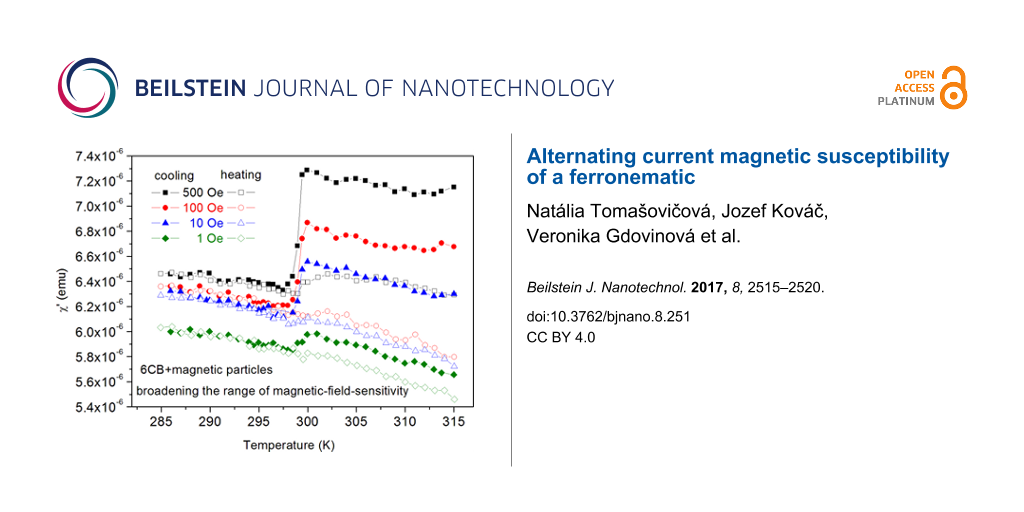
Figure 4 presents the real part χ′ of the ac magnetic susceptibility as a function of temperature for different Hdc ranging from 1 to 2000 Oe, during cooling (solid symbols) as well as during heating (open symbols). It can be seen that χ′(T) has a negative slope in the isotropic, as well as in the nematic phase, except in a very narrow temperature range during cooling, where χ′ undergoes a sudden reduction of up to about 10%. Passing the same temperature range in heating, typically, does not affect χ′. It changes monotonically without any jump. The temperature range where the jump in χ′ occurs on cooling corresponds to the temperature of the isotropic-to-nematic phase transition TIN, cf. Figure 4 and Figure 2.
![[2190-4286-8-251-4]](/bjnano/content/figures/2190-4286-8-251-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: Temperature dependence of the real part χ′ of the ac susceptibility of the 6CB-based FN, measured in a cooling–heating cycle, after applying and switching off a dc magnetic field Hdc of (a) 1–6 Oe, (b) 7–100 Oe and (c) 100–2000 Oe. Solid symbols stand for cooling, while open symbols stand for heating.
Figure 4: Temperature dependence of the real part χ′ of the ac susceptibility of the 6CB-based FN, measured i...
Figure 4 clearly shows that the ac magnetic susceptibility of the FN is a two-valued function of the temperature in the isotropic phase. The lower value belongs to the ferronematic, which has not yet been subjected to a dc magnetic field after heating up to the isotropic phase. The other (higher) value is induced by the application of a relatively small dc magnetic field Hdc. The magnitude Δχ′ of the sudden reduction in χ′ depends on Hdc, as shown in Figure 5. It saturates at approximately 500 Oe.
![[2190-4286-8-251-5]](/bjnano/content/figures/2190-4286-8-251-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: Magnitude of the reduction in the ac susceptibility Δχ′ at the isotropic-to-nematic phase transition as a function of the dc bias magnetic field.
Figure 5: Magnitude of the reduction in the ac susceptibility Δχ′ at the isotropic-to-nematic phase transitio...
The increment Δχ′ is evidently due to the presence of magnetic nanoparticles, since this effect is completely absent in the neat liquid crystal [27]. According to our model [27], Hdc aligns the magnetic moments of nanoparticle aggregates, forcing them into a state with inconveniently high energy, thus promoting the breakaway of single particles from the aggregates. This increases the number of particles capable for magnetic reorientation by the ac testing magnetic field (large aggregates practically do not contribute to χ′). These changes in the particle distribution persist in the isotropic phase, but are annulled at entering into the nematic phase, since the disclinations emerging at the isotropic-to-nematic phase transition strongly promote particle aggregation.
Analyzing the above presented results, and comparing them with those reported in [27] for the FN with a lower concentration of MNPs, several conclusions can be drawn:
(i.) Most importantly, the range of the bias magnetic field to which the FN is sensitive without saturation has increased by about two orders of magnitude with the increase of the concentration of MNPs, . Namely, for
= 10−4 this range was found between 8 Oe < Hdc ≤ 10 Oe [27], while for
= 2 × 10 −4 it is 1 Oe ≤ Hdc ≤ 500 Oe (Figure 5).
(ii.) The highest achievable relative magnitude Δχ′/χ′ of the sudden drop in the ac susceptibility at TIN seems to be independent of the concentration of MNPs: It is about 10% for both = 10−4 [27] and
= 2 × 10−4. At higher Hdc the effect saturates for both concentrations, and the relative magnitude of the drop remains the same. It is a question for future research whether this holds for FNs of different compositions (different host LC and/or different MNPs).
(iii.) For the higher concentration of MNPs a higher value of ac susceptibility χ′ is observed (cf. Figure 4 and Figure 4 of [27]), which is in line with our phenomenological model: The higher concentration of MNPs results in a larger number of individual particles and dimers that contribute to the ac susceptibility. Nevertheless, the effect is not linear; multiparticle aggregates with nearly closed flux virtually do not contribute to χ′ and at the higher concentration there is an enhanced tendency for the formation of such aggregates.
(iv.) The value of the ac susceptibility in Figure 4 is temperature-dependent, while no such dependence was found for the lower concentration of = 10−4 (see Figures 3–5 of [27]). The fact the χ′ is independent of the temperature at the lower concentration is surprising. Namely, although diamagnetism is temperature-independent in the temperature range of our measurements, ferromagnetism decreases with temperature as T−3/2. The decrease in spontaneous magnetization at higher temperatures is caused by the increased excitation of spin waves. The decrease of the ac susceptibility with the temperature is related to the decrease of magnetization. Therefore, the absence of a temperature dependence of χ′ at the lower concentration of MNPs [27] is a strong indication of the absence of interaction between MNPs.
(v.) The value of the ac susceptibility in the nematic phase, as well as in the isotropic phase during heating, slightly increases with the increase of Hdc (this effect was again unnoticed at the lower concentration of MNPs [27]). This behavior indicates that a larger Hdc has a slightly higher disaggregation capability, i.e., it produces a slightly larger number of single MNPs or dimers contributing to χ′(T), and some of them remain nonaggregated above the isotropic-to-nematic phase transition temperature.
(vi.) In addition to the bias-field-dependent shift of the χ′(T) curve mentioned above, for Hdc ≥ 500 Oe, where the magnitude of the sudden drop Δχ′ saturates, the value of χ′ slightly increases during heating at the nematic-to-isotropic phase transition temperature. This effect is still not fully understood, and will be a subject for future studies, together with the more detailed analysis of the processes leading to the saturation of Δχ′ (Figure 5).
In summary, we have shown experimentally that the sensitivity range of FNs to magnetic fields can be extended significantly by the optimization of the FN composition, and that, in principle, the effect may be used for sensing low magnetic fields.
References
-
Jarkova, E.; Pleiner, H.; Müller, H.-W.; Brand, H. R. J. Chem. Phys. 2003, 118, 2422–2430. doi:10.1063/1.1533788
Return to citation in text: [1] [2] [3] -
Brochard, F.; de Gennes, P. G. J. Phys. (Paris) 1970, 31, 691–708. doi:10.1051/jphys:01970003107069100
Return to citation in text: [1] -
Chen, S.-H.; Amer, N. M. Phys. Rev. Lett. 1983, 51, 2298–2301. doi:10.1103/PhysRevLett.51.2298
Return to citation in text: [1] -
Burylov, S. V.; Raikher, Y. L. Mater. Sci. Eng., C 1995, 2, 235–241. doi:10.1016/0928-4931(95)00093-3
Return to citation in text: [1] -
Burylov, S. V.; Raikher, Y. L. Mol. Cryst. Liq. Cryst. 1995, 258, 107–122. doi:10.1080/10587259508034552
Return to citation in text: [1] -
Zakhlevnykh, A. N.; Petrov, D. A. J. Magn. Magn. Mater. 2016, 401, 188–195. doi:10.1016/j.jmmm.2015.10.025
Return to citation in text: [1] -
Jarkova, E.; Pleiner, H.; Müller, H.-W.; Fink, A.; Brand, H. R. Eur. Phys. J. E 2001, 5, 583–588. doi:10.1007/s101890170041
Return to citation in text: [1] -
Ryskin, A. B.; Pleiner, H.; Müller, H. W. Eur. Phys. J. E 2003, 11, 389–397. doi:10.1140/epje/i2003-10047-1
Return to citation in text: [1] [2] -
Tomašovičová, N.; Koneracká, M.; Kopčanský, P.; Timko, M.; Závišová, V.; Jadzyn, J. Phase Transitions 2006, 79, 595–603. doi:10.1080/01411590600892633
Return to citation in text: [1] -
Kopčanský, P.; Tomašovičová, N.; Koneracká, M.; Závišová, V.; Timko, M.; Džarová, A.; Šprincová, A.; Éber, N.; Fodor-Csorba, K.; Tóth-Katona, T.; Vajda, A.; Jadzyn, J. Phys. Rev. E 2008, 78, 011702. doi:10.1103/PhysRevE.78.011702
Return to citation in text: [1] -
Kopčanský, P.; Tomašovičová, N.; Koneracká, M.; Timko, M.; Závišová, V.; Éber, N.; Fodor-Csorba, K.; Tóth-Katona, T.; Vajda, A.; Jadzyn, J.; Beaugnon, E.; Chaud, X. J. Magn. Magn. Mater. 2010, 322, 3696–3700. doi:10.1016/j.jmmm.2010.07.028
Return to citation in text: [1] -
Podoliak, N.; Buchnev, O.; Buluy, O.; D’Alessandro, G.; Kaczmarek, M.; Reznikov, Y.; Sluckin, T. J. Soft Matter 2011, 7, 4742–4749. doi:10.1039/C1SM05051F
Return to citation in text: [1] -
Buluy, O.; Nepijko, S.; Reshetnyak, V.; Ouskova, E.; Zadorozhnii, V.; Leonhardt, A.; Ritschel, M.; Schönhense, G.; Reznikov, Y. Soft Matter 2011, 7, 644–649. doi:10.1039/C0SM00131G
Return to citation in text: [1] -
Tomašovičová, N.; Timko, M.; Mitróová, Z.; Koneracká, M.; Rajňak, M.; Éber, N.; Tóth-Katona, T.; Chaud, X.; Jadzyn, J.; Kopčanský, P. Phys. Rev. E 2013, 87, 014501. doi:10.1103/PhysRevE.87.014501
Return to citation in text: [1] -
Martinez-Miranda, L. J.; Kurihara, L. K. J. Appl. Phys. 2009, 105, 084305. doi:10.1063/1.3086665
Return to citation in text: [1] -
Kopčanský, P.; Tomašovičová, N.; Koneracká, M.; Závišová, V.; Timko, M.; Hnatič, M.; Éber, N.; Tóth-Katona, T.; Jadzyn, J.; Honkonen, J.; Beaugnon, E.; Chaud, X. IEEE Trans. Magn. 2011, 47, 4409–4412. doi:10.1109/TMAG.2011.2160618
Return to citation in text: [1] -
Gdovinová, V.; Tomašovičová, N.; Éber, N.; Tóth-Katona, T.; Závišová, V.; Timko, M.; Kopčanský, P. Liq. Cryst. 2014, 41, 1773–1777. doi:10.1080/02678292.2014.950615
Return to citation in text: [1] -
Gorkunov, M. V.; Osipov, M. A. Soft Matter 2011, 7, 4348–4356. doi:10.1039/c0sm01398f
Return to citation in text: [1] -
Raikher, Y. L.; Stepanov, V. I.; Zakhlevnykh, A. N. Soft Matter 2013, 9, 177–184. doi:10.1039/C2SM26423D
Return to citation in text: [1] -
Makarov, D. V.; Zakhlevnykh, A. N. J. Magn. Magn. Mater. 2008, 320, 1312–1321. doi:10.1016/j.jmmm.2007.10.013
Return to citation in text: [1] -
Boychuk, A. N.; Zakhlevnykh, A. N.; Makarov, D. V. J. Exp. Theor. Phys. 2015, 121, 541–552. doi:10.1134/S1063776115090046
Return to citation in text: [1] -
Boychuk, A. N.; Makarov, D. V.; Zakhlevnykh, A. N. Eur. Phys. J. E 2016, 39, 101. doi:10.1140/epje/i2016-16101-y
Return to citation in text: [1] -
Boychuk, A. N.; Makarov, D. V.; Zakhlevnykh, A. N. J. Mol. Liq. 2017, 238, 359–369. doi:10.1016/j.molliq.2017.05.002
Return to citation in text: [1] -
Zakhlevnykh, A. N.; Lubnin, M. S.; Petrov, D. A. J. Magn. Magn. Mater. 2017, 431, 62–65. doi:10.1016/j.jmmm.2016.09.044
Return to citation in text: [1] -
Shoarinejad, S.; Ghazavi, M. Soft Mater. 2017, 15, 173–183. doi:10.1080/1539445X.2017.1287086
Return to citation in text: [1] -
Potisk, T.; Svenšek, D.; Brand, H. R.; Pleiner, H.; Lisjak, D.; Osterman, N.; Mertelj, A. Phys. Rev. Lett. 2017, 119, 097802. doi:10.1103/PhysRevLett.119.097802
Return to citation in text: [1] -
Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] -
Gray, G. W.; Harrison, K. J.; Nash, J. A. Electron. Lett. 1973, 9, 130–131. doi:10.1049/el:19730096
Return to citation in text: [1] -
Czechovski, G.; Czerkas, S.; Jadżyn, J. Z. Naturforsch., A 2001, 56, 257–261. doi:10.1515/zna-2001-0305
Return to citation in text: [1] -
Fundamentals of Magnetism and Magnetic Measurements. Featuring Quantum Design’s Magnetic Properties Measurement System. https://www.qdusa.com/sitedocs/appNotes/mpms/FundPrimer.pdf (accessed Oct 30, 2017).
Return to citation in text: [1]
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 1. | Jarkova, E.; Pleiner, H.; Müller, H.-W.; Brand, H. R. J. Chem. Phys. 2003, 118, 2422–2430. doi:10.1063/1.1533788 |
| 1. | Jarkova, E.; Pleiner, H.; Müller, H.-W.; Brand, H. R. J. Chem. Phys. 2003, 118, 2422–2430. doi:10.1063/1.1533788 |
| 7. | Jarkova, E.; Pleiner, H.; Müller, H.-W.; Fink, A.; Brand, H. R. Eur. Phys. J. E 2001, 5, 583–588. doi:10.1007/s101890170041 |
| 8. | Ryskin, A. B.; Pleiner, H.; Müller, H. W. Eur. Phys. J. E 2003, 11, 389–397. doi:10.1140/epje/i2003-10047-1 |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 4. | Burylov, S. V.; Raikher, Y. L. Mater. Sci. Eng., C 1995, 2, 235–241. doi:10.1016/0928-4931(95)00093-3 |
| 5. | Burylov, S. V.; Raikher, Y. L. Mol. Cryst. Liq. Cryst. 1995, 258, 107–122. doi:10.1080/10587259508034552 |
| 6. | Zakhlevnykh, A. N.; Petrov, D. A. J. Magn. Magn. Mater. 2016, 401, 188–195. doi:10.1016/j.jmmm.2015.10.025 |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 3. | Chen, S.-H.; Amer, N. M. Phys. Rev. Lett. 1983, 51, 2298–2301. doi:10.1103/PhysRevLett.51.2298 |
| 21. | Boychuk, A. N.; Zakhlevnykh, A. N.; Makarov, D. V. J. Exp. Theor. Phys. 2015, 121, 541–552. doi:10.1134/S1063776115090046 |
| 22. | Boychuk, A. N.; Makarov, D. V.; Zakhlevnykh, A. N. Eur. Phys. J. E 2016, 39, 101. doi:10.1140/epje/i2016-16101-y |
| 23. | Boychuk, A. N.; Makarov, D. V.; Zakhlevnykh, A. N. J. Mol. Liq. 2017, 238, 359–369. doi:10.1016/j.molliq.2017.05.002 |
| 24. | Zakhlevnykh, A. N.; Lubnin, M. S.; Petrov, D. A. J. Magn. Magn. Mater. 2017, 431, 62–65. doi:10.1016/j.jmmm.2016.09.044 |
| 25. | Shoarinejad, S.; Ghazavi, M. Soft Mater. 2017, 15, 173–183. doi:10.1080/1539445X.2017.1287086 |
| 2. | Brochard, F.; de Gennes, P. G. J. Phys. (Paris) 1970, 31, 691–708. doi:10.1051/jphys:01970003107069100 |
| 26. | Potisk, T.; Svenšek, D.; Brand, H. R.; Pleiner, H.; Lisjak, D.; Osterman, N.; Mertelj, A. Phys. Rev. Lett. 2017, 119, 097802. doi:10.1103/PhysRevLett.119.097802 |
| 15. | Martinez-Miranda, L. J.; Kurihara, L. K. J. Appl. Phys. 2009, 105, 084305. doi:10.1063/1.3086665 |
| 16. | Kopčanský, P.; Tomašovičová, N.; Koneracká, M.; Závišová, V.; Timko, M.; Hnatič, M.; Éber, N.; Tóth-Katona, T.; Jadzyn, J.; Honkonen, J.; Beaugnon, E.; Chaud, X. IEEE Trans. Magn. 2011, 47, 4409–4412. doi:10.1109/TMAG.2011.2160618 |
| 17. | Gdovinová, V.; Tomašovičová, N.; Éber, N.; Tóth-Katona, T.; Závišová, V.; Timko, M.; Kopčanský, P. Liq. Cryst. 2014, 41, 1773–1777. doi:10.1080/02678292.2014.950615 |
| 1. | Jarkova, E.; Pleiner, H.; Müller, H.-W.; Brand, H. R. J. Chem. Phys. 2003, 118, 2422–2430. doi:10.1063/1.1533788 |
| 20. | Makarov, D. V.; Zakhlevnykh, A. N. J. Magn. Magn. Mater. 2008, 320, 1312–1321. doi:10.1016/j.jmmm.2007.10.013 |
| 14. | Tomašovičová, N.; Timko, M.; Mitróová, Z.; Koneracká, M.; Rajňak, M.; Éber, N.; Tóth-Katona, T.; Chaud, X.; Jadzyn, J.; Kopčanský, P. Phys. Rev. E 2013, 87, 014501. doi:10.1103/PhysRevE.87.014501 |
| 8. | Ryskin, A. B.; Pleiner, H.; Müller, H. W. Eur. Phys. J. E 2003, 11, 389–397. doi:10.1140/epje/i2003-10047-1 |
| 12. | Podoliak, N.; Buchnev, O.; Buluy, O.; D’Alessandro, G.; Kaczmarek, M.; Reznikov, Y.; Sluckin, T. J. Soft Matter 2011, 7, 4742–4749. doi:10.1039/C1SM05051F |
| 13. | Buluy, O.; Nepijko, S.; Reshetnyak, V.; Ouskova, E.; Zadorozhnii, V.; Leonhardt, A.; Ritschel, M.; Schönhense, G.; Reznikov, Y. Soft Matter 2011, 7, 644–649. doi:10.1039/C0SM00131G |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 9. | Tomašovičová, N.; Koneracká, M.; Kopčanský, P.; Timko, M.; Závišová, V.; Jadzyn, J. Phase Transitions 2006, 79, 595–603. doi:10.1080/01411590600892633 |
| 10. | Kopčanský, P.; Tomašovičová, N.; Koneracká, M.; Závišová, V.; Timko, M.; Džarová, A.; Šprincová, A.; Éber, N.; Fodor-Csorba, K.; Tóth-Katona, T.; Vajda, A.; Jadzyn, J. Phys. Rev. E 2008, 78, 011702. doi:10.1103/PhysRevE.78.011702 |
| 11. | Kopčanský, P.; Tomašovičová, N.; Koneracká, M.; Timko, M.; Závišová, V.; Éber, N.; Fodor-Csorba, K.; Tóth-Katona, T.; Vajda, A.; Jadzyn, J.; Beaugnon, E.; Chaud, X. J. Magn. Magn. Mater. 2010, 322, 3696–3700. doi:10.1016/j.jmmm.2010.07.028 |
| 18. | Gorkunov, M. V.; Osipov, M. A. Soft Matter 2011, 7, 4348–4356. doi:10.1039/c0sm01398f |
| 19. | Raikher, Y. L.; Stepanov, V. I.; Zakhlevnykh, A. N. Soft Matter 2013, 9, 177–184. doi:10.1039/C2SM26423D |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 28. | Gray, G. W.; Harrison, K. J.; Nash, J. A. Electron. Lett. 1973, 9, 130–131. doi:10.1049/el:19730096 |
| 29. | Czechovski, G.; Czerkas, S.; Jadżyn, J. Z. Naturforsch., A 2001, 56, 257–261. doi:10.1515/zna-2001-0305 |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 27. | Tomašovičová, N.; Kováč, J.; Raikher, Y.; Éber, N.; Tóth-Katona, T.; Gdovinová, V.; Jadzyn, J.; Pinčák, R.; Kopčanský, P. Soft Matter 2016, 12, 5780–5786. doi:10.1039/C6SM00354K |
| 30. | Fundamentals of Magnetism and Magnetic Measurements. Featuring Quantum Design’s Magnetic Properties Measurement System. https://www.qdusa.com/sitedocs/appNotes/mpms/FundPrimer.pdf (accessed Oct 30, 2017). |
© 2017 Tomašovičová et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Nanotechnology terms and conditions: (http://www.beilstein-journals.org/bjnano)