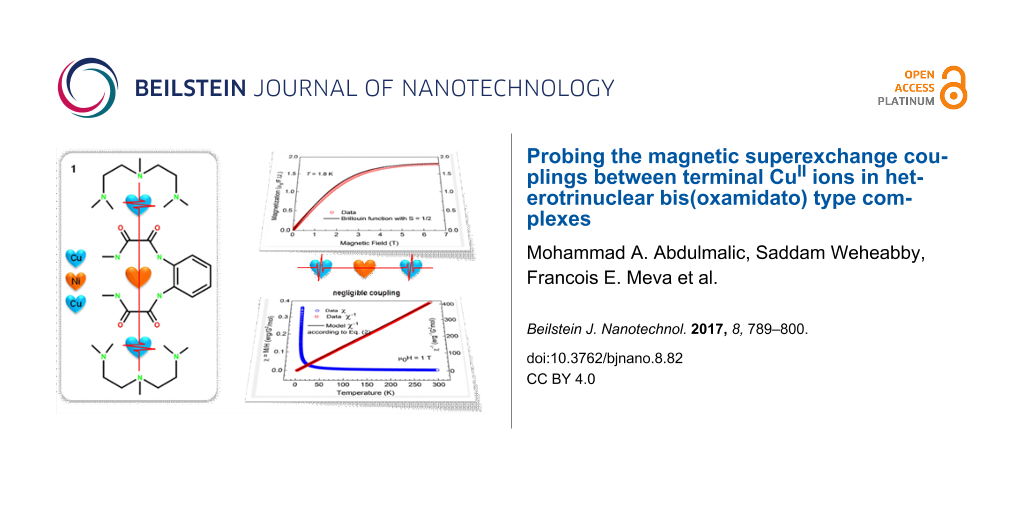
Abstract
The reaction of one equivalent of [n-Bu4N]2[Ni(opboR2)] with two equivalents of [Cu(pmdta)(X)2] afforded the heterotrinuclear CuIINiIICuII containing bis(oxamidato) type complexes [Cu2Ni(opboR2)(pmdta)2]X2 (R = Me, X = NO3– (1); R = Et, X = ClO4– (2); R = n-Pr, X = NO3– (3); opboR2 = o-phenylenebis(NR-substituted oxamidato); pmdta = N,N,N’,N”,N”-pentamethyldiethylenetriamine). The identities of the heterotrinuclear complexes 1–3 were established by IR spectroscopy, elemental analysis and single-crystal X-ray diffraction studies, which revealed the cationic complex fragments [Cu2Ni(opboR2)(pmdta)2]2+ as not involved in any further intermolecular interactions. As a consequence thereof, the complexes 1–3 possess terminal paramagnetic [Cu(pmdta)]2+ fragments separated by [NiII(opboR2)]2– bridging units representing diamagnetic SNi = 0 states. The magnetic field dependence of the magnetization M(H) of 1–3 at T = 1.8 K has been determined and is shown to be highly reproducible with the Brillouin function for an ideal paramagnetic spin = 1/2 system, verifying experimentally that no magnetic superexchange couplings exists between the terminal paramagnetic [Cu(pmdta)]2+ fragments. Susceptibility measurements versus temperature of 1–3 between 1.8–300 K were performed to reinforce the statement of the absence of magnetic superexchange couplings in these three heterotrinuclear complexes.
Introduction
Significant synthetic efforts have been directed to the synthesis of polynuclear species in which the metal ions are bridged by oxamato, oxamido, oxalato or dithiooxalato ligand [1-4]. In this context, the so-called bis(oxamato) type transition metal complexes as mononuclear species (Figure 1, type I) have received very special attention, as they allow the synthesis of multidimensional nD (n = 0–3) products, of which the magnetic properties were of specific interest [5]. Bis(oxamidato) type complexes (Figure 1, type II) have, on the other hand, received much less attention [6-9], although the flexidentate properties of these as well as type I complexes allows the convenient synthesis of the trinuclear type III and IV complexes, cf. Figure 1 [5,10,11].
Figure 1: Chemical structures of type I–IV complexes.
Figure 1: Chemical structures of type I–IV complexes.
The magnetic characterization of type III complexes has already significantly contributed to a better understanding of the origin of magnetic exchange interactions in polynuclear complexes [5,12]. One could expect that due to the lower electronegativity of the nitrogen atoms of type III (compared to the oxygen atoms of type IV complexes), the magnetic exchange couplings should increase [1]. These are studies to which we have already contributed [13-18].
Basically, one can expect different magnetic exchange pathways between the paramagnetic metal ions of type III and IV complexes as depicted in Figure 2a and consequently these complexes might possess three different pathways in case that they are composed of three nonequivalent metal ions. To some extent, that has been already shown for heterotrinuclear MnIICuIIMnII (S = 9/2) and NiIICuIINiII (S = 3/2) type III complexes [19-21]. Thus, by locating a small local between two large spins (Figure 2b), complexes with high-spin ground states can been obtained.
![[2190-4286-8-82-2]](/bjnano/content/figures/2190-4286-8-82-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Expected J couplings between the central and terminal paramagnetic metal ions in type III/IV complexes (a). Approach of a small local spin located between two large local spins (b).
Figure 2: Expected J couplings between the central and terminal paramagnetic metal ions in type III/IV comple...
If we follow this idea further we could replace the middle local spin, cf. Figure 2b, by a diamagnetic fragment. This would allow unambiguous verification of whether type III/IV complexes might have J1,3 magnetic couplings (Figure 2a) or not. There is already a first study of Sanada et al. [11], who reported for the heterotrinuclear GdIIINiIIGdIII type IV complex (S = 7/2) a very small J1,3 coupling of −0.002 cm–1. However, this small coupling might be attributed to the shielding effect of the outer-shell electrons on the 4f electron of the GdIII ions [11]. On the other hand, for homotrinuclear CuIICuIICuII type III complexes, J1,3 couplings were either assumed to be zero or negligible [14-16,22]. One can thus conclude that J1,3 couplings are very small.
In our earlier work, we previously reported on the magnetic characterization of homotrinuclear CuIICuIICuII type IV complexes [15]. We noticed, unexpectedly, that the central CuII ions of these complexes were not coordinated by any counter ions or solvents. It is this finding which gave birth to the idea to report here on the synthesis of heterotrinuclear CuIINiIICuII type IV complexes. Their central [NiII(opboR2)]2– fragments were anticipated to be free of any further co-ligands. That would make these central fragments purely diamagnetic and thus these heterotrinuclear CuIINiIICuII type IV complexes, possessing terminal paramagnetic CuII ions, appear as ideal candidates to study the magnitude of the J1,3 coupling of type III/IV complexes.
Results and Discussion
Synthesis
The synthesis of the heterotrinuclear CuIINiIICuII complexes 1–3 out of literature-known precursors is shown in Scheme 1.
Scheme 1: Synthesis of the heterotrinuclear CuIINiIICuII type IV complexes 1–3.
Scheme 1: Synthesis of the heterotrinuclear CuIINiIICuII type IV complexes 1–3.
Under anaerobic working conditions one equivalent of the non-hygroscopic [n-Bu4N]+ salts of mononuclear [NiII(opboR2)]2– complexes were treated with two equivalents of [Cu(pmdta)(X)2] (X = NO3– for 1 and 3, X = ClO4– for 2) in MeCN solutions of to give [NiCu2(opboR)(pmdta)2](X)2 (1–3, cf. Scheme 1) in yields exceeding 60%. The reaction side products [n-Bu4N][NO3] and [n-Bu4N][ClO4], respectively, could be smoothly separated as they are soluble in 4:1 THF/Et2O mixtures, while the desired complexes 1–3 are insoluble in such mixtures. The isolated powders of 1–3 had to be stored under inert gas atmosphere, as they are hygroscopic. Single crystals of 1–3 could be obtained as described next by crystallisation experiments performed under inert atmosphere.
Single crystal X-ray diffraction studies
Slow diffusion of Et2O vapour into CH2Cl2 solutions of 1 and 3 and into a MeCN solution of 2 afforded single crystals suitable for crystallographic studies of the compositions [{NiCu2(opboMe2)(pmdta)2}2][NO3]4·3.75CH2Cl2 (1’), [NiCu2(opboMe2)(pmdta)2][ClO4]2·2MeCN (2’) and [NiCu2(opboMe2)(pmdta)2][NO3]2·2CH2Cl2 (3’). In case of 1’, the asymmetric unit comprises two crystallographically independent complexes of 1. Their dicationic complex fragments [Cu2Ni(opboMe2)(pmdta)2]2+ are denoted in the following as 1A (comprising Ni1) and 1B (comprising Ni2). The related bond lengths and angles of 1A/1B show differences of up to 1.5% and ca. 2%, respectively, whereby only bond lengths and angles of 1A will be discussed, although Table 1 and Table 2 displays them for both 1A and 1B. In analogy, the cationic complex fragments [NiCu2(opboMe2)(pmdta)2]2+ of 2’ and [NiCu2(opboMe2)(pmdta)2]2+ of 3’ are denoted in the following as 2A and 3A. It should be highlighted and emphasized that in the crystal structures of 1’–3’ no unusual short intermolecular interactions were observed and that the complex fragments 1A–3A are indeed discrete.
Table 1: Selected bond lengths (Å) and angles (°) of the [Ni(opboR2)]2– fragments of 1A/1B (R = Me), 2A (R = Et) and 3A (R = n-Pr).
| 1A/1B | 2A | 3A | |
|---|---|---|---|
| Bond lengths | |||
| N1–Ni1 | 1.865(6)/1.862(6) | 1.869(6) | 1.847(5) |
| N2–Ni1 | 1.915(6)/1.912(7) | 1.922(6) | 1.904(6) |
| N3–Ni1(N1A–Ni1)a | 1.866(6)/1.867(6) | 1.860(6) | 1.847(5) |
| N4–Ni1(N2A–Ni1)a | 1.923(6)/1.922(7) | 1.923(6) | 1.904(6) |
| C1–O1 | 1.260(8)/1.238(9) | 1.259(10) | 1.264(8) |
| C2–O2 | 1.280(8)/1.300(9) | 1.261(9) | 1.289(8) |
| C3–O3(C1A–O1A)a | 1.255(8)/1.248(9) | 1.237(9) | 1.264(8) |
| C4–O4 (C2A–O2A)a | 1.279(8)/1.280(9) | 1.278(9) | 1.289(8) |
| C1–N1 | 1.316(9)/1.325(10) | 1.315(10) | 1.317(8) |
| C2–N2 | 1.280(9)/1.288(10) | 1.333(10) | 1.326(9) |
| C3–N3(C1A–N1A)a | 1.308(9)/1.303(10) | 1.331(10) | 1.317(8) |
| C4–N4(C2A–N2A)a | 1.304(9)/1.281(11) | 1.298(10) | 1.326(9) |
| C1–C2 | 1.535(9)/1.522(10) | 1.492(11) | 1.487(11) |
| C3–C4(C1A–C2A)a | 1.514(9)/1.533(10) | 1.515(11) | 1.487(11) |
| Bond angles | |||
| N1–Ni1–N3(N1–Ni1–N1A)a | 83.7(2)/83.7(3) | 83.7(3) | 83.5(3) |
| N2–Ni1–N4(N2–Ni1–N2A)a | 107.1(2)/107.5(3) | 107.5(3) | 107.0(4) |
| N1–Ni1–N2 | 84.6(2)/84.4(3) | 84.4(3) | 85.0(2) |
| N3–Ni1–N4(N1A–Ni1–N2A)a | 84.7(2)/84.3(3) | 84.5(3) | 85.0(2) |
| N1–Ni1–N4(N1–Ni1–N2A)a | 167.8(2)/167.6(3) | 168.0(3) | 166.9(2) |
| N2–Ni1–N3(N2–Ni1–N1A)a | 168.2(2)/168.0(3) | 167.9(3) | 166.9(2) |
| N1–C1–O1 | 129.7(6)/129.9(7) | 128.7(8) | 128.2(7) |
| N2–C2–O2 | 127.1(6)/126.7(7) | 125.0(7) | 126.3(7) |
| N3–C3–O3(N1A–C1A–O1A)a | 129.6(6)/129.5(7) | 128.7(7) | 128.2(7) |
| N4–C4–O4(N2A–C2A–O2A)a | 126.1(6)/127.8(7) | 126.9(7) | 126.3(7) |
aData in brackets refer to respective bond lengths and angles of 10A. Symmetry operation used to generate equivalent atoms ‘A’ for 10A: –x, y, –z + 3/2.
Table 2: Selected bond lengths (Å), angles (°) and τ parameters of the terminal [Cu(pmdta)]2+ fragments of 1A/1B (R = Me), 2A (R = Et) and 3A (R = n-Pr).
| 1A/1B | 2A | 3A | |
|---|---|---|---|
| Bond lengths | |||
| Cu1–O1 | 2.243(5)/2.218(5) | 2.210(5) | 2.192(5) |
| Cu1–O2 | 1.957(5)/1.953(5) | 1.998(6) | 1.982(5) |
| Cu1–N5 | 2.047(6)/2.061(6) | 2.070(8) | 2.077(6) |
| Cu1–N6 | 2.028(7)/1.997(7) | 2.015(7) | 2.010(6) |
| Cu1–N7 | 2.072(6)/2.090(6) | 2.035(7) | 2.029(6) |
| Cu2–O3 | 2.198(5)/2.203(5) | 2.198(5) | –a |
| Cu2–O4 | 1.962(5)/1.957(6) | 1.994(5) | –a |
| Cu2–N8 | 2.042(6)/2.044(7) | 2.056(6) | –a |
| Cu2–N9 | 2.010(6)/2.007(10) | 2.014(6) | –a |
| Cu2–N10 | 2.091(6)/2.082(9) | 2.072(7) | –a |
| Bond angles | |||
| O1–Cu1–O2 | 81.78(17)/82.2(2) | 81.1(2) | 81.80(19) |
| O1–Cu1–N5 | 99.1(2)/98.7(3) | 99.5(3) | 99.5(2) |
| O1–Cu1–N6 | 105.9(2)/104.1(2) | 104.3(3) | 101.6(2) |
| O1–Cu1–N7 | 103.7(2)/105.6(2) | 106.4(3) | 107.6(2) |
| O2–Cu1–N5 | 94.0(2)/95.0(3) | 92.8(3) | 92.9(2) |
| O2–Cu1–N6 | 172.0(2)/173.1(2) | 174.6(3) | 176.6(3) |
| O2–Cu1–N7 | 90.4(2)/89.7(3) | 91.8(3) | 92.6(2) |
| N5–Cu1–N6 | 87.0(3)/86.9(3) | 86.3(3) | 86.3(3) |
| N5–Cu1–N7 | 157.2(3)/155.6(3) | 154.1(3) | 152.8(3) |
| N6–Cu1–N7 | 85.6(3)/86.0(3) | 86.7(3) | 86.7(3) |
| O3–Cu2–O4 | 81.75(18)/81.9(2) | 81.4(2) | –a |
| O3–Cu2–N8 | 101.0(2)/102.0(3) | 104.2(2) | –a |
| O3–Cu2–N9 | 104.4(2)/105.3(3) | 102.8(2) | –a |
| O3–Cu2–N10 | 101.8(2)/100.5(3) | 100.2(2) | –a |
| O4–Cu2–N8 | 92.4(2)/91.3(3) | 92.5(2) | –a |
| O4–Cu2–N9 | 173.8(2)/172.8(3) | 175.8(3) | –a |
| O4–Cu2–N10 | 92.4(2)/90.3(4) | 93.0(2) | –a |
| N8–Cu2–N9 | 86.5(2)/86.5(4) | 86.2(3) | –a |
| N8–Cu2–N10 | 157.1(3)/157.4(3) | 155.6(3) | –a |
|
N9–Cu2–N10
τ parameter Cu1 |
86.3(3)/89.1(5)
0.247/0.292 |
86.6(3)
0.342 |
–a
0.397 |
| Cu2 | 0.278/0256 | 0.337 | –a |
aData of this [Cu(pmdta)]2+ fragment corresponds to those of the [Cu(pmdta)]2+ fragment comprising the atom Cu1, due to the crystallographically imposed C2 symmetry of 3A.
The molecular structures of 1A–3A are similar to each other and thus structural features of all three complex fragments will be discussed together. A collective plot of the molecular structures of 1A–3A in an analogous perspective view is shown in Figure 3. Selected bond lengths and angles of the [Ni(opboR2)]2– and of the [Cu(pmdta)]2+ complex fragments of 1A–3A are given in Table 1 and Table 2, respectively. Crystal and structural refinement data are summarized in Table 3.
Table 3: Crystal and structural refinement data of 1’, 2’and 3’.
| 1’ | 2’ | 3’ | |
|---|---|---|---|
| Empirical formula | C255H478Cl30Cu16N96Ni8O80 | C36H66Cl2Cu2N12NiO12 | C36H68Cl4Cu2N12NiO10 |
| Formula weight (g·mol–1) | 8719.15 | 1115.69 | 1156.61 |
| Crystal system | orthorhombic | triclinic | orthorhombic |
| Space group | Pbca | P−1 | Pbcn |
| a (Å) | 35.6630(14) | 8.2749(3) | 29.485(2) |
| b (Å) | 14.0366(7) | 10.9892(3) | 11.2595(13) |
| c (Å) | 37.5448(16) | 30.1863(10) | 16.0310(13) |
| α (°) | 90.0 | 83.352(3) | 90.0 |
| β (°) | 90.0 | 82.706(3) | 90.0 |
| γ (°) | 90.0 | 70.178(3) | 90.0 |
| V (Å−3) | 18810.3(14) | 2553.65(15) | 5322.1(8) |
| Measurement temperature (K) | 110 | 115 | 110 |
| Radiation source | Cu Kα | Cu Kα | Cu Kα |
| Wavelength (Å) | 1.54184 | 1.54184 | 1.54184 |
| Z | 2 | 2 | 4 |
| Density (calculated) (Mg·m–3) | 1.539 | 1.451 | 1.443 |
| Absorption coefficient (mm–1) | 4.008 | 2.912 | 3.687 |
| F(000) | 9036 | 1164 | 2408 |
| Reflections collected | 53695 | 10264 | 10911 |
| Reflections unique /Rinta | 15422, 0.0475 | 10264, 0.0412 | 4212, 0.0462 |
| Limiting indices | –23 ≤ h ≤ 41, | –9 ≤ h ≤ 9, | –32≤ h ≤ 34, |
| –16 ≤ k ≤ 11, | –12 ≤ k ≤ 12, | –12 ≤ k ≤ 12, | |
| –43 ≤ l ≤ 42 | –34 ≤ l ≤ 31 | –18 ≤ l ≤ 15 | |
| θ range for data collection (°) | 3.417 to 62.981 | 4.290 to 62.706 | 4.203 to 62.744 |
| Data/restraints/parameters | 15422/1164/1126 | 10264/662/645 | 4212/289/292 |
| Goodness-of-fit on F2 b | 0.938 | 1.101 | 0.830 |
| Final R indices [I > 2σ(I)]c |
R1 = 0.0816,
wR2 = 0.2279 |
R1 = 0.0777,
wR2 = 0.2073 |
R1 = 0.0810,
wR2 = 0.2120 |
| R indices (all data)c |
R1 = 0.1234,
wR2 = 0.2460 |
R1 = 0.0816,
wR2 = 0.2097 |
R1 = 0.1364,
wR2 = 0.2337 |
| Largest diff. peak/hole (e·Å–3) | 1.988/−1.311 | 1.132/−0.549 | 0.925/−0.868 |
aRint = Σ│Fo2–Fo2(mean)│/ΣFo2, where Fo2(mean) is the average intensity of symmetry equivalent diffractions. bS = [∑w(Fo2 – Fc2)2]/(n – p)1/2, where n = number of reflections, p = number of parameters. cR = [∑(||Fo| – |Fc|)/∑|Fo|); wR = [∑(w(Fo2 – Fc2)2)/∑(wFo4)]1/2.
![[2190-4286-8-82-3]](/bjnano/content/figures/2190-4286-8-82-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3:
ORTEP diagrams (50% ellipsoid probability) of the molecular structures of 1A (top), 2A (middle) and 3A (down), respectively. All hydrogen atoms are omitted for clarity. The sign refers to the interplanar angle, rmsd to the root-mean-square deviation from planarity and hdp to the highest deviation from planarity of calculated mean planes of atoms adjoining differently coloured areas. Symmetry code ‘A’ for 10A: –x, y, –z + 3/2. The rmsd/hdp of atoms adjoining light gray and black coloured areas amounts as follows: 8A, 0.118 Å/Cu1 with 0.410 Å. 9A, 0.064 Å/O2 with 0.135 Å. 10A, 0.107 Å/O2 with 0.207 Å.
Figure 3: ORTEP diagrams (50% ellipsoid probability) of the molecular structures of 1A (top), 2A (middle) and ...
The NiII ions of 1A–3A are coordinated by four deprotonated amide N donor atoms to form a planar-quadratic NiN4 coordination environment. Two of them belong to the N,N’-o-phenylene bridges of 1A–3A (1A/2A: N1 and N3. 3A: N1 and N1A) and are referred to in the following as Naryl donor atoms. The other two belong to the alkyl-substituted amide functions of 1A–3A (1A/2A: N2 and N4. 3A: N2 and N2A) and are further referred to as Nalkyl donor atoms. The planarity of the NiN4 units is revealed, for example, by calculations of mean planes of its atoms and gives the following root-mean-square deviations from planarity (rmsd) together with values for the atom with the highest deviation from planarity (hdp) as follows: 1A/2A/3A (rmsd, hdp) = 0.035 Å, N1 with 0.046(3) Å /0.030 Å, N1 with 0.035(8) Å/0.082 Å, N1 with 0.100(4) Å, respectively. Moreover, the sum of bond angles of the NiN4 units amounts to 360.1(4)° (1A), 360.1(6)° (2A) and 360.5(5)° (3A). For the mononuclear NiII-containing bis(oxamato) complex [n-Bu4N]2[Ni(opba)] (11) [23] and the related bis(oxamidato) type complex [Ph4P]2[Ni(opboMe2)] (12) [9] the following observation has been made: Three of bond angles of the central NiN2O2/NiN4 coordination units are small (11: 85.79(8)–86.18(5)°; 12: 82.7(3)–84.7(3)°), while the fourth one is significantly larger (11: 101.97(7)°; 12: 108.8(3)°). Thereby, the latter bond angle is the one created of the two carboxylate oxygen atoms of 11 or the two Nalkyl donor atoms of 12. This feature is due to the presence of 5-5-5 fused chelate rings around the NiII ion [17,24]. In case of 1A–3A this feature is observed as well, cf. Table 1.
The Ni–N bond lengths of the NiN4 units of 1A–3A fall into two categories: The Ni–Naryl bond lengths are significantly shorter compared to the Ni–Nalkyl ones [25]. For example, the Ni–Naryl bond lengths of 1A (Ni1–N1 and Ni1–N3, = 1.864(8) Å) are substantially shorter compared to the Ni–Nalkyl bond lengths (Ni1–N2 and Ni1–N4,
= 1.912(8) Å). This fact is in principal in agreement with the observations made for 12 [9] and could be explained in analogy to statements made for mononuclear CuII-containing bis(oxamato) complexes by the greater basicity of the Naryl vs the Nalkyl donor atoms [24].
In the following the geometries of the terminal [Cu(pmdta)]2+ fragments will be briefly described. It should be emphasized that the findings described in the following have been made analogously for our previously reported homotrinuclear CuIICuIICuII complexes as described in [15]. Thus, the terminal CuII ions of 1A–3A are each coordinated by two O donor atoms of the oxamidato groups as well as three N donor atoms of the pmdta ligands to form CuN3O2 coordination units closer to the ideal square-pyramidal compared to the ideal trigonal-bipyramidal coordination geometry with respect to their τ parameters [26], cf. Table 2. One feature, commonly observed for all CuN3O2 units, deserves specific attention. The largest bond angle of all CuN3O2 units always involves the O donor atom of the function and the middle N donor atom of the pmdta ligands, cf. Figure 1 and Table 2. A related observation was made recently for the asymmetric trinuclear complex [Cu3(opooMe)(pmdta)2](NO3)2 (13, opooMe = o-phenylene(N’-methyl oxamidato)(oxamato)) [13] and has been compared to observations made for bis(oxamato) type entities. As observed for the CuN3O2 units of 1A–3A, even in the case of 13, the largest O–Cu–N bond angle involves the O donor atom of the
function for the oxamidato side, whereas in case of the oxamato side the largest bond angle involves the O donor atom of the
function. Consequences of this observation to magnetic exchange couplings have been discussed [13]. Thus, it seems that for polynuclear complexes comprising one or two oxamidato groups, cf. [13] and [15], this specific feature of the terminal CuN3O2 units is of broader validity.
It is recalled that the NiII ions of 1A–3A are not coordinated further by any counter anions and/or solvent molecules. In contrast, in CuIICuIICuII type III complexes (Figure 1) the central CuII ions are commonly further coordinated, even by BF4– ions [14]. Hence, the NiII ions of 1A–3A indeed represent diamagnetic SNi = 0 states. Specifically, this property makes them excellently suited candidates to experimentally verify whether long-range magnetic superexchange interactions along two consecutively aligned oxamidato and even oxamato bridges are possible.
Magnetic properties
The results of the measurements of the magnetic field dependence of the magnetization M(H) for samples 1, 2 and 3 at T = 1.8 K are shown in Figure 4, Figure 5 and Figure 6. All curves can be very well fitted with the Brillouin function for spin S = 1/2 and the spectroscopic g-factor g = 2.1 determined from the electron spin resonance (ESR) spectra (not shown):
Here, NS=1/2 is the number of spins 1/2 in the molecule, µB is the Bohr magneton, and kB is the Boltzmann constant. Considering that Equation 1 describes the behavior of an ideal paramagnet comprising non-interacting spins and that Equation 1 nicely reproduces the shape of the measured M(H) dependences, one can safely conclude that at T = 1.8 K and (within the experimental uncertainty) there is no magnetic interaction between the CuII spins of the terminal [Cu(pmdta)]2+ complex fragments in all three samples. At fields above 5 T, all M(H) curves saturate, cf. Figure 4–6. Under these experimental conditions one has gSµBH/kBT >> 1 and Equation 1 thus reduces to Msat(H) = NS=1/2gSµB for the heterotrinuclear 1–3 with NS=1/2 = 2. Therefore, the expected saturation magnetization for S = 1/2 and g = 2.1 should amount to Msat(H) = 2.1µB per formula unit (f.u.). The experimentally observed values of Msat(H) are somewhat smaller, amounting to 1.91µB, 1.79µB, and 1.85µB for 1, 2 and 3, respectively. This implies that the effective number of non-interacting CuII spins per f.u. which contribute to the magnetization signal is smaller than NS=1/2 = 2 and amounts to = 1.82, 1.7, and 1.76 for 1, 2 and 3, respectively. This discrepancy of the order of ≈10% in average could be attributed to remaining amounts of packing solvent molecules and thus errors in the determination of the molecular weight. It could be attributed furthermore to the hygroscopic nature of vacuum-dried single crystals of 1’–3’ and as the sample preparation was performed under aerobic conditions, cf. Experimental Section and Supporting Information File 1, giving thus errors in the determination of the molecular weight of the samples.
![[2190-4286-8-82-4]](/bjnano/content/figures/2190-4286-8-82-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: Magnetization versus magnetic field M(H) of 1 at T = 1.8 K (symbols) together with the fit of M(H) to the Brillouin function with S = 1/2 according to Equation 1 (solid line).
Figure 4: Magnetization versus magnetic field M(H) of 1 at T = 1.8 K (symbols) together with the fit of M(H) ...
![[2190-4286-8-82-5]](/bjnano/content/figures/2190-4286-8-82-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: Magnetization versus magnetic field M(H) of 2 at T = 1.8 K (symbols) together with the fit of M(H) to the Brillouin function with S = 1/2 according to Equation 1 (solid line).
Figure 5: Magnetization versus magnetic field M(H) of 2 at T = 1.8 K (symbols) together with the fit of M(H) ...
![[2190-4286-8-82-6]](/bjnano/content/figures/2190-4286-8-82-6.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: Magnetization versus magnetic field M(H) of 3 at T = 1.8 K (symbols) together with the fit of M(H) to the Brillouin function with S = 1/2 according to Equation 1 (solid line).
Figure 6: Magnetization versus magnetic field M(H) of 3 at T = 1.8 K (symbols) together with the fit of M(H) ...
Further insights into the magnetism of the studied samples can be obtained from the analysis of the temperature dependence of the static magnetic susceptibility χ = M/H. The curves χ(T) and the corresponding inverse susceptibility χ−1(T) for 1, 2 and 3 are presented in Figure 7–9. These dependences for 1 and 2 can be very well understood in terms of the Curie–Weiss law:
Here, χ0 is a temperature independent term comprising the van Vleck and diamagnetic susceptibilities, NA is the Avogadro number, and θ is the Curie–Weiss temperature which is a measure of the magnetic interaction between the spins. Since the analysis of the M(H) curves reveal no interaction between CuII spins, θ can be assumed zero. With S = 1/2, g = 2.1 and the values of from the saturation magnetization Msat(H) one can calculate the dependence (Equation 2) versus
as plotted in black in Figure 7 and Figure 8. Obviously, the plots agree well with the experimental dependence χ−1(T) for 1 and 2. Here, the values χ0 = 5·10–5 erg/G2/mol and 1·10–4 erg/G2/mol were chosen for samples 1 and 2, respectively. From the above discussion one can therefore conclude that the self-consistent analysis of the M(H) and χ(T) dependences gives evidence for the absence of magnetic interaction between the terminal CuII ions in the heterotrinuclear CuIINiIICuII complexes 1 and 2.
![[2190-4286-8-82-7]](/bjnano/content/figures/2190-4286-8-82-7.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 7:
Temperature dependence of the magnetic susceptibility χ = M/H and of the corresponding inverse susceptibility χ−1 for 1 (symbols). The black line represents a model curve according to Equation 2 (see the text).
Figure 7: Temperature dependence of the magnetic susceptibility χ = M/H and of the corresponding inverse susc...
![[2190-4286-8-82-8]](/bjnano/content/figures/2190-4286-8-82-8.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 8:
Temperature dependence of the magnetic susceptibility χ = M/H and of the corresponding inverse susceptibility χ−1 for 2 (symbols). The black line represents a model curve according to Equation 2 (see the text).
Figure 8: Temperature dependence of the magnetic susceptibility χ = M/H and of the corresponding inverse susc...
Unfortunately, no definite conclusion can be drawn for complex 3. The similarly calculated curve according to Equation 2 is shown by the black solid curve in Figure 9. It strongly deviates from the measured χ−1(T) dependence. Correspondingly, the product χ(T)T increases with temperature (Figure 10, inset). There is obviously an additional contribution to the static susceptibility, leading to lower values of the inverse susceptibility
of the sample. This contribution is absent in the magnetization data at T = 1.8 K, suggesting that it may originate from some species in a concentration of the order of 10% with thermally activated magnetism. The difference Δχ = χexp − χcal is plotted in Figure 10, main panel, and might originate from paramagnetic impurities, cf. [16]. On the other hand, vacuum-dried powders of 3’ appeared as more hygroscopic compared to the ones of 1’ and 2’, cf. above and Supporting Information File 1. As the sample preparation was performed under aerobic conditions, it is imaginable that air moisture had an impact on these measured as it is shown for the IR spectroscopically characterized 3. Attempts to model this contribution with some specific models invoking possible exchange interactions between the two Cu centers (e.g., [13,15,27]) were not successful.
![[2190-4286-8-82-9]](/bjnano/content/figures/2190-4286-8-82-9.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 9:
Temperature dependence of the magnetic susceptibility χ = M/H and of the corresponding inverse susceptibility χ−1 for 3. The black line represents a model curve according to Equation 2 (see the text). The dashed arrow indicates the discrepancy between the model curve and the experimental dependence.
Figure 9: Temperature dependence of the magnetic susceptibility χ = M/H and of the corresponding inverse susc...
![[2190-4286-8-82-10]](/bjnano/content/figures/2190-4286-8-82-10.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 10: Main panel: Difference between the calculated and measured static susceptibility for 3. Inset: Temperature dependence of the product χT for 3 (see the text).
Figure 10: Main panel: Difference between the calculated and measured static susceptibility for 3. Inset: Temp...
Conclusion
The three heterotrinuclear bis(oxamidato) type complexes comprising [Cu2Ni(opboR2)]2+ fragments (R = Me (1), Et (2), n-Pr (3)) could be successfully synthesized and their identities have been unambiguously established by single-crystal X-ray diffraction studies. These studies revealed that all [Cu2Ni(opboR2)]2+ fragments are not involved in any intermolecular interactions and are thus discrete in the solid state. That made these three complexes especially well-suited to experimentally verify that there are no magnetic superexchange couplings between their terminal [Cu(pmdta)]2+ fragments. Thus, we can conclude that for trinuclear type IV as well as type III complexes incorporating exclusively 3d transition metal ions, no long-range magnetic couplings across two consecutively aligned oxamidato or oxamato bridges can occur.
Experimental
General methods and materials
All chemicals were purchased from commercial sources and used as received unless stated otherwise. All reactions were carried out under an atmosphere of dry argon using standard Schlenk techniques and vacuum-line manipulations unless stated otherwise. All solvents were distilled prior to use and were purified/dried according to standard procedures [28]. NMR spectra were recorded at room temperature with a Bruker Avance III 500 Ultra Shield Spectrometer (1H at 500.300 MHz and 13C{1H} at 125.813 MHz) in the Fourier transform mode. Chemical shifts are reported in δ (ppm) versus SiMe4 with the solvent as the reference signal ([D6]-DMSO: 1H NMR, δ = 2.54; and 13C{1H}NMR, δ = 40.45). FTIR spectra were recorded in the range of 400–4000 cm−1 on a Perkin-Elmer Spectrum 1000 FTIR spectrophotometer as KBr pellets. Elemental analysis for C, H and N were performed on a Thermo FlashAE 1112 series. The mononuclear NiII-containing complexes [n-Bu4N]2[Ni(opboR2)] (R = Me, Et, n-Pr) were synthesized according to the literature [15]. Static magnetization measurements at T = 1.8 K and in magnetic fields µ0H up to 7 T were carried out with a 7 T VSM-SQUID magnetometer from Quantum Design. The temperature dependence of the static magnetization was measured in a temperature range T = 1.8–300 K and at µ0H = 1 T with this device. For these magnetic measurements, single crystals of the individual complexes were taken and gently heated (ca. 35 °C) overnight in vacuum to obtain materials free of packing solvents. Unfortunately, no inspection of the vacuum-dried crystals under the microscope was possible due to the hygroscopic nature of the materials, cf. below and Supporting Information File 1.
Singe-crystal X-ray crystallographic studies. Intensity data of 1’, 2’ and 3’, respectively, were collected on an Oxford Gemini S diffractometer with Cu Kα radiation. The structures were solved by direct methods and refined by full-matrix least-squares methods on F2 with the SHELX-2013 software [29]. All non-hydrogen atoms were refined anisotropically, and riding models were employed in the treatment of the hydrogen atom positions. Crystallographic data have been deposited at the Cambridge Crystallographic Data Center under the CCDC numbers 923899 (1’), 923898 (2’) and 923900 (3’). In case of 1’ one CH2Cl2 packing solvent molecule has been refined to an occupation factor of 0.75 (Cl7, Cl8, C61) and another CH2Cl2 packing solvent molecule (Cl5, Cl6, C64) has been refined disordered on two position with occupation factors of 0.75/0.25. In case of 2’ the two ClO4– counter ions were both refined disordered on two position with occupation factors of 0.61/0.39 (Cl1, O5–O8) and 0.50/0.50 (Cl2, O9–O12), respectively. Crystals of 2’ were all twinned. The selected one was composed of two nearly equally populated domains covering ca. 98% of all measured reflections, which were simultaneously integrated to generate a hklf 5 file with the diffractometer software [30]. In the case of 3’, the CH2Cl2 packing solvent molecule (Cl1, Cl2, C18) has been refined disordered on two position with occupation factors of 0.67/0.33.
Synthesis of [NiCu2(opboR2)(pmdta)2][X]2, R = Me, X = NO3 (1); R = Et, X = ClO4 (2), R = n-Pr, X = NO3 (3). To a solution of [n-Bu4N]2[Ni(opboR2)] (R = Me, nPr) or [n-Bu4N]2[Ni(opboEt2)] (0.0006 mol) in MeCN (50 mL) a solution of [Cu(pmdta)(NO3)2] (0.0012 mol) in MeCN (25 mL) or [Cu(pmdta)(ClO4)2] (0.0012 mol) in MeCN (25 mL) was added, respectively. After stirring for 1 h, the resulting reaction mixture was concentrated to approximately 5 mL and Et2O (100 mL) was added to give a green precipitate. The overlaying solvent mixture was removed via a Teflon tube and MeCN (5 mL) was added to dissolve the residue. A mixture of THF/Et2O 4:1 (100 mL) was added to precipitate a green powder, which was washed twice with the same solvents mixture (50 mL). After removal of the supernatant, the remaining solid was dried in vacuum. Crystals suitable for X-ray crystallographic studies were grown by slow diffusion of Et2O vapour in CH2Cl2 solutions of 1 and 3 and in a MeCN solution of 2. Supporting Information File 1 gives the IR spectra of 1–3, respectively.
1. Yield: 0.35 g (63%); anal. calcd for C30H56Cu2N12NiO10 (930.63 g·mol–1): C, 38.72; H, 6.07; N, 18.06; found: C, 38.22; H, 5.85; N, 17.92%; IR: ν = 2958 (m), 2946 (m) (CH); 1630 (s), 1602 (m) (CO); (1383) (s) ().
2. Yield: 0.44 g (77%); anal. calcd for C32H60Cl2Cu2N10NiO12 (1033.57 g·mol–1): C, 37.19; H, 5.85; N, 13.55; found: C, 37.22; H 5.74; N, 13.28%; IR: ν = 2983 (m), 2960 (m) (CH); 1653 (m), 1614 (m) (CO); (1061) (s) ().
3. Yield: 0.43 g (74%); anal. calcd for C34H64Cu2N12NiO10 (986.73 g·mol–1): C, 41.39; H, 6.54; N, 17.03; found: C, 41.11; H, 6.39; N, 16.89%; IR: ν = 2977 (m), 2951 (m) (CH); 1647 (s), 1614 (m) (CO); (1389) (s) ().
Supporting Information
| Supporting Information File 1: IR spectra of 1–3. | ||
| Format: PDF | Size: 369.0 KB | Download |
References
-
Kahn, O. Angew. Chem., Int. Ed. Engl. 1985, 24, 834–850. doi:10.1002/anie.198508341
Return to citation in text: [1] [2] -
Pei, Y.; Kahn, O.; Sletten, J. J. Am. Chem. Soc. 1986, 108, 3143–3145. doi:10.1021/ja00271a075
Return to citation in text: [1] -
Stumpf, H. O.; Pei, Y.; Kahn, O.; Sletten, J.; Renard, J. P. J. Am. Chem. Soc. 1993, 115, 6738–6745. doi:10.1021/ja00068a034
Return to citation in text: [1] -
Okawa, H.; Mitsumi, M.; Ohba, M.; Kodera, M.; Matsumoto, N. Bull. Chem. Soc. Jpn. 1994, 67, 2139–2144. doi:10.1246/bcsj.67.2139
Return to citation in text: [1] -
Pardo, E.; Ruiz-García, R.; Cano, J.; Ottenwaelder, X.; Lescouëzec, R.; Journaux, Y.; Lloret, F.; Julve, M. Dalton Trans. 2008, 2780–2805. doi:10.1039/b801222a
Return to citation in text: [1] [2] [3] -
Estrada, J.; Fernandez, I.; Pedro, J. R.; Ottenwaelder, X.; Ruiz, R.; Journaux, Y. Tetrahedron Lett. 1997, 38, 2377–2380. doi:10.1016/S0040-4039(97)00354-7
Return to citation in text: [1] -
Journaux, Y.; Ruiz, R.; Aukauloo, A.; Pei, Y. Mol. Cryst. Liq. Cryst. 1997, 305, 193–202. doi:10.1080/10587259708045056
Return to citation in text: [1] -
Ruiz, R.; Surville-Barland, C.; Aukauloo, A.; Anxolabehere-Mallart, E.; Journaux, Y.; Cano, J.; Muñoz, M. C. J. Chem. Soc., Dalton Trans. 1997, 745–752. doi:10.1039/A607572J
Return to citation in text: [1] -
Ottenwaelder, X.; Aukauloo, A.; Journaux, Y.; Carrasco, R.; Cano, J.; Cervera, B.; Castro, I.; Curreli, S.; Muñoz, M. C.; Roselló, A. L.; Soto, B.; Ruiz-García, R. Dalton Trans. 2005, 2516–2526. doi:10.1039/b502478a
Return to citation in text: [1] [2] [3] -
Ruiz, R.; Surville-Barland, C.; Journaux, Y.; Colin, J. C.; Castro, I.; Cervera, B.; Julve, M.; Lloret, F.; Sapiña, F. Chem. Mater. 1997, 9, 201–209. doi:10.1021/cm9602961
Return to citation in text: [1] -
Sanada, T.; Suzuki, T.; Kaizaki, S. J. Chem. Soc., Dalton Trans. 1998, 959–966. doi:10.1039/A706834D
Return to citation in text: [1] [2] [3] -
Kahn, O. Molecular Magnetism; VCH: New York, 1993. doi:10.1002/bbpc.19940980935
Return to citation in text: [1] -
Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Hahn, T.; Kortus, J.; Rüffer, T. Dalton Trans. 2012, 41, 14657–14670. doi:10.1039/c2dt31802d
Return to citation in text: [1] [2] [3] [4] [5] -
Rüffer, T.; Bräuer, B.; Powell, A. K.; Hewitt, I.; Salvan, G. Inorg. Chim. Acta 2007, 360, 3475–3483. doi:10.1016/j.ica.2007.03.037
Return to citation in text: [1] [2] [3] -
Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Zaripov, R.; Vavilova, E.; Voronkova, V.; Salikov, K.; Hahn, T.; Kortus, J.; Meva, F. E.; Schaarschmidt, D.; Rüffer, T. Dalton Trans. 2015, 44, 8062–8079. doi:10.1039/c4dt03579h
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] -
Rüffer, T.; Bräuer, B.; Meva, F. E.; Sorace, L. Inorg. Chim. Acta 2009, 362, 563–569. doi:10.1016/j.ica.2008.05.005
Return to citation in text: [1] [2] [3] -
Abdulmalic, M. A.; Rüffer, T. Bull. Chem. Soc. Jpn. 2013, 86, 724–728. doi:10.1246/bcsj.20130031
Return to citation in text: [1] [2] -
Abdulmalic, M. A. A Tailor-Made Approach for Thin Films and Monolayer Assemblies of bis (oxamato) and bis (oxamidato) Transition Metal Complexes. Ph.D. Thesis, Chemnitz University of Technology, Faculty of Natural Sciences, 2013.
Return to citation in text: [1] -
Pei, Y.; Journaux, Y.; Kahn, O. Inorg. Chem. 1988, 27, 399–404. doi:10.1021/ic00275a031
Return to citation in text: [1] -
Ribas, J.; Diaz, C.; Costa, R.; Journaux, Y.; Mathoniere, C.; Kahn, O.; Gleizes, A. Inorg. Chem. 1990, 29, 2042–2047. doi:10.1021/ic00336a003
Return to citation in text: [1] -
Wang, Q.-L.; Zhu, L.-N.; Liao, D.-Z.; Yan, S.-P.; Jiang, Z.-H.; Cheng, P.; Yang, G.-M. J. Mol. Struct. 2005, 754, 10–15. doi:10.1016/j.molstruc.2005.05.032
Return to citation in text: [1] -
Gao, E.-Q.; Zhao, Q.-H.; Tang, J.-K.; Liao, D.-Z.; Jiang, Z.-H.; Yan, S.-P. J. Chem. Soc., Dalton Trans. 2001, 1537–1540. doi:10.1039/B100142F
Return to citation in text: [1] -
Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Kataev, V.; Rüffer, T. Dalton Trans. 2013, 42, 1798–1809. doi:10.1039/C2DT32259E
Return to citation in text: [1] -
Cervera, B.; Sanz, J. L.; Ibáñez, M. J.; Vila, G.; Lloret, F.; Julve, M.; Ruiz, R.; Ottenwaelder, X.; Aukauloo, A.; Poussereau, S.; Journaux, Y.; Muñoz, M. C. J. Chem. Soc., Dalton Trans. 1998, 781–790. doi:10.1039/A706964B
Return to citation in text: [1] [2] -
Cruickshank, D. W. J. Acta Crystallogr. 1949, 2, 65–82. doi:10.1107/S0365110X49000175
Return to citation in text: [1] -
Addison, A. W.; Rao, T. N.; Reedijk, J.; van Rijn, J.; Verschoor, G. C. J. Chem. Soc., Dalton Trans. 1984, 1349–1356. doi:10.1039/DT9840001349
Return to citation in text: [1] -
Krupskaya, Y.; Alfonsov, A.; Parameswaran, A.; Kataev, V.; Klingeler, R.; Steinfeld, G.; Beyer, N.; Gressenbuch, M.; Kersting, B.; Büchner, B. ChemPhysChem 2010, 11, 1961–1970. doi:10.1002/cphc.200900935
Return to citation in text: [1] -
Perin, D. D.; Armarego, W. L. F. Purification of Laboratory Chemicals, 3rd ed.; Pergamon: New York, 1988.
Return to citation in text: [1] -
Sheldrick, G. M. Acta Crystallogr., Sect. A 2008, A64, 112–122. doi:10.1107/S0108767307043930
Return to citation in text: [1] -
Data collection, refinement and reduction software: CrysAlisPro, 1.171.38.41l ; Rigaku OD, 2015.
Return to citation in text: [1]
| 28. | Perin, D. D.; Armarego, W. L. F. Purification of Laboratory Chemicals, 3rd ed.; Pergamon: New York, 1988. |
| 15. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Zaripov, R.; Vavilova, E.; Voronkova, V.; Salikov, K.; Hahn, T.; Kortus, J.; Meva, F. E.; Schaarschmidt, D.; Rüffer, T. Dalton Trans. 2015, 44, 8062–8079. doi:10.1039/c4dt03579h |
| 29. | Sheldrick, G. M. Acta Crystallogr., Sect. A 2008, A64, 112–122. doi:10.1107/S0108767307043930 |
| 1. | Kahn, O. Angew. Chem., Int. Ed. Engl. 1985, 24, 834–850. doi:10.1002/anie.198508341 |
| 2. | Pei, Y.; Kahn, O.; Sletten, J. J. Am. Chem. Soc. 1986, 108, 3143–3145. doi:10.1021/ja00271a075 |
| 3. | Stumpf, H. O.; Pei, Y.; Kahn, O.; Sletten, J.; Renard, J. P. J. Am. Chem. Soc. 1993, 115, 6738–6745. doi:10.1021/ja00068a034 |
| 4. | Okawa, H.; Mitsumi, M.; Ohba, M.; Kodera, M.; Matsumoto, N. Bull. Chem. Soc. Jpn. 1994, 67, 2139–2144. doi:10.1246/bcsj.67.2139 |
| 5. | Pardo, E.; Ruiz-García, R.; Cano, J.; Ottenwaelder, X.; Lescouëzec, R.; Journaux, Y.; Lloret, F.; Julve, M. Dalton Trans. 2008, 2780–2805. doi:10.1039/b801222a |
| 12. | Kahn, O. Molecular Magnetism; VCH: New York, 1993. doi:10.1002/bbpc.19940980935 |
| 17. | Abdulmalic, M. A.; Rüffer, T. Bull. Chem. Soc. Jpn. 2013, 86, 724–728. doi:10.1246/bcsj.20130031 |
| 24. | Cervera, B.; Sanz, J. L.; Ibáñez, M. J.; Vila, G.; Lloret, F.; Julve, M.; Ruiz, R.; Ottenwaelder, X.; Aukauloo, A.; Poussereau, S.; Journaux, Y.; Muñoz, M. C. J. Chem. Soc., Dalton Trans. 1998, 781–790. doi:10.1039/A706964B |
| 5. | Pardo, E.; Ruiz-García, R.; Cano, J.; Ottenwaelder, X.; Lescouëzec, R.; Journaux, Y.; Lloret, F.; Julve, M. Dalton Trans. 2008, 2780–2805. doi:10.1039/b801222a |
| 10. | Ruiz, R.; Surville-Barland, C.; Journaux, Y.; Colin, J. C.; Castro, I.; Cervera, B.; Julve, M.; Lloret, F.; Sapiña, F. Chem. Mater. 1997, 9, 201–209. doi:10.1021/cm9602961 |
| 11. | Sanada, T.; Suzuki, T.; Kaizaki, S. J. Chem. Soc., Dalton Trans. 1998, 959–966. doi:10.1039/A706834D |
| 25. | Cruickshank, D. W. J. Acta Crystallogr. 1949, 2, 65–82. doi:10.1107/S0365110X49000175 |
| 6. | Estrada, J.; Fernandez, I.; Pedro, J. R.; Ottenwaelder, X.; Ruiz, R.; Journaux, Y. Tetrahedron Lett. 1997, 38, 2377–2380. doi:10.1016/S0040-4039(97)00354-7 |
| 7. | Journaux, Y.; Ruiz, R.; Aukauloo, A.; Pei, Y. Mol. Cryst. Liq. Cryst. 1997, 305, 193–202. doi:10.1080/10587259708045056 |
| 8. | Ruiz, R.; Surville-Barland, C.; Aukauloo, A.; Anxolabehere-Mallart, E.; Journaux, Y.; Cano, J.; Muñoz, M. C. J. Chem. Soc., Dalton Trans. 1997, 745–752. doi:10.1039/A607572J |
| 9. | Ottenwaelder, X.; Aukauloo, A.; Journaux, Y.; Carrasco, R.; Cano, J.; Cervera, B.; Castro, I.; Curreli, S.; Muñoz, M. C.; Roselló, A. L.; Soto, B.; Ruiz-García, R. Dalton Trans. 2005, 2516–2526. doi:10.1039/b502478a |
| 23. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Kataev, V.; Rüffer, T. Dalton Trans. 2013, 42, 1798–1809. doi:10.1039/C2DT32259E |
| 5. | Pardo, E.; Ruiz-García, R.; Cano, J.; Ottenwaelder, X.; Lescouëzec, R.; Journaux, Y.; Lloret, F.; Julve, M. Dalton Trans. 2008, 2780–2805. doi:10.1039/b801222a |
| 9. | Ottenwaelder, X.; Aukauloo, A.; Journaux, Y.; Carrasco, R.; Cano, J.; Cervera, B.; Castro, I.; Curreli, S.; Muñoz, M. C.; Roselló, A. L.; Soto, B.; Ruiz-García, R. Dalton Trans. 2005, 2516–2526. doi:10.1039/b502478a |
| 11. | Sanada, T.; Suzuki, T.; Kaizaki, S. J. Chem. Soc., Dalton Trans. 1998, 959–966. doi:10.1039/A706834D |
| 14. | Rüffer, T.; Bräuer, B.; Powell, A. K.; Hewitt, I.; Salvan, G. Inorg. Chim. Acta 2007, 360, 3475–3483. doi:10.1016/j.ica.2007.03.037 |
| 15. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Zaripov, R.; Vavilova, E.; Voronkova, V.; Salikov, K.; Hahn, T.; Kortus, J.; Meva, F. E.; Schaarschmidt, D.; Rüffer, T. Dalton Trans. 2015, 44, 8062–8079. doi:10.1039/c4dt03579h |
| 16. | Rüffer, T.; Bräuer, B.; Meva, F. E.; Sorace, L. Inorg. Chim. Acta 2009, 362, 563–569. doi:10.1016/j.ica.2008.05.005 |
| 22. | Gao, E.-Q.; Zhao, Q.-H.; Tang, J.-K.; Liao, D.-Z.; Jiang, Z.-H.; Yan, S.-P. J. Chem. Soc., Dalton Trans. 2001, 1537–1540. doi:10.1039/B100142F |
| 19. | Pei, Y.; Journaux, Y.; Kahn, O. Inorg. Chem. 1988, 27, 399–404. doi:10.1021/ic00275a031 |
| 20. | Ribas, J.; Diaz, C.; Costa, R.; Journaux, Y.; Mathoniere, C.; Kahn, O.; Gleizes, A. Inorg. Chem. 1990, 29, 2042–2047. doi:10.1021/ic00336a003 |
| 21. | Wang, Q.-L.; Zhu, L.-N.; Liao, D.-Z.; Yan, S.-P.; Jiang, Z.-H.; Cheng, P.; Yang, G.-M. J. Mol. Struct. 2005, 754, 10–15. doi:10.1016/j.molstruc.2005.05.032 |
| 15. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Zaripov, R.; Vavilova, E.; Voronkova, V.; Salikov, K.; Hahn, T.; Kortus, J.; Meva, F. E.; Schaarschmidt, D.; Rüffer, T. Dalton Trans. 2015, 44, 8062–8079. doi:10.1039/c4dt03579h |
| 13. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Hahn, T.; Kortus, J.; Rüffer, T. Dalton Trans. 2012, 41, 14657–14670. doi:10.1039/c2dt31802d |
| 14. | Rüffer, T.; Bräuer, B.; Powell, A. K.; Hewitt, I.; Salvan, G. Inorg. Chim. Acta 2007, 360, 3475–3483. doi:10.1016/j.ica.2007.03.037 |
| 15. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Zaripov, R.; Vavilova, E.; Voronkova, V.; Salikov, K.; Hahn, T.; Kortus, J.; Meva, F. E.; Schaarschmidt, D.; Rüffer, T. Dalton Trans. 2015, 44, 8062–8079. doi:10.1039/c4dt03579h |
| 16. | Rüffer, T.; Bräuer, B.; Meva, F. E.; Sorace, L. Inorg. Chim. Acta 2009, 362, 563–569. doi:10.1016/j.ica.2008.05.005 |
| 17. | Abdulmalic, M. A.; Rüffer, T. Bull. Chem. Soc. Jpn. 2013, 86, 724–728. doi:10.1246/bcsj.20130031 |
| 18. | Abdulmalic, M. A. A Tailor-Made Approach for Thin Films and Monolayer Assemblies of bis (oxamato) and bis (oxamidato) Transition Metal Complexes. Ph.D. Thesis, Chemnitz University of Technology, Faculty of Natural Sciences, 2013. |
| 30. | Data collection, refinement and reduction software: CrysAlisPro, 1.171.38.41l ; Rigaku OD, 2015. |
| 1. | Kahn, O. Angew. Chem., Int. Ed. Engl. 1985, 24, 834–850. doi:10.1002/anie.198508341 |
| 11. | Sanada, T.; Suzuki, T.; Kaizaki, S. J. Chem. Soc., Dalton Trans. 1998, 959–966. doi:10.1039/A706834D |
| 15. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Zaripov, R.; Vavilova, E.; Voronkova, V.; Salikov, K.; Hahn, T.; Kortus, J.; Meva, F. E.; Schaarschmidt, D.; Rüffer, T. Dalton Trans. 2015, 44, 8062–8079. doi:10.1039/c4dt03579h |
| 9. | Ottenwaelder, X.; Aukauloo, A.; Journaux, Y.; Carrasco, R.; Cano, J.; Cervera, B.; Castro, I.; Curreli, S.; Muñoz, M. C.; Roselló, A. L.; Soto, B.; Ruiz-García, R. Dalton Trans. 2005, 2516–2526. doi:10.1039/b502478a |
| 24. | Cervera, B.; Sanz, J. L.; Ibáñez, M. J.; Vila, G.; Lloret, F.; Julve, M.; Ruiz, R.; Ottenwaelder, X.; Aukauloo, A.; Poussereau, S.; Journaux, Y.; Muñoz, M. C. J. Chem. Soc., Dalton Trans. 1998, 781–790. doi:10.1039/A706964B |
| 16. | Rüffer, T.; Bräuer, B.; Meva, F. E.; Sorace, L. Inorg. Chim. Acta 2009, 362, 563–569. doi:10.1016/j.ica.2008.05.005 |
| 13. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Hahn, T.; Kortus, J.; Rüffer, T. Dalton Trans. 2012, 41, 14657–14670. doi:10.1039/c2dt31802d |
| 15. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Zaripov, R.; Vavilova, E.; Voronkova, V.; Salikov, K.; Hahn, T.; Kortus, J.; Meva, F. E.; Schaarschmidt, D.; Rüffer, T. Dalton Trans. 2015, 44, 8062–8079. doi:10.1039/c4dt03579h |
| 27. | Krupskaya, Y.; Alfonsov, A.; Parameswaran, A.; Kataev, V.; Klingeler, R.; Steinfeld, G.; Beyer, N.; Gressenbuch, M.; Kersting, B.; Büchner, B. ChemPhysChem 2010, 11, 1961–1970. doi:10.1002/cphc.200900935 |
| 15. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Zaripov, R.; Vavilova, E.; Voronkova, V.; Salikov, K.; Hahn, T.; Kortus, J.; Meva, F. E.; Schaarschmidt, D.; Rüffer, T. Dalton Trans. 2015, 44, 8062–8079. doi:10.1039/c4dt03579h |
| 14. | Rüffer, T.; Bräuer, B.; Powell, A. K.; Hewitt, I.; Salvan, G. Inorg. Chim. Acta 2007, 360, 3475–3483. doi:10.1016/j.ica.2007.03.037 |
| 13. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Hahn, T.; Kortus, J.; Rüffer, T. Dalton Trans. 2012, 41, 14657–14670. doi:10.1039/c2dt31802d |
| 13. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Hahn, T.; Kortus, J.; Rüffer, T. Dalton Trans. 2012, 41, 14657–14670. doi:10.1039/c2dt31802d |
| 26. | Addison, A. W.; Rao, T. N.; Reedijk, J.; van Rijn, J.; Verschoor, G. C. J. Chem. Soc., Dalton Trans. 1984, 1349–1356. doi:10.1039/DT9840001349 |
| 13. | Abdulmalic, M. A.; Aliabadi, A.; Petr, A.; Krupskaya, Y.; Kataev, V.; Büchner, B.; Hahn, T.; Kortus, J.; Rüffer, T. Dalton Trans. 2012, 41, 14657–14670. doi:10.1039/c2dt31802d |
© 2017 Abdulmalic et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Nanotechnology terms and conditions: (http://www.beilstein-journals.org/bjnano)