Abstract
Ring-whizzing was investigated by hybrid DFT methods in a number of polyene–Pt(diphosphinylethane) complexes. The polyenes included cyclopropenium+, cyclobutadiene, cyclopentadienyl+, hexafluorobenzene, cycloheptatrienyl+, cyclooctatetraene, octafluorooctatetraene, 6-radialene, pentalene, phenalenium+, naphthalene and octafluoronaphthalene. The HOMO of a d10 ML2 group (with b2 symmetry) interacting with the LUMO of the polyene was used as a model to explain the occurrence of minima and maxima on the potential energy surface.
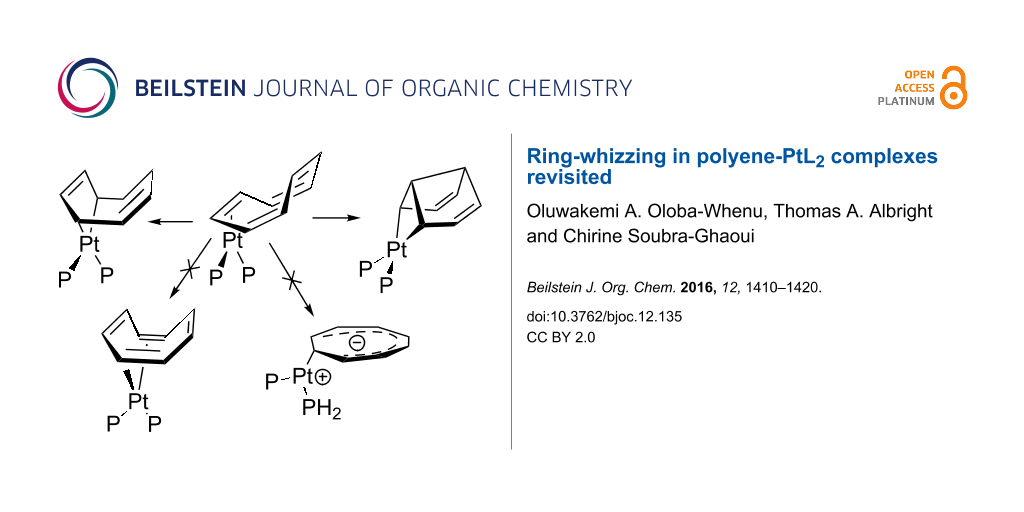
Graphical Abstract
Introduction
Polyene–transition metal complexes were found to undergo fluxional rearrangements as early as 1956 with the preparation of Cp2Fe(CO)2 [1]. The migration of an MLn unit around the periphery of a cyclic polyene is commonly called ring-whizzing, purportedly ascribed to Rowland Pettit [2]. A more inclusive term is haptotropic rearrangement [3] wherein a metal atom changes its hapticity along the reaction path. Haptotropic rearrangements in ML3 and MCp complexes are numerous [4-9] and have found use in synthetic strategies [10], switching devices [11-13] and energy storage [14,15]. Much less is known about the polyene–ML2 analogs. There are two classes of compounds; one set consists of d8 ML2 compounds [16-19] and the other, which we will be concerned with, are the d10 ML2 class. There is ample precedent for four basic coordination geometries exhibited by these compounds. These are shown in Figure 1. Notice that in each case the orientation of the ML2 unit is tied to the coordination number of the polyene and total electron count. One of us undertook a theoretical survey of these compounds at the extended Hückel level a number of years ago [20,21]. In the present contribution we shall revisit some of these rearrangements using DFT theory, as well as, investigate some new compounds.
Figure 1: The four coordination geometries for d10 polyene-ML2 complexes along with their hapto numbers and electron count.
Figure 1: The four coordination geometries for d10 polyene-ML2 complexes along with their hapto numbers and e...
A d10 ML2 fragment possesses a high-lying HOMO, shown by 5 in Figure 2, which has b2 symmetry and a low-lying LUMO, 6, of a1 symmetry [22]. An energetically favorable reaction path will be one that maximizes the interactions of these orbitals with the orbitals of a coordinated polyene. The lowest occupied polyene π level is fully symmetric and, therefore, 6 can always interact with it. On the other hand, the LUMO in the π system may not always have the correct symmetry to interact with the b2 orbital on ML2 and it is the evolution of this overlap that has an important impact on the reaction path and activation energy. We will also have an occasion to consider a lower lying filled orbital of b1 symmetry, 7.
![[1860-5397-12-135-2]](/bjoc/content/figures/1860-5397-12-135-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: The important valence orbitals of a d10 ML2 group, 5–7, along with the computed structures of Pt(PH3)2 and Pt(dpe).
Figure 2: The important valence orbitals of a d10 ML2 group, 5–7, along with the computed structures of Pt(PH3...
Polyene–ML2 complexes are very fragile which in turn makes it somewhat difficult to compute the reaction path. The bond dissociation energy for ethylene–Pt(PH3)2 is only about 17 kcal/mol [23]. There are two ways in which the metal–polyene bond can be strengthened. The electron affinity for C6F6 is much larger than that for benzene [24]. Consequently interaction of the filled b2 fragment orbital with the LUMO of C6F6 is expected to be larger and the binding energy larger than that for benzene. The M and L that we shall use in this work is Pt and a phosphine. The second method employs the use of a bidentate phosphine. In this regard we have chosen diphosphinylethane (dpe). This idea here is that the P–Pt–P angle is around 100° in polyene–ML2 complexes. Upon dissociation the 14 electron PtL2 complex strongly prefers to be linear [22]. So the computed ground state for Pt(PH3)2, shown in 8, is calculated to be 29 kcal/mol more stable than one where the P–Pt–P bond angle was constrained to be 99°. This of course is not the case for Pt(dpe), 9. The P–Pt–P angle remains at 98°. Thus, the bond dissociation energy in polyene–Pt(dpe) complexes rises along with the attendant barriers for haptotropic rearrangements. This has been analyzed and quantified in detail by Massera and Frenking [23] for olefin–ML2 compounds.
Computational Details
All geometries for the L = PH3 complexes were optimized without symmetry constraints within the DFT framework first using the B3LYP functional [25-27] in combination with the LANLDZ2 [28] basis sets. Single point calculations were carried out using the triple zeta d plus f polarization functions on Pt [29]. The geometry optimizations were then repeated using the M06 functional [30] along with the Def2-SV(P) basis set [31] for Pt, C, H and P except that the d functions on C were left off. Single point calculations used the Def2-TZVP basis [31] on Pt, P, C and H except for removing the f functions on C. F used a 6-31G basis [32] for the geometrical optimizations and 6-311G [33] in the single point calculations. Analytical frequencies were computed to determinate the nature of the stationary points. The Gaussian 09 software suite [34] was used in all of the calculations. The plots of the molecular structures utilized CYLview [35]. For brevity we will report the structures and Gibbs free energy differences in the standard state only for the polyene–Pt(dpe) complexes using frequencies from the Def2-SV(P) optimizations for the corrections to the Def2-TZVP energies. The geometries and total electronic energies are given as Supporting Information File 1.
Results and Discussion
A. Cyclic polyene–Pt(dpe) examples
The most simple of the cyclic polyenes is the cyclopropenium cation. Its LUMO is a degenerate par of π orbitals, labeled e”A and e”S in Figure 3. It is easy to see that e”A interacts with the b2 orbital of ML2 at an η2 geometry. Indeed this is the computed group state for C3H3–Pt(dpe)+ as shown from a side view, 10, in Figure 3. The transition state for shifting Pt(dpe) from one C–C bond to another passes through a geometry very close to η 3, as shown by 11. Here b2 interacts with e”S and along the reaction path a combination of the e” degenerate set. The essential features can be found elsewhere [21]. The Gibbs free energy difference between the two structures is small: 4.1 kcal/mol (2.4 kcal/mol for L = PH3). This is in accord with four structures of (Ph3C3)M(PPh3)2+ X− where M = Ni, Pd, and Pt and X− = ClO4 and PF6, which show a progressive movement of the ML2 unit over the face of the cyclopropenium ring [36]. These structures serve to chart this reaction path and this is consistent with a small reaction barrier with the resultant structure being determined by crystal packing effects. The details have been reported previously [21,36]. The optimizations reveal that the coordinated C–C bond is much longer, 1.62 Å, than the other two, 1.38 Å. This compares favorably to the M = Pt, X− = PF6 structure [37] where the C–C distances are 1.58(2) and 1.39 Å, respectively.
![[1860-5397-12-135-3]](/bjoc/content/figures/1860-5397-12-135-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: The empty degenerate set of π orbitals in the cyclopropenium cation is shown on the left side. On the right are the two optimized structures of C3H3–Pt(dpe)+.
Figure 3: The empty degenerate set of π orbitals in the cyclopropenium cation is shown on the left side. On t...
The situation for Cp–Pt(dpe)+ is very similar to the cyclopropenium case. Counting this as Cp+ means that there are two unoccupied orbitals that the b2 HOMO on ML2 can interact with. Each is one member of a degenerate set and they are shown on the left side of Figure 4. The two stationary points on the potential energy surface are displayed from a top view on the right side of Figure 4. The e”2 fragment orbital can interact with b2 to form an η3 complex as shown in 13. An η5 geometry, 14, will be favored using the empty e”1 orbital. The computed Gibbs free energy difference between the two is very small, namely 1.5 kcal/mol favoring η3. A recent search of the Cambridge crystallographic database [38] reveals 29 structures of the Cp- and indenyl-M(PR3)2+ type where M = Ni, Pd, Pt. For the more general CpML2 case where M = Fe through Pt there are 1074 hits. The majority of these structures are close to the η5 type although most have a significant range of M–C bond distances. For example, in cyclopentadienyl-platinum-bis(diphenylphosphinobiphenyl) [39] there are two Pt–C distances at 2.26(1) Å and one at 2.33(1) Å. The conformation of the PtL2 unit with respect to the Cp ring is approximately that given by 13. Accordingly, the remaining two Pt–C distances are 2.37(1) Å. For optimized 13 the corresponding set of distances is 2.29, 2.34 and 2.45 Å, respectively. The indenyl-M(PR3)2+ examples are decidedly η3 as a consequence of the perturbation generated by the benzo substituent. Normally one would do the electron counting in these molecules as Cp− and d8 ML2 yielding an 18-electron complex. The b2 fragment orbital is now formally empty and the e”1 set is filled. A full discussion of the bonding in these compounds may be found elsewhere [22].
![[1860-5397-12-135-4]](/bjoc/content/figures/1860-5397-12-135-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: Two unoccupied MOs for Cp+ are shown on the left side. The two stationary points for Cp–Pt(dpe)+ are given by 13 and 14. To conserve space the groups around the phosphorus atoms have been removed.
Figure 4: Two unoccupied MOs for Cp+ are shown on the left side. The two stationary points for Cp–Pt(dpe)+ ar...
Another polyene with two coordination geometries is cyclobutadiene. The eg set shown on the left side of Figure 5 is half-filled. It is easy to see that one member has the correct symmetry to interact with b2 ML2 at both the η2 and η4 geometries. We found for cyclobutadiene–Pt(dpe) that the η2 geometry, 15, is 6.5 kcal/mol more stable than the η4 geometry, 16. For L = PH3 the energy difference is even larger, 10.5 kcal/mol. These results are a little surprising in that the energy difference is larger than what we expected. We are aware of only one structure at this electron count, Ph4C4–Ni(PEt3)2 [40], and it is clearly η4. As we shall see later, the difference between Ni and Pt can be significant but for the time being, experiment and theory are not in agreement with each other.
![[1860-5397-12-135-5]](/bjoc/content/figures/1860-5397-12-135-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: The half-filled degenerate π orbitals in cyclobutadiene. The computed ground state (15) and transition state (16) for cyclobutadiene–Pt(dpe) on the right.
Figure 5: The half-filled degenerate π orbitals in cyclobutadiene. The computed ground state (15) and transit...
Benzene–Ni(PR3)2 compounds have been known for some time [41]. An η2 geometry has been observed to be the precursor to C–F bond insertion for F6C6 complexes [42] and a number of theoretical studies have been carried out [43-46] which address this reaction. There are two arene–Pt(PR3)2 structures in the literature [47,48] and both have η2 geometries. The barrier for ring whizzing in (CF3)6C6–Pt(PEt3)2 has been measured to be ≈11 kcal/mol [41]. One member of the LUMO e1g set in benzene has a large overlap with the b2 ML2 MO. The computed ground state structure for η2 F6C6–Pt(dpe), 17 in Figure 6 agrees well with the experiment. The issue is whether the transition state for ring whizzing favors the interaction between e1g and b2 shown from a top view in 18 or 19. Extended Hückel calculations favored the former [20,21]. Our present day calculations, however, favor 19. The structure is shown in 20. Special care was taken to search for a transition state where the Pt(dpe) group was rotated by 90° but none was found. The activation barrier was computed to be 7.4 kcal/mol. Reinhold, McGrady and Perutz [46] obtained a barrier of 6.4 kcal/mol for the same molecule using the B3LYP hybrid functional and a different basis set. The computed geometric parameters for the molecules are very close to each other. One Pt–C bond is short (2.10 Å) while the other two flanking bonds are 2.52 Å. Thus, 20 strongly resembles an η1 14 electron complex with a “T” shaped geometry. An easy way to view these results is to take a linear combination of b2 (5) and a1 (6). This will generate two equivalent dsp hybrids. One will be filled and can interact with one component of the e1g LUMO, 21, in Figure 6 and the other will remain empty, 22.
![[1860-5397-12-135-6]](/bjoc/content/figures/1860-5397-12-135-6.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: The ground and transition state for ring whizzing in F6C6–Pt(dpe), 17 and 20, respectively. The dominant bonding interaction for two possible transition states, 18 and 19 along with the HOMO, 21 and LUMO, 22, in the η1 transition state.
Figure 6: The ground and transition state for ring whizzing in F6C6–Pt(dpe), 17 and 20, respectively. The dom...
Another highly fluxional molecule is cycloheptatrienyl–Pt(dpe)+ which exhibits a situation similar to that described for Cp–Pt(dpe)+. The ground state is again an η3 structure. This is in agreement with several substituted cyclohepatrieneyl–PdL2 complexes [49]. We looked hard for an η5 species but instead found an η2 structure which serves as a transition state for ring whizzing. The activation barrier was computed to be 3.2 kcal/mol. Barriers from 10.5 to 7.6 kcal/mol were found for the Pd complexes [49]. Interestingly an η1 transition structure with one imaginary frequency was also discovered. It was found to be 7.2 kcal/mol above the ground state.
We thought that radialenes would be an attractive candidate as a ligand and would exhibit a facile haptotropic rearrangement when coordinated to Pt(dpe). The LUMO is all-in phase combination of olefinic π* as shown for 6-radialene by 23 in Figure 7. Therefore, the ML2 b2 fragment would retain a sizable portion of its overlap on going from an η2 to η4 geometry. For some time 6-radialene and many alkyl derivatives have been known [50]. It is extraordinarily reactive and a bis-Fe(CO)3 derivative of 5-radialene has recently been prepared [51]. The structure of 6-radialene is strongly distorted into a chair form with a boat conformation slightly higher in energy [51]. The D6h structure lies higher in energy by 17.1 kcal/mol [51]. Our optimization of the η2 ground state shows a twisted boat conformation to be the most stable, 24, in Figure 7. The activation barrier was found to be 13.7 kcal/mol. We thought that by tying the ends of the olefins together via a CH2 group would force the ligand to be flat. In fact there are compounds analogous to this having O, S and Se as the linker that are in fact flat [52]. Our calculations reveal that the η2 ground state, 25, and the η4 transition state, 26, are essentially flat, but the energy difference is only lowered to 13.0 kcal/mol. In 25 the two Pt–C bond distances are 2.17 Å, however, in 26 they are considerably lengthened. The inner Pt–C distances are 2.36 Å and the ones adjacent to the CH2 group are 2.61 Å! The principal destabilization in 26 is due to the interaction between b1 (7) and the HOMO on 6-radialene, which is the totally antibonding combination of π orbitals, 27.
![[1860-5397-12-135-7]](/bjoc/content/figures/1860-5397-12-135-7.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 7: The LUMO, 23, and HOMO, 27, in 6-radialene. The optimized η2 ground states are shown in 24 and 25 while 26 shows the geometry for one η4 transition state.
Figure 7: The LUMO, 23, and HOMO, 27, in 6-radialene. The optimized η2 ground states are shown in 24 and 25 w...
B. The strange case of cyclooctatetraene
Cyclooctatetraene (COT) has been a favorite ligand since the dawn of organometallic chemistry [2]. Figure 8 shows two representations for the half-filled e2u set of π orbitals in the flat D8h geometry. One can see from the representation in a) that an η2 or η4 conformation are possibilities. In b) one can envision η1 or η3 as potential structures. The optimized structures for C8F8–Pt(dpe) are illustrated in Figure 9. To conserve space the groups around the phosphorus atoms have been removed. COT and C8F8 have a tub shaped structure with D2d symmetry [53,54]. As expected an η2 structure, 28, was found to be a minimum. A 1,4-diyl minimum was also found where there are two Pt–C σ bonds, 30. This structure has also been suggested by means of the low temperature 31P and 13C NMR of COT-Pt(R2PCH2CH2PR2), R = iPr [55]. The transition state that interconnects 28 to 30 is shown in 29. The coordination geometry around Pt is typical of that in η2 olefin complexes. What is novel is that the COT (and C8F8) ring is essentially flat with the uncoordinated portion of the polyene having alternating C–C bond lengths of ≈1.45 and 1.35 Å. This is in fact the structure of an analogous Ni complex as determined by X-ray crystallography [56]. The haptotropic rearrangement of 28 to 30 does not permute all of the carbon atoms in the COT ring. There is a mirror plane in the plane of the paper for all of the structures in Figure 9. This equivalences the carbons on the front side of the paper with those on the back side. Compounds 28–30 do not have a mirror plane perpendicular to this and, therefore, C2 (see 28) does not become equivalent to C3, etc. As we shall see, a structure akin to 35 would accomplish this. In searching for another structure that accomplishes this we discovered tricyclic 32. The transition state that converts 28 into 32 is 31. For the C8F8 complex, 28, the Pt–C distances are 2.08 Å. In 31 the corresponding distances are 2.11 and 2.26 Å with the dashed green bond being formed measuring at 2.32 Å. In COT–Pt(dpe) the transition state 31 is akin to an η3 complex with the three Pt–C bond lengths calculated to be 2.22–2.26 Å. Since 32 has Cs symmetry (discounting the dpe ligand), it serves as a way-point for ring-whizzing. It is easy to see the electronic basis for ring folding and construction of the tricyclic molecule. Consider that in 28 the filled ML2 b2 orbital coordinates to the two lower p AOs in the upper component of e2u in Figure 8a. Then empty a1 interacts with the lower component in Figure 8a. As ML2 slips over the polyene in a clockwise motion the appropriate e2u representations become those in Figure 8b. The empty orbital at the top right in Figure 8 interacts with the filled b2 ML2 orbital and a1 interacts with the filled e2u. This is explicitly drawn in 33 and 34, respectively, of Figure 10. The important consequence of this motion is that the p AO on the opposite side of the ring in 34 has the correct phase to generate a C–C σ bond and this collapses to bicyclic 32.
![[1860-5397-12-135-8]](/bjoc/content/figures/1860-5397-12-135-8.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 8: Two representations for the half-filled e2u set of π orbitals in cyclooctatetraene.
Figure 8: Two representations for the half-filled e2u set of π orbitals in cyclooctatetraene.
![[1860-5397-12-135-9]](/bjoc/content/figures/1860-5397-12-135-9.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 9: The stationary points found on the potential energy surface of C8F8–Pt(dpe). For clarity the groups around the phosphines have been removed. The relative energies for this compound, as well as COT–Pt(dpe) are given below each structure.
Figure 9: The stationary points found on the potential energy surface of C8F8–Pt(dpe). For clarity the groups...
![[1860-5397-12-135-10]](/bjoc/content/figures/1860-5397-12-135-10.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 10: The two important bonding interactions for transition state 31 are drawn in 33 and 34.
Figure 10: The two important bonding interactions for transition state 31 are drawn in 33 and 34.
Our calculations find that C8F8–Pt(dpe) will be caught in the deep potential energy well of the tricyclic isomer, 32. Hughes and co-workers have shown that experimentally this is indeed the case [57,58]. With PPh3 and AsPh3 ligands compounds analogous to 30 are initially formed from the reaction of C8F8 and a Pt(0) precursor. 30 then irreversibly rearranges in solution to 32 overnight at room temperature. This is also in accord with our calculations. Notice that going from 30 to 32 requires the passage through transition state 29, which requires 29 kcal/mol. We think that the reason why 29 lies much higher in energy than the COT analog is due to the energy cost associated with flattening the ligand to a D4h type of geometry. For COT itself this entails an energy cost of 10–13 kcal/mol [59]. We find that the conversion for C8F8 is nearly triple this amount, namely 29.9 kcal/mol [60].
The picture for COT–Pt(dpe) is not so clear. Our calculations would have 28, 30 and 32 in rapid equilibrium with the overwhelming majority of the equilibrium shifted to the tricyclic compound. The low temperature 31P and 13C NMR of COT–Pt(R2PCH2CH2PR2), R = iPr [55], clearly shows that either 28 or 31 (the authors prefer 31) is in rapid equilibrium with 30. There is no spectroscopic evidence consistent with the existence of 32. It may well be the case that bulky iPr groups in place of hydrogens alter the relative energetics. Perhaps computations with a different functional and/or a larger basis set might bring theory and experiment into agreement. Furthermore, moving from Pt to the isoelectronic Ni also can have a significant impact. An X-ray of the COT–Ni complex [56] reveals the structure is analogous to that for 29. An X-ray of another Ni complex [60] produces a bis-η2 isomer, 35. This is also true for C8F8–Ni complexes with certain ligand sets [57,58]. We carried out a number of potential energy minimizations as shown in Figure 11 starting from 35, as well as, η1, 36, and η3, 37. Unfortunately none of these produced new stationary points. We will return to this Ni versus Pt issue later.
![[1860-5397-12-135-11]](/bjoc/content/figures/1860-5397-12-135-11.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 11: Three other coordination geometries that did not lead to new stationary points are shown in 35–37.
Figure 11: Three other coordination geometries that did not lead to new stationary points are shown in 35–37.
C. Polycyclic examples
Pentalene metal complexes have been the subject of a number of investigations [61], as well as, theoretical explorations of haptotropic rearrangements with ML3 and MCp [62,63]. However, we are not aware of any complexes with a d10 ML2 group. Pentalene has an energetically low-lying LUMO and close to it another empty orbital. These are shown in 38 and 39, respectively, in Figure 12. It is easy to see that in 38 the b2 ML2 fragment orbital can interact in an η3 mode both within the five-membered ring, as well as, between the two. 39 has the correct topology to interact with b2 in η2 and η3 modes. We were able to locate four stationary points on the potential energy surface of pentalene–Pt(dpe). These are shown from a top view along with their relative energies in Figure 12. Here again the hydrogens and ethano-bridge connected to the phosphorus atoms has been removed for clarity. We find that the η2 structure, 40, to be the ground state. A low energy η3 transition state, 41, at 7.7 kcal/mol serves to equivalence the top and bottom halves of the pentalene ligand. The Pt(dpe) group can migrate from one ring to the other via the η3 structure, 42. Again the activation energy associated with the transition state 43 is predicted to be small at 8.6 kcal/mol. We anticipate that pentalene–Pt(PR3)2 will be a highly fluxional molecule.
![[1860-5397-12-135-12]](/bjoc/content/figures/1860-5397-12-135-12.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 12: The LUMO and LUMO+1 shown in 38 and 39, respectively. The four stationary points found for pentalene–Pt(dpe) are displayed in 40–43 along with their relative energies. The groups connected to the phosphorus atoms are not shown.
Figure 12: The LUMO and LUMO+1 shown in 38 and 39, respectively. The four stationary points found for pentalen...
The situation for phenalenium–Pt(dpe)+ is very similar. The LUMO for phenalenium+ is a rigorously non-bonding MO, 44 in Figure 13. One expects and finds η3 structures both within and between rings as given by 45 and 46, respectively, with essentially identical relative energies. Experimentally, all known complexes [64-67] are akin to 45. Our calculated barrier of 14.7 kcal/mol via 47 seems a bit too low. The measured barrier in two Pd(tmeda) complexes was 21.4 and 21.6 kcal/mol [66]. No signs of fluxionality was found in a substituted phenalenium–Pt(PPh3)2+ complex [67].
![[1860-5397-12-135-13]](/bjoc/content/figures/1860-5397-12-135-13.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 13: The LUMO of the phenalenium cation is given in 44. The structures of the three stationary points found for phenalenium–Pt(dpe)+ along with their relative energies are shown from a top view in 45–47. Again the groups connected to the phosphorus atoms are not shown.
Figure 13: The LUMO of the phenalenium cation is given in 44. The structures of the three stationary points fo...
Naphthalene and anthracene–Ni(PR3)2 compounds have been known and studied for some time [45,46,68-75]. We are, however, unaware of any Pt(PR3)2 examples. The ground state structures of the Ni compounds possess an η2 geometry where the Ni is coordinated to a carbon–carbon bond adjacent to the ring fusion. Our calculations on octafluoronaphthalene–Ni(dpe) and –Pt(dpe) (as well as naphthalene–Pt(dpe) itself) are in good agreement with experiment. A top view of the structure is shown by 48 in Figure 14. This offers a good overlap between the LUMO in C10F8, 49, and the b2 HOMO, 5, in Pt(dpe). It was thought [20] that migration of an ML2 unit from one ring to another would involve an η3 structure where Pt would bond to C(1), C(9) and C(8). For the carbon numbering system please see 48. Bonding between b2 ML2 and the b1g MO would be retained. Unfortunately this is not quite the entire story. One of the stationary points is shown by 50. The au HOMO, 51, in C10F8 also has a significant overlap with b2 at this geometry. Since these two fragment orbitals are both filled, there is also considerable destabilization. What we find is that this expanse of the potential energy surface is a twixtyl intermediate [76]. At the stationary point given by 50 there is one imaginary frequency of 17i cm−1; at another closer to η3 the computed frequencies are all positive but one is tiny, 15 cm−1. So this region of the coordinate space is analogous to a plateau; the potential energy is essentially flat. The activation energy to attain 50 in C10F8–Pt(dpe) was computed to be 13.7 kcal/mol; in C10H8–Pt(dpe) the barrier was 14.8 kcal/mol. This is in line with an NMR derived barrier of about 15 kcal/mol for C10H8NiL2 [74] and 15–20 kcal/mol for anthracene–Ni(PR3)2 [69,70]. Oprunenko and Gloriozov [75] have calculated the η3 tranisition state to lie at a relative energy of 12.2 kcal/mol for naphthalene–Ni(PEt3)2 using the PBE functional and a different basis set than that employed here. Jones and co-workers [45] have undertaken an exhaustive study of ring whizzing and oxidative addition in a series of cyano and methyl substituted naphthalene–Ni(dmpe) complexes at the B3LYP level. Structures analogous to 50 were reported at relative energies of 12–17.5 kcal/mol. We do find in C10F8–Pt(dpe) that there is a second path for the haptotropic rearrangement from one ring to the other. Here the Pt(dpe) group migrates further in towards the ring junction with a weakly bound transition state of 21.9 kcal/mol and ending at an η2 minimium where the C(9) and C(10) atoms are coordinated to Pt at a relative energy of 17.9 kcal/mol. The latter structures were also computed to lie at high energies by Jones and co-workers [45]. So, at this point theory and experiment appear to be in agreement for the NiL2 and PtL2 cases.
![[1860-5397-12-135-14]](/bjoc/content/figures/1860-5397-12-135-14.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 14: A top view of two stationary points found for F8C10–Pt(dpe); 48 is the ground state and 50, represents one point on the plateau. The LUMO and HOMO in naphthalene are drawn in 49 and 51, respectively.
Figure 14: A top view of two stationary points found for F8C10–Pt(dpe); 48 is the ground state and 50, represe...
But the story does not end here. Experimentally there is a low energy process that converts, 48, to the equivalent η2 complex where the ML2 group is coordinated to C(3) and C(4). This is also the case for anthracene–NiL2. The experimental barriers range ≈5–6 kcal/mol [69,70,74]. The aforementioned calculations [45,75] yield barriers of 4.2–9.5 kcal/mol in reasonable agreement with the experiment. The structures of these transition states resemble η4 species with the geometry akin to 52 in Figure 15. This is not the case for C10F8–Pt(dpe) or C10H8–Pt(dpe). The barriers are calculated to be 17.1 and 17.4 kcal/mol, respectively. Furthermore, the barrier for C10H8–Pt(dpe) using the B3LYP function generates a barrier of 17.8 kcal/mol. Using the M06 functional for C10F8–Ni(dpe) yields a barrier of 6.1 kcal/mol which is in line with the calculations by others. Therefore, the discrepancy must lie in the difference between Pt and Ni. There is also a difference in the metrical details of these transition states. For the Ni examples the Ni–C(1) and Ni–C(4) distances are ≈0.3 Å longer than the Ni–C(2) and Ni–(3) ones (see 48 for the numbering scheme). For the Pt complexes we find this difference to be about twice as large. In other words, the Pt cases are closer to η2 complexes where the olefinic portion of the ligand is rotated by 90° from the minimum energy conformation given in 1. We will return to this point shortly. One might think that the overlap between b2 ML2 and the LUMO, 49, from the η2 ground state to η4 will be retained and, thus, the activation energy will be small. However, note that at η4 the overlap between the filled b1 fragment orbital, 7, and the au HOMO on C10F8 is turned on and this is repulsive. With this in mind it is tempting to put forward the hypothesis that the 3d AOs in Ni are very contracted and their overlap at 52 is not so large. Hence the au – b1 repulsion is not so large and it is the mixing of 4p character in the Ni b2 orbital that retains reasonable overlap with b1g. On the other hand, the Pt 5d AO is more diffuse and consequently more bonding is lost at η4 than its Ni congener. But this cannot be the whole story. Massera and Frenking [23] have shown that there is essentially no energy difference between the bond dissociation energy (BDE) in ethylene–Ni(dpe) and the Pt analog. Furthermore, their calculated BDE for ethylene–Pt(PH3)2 is in very good agreement with that found [23] at the CCSD(T) level with a large basis set. On the other hand, Reinhold, McGrady and Perutz have reported [46] that C6H6 and C6F6–Pt(dpe) BDEs are about 8 kcal/mol less than that for the Ni(dpe) analogs.
![[1860-5397-12-135-15]](/bjoc/content/figures/1860-5397-12-135-15.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 15: At top view of the η4, 52, and η4, 54, transition states along with the η2, 53, intermediate.
Figure 15: At top view of the η4, 52, and η4, 54, transition states along with the η2, 53, intermediate.
A close examination of the potential energy surface in C10F8–Pt(dpe) revealed the existence of another η2 minimum, 53, in Figure 15. It lies 13.7 kcal/mol above the ground state. This is in line with the corresponding minima found by Jones and co-workers [45] in the substituted naphthalene–Ni(dmpe) compounds (≈13 kcal/mol). So our calculations put the η2 minimum, 53, to be 3.4 kcal/mol more stable than the η4 transition state, 52. However, the latter does not serve as the waypoint for the former. An η1 structure, 54, was found to be the transition state for the haptotropic rearrangement of 48 to 53. Notice that passage through the η2 intermediate causes the phosphines to become equivalent. Benn and co-workers [74] in fact observe phosphine equivalence with a barrier of approximately 13 kcal/mol for the naphthalene–Ni(PR3)2 compounds. Our calculations put 54 to be 14.9 kcal/mol above the ground state, 48. This is in reasonable agreement with the NMR results [74]. The reaction path and associated electronic details for the 48 to 54 to 53 haptotropic shift is precisely analogous to ring-whizzing in C6F6–Pt(dpe) that was covered previously. In summary we find the potential energy surface for naphthalene–Pt and –Ni complexes to be quite different. In C10F8–Pt(dpe), haptotropic rearrangement from one ring to another is energetically similar to that within one ring, whereas, in the Ni analog the former is much slower than the latter.
Conclusion
Our original thesis that the ML2 b2 interaction with the LUMO of the polyene dictated the reaction path was largely fulfilled. Often this guided our exploration of the potential energy surfaces. But molecules, like life, sometimes yield unexpected conclusions. We miss you, Peter Hofmann.
Supporting Information
| Supporting Information File 1:
The molecular geometry and total electronic energy for the molecules in this work are given in .xyz format. The file may be opened as a text file to read the coordinates, or opened directly by a molecular modeling program such as Mercury (http://www.ccdc.cam.ac.uk/pages/Home.aspx).
Molecular geometry and total electronic energy data. |
||
| Format: XYZ | Size: 60.6 KB | Download |
References
-
Piper, T. S.; Wilkinson, G. J. Inorg. Nucl. Chem. 1956, 3, 104. doi:10.1016/0022-1902(56)80073-0
Return to citation in text: [1] -
Cotton, F. A. Inorg. Chem. 2002, 41, 643. doi:10.1021/ic010972n
and references therein.
Return to citation in text: [1] [2] -
Anh, N. T.; Elian, M.; Hoffmann, R. J. Am. Chem. Soc. 1978, 100, 110. doi:10.1021/ja00469a019
Return to citation in text: [1] -
Gloriozov, I. P.; Marchal, R.; Saillard, J.-Y.; Oprunenko, Y. F. Eur. J. Inorg. Chem. 2015, 250. doi:10.1002/ejic.201402879
Return to citation in text: [1] -
Jiménez-Halla, J. O. C.; Robles, J.; Solá, M. Organometallics 2008, 27, 5230. doi:10.1021/om800505j
Return to citation in text: [1] -
Czerwinski, C. J.; Fetisov, E. O.; Gloriozov, I. P.; Oprunenko, Y. F. Dalton Trans. 2013, 42, 10487. doi:10.1039/c3dt50655j
Return to citation in text: [1] -
Fetisov, E. O.; Gloriozov, I. P.; Oprunenko, Yu. F.; Saillard, J.-Y.; Kahlal, S. Organometallics 2013, 32, 3512. doi:10.1021/om4003335
Return to citation in text: [1] -
Gridnev, I. D. Coord. Chem. Rev. 2008, 252, 1798. doi:10.1016/j.ccr.2007.10.021
Return to citation in text: [1] -
Oprunenko, Yu. F. Russ. Chem. Rev. 2000, 69, 683. doi:10.1070/RC2000v069n08ABEH000589
Return to citation in text: [1] -
Kündig, E. P.; Pape, A. Top. Organomet. Chem. 2004, 7, 71. doi:10.1007/b12823
Return to citation in text: [1] -
Hülsen, M.; Norman, P.; Dolg, M. J. Organomet. Chem. 2011, 696, 3861. doi:10.1016/j.jorganchem.2011.08.039
Return to citation in text: [1] -
Nakai, H.; Isobe, K. Coord. Chem. Rev. 2010, 254, 2652. doi:10.1016/j.ccr.2009.12.025
Return to citation in text: [1] -
Dötz, K. H.; Jahr, H. C. Chem. Rec. 2004, 4, 61. doi:10.1002/tcr.20007
Return to citation in text: [1] -
Albright, T. A.; Dosa, P. I.; Grossmann, T. N.; Khrustalev, V. N.; Oloba, O. A.; Padilla, R.; Paubelle, R.; Stanger, A.; Timofeeva, T. V.; Vollhardt, K. P. C. Angew. Chem., Int. Ed. 2009, 48, 9853. doi:10.1002/anie.200905088
Return to citation in text: [1] -
Albright, T. A.; Drissi, R.; Gandon, V.; Oldenhof, S.; Oloba-Whenu, O. A.; Padilla, R.; Shen, H.; Vollhardt, K. P. C.; Vreeken, V. Chem. – Eur. J. 2015, 21, 4546. doi:10.1002/chem.201406211
Return to citation in text: [1] -
Crabtree, R. H.; Parnell, C. P. Organometallics 1984, 3, 1727. doi:10.1021/om00089a022
Return to citation in text: [1] -
Woolf, A.; Chaplin, A. B.; McGrady, J. E.; Alibadi, M. A. M.; Rees, N.; Draper, S.; Murphy, F.; Weller, A. S. Eur. J. Inorg. Chem. 2011, 1614. doi:10.1002/ejic.201001263
Return to citation in text: [1] -
Woolf, A.; Alibadi, M. A. M.; Chaplin, A. B.; McGrady, J. E.; Weller, A. S. Eur. J. Inorg. Chem. 2011, 1626. doi:10.1002/ejic.201001264
Return to citation in text: [1] -
Oprunenko, Yu. F.; Gloriozov, I. P. Russ. Chem. Bull. 2010, 59, 2061. doi:10.1007/s11172-010-0355-1
Return to citation in text: [1] -
Silvestre, J.; Albright, T. A. J. Am. Chem. Soc. 1985, 107, 6829. doi:10.1021/ja00310a015
Return to citation in text: [1] [2] [3] -
Silvestre, J.; Albright, T. A. Nouv. J. Chim. 1985, 9659.
Return to citation in text: [1] [2] [3] [4] -
Albright, T. A.; Burdett, J.; Whangbo, M.-H. Orbital Interactions in Chemistry, 2nd ed.; Wiley: Hoboken, 2013; pp 537–544; 549–552. doi:10.1002/9781118558409
Return to citation in text: [1] [2] [3] -
Massera, C.; Frenking, G. Organometallics 2003, 22, 2758. doi:10.1021/om0301637
Return to citation in text: [1] [2] [3] [4] -
Voora, V. K.; Jordan, K. D. J. Phys. Chem. A 2014, 118, 7201. doi:10.1021/jp408386f
and references therein.
Return to citation in text: [1] -
Becke, A. D. J. Chem. Phys. 1993, 98, 5648. doi:10.1063/1.464913
Return to citation in text: [1] -
Stephens, P. J.; Devlin, F. J.; Chabalowski, C. F.; Frisch, M. J. J. Phys. Chem. 1994, 98, 11623. doi:10.1021/j100096a001
Return to citation in text: [1] -
Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785. doi:10.1103/PhysRevB.37.785
Return to citation in text: [1] -
Hay, J. R.; Wadt, W. R. J. Chem. Phys. 1985, 82, 299. doi:10.1063/1.448975
Return to citation in text: [1] -
Roy, L. E.; Hay, J. P.; Martin, R. L. J. Chem. Theory Comput. 2008, 4, 1029. doi:10.1021/ct8000409
Return to citation in text: [1] -
Zhao, Y.; Truhlar, D. G. Theor. Chem. Acc. 2008, 120, 215. doi:10.1007/s00214-007-0310-x
Return to citation in text: [1] -
Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys. 2005, 7, 3297. doi:10.1039/b508541a
Return to citation in text: [1] [2] -
Ditchfield, R.; Hehre, W. J.; Pople, J. A. J. Chem. Phys. 1971, 54, 724. doi:10.1063/1.1674902
Return to citation in text: [1] -
Krishnan, R.; Binkley, J. S.; Seeger, R.; Pople, J. A. J. Chem. Phys. 1980, 72, 650. doi:10.1063/1.438955
Return to citation in text: [1] -
Gaussian 09, Revision B.01; Gaussian, Inc.: Wallingford CT, 2010.
Return to citation in text: [1] -
CYLview, 1.0b; Legault, C. Y., Université de Sherbrooke, 2009, http://www.cylview.org.
Return to citation in text: [1] -
Mealli, C.; Midollini, S.; Moneti, S.; Sacconi, L.; Silvestre, J.; Albright, T. A. J. Am. Chem. Soc. 1982, 104, 95. doi:10.1021/ja00365a020
Return to citation in text: [1] [2] -
McClure, M. D.; Weaver, D. L. J. Organomet. Chem. 1973, 54, C59. doi:10.1016/S0022-328X(00)84983-9
Return to citation in text: [1] -
CSD version 5.37 (Nov.2015 plus 1 update).
Return to citation in text: [1] -
Becker, J. J.; White, P. S.; Gagné, M. R. J. Am. Chem. Soc. 2001, 123, 9478. doi:10.1021/ja016167p
Return to citation in text: [1] -
Eisch, J. J.; Piotrowski, A. M.; Aradi, A. A.; Krüger, C.; Romão, M. J. Z. Naturforsch., B 1985, 40, 624. doi:10.1515/znb-1985-0511
Return to citation in text: [1] -
Browning, J.; Green, M.; Penfold, B. R.; Spencer, J. L.; Stone, F. G. A. J. Chem. Soc., Chem. Commun. 1973, 31. doi:10.1039/c39730000031
Return to citation in text: [1] [2] -
Clot, E.; Eisenstein, O.; Jasim, N.; Macgregor, S. A.; McGrady, J. E.; Perutz, R. N. Acc. Chem. Res. 2011, 44, 333. doi:10.1021/ar100136x
see for a review.
Return to citation in text: [1] -
Hatnean, J. A.; Johnson, S. A. Organometallics 2012, 31, 1361. doi:10.1021/om200990g
Return to citation in text: [1] -
Johnson, S. A.; Mroz, N. M.; Valdizon, R.; Murray, S. Organometallics 2011, 30, 441. doi:10.1021/om100699d
Return to citation in text: [1] -
Li, T.; García, J. J.; Brennessel, W. W.; Jones, W. D. Organometallics 2010, 29, 2430. doi:10.1021/om100001m
Return to citation in text: [1] [2] [3] [4] [5] [6] -
Reinhold, M.; McGrady, J. E.; Perutz, R. N. J. Am. Chem. Soc. 2004, 126, 5268. doi:10.1021/ja0396908
Return to citation in text: [1] [2] [3] [4] -
Cobbledick, R. E.; Einstein, F. W. B. Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 1978, 34, 1849. doi:10.1107/S0567740878006822
Return to citation in text: [1] -
Browning, J.; Penfold, B. R. J. Cryst. Mol. Struct. 1974, 4, 335. doi:10.1007/BF01636047
Return to citation in text: [1] -
Jandl, C.; Öfele, K.; Kühn, F. E.; Herrmann, W. A.; Pöthig, A. Organometallics 2014, 33, 6398. doi:10.1021/om500738d
Return to citation in text: [1] [2] -
Barkovich, A. J.; Strauss, E. S.; Vollhardt, K. P. C. J. Am. Chem. Soc. 1977, 99, 8321. doi:10.1021/ja00467a036
Return to citation in text: [1] -
Mackay, E. G.; Newton, C. G.; Toombs-Ruane, H.; Lindeboom, E. J.; Fallon, T.; Willis, A. C.; Paddon-Row, M. N.; Sherburn, M. S. J. Am. Chem. Soc. 2015, 137, 14653. doi:10.1021/jacs.5b07445
Return to citation in text: [1] [2] [3] -
Fallon, T.; Willis, A. C.; Rae, A. D.; Paddon-Row, M. N.; Sherburn, M. S. Chem. Sci. 2012, 3, 2133. doi:10.1039/c2sc20130e
and references therein.
Return to citation in text: [1] -
Claus, K. H.; Krüger, C. Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 1988, C44, 1632. doi:10.1107/S0108270188005840
Return to citation in text: [1] -
Laird, B. B.; Davis, R. E. Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 1982, B38, 678. doi:10.1107/S0567740882003781
Return to citation in text: [1] -
Schager, F.; Haack, K.-J.; Mynott, R.; Rufińska, A.; Pörschke, K.-R. Organometallics 1998, 17, 807. doi:10.1021/om970762b
and references therein.
Return to citation in text: [1] [2] -
Bach, I.; Pörschke, K.-R.; Proft, B.; Goddard, R.; Kopiske, C.; Krüger, C.; Rufińska, A.; Seevogel, K. J. Am. Chem. Soc. 1997, 119, 3773. doi:10.1021/ja964210g
Return to citation in text: [1] [2] -
Carl, R. T.; Corcoran, E. W., Jr.; Hughes, R. P.; Samkoff, D. E. Organometallics 1990, 9, 838. doi:10.1021/om00117a046
Return to citation in text: [1] [2] -
Hughes, R. P. J. Fluorine Chem. 2010, 131, 1059. doi:10.1016/j.jfluchem.2010.06.014
Return to citation in text: [1] [2] -
Klärner, F.-G. Angew. Chem., Int. Ed. 2001, 40, 3977. doi:10.1002/1521-3773(20011105)40:21<3977::AID-ANIE3977>3.0.CO;2-N
and references therein.
Return to citation in text: [1] -
Sánchez-Sanz, G.; Trujillo, C.; Rozas, I.; Alkorta, I. Phys. Chem. Chem. Phys. 2015, 17, 14961. doi:10.1039/C5CP00876J
Return to citation in text: [1] [2] -
Summerscales, O. T.; Cloke, F. G. N. Coord. Chem. Rev. 2006, 250, 1122. doi:10.1016/j.ccr.2005.11.020
Return to citation in text: [1] -
Deramchi, K.; Maouche, B.; Kahlal, S.; Saillard, J.-Y. Inorg. Chim. Acta 2011, 370, 499. doi:10.1016/j.ica.2011.02.059
Return to citation in text: [1] -
Li, H.; Feng, H.; Sun, W.; Xie, Y.; King, R. B.; Schaefer, H. F., III. New J. Chem. 2011, 35, 1718. doi:10.1039/c1nj20144a
Return to citation in text: [1] -
Nakasuji, K.; Yamaguschi, M.; Murata, I.; Tatsumi, K.; Nakamura, A. Chem. Lett. 1983, 12, 1489. doi:10.1246/cl.1983.1489
Return to citation in text: [1] -
Nakasuji, K.; Yamaguschi, M.; Murata, I.; Tatsumi, K.; Nakamura, A. Organometallics 1984, 3, 1257. doi:10.1021/om00086a018
Return to citation in text: [1] -
Nakasuji, K.; Yamaguschi, M.; Murata, I.; Nakanishi, H. J. Am. Chem. Soc. 1986, 108, 325. doi:10.1021/ja00262a039
Return to citation in text: [1] [2] -
Keasey, A.; Bailey, P. M.; Maitlis, P. M. J. Chem. Soc., Chem. Commun. 1978, 142. doi:10.1039/C39780000142
Return to citation in text: [1] [2] -
Stanger, A. Organometallics 1991, 10, 2979. doi:10.1021/om00054a082
Return to citation in text: [1] -
Stanger, A.; Vollhardt, K. P. C. Organometallics 1992, 11, 317. doi:10.1021/om00037a054
Return to citation in text: [1] [2] [3] -
Stanger, A.; Weisman, H. J. Organomet. Chem. 1996, 515, 183. doi:10.1016/0022-328X(95)06104-5
Return to citation in text: [1] [2] [3] -
Braun, Y.; Cronin, L.; Higgitt, C. L.; McGrady, J. E.; Perutz, R. N.; Reinhold, M. New J. Chem. 2001, 25, 19. doi:10.1039/B006368L
Return to citation in text: [1] -
Hatnean, J. A.; Beck, R.; Borrelli, J. D.; Johnson, S. A. Organometallics 2010, 29, 6077. doi:10.1021/om1008499
Return to citation in text: [1] -
Schaub, T.; Fischer, P.; Steffen, A.; Braun, T.; Radius, U.; Mix, A. J. Am. Chem. Soc. 2008, 130, 9304. doi:10.1021/ja074640e
Return to citation in text: [1] -
Benn, R.; Mynott, R.; Topalovic, I.; Scott, F. Organometallics 1989, 8, 2299. doi:10.1021/om00112a002
Return to citation in text: [1] [2] [3] [4] [5] -
Oprunenko, Yu. F.; Gloriozov, I. P. Russ. Chem. Bull. 2011, 60, 213. doi:10.1007/s11172-011-0036-8
Return to citation in text: [1] [2] [3] -
Hoffmann, R.; Swaminathan, S.; Odell, B. G.; Gleiter, R. J. Am. Chem. Soc. 1970, 92, 7091. doi:10.1021/ja00727a013
Return to citation in text: [1]
| 37. | McClure, M. D.; Weaver, D. L. J. Organomet. Chem. 1973, 54, C59. doi:10.1016/S0022-328X(00)84983-9 |
| 23. | Massera, C.; Frenking, G. Organometallics 2003, 22, 2758. doi:10.1021/om0301637 |
| 39. | Becker, J. J.; White, P. S.; Gagné, M. R. J. Am. Chem. Soc. 2001, 123, 9478. doi:10.1021/ja016167p |
| 23. | Massera, C.; Frenking, G. Organometallics 2003, 22, 2758. doi:10.1021/om0301637 |
| 69. | Stanger, A.; Vollhardt, K. P. C. Organometallics 1992, 11, 317. doi:10.1021/om00037a054 |
| 70. | Stanger, A.; Weisman, H. J. Organomet. Chem. 1996, 515, 183. doi:10.1016/0022-328X(95)06104-5 |
| 74. | Benn, R.; Mynott, R.; Topalovic, I.; Scott, F. Organometallics 1989, 8, 2299. doi:10.1021/om00112a002 |
| 45. | Li, T.; García, J. J.; Brennessel, W. W.; Jones, W. D. Organometallics 2010, 29, 2430. doi:10.1021/om100001m |
| 75. | Oprunenko, Yu. F.; Gloriozov, I. P. Russ. Chem. Bull. 2011, 60, 213. doi:10.1007/s11172-011-0036-8 |
| 45. | Li, T.; García, J. J.; Brennessel, W. W.; Jones, W. D. Organometallics 2010, 29, 2430. doi:10.1021/om100001m |
| 41. | Browning, J.; Green, M.; Penfold, B. R.; Spencer, J. L.; Stone, F. G. A. J. Chem. Soc., Chem. Commun. 1973, 31. doi:10.1039/c39730000031 |
| 20. | Silvestre, J.; Albright, T. A. J. Am. Chem. Soc. 1985, 107, 6829. doi:10.1021/ja00310a015 |
| 21. | Silvestre, J.; Albright, T. A. Nouv. J. Chim. 1985, 9659. |
| 43. | Hatnean, J. A.; Johnson, S. A. Organometallics 2012, 31, 1361. doi:10.1021/om200990g |
| 44. | Johnson, S. A.; Mroz, N. M.; Valdizon, R.; Murray, S. Organometallics 2011, 30, 441. doi:10.1021/om100699d |
| 45. | Li, T.; García, J. J.; Brennessel, W. W.; Jones, W. D. Organometallics 2010, 29, 2430. doi:10.1021/om100001m |
| 46. | Reinhold, M.; McGrady, J. E.; Perutz, R. N. J. Am. Chem. Soc. 2004, 126, 5268. doi:10.1021/ja0396908 |
| 47. | Cobbledick, R. E.; Einstein, F. W. B. Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 1978, 34, 1849. doi:10.1107/S0567740878006822 |
| 48. | Browning, J.; Penfold, B. R. J. Cryst. Mol. Struct. 1974, 4, 335. doi:10.1007/BF01636047 |
| 41. | Browning, J.; Green, M.; Penfold, B. R.; Spencer, J. L.; Stone, F. G. A. J. Chem. Soc., Chem. Commun. 1973, 31. doi:10.1039/c39730000031 |
| 74. | Benn, R.; Mynott, R.; Topalovic, I.; Scott, F. Organometallics 1989, 8, 2299. doi:10.1021/om00112a002 |
| 42. |
Clot, E.; Eisenstein, O.; Jasim, N.; Macgregor, S. A.; McGrady, J. E.; Perutz, R. N. Acc. Chem. Res. 2011, 44, 333. doi:10.1021/ar100136x
see for a review. |
| 74. | Benn, R.; Mynott, R.; Topalovic, I.; Scott, F. Organometallics 1989, 8, 2299. doi:10.1021/om00112a002 |
| 22. | Albright, T. A.; Burdett, J.; Whangbo, M.-H. Orbital Interactions in Chemistry, 2nd ed.; Wiley: Hoboken, 2013; pp 537–544; 549–552. doi:10.1002/9781118558409 |
| 46. | Reinhold, M.; McGrady, J. E.; Perutz, R. N. J. Am. Chem. Soc. 2004, 126, 5268. doi:10.1021/ja0396908 |
| 40. | Eisch, J. J.; Piotrowski, A. M.; Aradi, A. A.; Krüger, C.; Romão, M. J. Z. Naturforsch., B 1985, 40, 624. doi:10.1515/znb-1985-0511 |
| 45. | Li, T.; García, J. J.; Brennessel, W. W.; Jones, W. D. Organometallics 2010, 29, 2430. doi:10.1021/om100001m |
| 46. | Reinhold, M.; McGrady, J. E.; Perutz, R. N. J. Am. Chem. Soc. 2004, 126, 5268. doi:10.1021/ja0396908 |
| 49. | Jandl, C.; Öfele, K.; Kühn, F. E.; Herrmann, W. A.; Pöthig, A. Organometallics 2014, 33, 6398. doi:10.1021/om500738d |
| 49. | Jandl, C.; Öfele, K.; Kühn, F. E.; Herrmann, W. A.; Pöthig, A. Organometallics 2014, 33, 6398. doi:10.1021/om500738d |
| 53. | Claus, K. H.; Krüger, C. Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 1988, C44, 1632. doi:10.1107/S0108270188005840 |
| 54. | Laird, B. B.; Davis, R. E. Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 1982, B38, 678. doi:10.1107/S0567740882003781 |
| 55. |
Schager, F.; Haack, K.-J.; Mynott, R.; Rufińska, A.; Pörschke, K.-R. Organometallics 1998, 17, 807. doi:10.1021/om970762b
and references therein. |
| 52. |
Fallon, T.; Willis, A. C.; Rae, A. D.; Paddon-Row, M. N.; Sherburn, M. S. Chem. Sci. 2012, 3, 2133. doi:10.1039/c2sc20130e
and references therein. |
| 2. |
Cotton, F. A. Inorg. Chem. 2002, 41, 643. doi:10.1021/ic010972n
and references therein. |
| 51. | Mackay, E. G.; Newton, C. G.; Toombs-Ruane, H.; Lindeboom, E. J.; Fallon, T.; Willis, A. C.; Paddon-Row, M. N.; Sherburn, M. S. J. Am. Chem. Soc. 2015, 137, 14653. doi:10.1021/jacs.5b07445 |
| 51. | Mackay, E. G.; Newton, C. G.; Toombs-Ruane, H.; Lindeboom, E. J.; Fallon, T.; Willis, A. C.; Paddon-Row, M. N.; Sherburn, M. S. J. Am. Chem. Soc. 2015, 137, 14653. doi:10.1021/jacs.5b07445 |
| 50. | Barkovich, A. J.; Strauss, E. S.; Vollhardt, K. P. C. J. Am. Chem. Soc. 1977, 99, 8321. doi:10.1021/ja00467a036 |
| 51. | Mackay, E. G.; Newton, C. G.; Toombs-Ruane, H.; Lindeboom, E. J.; Fallon, T.; Willis, A. C.; Paddon-Row, M. N.; Sherburn, M. S. J. Am. Chem. Soc. 2015, 137, 14653. doi:10.1021/jacs.5b07445 |
| 57. | Carl, R. T.; Corcoran, E. W., Jr.; Hughes, R. P.; Samkoff, D. E. Organometallics 1990, 9, 838. doi:10.1021/om00117a046 |
| 58. | Hughes, R. P. J. Fluorine Chem. 2010, 131, 1059. doi:10.1016/j.jfluchem.2010.06.014 |
| 59. |
Klärner, F.-G. Angew. Chem., Int. Ed. 2001, 40, 3977. doi:10.1002/1521-3773(20011105)40:21<3977::AID-ANIE3977>3.0.CO;2-N
and references therein. |
| 56. | Bach, I.; Pörschke, K.-R.; Proft, B.; Goddard, R.; Kopiske, C.; Krüger, C.; Rufińska, A.; Seevogel, K. J. Am. Chem. Soc. 1997, 119, 3773. doi:10.1021/ja964210g |
| 1. | Piper, T. S.; Wilkinson, G. J. Inorg. Nucl. Chem. 1956, 3, 104. doi:10.1016/0022-1902(56)80073-0 |
| 10. | Kündig, E. P.; Pape, A. Top. Organomet. Chem. 2004, 7, 71. doi:10.1007/b12823 |
| 25. | Becke, A. D. J. Chem. Phys. 1993, 98, 5648. doi:10.1063/1.464913 |
| 26. | Stephens, P. J.; Devlin, F. J.; Chabalowski, C. F.; Frisch, M. J. J. Phys. Chem. 1994, 98, 11623. doi:10.1021/j100096a001 |
| 27. | Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785. doi:10.1103/PhysRevB.37.785 |
| 62. | Deramchi, K.; Maouche, B.; Kahlal, S.; Saillard, J.-Y. Inorg. Chim. Acta 2011, 370, 499. doi:10.1016/j.ica.2011.02.059 |
| 63. | Li, H.; Feng, H.; Sun, W.; Xie, Y.; King, R. B.; Schaefer, H. F., III. New J. Chem. 2011, 35, 1718. doi:10.1039/c1nj20144a |
| 4. | Gloriozov, I. P.; Marchal, R.; Saillard, J.-Y.; Oprunenko, Y. F. Eur. J. Inorg. Chem. 2015, 250. doi:10.1002/ejic.201402879 |
| 5. | Jiménez-Halla, J. O. C.; Robles, J.; Solá, M. Organometallics 2008, 27, 5230. doi:10.1021/om800505j |
| 6. | Czerwinski, C. J.; Fetisov, E. O.; Gloriozov, I. P.; Oprunenko, Y. F. Dalton Trans. 2013, 42, 10487. doi:10.1039/c3dt50655j |
| 7. | Fetisov, E. O.; Gloriozov, I. P.; Oprunenko, Yu. F.; Saillard, J.-Y.; Kahlal, S. Organometallics 2013, 32, 3512. doi:10.1021/om4003335 |
| 8. | Gridnev, I. D. Coord. Chem. Rev. 2008, 252, 1798. doi:10.1016/j.ccr.2007.10.021 |
| 9. | Oprunenko, Yu. F. Russ. Chem. Rev. 2000, 69, 683. doi:10.1070/RC2000v069n08ABEH000589 |
| 3. | Anh, N. T.; Elian, M.; Hoffmann, R. J. Am. Chem. Soc. 1978, 100, 110. doi:10.1021/ja00469a019 |
| 22. | Albright, T. A.; Burdett, J.; Whangbo, M.-H. Orbital Interactions in Chemistry, 2nd ed.; Wiley: Hoboken, 2013; pp 537–544; 549–552. doi:10.1002/9781118558409 |
| 57. | Carl, R. T.; Corcoran, E. W., Jr.; Hughes, R. P.; Samkoff, D. E. Organometallics 1990, 9, 838. doi:10.1021/om00117a046 |
| 58. | Hughes, R. P. J. Fluorine Chem. 2010, 131, 1059. doi:10.1016/j.jfluchem.2010.06.014 |
| 2. |
Cotton, F. A. Inorg. Chem. 2002, 41, 643. doi:10.1021/ic010972n
and references therein. |
| 23. | Massera, C.; Frenking, G. Organometallics 2003, 22, 2758. doi:10.1021/om0301637 |
| 61. | Summerscales, O. T.; Cloke, F. G. N. Coord. Chem. Rev. 2006, 250, 1122. doi:10.1016/j.ccr.2005.11.020 |
| 20. | Silvestre, J.; Albright, T. A. J. Am. Chem. Soc. 1985, 107, 6829. doi:10.1021/ja00310a015 |
| 21. | Silvestre, J.; Albright, T. A. Nouv. J. Chim. 1985, 9659. |
| 23. | Massera, C.; Frenking, G. Organometallics 2003, 22, 2758. doi:10.1021/om0301637 |
| 56. | Bach, I.; Pörschke, K.-R.; Proft, B.; Goddard, R.; Kopiske, C.; Krüger, C.; Rufińska, A.; Seevogel, K. J. Am. Chem. Soc. 1997, 119, 3773. doi:10.1021/ja964210g |
| 16. | Crabtree, R. H.; Parnell, C. P. Organometallics 1984, 3, 1727. doi:10.1021/om00089a022 |
| 17. | Woolf, A.; Chaplin, A. B.; McGrady, J. E.; Alibadi, M. A. M.; Rees, N.; Draper, S.; Murphy, F.; Weller, A. S. Eur. J. Inorg. Chem. 2011, 1614. doi:10.1002/ejic.201001263 |
| 18. | Woolf, A.; Alibadi, M. A. M.; Chaplin, A. B.; McGrady, J. E.; Weller, A. S. Eur. J. Inorg. Chem. 2011, 1626. doi:10.1002/ejic.201001264 |
| 19. | Oprunenko, Yu. F.; Gloriozov, I. P. Russ. Chem. Bull. 2010, 59, 2061. doi:10.1007/s11172-010-0355-1 |
| 24. |
Voora, V. K.; Jordan, K. D. J. Phys. Chem. A 2014, 118, 7201. doi:10.1021/jp408386f
and references therein. |
| 60. | Sánchez-Sanz, G.; Trujillo, C.; Rozas, I.; Alkorta, I. Phys. Chem. Chem. Phys. 2015, 17, 14961. doi:10.1039/C5CP00876J |
| 14. | Albright, T. A.; Dosa, P. I.; Grossmann, T. N.; Khrustalev, V. N.; Oloba, O. A.; Padilla, R.; Paubelle, R.; Stanger, A.; Timofeeva, T. V.; Vollhardt, K. P. C. Angew. Chem., Int. Ed. 2009, 48, 9853. doi:10.1002/anie.200905088 |
| 15. | Albright, T. A.; Drissi, R.; Gandon, V.; Oldenhof, S.; Oloba-Whenu, O. A.; Padilla, R.; Shen, H.; Vollhardt, K. P. C.; Vreeken, V. Chem. – Eur. J. 2015, 21, 4546. doi:10.1002/chem.201406211 |
| 60. | Sánchez-Sanz, G.; Trujillo, C.; Rozas, I.; Alkorta, I. Phys. Chem. Chem. Phys. 2015, 17, 14961. doi:10.1039/C5CP00876J |
| 11. | Hülsen, M.; Norman, P.; Dolg, M. J. Organomet. Chem. 2011, 696, 3861. doi:10.1016/j.jorganchem.2011.08.039 |
| 12. | Nakai, H.; Isobe, K. Coord. Chem. Rev. 2010, 254, 2652. doi:10.1016/j.ccr.2009.12.025 |
| 13. | Dötz, K. H.; Jahr, H. C. Chem. Rec. 2004, 4, 61. doi:10.1002/tcr.20007 |
| 22. | Albright, T. A.; Burdett, J.; Whangbo, M.-H. Orbital Interactions in Chemistry, 2nd ed.; Wiley: Hoboken, 2013; pp 537–544; 549–552. doi:10.1002/9781118558409 |
| 55. |
Schager, F.; Haack, K.-J.; Mynott, R.; Rufińska, A.; Pörschke, K.-R. Organometallics 1998, 17, 807. doi:10.1021/om970762b
and references therein. |
| 31. | Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys. 2005, 7, 3297. doi:10.1039/b508541a |
| 29. | Roy, L. E.; Hay, J. P.; Martin, R. L. J. Chem. Theory Comput. 2008, 4, 1029. doi:10.1021/ct8000409 |
| 30. | Zhao, Y.; Truhlar, D. G. Theor. Chem. Acc. 2008, 120, 215. doi:10.1007/s00214-007-0310-x |
| 67. | Keasey, A.; Bailey, P. M.; Maitlis, P. M. J. Chem. Soc., Chem. Commun. 1978, 142. doi:10.1039/C39780000142 |
| 45. | Li, T.; García, J. J.; Brennessel, W. W.; Jones, W. D. Organometallics 2010, 29, 2430. doi:10.1021/om100001m |
| 46. | Reinhold, M.; McGrady, J. E.; Perutz, R. N. J. Am. Chem. Soc. 2004, 126, 5268. doi:10.1021/ja0396908 |
| 68. | Stanger, A. Organometallics 1991, 10, 2979. doi:10.1021/om00054a082 |
| 69. | Stanger, A.; Vollhardt, K. P. C. Organometallics 1992, 11, 317. doi:10.1021/om00037a054 |
| 70. | Stanger, A.; Weisman, H. J. Organomet. Chem. 1996, 515, 183. doi:10.1016/0022-328X(95)06104-5 |
| 71. | Braun, Y.; Cronin, L.; Higgitt, C. L.; McGrady, J. E.; Perutz, R. N.; Reinhold, M. New J. Chem. 2001, 25, 19. doi:10.1039/B006368L |
| 72. | Hatnean, J. A.; Beck, R.; Borrelli, J. D.; Johnson, S. A. Organometallics 2010, 29, 6077. doi:10.1021/om1008499 |
| 73. | Schaub, T.; Fischer, P.; Steffen, A.; Braun, T.; Radius, U.; Mix, A. J. Am. Chem. Soc. 2008, 130, 9304. doi:10.1021/ja074640e |
| 74. | Benn, R.; Mynott, R.; Topalovic, I.; Scott, F. Organometallics 1989, 8, 2299. doi:10.1021/om00112a002 |
| 75. | Oprunenko, Yu. F.; Gloriozov, I. P. Russ. Chem. Bull. 2011, 60, 213. doi:10.1007/s11172-011-0036-8 |
| 64. | Nakasuji, K.; Yamaguschi, M.; Murata, I.; Tatsumi, K.; Nakamura, A. Chem. Lett. 1983, 12, 1489. doi:10.1246/cl.1983.1489 |
| 65. | Nakasuji, K.; Yamaguschi, M.; Murata, I.; Tatsumi, K.; Nakamura, A. Organometallics 1984, 3, 1257. doi:10.1021/om00086a018 |
| 66. | Nakasuji, K.; Yamaguschi, M.; Murata, I.; Nakanishi, H. J. Am. Chem. Soc. 1986, 108, 325. doi:10.1021/ja00262a039 |
| 67. | Keasey, A.; Bailey, P. M.; Maitlis, P. M. J. Chem. Soc., Chem. Commun. 1978, 142. doi:10.1039/C39780000142 |
| 66. | Nakasuji, K.; Yamaguschi, M.; Murata, I.; Nakanishi, H. J. Am. Chem. Soc. 1986, 108, 325. doi:10.1021/ja00262a039 |
| 36. | Mealli, C.; Midollini, S.; Moneti, S.; Sacconi, L.; Silvestre, J.; Albright, T. A. J. Am. Chem. Soc. 1982, 104, 95. doi:10.1021/ja00365a020 |
| 21. | Silvestre, J.; Albright, T. A. Nouv. J. Chim. 1985, 9659. |
| 36. | Mealli, C.; Midollini, S.; Moneti, S.; Sacconi, L.; Silvestre, J.; Albright, T. A. J. Am. Chem. Soc. 1982, 104, 95. doi:10.1021/ja00365a020 |
| 35. | CYLview, 1.0b; Legault, C. Y., Université de Sherbrooke, 2009, http://www.cylview.org. |
| 75. | Oprunenko, Yu. F.; Gloriozov, I. P. Russ. Chem. Bull. 2011, 60, 213. doi:10.1007/s11172-011-0036-8 |
| 45. | Li, T.; García, J. J.; Brennessel, W. W.; Jones, W. D. Organometallics 2010, 29, 2430. doi:10.1021/om100001m |
| 33. | Krishnan, R.; Binkley, J. S.; Seeger, R.; Pople, J. A. J. Chem. Phys. 1980, 72, 650. doi:10.1063/1.438955 |
| 74. | Benn, R.; Mynott, R.; Topalovic, I.; Scott, F. Organometallics 1989, 8, 2299. doi:10.1021/om00112a002 |
| 69. | Stanger, A.; Vollhardt, K. P. C. Organometallics 1992, 11, 317. doi:10.1021/om00037a054 |
| 70. | Stanger, A.; Weisman, H. J. Organomet. Chem. 1996, 515, 183. doi:10.1016/0022-328X(95)06104-5 |
| 31. | Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys. 2005, 7, 3297. doi:10.1039/b508541a |
| 20. | Silvestre, J.; Albright, T. A. J. Am. Chem. Soc. 1985, 107, 6829. doi:10.1021/ja00310a015 |
| 32. | Ditchfield, R.; Hehre, W. J.; Pople, J. A. J. Chem. Phys. 1971, 54, 724. doi:10.1063/1.1674902 |
| 76. | Hoffmann, R.; Swaminathan, S.; Odell, B. G.; Gleiter, R. J. Am. Chem. Soc. 1970, 92, 7091. doi:10.1021/ja00727a013 |
© 2016 Oloba-Whenu et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)