Abstract
Purification by flash chromatography strongly impacts the greenness of a process. Unfortunately, due to the lack of the relevant literature data, very often this impact cannot be assessed thus preventing the comparison of the environmental factors affecting the syntheses. We developed a simple mathematical approach to evaluate the minimum mass intensity of flash chromatography from the retention factor values determined by thin-layer chromatography.
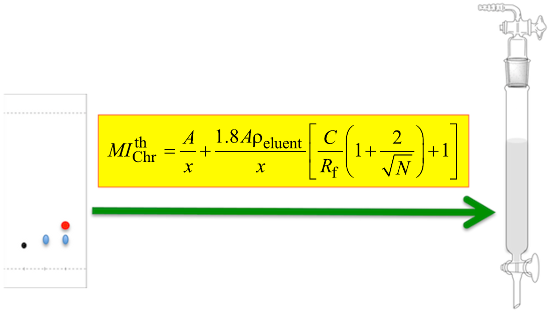
Graphical Abstract
Introduction
As part of a more respectful environmental chemistry, many efforts have been made to reduce the impact of chemical transformations by developing high atom-economic reactions, alternative reaction media or high-performance catalysts. The formation of a pure chemical product not only requires reactants, solvents, promoters and catalysts used in the reaction, but also other materials used for the work-up and for the purification steps. The Sheldon E factor [1,2] and the mass intensity MI [3-5], which are defined according to Equation 1 and Equation 2, respectively, are classical metrics based on the economy of material for evaluating the greenness of a process.
It is worth noting that these mass-based metrics allowed to quantify the mass of waste but did not take into account their potential for negative effects on the environment. These two metrics are related by Equation 3 [6].
The amount of waste includes the amount of the byproducts, but also the amount of non-reacting starting materials, auxiliaries, catalysts or any additives such as acids, bases, salts, solvents of the reaction or solvents required for the work-up and the purification. We demonstrated that the mass intensity could be easily calculated for linear and convergent sequences from the global material economy GME (Equation 4), which is related to the atom economy, the yields of each step, the excess of reactants and the mass of auxiliaries [6,7].
It can be fractioned into three parts: reaction itself (MIR), work-up (MIW) and purification (MIP) as shown by Equation 5 [8].
Any value of the E factor which does not take into account the work-up and purification steps is nonsensical, since the values of MIW and MIP are often much higher than the value of MIR.
In order to compare the greenness of different processes, each term of Equation 5 has to be known. From the literature data it is possible to retrieve information concerning the amount of reactants, solvents and catalysts allowing the calculation of MIR. Moreover, since the work-up is usually well described, it is easy to gain access to MIW. In contrast, the amount of auxiliaries and solvents used in the purification of products is very often omitted. For example, the mass of silica gel and eluents used are never mentioned, which prevents the reader from calculating MIp, and thus having the actual value of the E factor. The impact of chromatography on sustainability was recently discussed [9] and we propose here a method to evaluate such an item. This tool can also allow the chemist to evaluate, from a thin-layer chromatography (TLC), the minimum mass required to perform a flash chromatography. Our calculations are based on the preparative chromatographic technique largely used by chemists [10-12] and on our own experiments.
Results and Discussion
The publication of Still et al. [10] describing flash chromatography in 1978 greatly facilitated the post synthesis purifications which were, until then, often carried out by gravity column chromatography that was time consuming and did not always lead to effective separations. Since then, various automated systems equipped with pumps and eventually detectors and using disposable pre-packed silica cartridges were marketed offering great ease of use.
The mass intensity of purification by chromatography (MIChr) is the ratio between the total mass used to perform the chromatography (i.e., the sum of the mass of silica () and the mass of eluent (meluent)) and mp, the mass of the product (Equation 6).
Mass of silica
The size of the column for chromatography and therefore the amount of silica and solvent depends on the mass of the sample and on the difficulty of separation of the products. This difficulty may be evaluated by ΔRf that is the difference between the retention factor Rf of products in TLC (thin-layer chromatography). Based on their experimentations, Still et al. recommended typical column diameters (constant height) and sample loading for difficult separations (0.2 > ΔRf ≥ 0.1) or more easier separations (ΔRf ≥ 0.2) [10]. Using a column height of 5.9 inches (ca. 15 cm) and considering that the silica has a density of 0.5, correlations have been established between the mass of silica to be used and mass (ms) of the sample to be purified (Table 1, entry 1) [12]. For commercial pre-packed cartridge indications are also provided [13-15] and we have selected some data to obtain a general trend (Table 1).
Table 1: Mass of silica (in grams) to be used depending on the mass of sample to be purified for manually packed columns and some commercial pre-packed cartridges.
| Entry | Cartridge | Particles shape | Average particle size (μm) |
|
||
|---|---|---|---|---|---|---|
| difficult separation |
moderately
difficult separation |
easy separation | ||||
| 1 | Silica gela | irregular | 40–63 | 151.2 ms + 0.5 | 59.8 ms | |
| 2 | RediSepTM | irregular | 35–70 | 1000 ms | 25 ms | 14. ms |
| 3 |
EasyVario
FlashTM |
irregular | 15–40 | 33.3 ms | ||
| 4 | SNAPTM | irregular | 40–50 | 10 ms | 20 ms | 10 ms |
| 5 | SNAP UltraTM | spherical | 25 | 50 ms | 10 ms | 5 ms |
aManually packed glass column.
The mass of silica required to purify ms g of sample may therefore be estimated by Equation 7. Excluding the equation obtained for difficult separations with the RediSepTM cartridge leading to extremely high values of mass of silica (Table 1, entry 2), and partially the equations obtained with spherical silica (SNAP UltraTM, Table 1, entry 5), the values of A range from 10 to 152.
Mass of eluent
The total amount of solvent required for carrying out a chromatography is composed of the part used to pack the column, of that needed to elute the sample, (i.e., the retention volume VR and the half width of the chromatographic peak ω (Figure 1)), and the void volume V0 that corresponds to the mobile phase volume in the packed column.
![[1860-5397-12-228-1]](/bjoc/content/figures/1860-5397-12-228-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: Chromatographic peak of a compound eluted at a retention volume VR with a width ω.
Figure 1: Chromatographic peak of a compound eluted at a retention volume VR with a width ω.
Considering that the solvent used to pack the column is generally recycled, the volume of eluent required can then be expressed by Equation 8.
Under ideal conditions, the retention volume VR can be related to the Rf by Equation 9.
Some deviations of this equation were observed for silica gel column and a correction factor C was proposed [12], so that VR should be calculated using Equation 10. A value of 0.64 was found for manually packed columns, while for commercial cartridges, the value of C was 0.66.
The half width of the chromatographic peak can be estimated by assuming that the peak is described by a Gaussian with a standard deviation σ (Equation 11).
In this equation, the term N represents the efficiency of the chromatographic column, i.e., the system's ability to elute the same compounds at identical rates in order to obtain thin peaks. N is defined as the number of theoretical plates of the column.
Using Equations 8,10 and 11, the mass of eluent can be expressed by:
The void volume V0 is connected to the column volume VC by the porosity of the silica (
= 0.9) and the volume of the column depends on the mass and density (
= 0.5) of the silica according to Equation 13 and Equation 14.
We can then deduce the following equation for the mass of eluent:
Although N depends on various parameters such as the size of the column, the packing particles, the quality of the packing and the flow of the mobile phase, an average value of 35 was proposed for flash chromatography column [16]. Alternatively, in order to take into account broadening of the chromatographic peaks due to the amount of compounds in the sample, it was proposed [12] to evaluate N as a function of the mass fraction of the product in the sample (mP = xms), for difficult separation (Equation 16, B = 51.70) or more easier separation (Equation 16, B = 33.64).
Mass intensity of a chromatography
As already stated above, the mass intensity of purification by chromatography is the ratio between the total mass mT used to perform the chromatography and the mass mP of the product (Equation 6). The total mass is the sum of the silica and eluent masses that can be expressed from Equation 7 and Equation 15.
Considering x, the mass fraction of the product in the sample the theoretical expression of MIChr becomes:
Application
We chose 4 syntheses whose crude reaction products were purified by flash chromatography to illustrate the calculations developed above (Scheme 1).
Scheme 1: Reactions used as examples. (Substrates and products, all the reagents are not shown).
Scheme 1: Reactions used as examples. (Substrates and products, all the reagents are not shown).
In all cases, C was set at 0.64 and was calculated using Ncalc (Equation 16) or N = 35. The value of
was determined according to the experimental data.
Compound 1, obtained by aldol condensation (Scheme 1, reaction a) in 80% yield [8], was chromatographed on a manually packed column using as eluent a 7:3 cyclohexane–acetone mixture (Table 2, entry 1). The mass fraction of product in the crude reaction mixture (79%) was calculated after chromatography taking into account the isolated mass of 1. The values calculated using Equation 18 with N = 35 or Ncalc (Equation 16, B = 33.64 or B = 51.70) deviated only from 6, 7 and 11% of the experimental value, respectively. Another experiment (a(bis), Table 2, entry 2) led to a crude reaction mixture containing 60% by weight of 1 which was purified using a disposable cartridge (PuriFlash SIHP 30 µm, Interchim) and cyclohexane–AcOEt (7:3) as the eluent. Also in this case, the calculated values were very close to the experimental ones (differences of 1, 3 or 6%).
Table 2:
Comparison of the experimental values of the mass intensity of chromatography () with the theoretical estimated values (
) for various reactions (Scheme 1).
| Entry | Reaction | Rf | A | x | A’ | ρeluent | N | B’ |
|
|
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | a | 0.1 | 49 | 0.79 | 62 | 0.78 |
35
37b 57c |
1072
1065 1019 |
901
896 860 |
962 |
| 2 | a(bis)d | 0.15 | 47 | 0.60 | 78 | 0.81 |
35
42b 65c |
946
928 892 |
843
829 800 |
857 |
| 3 | b | 0.13 | 30 | 0.38 | 79 | 0.89 |
35
51b 79c |
1074
1033 995 |
1031
994 961 |
1161 |
| 4 | c | 0.30 | 20 | 0.42 | 47 | 0.65 |
35
49b 76c |
324
314 304 |
258
252 245 |
250 |
| 5 | d | 0.20 | 30 | 0.61 | 49 | 0.81 |
35
42b 64c |
468
459 442 |
427
421 407 |
458 |
aCalculated with the exact values and not with the rounded off numbers A’ and B’. bCalculated using Equation 16 with B = 33.64; cCalculated using Equation 16 with B = 51.70. dReaction a, other experimental conditions.
The crude mixture of reaction b, a bromination in alpha position of a ketone leading to 2 [17,18] in 54% yield, was chromatographed using AcOEt–MeOH (9:1) as the eluent [8]. The mass fraction of compound 2 in the sample was only 38%, leading to high value of (Table 2, entry 3). The calculations lead to
values having differences of 11, 14 and 17% compared to the experimental value. Obviously the lower is the proportion by weight of the compound in the sample, the higher is the mass intensity for the chromatography. This variation in (1/x) was represented for reaction b in Figure 2. Therefore when this proportion is not precisely known, which is the most frequent case before performing the purification, it is possible to estimate a minimum value of MIChr setting x = 1, or, if the mass of the sample to be purified is higher than the theoretical mass of product, x can be calculated assuming a 100% yield (Equation 19).
It is also clear that if a treatment (e.g. extraction) can reduce the mass of the sample to be purified, it would reduce the mass intensity related to chromatography. This should obviously not be to the detriment of the overall mass balance.
![[1860-5397-12-228-2]](/bjoc/content/figures/1860-5397-12-228-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2:
Variation of with x for reaction b (Scheme 1).
Figure 2:
Variation of with x for reaction b (Scheme 1).
This can be illustrated by example c (Scheme 1). In fact, this alkylation reaction was carried out in the presence of a large excess (4 equiv) of dibromobutane to get compound 3 in a good yield (73%) [19]. Some of this excess was removed from the crude reaction product by distillation, reducing the mass of the sample by 53%. This allowed to recycle the reactant but also to greatly reduce the weight of silica to be used (A = 20) and, accordingly the mass of solvent (Table 2, entry 4). This purification with a particularly low MIChr, compared to the other examples, corresponded to a filtration on silica gel rather than to a flash chromatography.
The last example (Scheme 1d) is a S-glycosylation (isolated yield = 62%) leading to compound 4 [20]. For this crude reaction mixture containing 61% of 4, a correct separation was obtained on TLC with the mobile phase cyclohexane–EtOAc (75:25). Again, the values obtained by the calculation were close to the experimental ones, with differentials of 7, 8 and 11% depending on the value taken for N (Table 2, entry 5).
In each case, the calculation afforded values close (deviations <17%) to the experimental value (Figure 3). As already pointed out above, the calculation depends on the value of x that it is not always easy to estimate, but it is possible to estimate a minimum of the mass of intensity related to the chromatography by setting x closed to 1.
![[1860-5397-12-228-3]](/bjoc/content/figures/1860-5397-12-228-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: Comparison between calculated and experimental values of MIChr for the reactions of Scheme 1.
Figure 3: Comparison between calculated and experimental values of MIChr for the reactions of Scheme 1.
The value of MIChr also depends on the retention factor (Rf), especially when the latter is less than 0.2 (Figure 4). An estimation of the minimum is also possible by setting an Rf to a value close to 0.35, as recommended in the seminal paper of Still et al. [10].
![[1860-5397-12-228-4]](/bjoc/content/figures/1860-5397-12-228-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4:
Variation of (N = 35) with Rf for the reactions of Scheme 1.
Figure 4:
Variation of (N = 35) with Rf for the reactions of Scheme 1.
Conclusion
If the impact of chromatography on the environmental factor E of a process seems pretty obvious, we have developed here a tool to quantify it. In an extremely favourable case with a 95% pure sample (x = 0.95), a very easy separation achievable with a small mass of silica (A = 10) and Rf = 0.35, we find, for low density eluent (0.6), an MIChr value close to 50. By doubling the amount of silica, which is closer to reality, the MIChr value is about 100. In real cases chosen here as examples, we have shown that the values were fairly between about 200 and 1200.
Since it is clear that chromatography should be avoided wherever possible, works proposing alternative purification methods have been published [9,21,22]. When the purification by flash chromatography is necessary, solvents with low environmental impacts should be used [23-25]. In this context, super critical chromatography which allows to obtain very low retention volumes and easy recycling offers an interesting alternative [26] but requires a significant investment.
References
-
Sheldon, R. A. CHEMTECH 1994, 24, 38–47.
Return to citation in text: [1] -
Sheldon, R. A. Green Chem. 2007, 9, 1273–1283. doi:10.1039/b713736m
Return to citation in text: [1] -
Curzons, A. D.; Constable, D. J. C.; Mortimer, D. N.; Cunningham, V. L. Green Chem. 2001, 3, 1–6. doi:10.1039/b007871i
Return to citation in text: [1] -
Constable, D. J. C.; Curzons, A. D.; Cunningham, V. L. Green Chem. 2002, 4, 521–527. doi:10.1039/B206169B
Return to citation in text: [1] -
Eissen, M.; Metzger, J. O. Chem. – Eur. J. 2002, 8, 3580–3585. doi:10.1002/1521-3765(20020816)8:16<3580::AID-CHEM3580>3.0.CO;2-J
Return to citation in text: [1] -
Augé, J. Green Chem. 2008, 10, 225–231. doi:10.1039/B711274B
Return to citation in text: [1] [2] -
Augé, J.; Scherrmann, M.-C. New J. Chem. 2012, 36, 1091–1098. doi:10.1039/c2nj20998e
Return to citation in text: [1] -
Pessel, F.; Billault, I.; Scherrmann, M.-C. Green Chem. 2016, 18, 5558–5568. doi:10.1039/C6GC01647B
Return to citation in text: [1] [2] [3] -
Peterson, E. A.; Dillon, B.; Raheem, I.; Richardson, P.; Richter, D.; Schmidt, R.; Sneddon, H. F. Green Chem. 2014, 16, 4060–4075. doi:10.1039/C4GC00615A
Return to citation in text: [1] [2] -
Still, W. C.; Kahn, M.; Mitra, A. J. Org. Chem. 1978, 43, 2923–2925. doi:10.1021/jo00408a041
Return to citation in text: [1] [2] [3] [4] -
Stevens, W. C., Jr.; Hill, D. C. Mol. Diversity 2009, 13, 247–252. doi:10.1007/s11030-008-9104-x
Return to citation in text: [1] -
Fair, J. D.; Kormos, C. M. J. Chromatogr. A 2008, 1211, 49–54. doi:10.1016/j.chroma.2008.09.085
Return to citation in text: [1] [2] [3] [4] -
Effective Organic Compound Purification - Guideline and tactics for Flash Chromatography, 4th ed.; Teledyne Isco Inc, 2010.
(www.isco.com).
Return to citation in text: [1] -
New Generation of Ready to Connect Cartridges using MERCK silica. EasyVarioFlash® (Götec-Labortechnik GmbH), 2007; http://www.swisslabs.eu/uploads/files/Flash_Chromatography_New_Generation_ReadytoUse_Cartridges.pdf.
Return to citation in text: [1] -
Biotage Flash Cartridge User Guide - The Definitive Guide to Flash Chromatography. Biotage, 2014; http://www.biotage.com/product-group/flash-cartridges.
Return to citation in text: [1] -
Meyer, V. R. Practical high-performance liquid chromatography; Wiley, 2010. doi:10.1002/9780470688427
Return to citation in text: [1] -
Howard, S.; Withers, S. G. J. Am. Chem. Soc. 1998, 120, 10326–10331. doi:10.1021/ja981580r
Return to citation in text: [1] -
Billault, I.; Pessel, F.; Petit, A.; Turgis, R.; Scherrmann, M.-C. New J. Chem. 2015, 39, 1986–1995. doi:10.1039/C4NJ01784F
Return to citation in text: [1] -
Turgis, R.; Billault, I.; Acherar, S.; Augé, J.; Scherrmann, M.-C. Green Chem. 2013, 15, 1016–1029. doi:10.1039/c3gc37097f
Return to citation in text: [1] -
Ferrier, R. J.; Furneaux, R. H. Carbohydr. Res. 1976, 52, 63–68. doi:10.1016/S0008-6215(00)85946-7
Return to citation in text: [1] -
Prosa, N.; Turgis, R.; Piccardi, R.; Scherrmann, M.-C. Eur. J. Org. Chem. 2012, 2188–2200. doi:10.1002/ejoc.201101726
Return to citation in text: [1] -
Weiß, M.; Brinkmann, T.; Gröger, H. Green Chem. 2010, 12, 1580–1588. doi:10.1039/c002721a
Return to citation in text: [1] -
MacMillan, D. S.; Murray, J.; Sneddon, H. F.; Jamieson, C.; Watson, A. J. B. Green Chem. 2012, 14, 3016–3019. doi:10.1039/c2gc36378j
Return to citation in text: [1] -
Taygerly, J. P.; Miller, L. M.; Yee, A.; Peterson, E. A. Green Chem. 2012, 14, 3020–3025. doi:10.1039/c2gc36064k
Return to citation in text: [1] -
Pena-Pereira, F.; Kloskowski, A.; Namiesnik, J. Green Chem. 2015, 17, 3667–3705. doi:10.1039/C5GC00611B
Return to citation in text: [1] -
Miller, L.; Mahoney, M. J. Chromatogr. A 2012, 1250, 264–273. doi:10.1016/j.chroma.2012.06.029
Return to citation in text: [1]
| 20. | Ferrier, R. J.; Furneaux, R. H. Carbohydr. Res. 1976, 52, 63–68. doi:10.1016/S0008-6215(00)85946-7 |
| 8. | Pessel, F.; Billault, I.; Scherrmann, M.-C. Green Chem. 2016, 18, 5558–5568. doi:10.1039/C6GC01647B |
| 19. | Turgis, R.; Billault, I.; Acherar, S.; Augé, J.; Scherrmann, M.-C. Green Chem. 2013, 15, 1016–1029. doi:10.1039/c3gc37097f |
| 1. | Sheldon, R. A. CHEMTECH 1994, 24, 38–47. |
| 2. | Sheldon, R. A. Green Chem. 2007, 9, 1273–1283. doi:10.1039/b713736m |
| 8. | Pessel, F.; Billault, I.; Scherrmann, M.-C. Green Chem. 2016, 18, 5558–5568. doi:10.1039/C6GC01647B |
| 8. | Pessel, F.; Billault, I.; Scherrmann, M.-C. Green Chem. 2016, 18, 5558–5568. doi:10.1039/C6GC01647B |
| 6. | Augé, J. Green Chem. 2008, 10, 225–231. doi:10.1039/B711274B |
| 7. | Augé, J.; Scherrmann, M.-C. New J. Chem. 2012, 36, 1091–1098. doi:10.1039/c2nj20998e |
| 17. | Howard, S.; Withers, S. G. J. Am. Chem. Soc. 1998, 120, 10326–10331. doi:10.1021/ja981580r |
| 18. | Billault, I.; Pessel, F.; Petit, A.; Turgis, R.; Scherrmann, M.-C. New J. Chem. 2015, 39, 1986–1995. doi:10.1039/C4NJ01784F |
| 16. | Meyer, V. R. Practical high-performance liquid chromatography; Wiley, 2010. doi:10.1002/9780470688427 |
| 3. | Curzons, A. D.; Constable, D. J. C.; Mortimer, D. N.; Cunningham, V. L. Green Chem. 2001, 3, 1–6. doi:10.1039/b007871i |
| 4. | Constable, D. J. C.; Curzons, A. D.; Cunningham, V. L. Green Chem. 2002, 4, 521–527. doi:10.1039/B206169B |
| 5. | Eissen, M.; Metzger, J. O. Chem. – Eur. J. 2002, 8, 3580–3585. doi:10.1002/1521-3765(20020816)8:16<3580::AID-CHEM3580>3.0.CO;2-J |
| 12. | Fair, J. D.; Kormos, C. M. J. Chromatogr. A 2008, 1211, 49–54. doi:10.1016/j.chroma.2008.09.085 |
| 10. | Still, W. C.; Kahn, M.; Mitra, A. J. Org. Chem. 1978, 43, 2923–2925. doi:10.1021/jo00408a041 |
| 13. |
Effective Organic Compound Purification - Guideline and tactics for Flash Chromatography, 4th ed.; Teledyne Isco Inc, 2010.
(www.isco.com). |
| 14. | New Generation of Ready to Connect Cartridges using MERCK silica. EasyVarioFlash® (Götec-Labortechnik GmbH), 2007; http://www.swisslabs.eu/uploads/files/Flash_Chromatography_New_Generation_ReadytoUse_Cartridges.pdf. |
| 15. | Biotage Flash Cartridge User Guide - The Definitive Guide to Flash Chromatography. Biotage, 2014; http://www.biotage.com/product-group/flash-cartridges. |
| 23. | MacMillan, D. S.; Murray, J.; Sneddon, H. F.; Jamieson, C.; Watson, A. J. B. Green Chem. 2012, 14, 3016–3019. doi:10.1039/c2gc36378j |
| 24. | Taygerly, J. P.; Miller, L. M.; Yee, A.; Peterson, E. A. Green Chem. 2012, 14, 3020–3025. doi:10.1039/c2gc36064k |
| 25. | Pena-Pereira, F.; Kloskowski, A.; Namiesnik, J. Green Chem. 2015, 17, 3667–3705. doi:10.1039/C5GC00611B |
| 10. | Still, W. C.; Kahn, M.; Mitra, A. J. Org. Chem. 1978, 43, 2923–2925. doi:10.1021/jo00408a041 |
| 12. | Fair, J. D.; Kormos, C. M. J. Chromatogr. A 2008, 1211, 49–54. doi:10.1016/j.chroma.2008.09.085 |
| 26. | Miller, L.; Mahoney, M. J. Chromatogr. A 2012, 1250, 264–273. doi:10.1016/j.chroma.2012.06.029 |
| 10. | Still, W. C.; Kahn, M.; Mitra, A. J. Org. Chem. 1978, 43, 2923–2925. doi:10.1021/jo00408a041 |
| 11. | Stevens, W. C., Jr.; Hill, D. C. Mol. Diversity 2009, 13, 247–252. doi:10.1007/s11030-008-9104-x |
| 12. | Fair, J. D.; Kormos, C. M. J. Chromatogr. A 2008, 1211, 49–54. doi:10.1016/j.chroma.2008.09.085 |
| 10. | Still, W. C.; Kahn, M.; Mitra, A. J. Org. Chem. 1978, 43, 2923–2925. doi:10.1021/jo00408a041 |
| 9. | Peterson, E. A.; Dillon, B.; Raheem, I.; Richardson, P.; Richter, D.; Schmidt, R.; Sneddon, H. F. Green Chem. 2014, 16, 4060–4075. doi:10.1039/C4GC00615A |
| 12. | Fair, J. D.; Kormos, C. M. J. Chromatogr. A 2008, 1211, 49–54. doi:10.1016/j.chroma.2008.09.085 |
| 9. | Peterson, E. A.; Dillon, B.; Raheem, I.; Richardson, P.; Richter, D.; Schmidt, R.; Sneddon, H. F. Green Chem. 2014, 16, 4060–4075. doi:10.1039/C4GC00615A |
| 21. | Prosa, N.; Turgis, R.; Piccardi, R.; Scherrmann, M.-C. Eur. J. Org. Chem. 2012, 2188–2200. doi:10.1002/ejoc.201101726 |
| 22. | Weiß, M.; Brinkmann, T.; Gröger, H. Green Chem. 2010, 12, 1580–1588. doi:10.1039/c002721a |
© 2016 Pessel et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)