Abstract
The presence of strong stereoelectronic interactions involving the substituents in cis-2-substituted cyclohexanes may lead to results different from those expected. In this work, we studied the conformational behavior of cis-2-fluoro- (F), cis-2-chloro- (Cl), cis-2-bromo- (Br) and cis-2-iodocyclohexylamine (I) by dynamic NMR and theoretical calculations. The experimental data pointed to an equilibrium strongly shifted toward the ea conformer (equatorial amine group and axial halogen), with populations greater than 90% for F, Cl and Br in both dichloromethane-d2 and methanol-d4. Theoretical calculations (M06-2X/6-311++G(2df,2p)) were in agreement with the experimental, with no influence of the solvent or the halogen on the equilibrium. A principal component analysis of natural bond orbital energies pointed to the σ*C–X and σC–H orbitals and the halogen lone pairs (LPX) as the most significant for the hyperconjugative interactions that influenced the equilibrium. The σC–H → σ*C–X hyperconjugation and the interactions involving the LPX counterbalance each other, explaining the non-influence of the halogen on the conformational equilibrium. These interactions are responsible for the strong preference for the ea conformer in cis-2-halocyclohexylamines, being strong enough to restrain the shift in the equilibrium due to other factors such as steric repulsion or solvent effects.

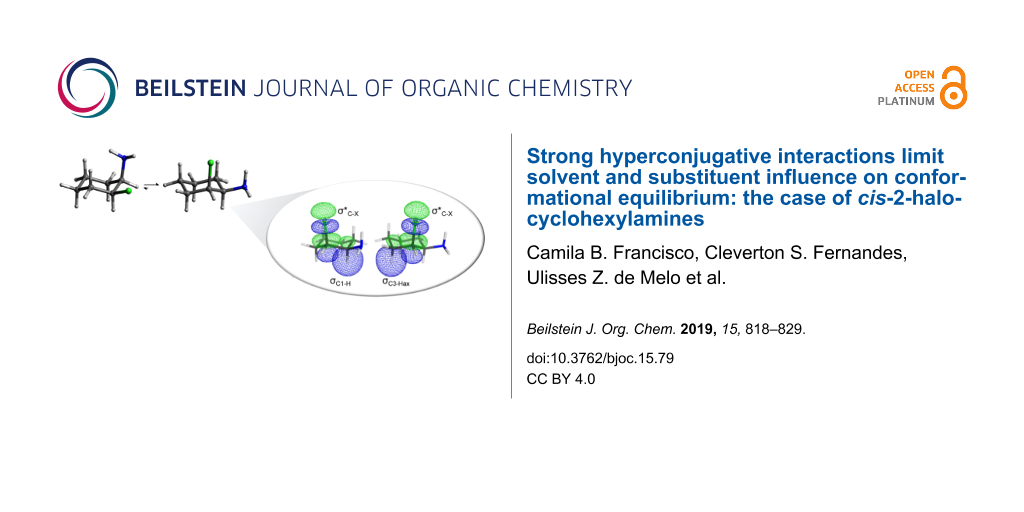
Graphical Abstract
Introduction
cis-2-Substituted cyclohexanes are interesting from the conformational point of view, since one of the substituents should be axial. Generally, bulky substituents prefer the equatorial position to avoid steric repulsions [1]. Nevertheless, two distinct groups may provoke a competition of interactions, with regard to their volumes and steric repulsions, and the particular effects of the solvation medium on them, besides the intrinsic stereoelectronic effects. The sum of these factors in a system may lead to results different from those expected by considering just simple generalizations [2-9].
In the case of cis-2-halocyclohexylamines, the balance of interactions occurs between an amine group, which is known to be sensitive to the solvent [2,10,11], and the halogen, where the size increases considerably from F to I.
Batchelor reported the solvent effects on cis-2-methylcyclohexylamine [11], where the variation from aprotic to protic solvent causes a significant shift in the equilibrium, changing the axial preference of the amine group, which becomes equatorial with the protonation of the nitrogen.
The variation in the halogen size is also expected to cause some effect on the conformational equilibrium. Freitas and co-workers have demonstred this effect on trans-1,2-dihalocyclohexanes [12], where the diequatorial repulsion between the bulky halogens make the diaxial conformer more stable. Similarly, in trans-2-halocyclohexanols the OH–X interaction that stabilizes the diequatorial conformer loses strength for steric repulsions in going from F to I [13]. However, in the behavior observed by Basso and co-workers for cis-2-halocyclohexanols [14], the axial preference of the halogen (about 60–70%) is not greatly affected by the increase in the halogen size. Instead, the equilibrium is influenced by solute–solvent hydrogen bonding with the hydroxy group.
Besides the classical effects, interactions such as hyperconjugation has been pointed out as relevant in several studies involving cyclohexane derivatives [4,12,15-20]. Since the positions of both bonding and antibonding orbitals of the substituents change with the ring inversion, a conformation where a given substituent favors these interactions by performing them more effectively, may, in fact, govern the equilibrium. The C–X bonds have already been reported as excellent electron-density acceptors, and their presence in a system suggests the possibility of these interactions [17,21].
Although there have been several works on the conformational preference of 1,2-disubstituted cyclohexanes [4,11-14,20,22-29], cis-2-halocyclohexylamines have not yet been consistently studied. This is quite surprising, due to the possibilities of effects that add up or compete with each other in the presence of these two groups. This gap in the literature may be attributed to experimental difficulties in obtaining these derivatives.
Therefore, in this work, we developed the study of cis-2-fluorocyclohexylamine (F), cis-2-chlorocyclohexylamine (Cl), cis-2-bromocyclohexylamine (Br) and cis-2-iodocyclohexylamine (I), the latter being only theoretical (due to experimental difficulties). We evaluated the conformational equilibrium between ae (axial amine group and equatorial halogen) and ea (equatorial amine group and axial halogen) conformers (Figure 1) by dynamic NMR (DNMR) and theoretical calculations.
Figure 1: Conformations of cis-2-halocyclohexylamines, where X = F, Cl, Br and I.
Figure 1: Conformations of cis-2-halocyclohexylamines, where X = F, Cl, Br and I.
Results and Discussion
Experimental conformational population
Low-temperature NMR experiments allow the identification of the individual conformers and their population at equilibrium, determined through the integration of 1H and 13C NMR spectra at −80 °C. Figure 2 illustrates the changes in the 1H NMR spectra of cis-2-chlorocyclohexylamine in dichloromethane-d2 by varying the temperature from 25 to −80 °C.
![[1860-5397-15-79-2]](/bjoc/content/figures/1860-5397-15-79-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Variable-temperature 1H NMR spectra (500.13 MHz) for cis-2-chlorocyclohexylamine in dichloromethane-d2.
Figure 2: Variable-temperature 1H NMR spectra (500.13 MHz) for cis-2-chlorocyclohexylamine in dichloromethane-...
At 25 ºC, the signal at 2.89 ppm corresponds to H1, vicinal to nitrogen, and the signal at 4.32 ppm to H2, vicinal to chlorine (Figure 2). These 1H resonances, at room temperature, correspond to the average of the conformers at equilibrium. Table 1 shows the spectral data for F, Cl and Br at 25 and −80 °C, where 3JH–H refers to the individual coupling constants with the vicinal hydrogens, and W is the sum of all couplings, the latter being useful when there is loss of definition or signal broadening, common in low-temperature experiments [29].
Table 1: Chemical shifts (δ, ppm), coupling constants (3JH–H, Hz) and half-height line width (W, Hz) for cis-2-halocyclohexylamines in different solvents at 25 °C and −80 °C.
| Hydrogen | δa | 3JH-Hb | W | δa | 3JH-Hb | W | δa | 3JH-Hb | W | ||||
| Fluorine | Chlorine | Bromine | |||||||||||
| dichloromethane-d2 | 25 °C | H1 | 2.73 | 10.21c | 19.21 | 2.89 | 8.96 | 19.42 | 2.97 | 9.81 | 17.83 | ||
| H2 | 4.60 | 4.74c | 11.36 | 4.32 | 5.72 | 12.99 | 4.68 | 5.65 | 11.10 | ||||
| −80 °C | H1ax | 2.62 | 11.86c | 22.76 | 2.81 | 11.48 | 20.61 | 3.03 | d | d | |||
| H1eq | 3.37 | d | 16.89 | 3.25 | 3.33 | 10.54 | 3.52 | d | d | ||||
| H2ax | 4.55 | d | 23.18 | 4.17 | 10.69 | 22.46 | 4.80 | d | d | ||||
| H2eq | 4.72 | d | 10.16 | 4.46 | d | 10.15 | 4.88 | d | d | ||||
| methanol-d4 | 25 °C | H1 | 2.70 | 10.83c | 19.32 | 2.86 | 9.48 | 19.45 | 2.90 | d | 18.53 | ||
| H2 | 4.64 | 4.40c | 10.59 | 4.37 | 5.40 | 12.18 | 4.64 | 3.61 | 10.51 | ||||
| −80 °C | H1ax | 2.58 | 12.01c | 20.59 | 2.78 | 11.51 | 20.73 | 2.97 | d | d | |||
| H1eq | 3.21 | d | 12.52 | 3.10 | 3.31 | 11.32 | 3.32 | d | d | ||||
| H2ax | 4.48 | d | 23.11 | 4.19 | 12.16 | 22.47 | 4.76 | d | d | ||||
| H2eq | 4.65 | 2.56c | 8.10 | 4.41 | d | 8.10 | 4.67 | d | d | ||||
aIn relation to TMS as reference. bLargest H–H coupling constant at three bonds. cMeasured considering only the 3JH–H coupling, disregarding 2JH–F. dJ and W were not measured due to loss of resolution or signals broadening at −80 °C.
According to the coupling constants (3JH–H) and half-height line widths (W) measured at 25 °C, the dominant conformation is ea. The higher values of J and W for H1 indicate the diaxial coupling of this hydrogen with the axial hydrogen of C6 (Figure 1). This behavior was observed for all compounds, in both solvents, as shown in Table 1.
At −80 °C, two signals for H1 and H2 are observed, which correspond to ae (H1ax and H2eq) and ea (H1eq and H2ax) conformers individually (Table 1). The values of 3JH–H, δ and W at −80 °C allow the assignment of the signals to the respective conformers, and by the integrals, determination the percentage of each in the equilibrium.
In the case of the bromine derivative, due to the broadening of both 1H and 13C signals and the loss of signal resolution at low temperature, the assignments at −80 °C were made by considering the attributions at 25 °C. So, we assume the ea conformer to be the major, attributing the most intense signals set at −80 °C to this conformer.
The populations determined by the integration of both 1H and 13C NMR spectra at −80 °C and the relative conformational energies are shown in Table 2. The equilibrium is shifted strongly toward the ea conformer, with 90% population for F and Cl and 91% for Br in dichloromethane-d2, while in methanol-d4 the populations were 95, 94 and 91% for F, Cl and Br, respectively. These results clearly show that the equilibrium is non-sensitive to halogen size and solvent effects.
Table 2: Conformational populations and relative conformational energies of cis-2-halocyclohexylamines at −80 °C in different solvents.
| 1H | 13C | Average | ||||||
| % ea | ΔGºa | % ea | ΔGºa | % ea | ΔGºa | |||
| F | ||||||||
| dichloromethane-d2 | 90 | −0.84 | 90 | −0.84 | 90 | −0.84 | ||
| methanol-d4 | 95 | −1.13 | 96 | −1.22 | 95 | −1.13 | ||
| Cl | ||||||||
| dichloromethane-d2 | 90 | −0.84 | 90 | −0.84 | 90 | −0.84 | ||
| methanol-d4 | 93 | −0.99 | 95 | −1.13 | 94 | −1.06 | ||
| Br | ||||||||
| dichloromethane-d2 | 91 | −0.89 | b | – | – | – | ||
| methanol-d4 | 91 | −0.89 | b | – | – | – | ||
aΔG = − RT ln K, where K = nea/nae being nea the population of ea conformer and nae the population of ae conformer. A negative value means that ea is more stable. b 13C integration was not possible due to signal broadening.
A similar axial preference of cyclohexane halo derivatives was observed by Basso and co-workers in cis-2-halocyclohexanols [14], and by de Oliveira and Rittner in trans-3-halocyclohexanols [30]. However, in both studies this preference was not so pronounced as that observed in this work, with a small difference between the populations of the two conformers at equilibrium.
The equatorial preference for the amine group was somehow expected, due to classical steric effects (syn-1,3-diaxial repulsion). On the other hand, the amine group is usually very sensitive to the solvent effect. In addition, the increase in the halogen size could lead to a shift toward the ae conformer (equatorial halogen). In the studied system, no change was observed, and this behavior suggests that other effects can be acting. So, theoretical calculations were performed in order to understand which mechanisms control the conformational preference of these compounds.
Theoretical study
Conformer energy
The potential energy surface (PES) for the dihedral C2–C1–N–H (M06-2X/aug-cc-pVDZ) shows that each conformer has three lower-energy rotamers, identified according to the orientation of the nitrogen lone pair as anti (a) and gauche (gX and gH) to H1 (Figure 3).
![[1860-5397-15-79-3]](/bjoc/content/figures/1860-5397-15-79-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: Potential energy surfaces (PESs) for cis-2-halocyclohexylamines for the C2–C1–N–H dihedral angle rotation at M06-2X/aug-cc-pVDZ in ae (top) and ea (bottom) conformers.
Figure 3: Potential energy surfaces (PESs) for cis-2-halocyclohexylamines for the C2–C1–N–H dihedral angle ro...
Optimization and frequency calculations were performed for these rotamers at different theory levels. A table showing the energies of each rotamer is available in Supporting Information File 1 (Table B1).
We compiled in Table 3 the energy differences between ea and ae conformers (ΔEea), at four different theory levels, together with the theoretical ea populations. The ΔEea values were calculated by the weighted averages of both conformers, considering the rotational populations in each. The negative values, both in gas phase and in solution, indicate that ea is the more stable conformation.
Table 3: Variation of conformational energy (ΔEea, kcal mol−1) and populations of ea conformer determined theoretically in cis-2-halocyclohexylamines.
| Gas phase | Dichloromethane | Methanol | |||||||
| ΔEea | % ea | ΔEea | % ea | ΔEea | % ea | ||||
| M06-2X/aug-cc-pVDZ | F | −0.32 | 74 | −0.69 | 88 | −0.66 | 86 | ||
| Cl | −0.46 | 79 | −0.66 | 86 | −0.70 | 88 | |||
| Br | −0.49 | 81 | −0.89 | 92 | −0.88 | 92 | |||
| I | −0.48 | 81 | −1.02 | 94 | −1.06 | 94 | |||
| RMSDa | 0.131 | 0.270 | |||||||
| M06-2X/6-311++G(2df,2p) | F | −0.36 | 76 | −0.67 | 86 | −0.69 | 87 | ||
| Cl | −0.49 | 80 | −0.76 | 89 | −0.77 | 90 | |||
| Br | −0.50 | 81 | −0.93 | 92 | −0.93 | 92 | |||
| I | −0.36 | 76 | −0.95 | 92 | −0.98 | 93 | |||
| RMSDa | 0.004 | 0.230 | |||||||
| MP2/aug-cc-pVDZ | F | −0.22 | 71 | −0.61 | 78 | −0.73 | 88 | ||
| Cl | −0.22 | 70 | −0.64 | 85 | −0.68 | 87 | |||
| Br | −0.40 | 79 | −0.74 | 81 | −0.87 | 92 | |||
| I | −0.86 | 92 | −1.47 | 98 | −1.50 | 98 | |||
| RMSDa | 0.010 | 0.234 | |||||||
| MP2/6-311++G(2df,2p) | F | −0.16 | 68 | −0.68 | 86 | −0.68 | 87 | ||
| Cl | −0.22 | 70 | −0.68 | 86 | −0.72 | 88 | |||
| Br | −0.17 | 67 | −0.64 | 85 | −0.62 | 85 | |||
| I | −0.16 | 66 | −0.63 | 85 | −0.63 | 86 | |||
| RMSDa | 0.013 | 0.264 | |||||||
aRoot mean square deviation of experimental and theoretical ΔGº, being the last available in Supporting Information File 1 (Table B2).
A trend in energy values was observed at all the theory levels employed in this study, there being a small decrease of ΔEea from gas phase to solution. However, when we compare the ΔEea values for dichloromethane and methanol, the energy variation is too small (Table 3). Likewise, the nature of the halogen also showed a minimal variation in ΔEea values over the series, both in gas phase and in solution. These energetical reports are in agreement with the experimental.
The calculations performed in M06-2X/6-311++G(2df,2p) showed results closer to the experimental, with the lower root mean square deviation (RMSD) error values of 0.004 in dichloromethane and 0.230 in methanol. This shows the efficiency of this theory level to describe the studied systems. The agreement of the energy values in gas phase with those in solution confers reliability to calculations such as natural bond orbitals (NBOs), which are made in the gas phase.
With regard to rotamers, gX in ae conformer and a in ea are the least stable, with smaller populations (calculated in M06-2X/6-311++G(2df,2p)), as shown in Figure 4. This was observed for the calculations performed in the gas phase, and in dichloromethane and methanol.
![[1860-5397-15-79-4]](/bjoc/content/figures/1860-5397-15-79-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: Populations of rotamers a, gX e gH in ae (top) and ea (bottom) conformers of cis-2-halocyclohexylamines in the gas phase, dichloromethane and methanol.
Figure 4: Populations of rotamers a, gX e gH in ae (top) and ea (bottom) conformers of cis-2-halocyclohexylam...
Even though previous works involving cyclohexane halo derivatives reported the axial preference of halogens, as mentioned before, the pronounced ea preference observed in our case led us to investigate the specific effects that may be responsible for this behavior.
Delocalization, electrostatic and steric interactions
In order to determine which effects are responsible for the stabilization of each conformer, we carried out studies of hyperconjugative, steric and electrostatic effects.
The deletion of all non-Lewis natural bond orbitals (M06-2X/6-311++G,2df,2p) disregard all hyperconjugative effects, allowing us to evaluate the conformational preference in the absence of these interactions. Therefore, the total energy of each conformer (Etotal) can be expressed as the sum of Eloc, the localized energy after the deletion of the hyperconjugation, and Edeloc, the delocalization energy [31].
These calculations also provide the total steric exchange energy (Esteric), which describes the electron cloud repulsion [32]. Another parameter evaluated was the total electrostatic energy, Eelect, according molecular mechanics calculations employing the Amber force field GAFF [33].
So, after the deletion of hyperconjugative interactions, we should analyze the delocalization energy, where higher values indicate stronger effects. In Table 4 only the most stable rotamers for each conformation were analyzed. The values of ΔEdeloc show an inversion of the conformational preference for all compounds in the absence of hyperconjugative interactions, and ae becoming the most stable conformer. It is worth noting the increase in the difference of the delocalization energy along the series, suggesting the influence of the halogen in this effect.
Table 4: Variation in total (ΔEtotal), localized (ΔEloc) and delocalization (ΔEdeloc) energies; and absolute total steric exchange (Esteric) and total electrostatic (Eelect) energies, in kcal mol−1, for cis-2-halocyclohexylamines.
| ΔEtotala | ΔEloca | ΔEdeloca | Esterica | Eelectb | |
|---|---|---|---|---|---|
| Fluorine | |||||
| ae | 0.25 | 0.00 | 3.46 | 507.05 | −0.50 |
| ea | 0.00 | 3.21 | 0.00 | 509.24 | −0.22 |
| Chlorine | |||||
| ae | 0.25 | 0.00 | 5.77 | 527.16 | −0.13 |
| ea | 0.00 | 5.52 | 0.00 | 532.02 | 0.18 |
| Bromine | |||||
| ae | 0.32 | 0.00 | 7.56 | 534.05 | −0.09 |
| ea | 0.00 | 7.24 | 0.00 | 535.73 | 0.25 |
| Iodine | |||||
| ae | 0.40 | 0.00 | 8.18 | 514.35 | −0.04 |
| ea | 0.00 | 7.78 | 0.00 | 518.27 | 0.31 |
aM06-2X/6-311++G(2df,2p) in the gas phase. bCalculated using the Amber force field GAFF. Positive values indicate more repulsive interactions.
Taking into account the localized energy (ΔEloc), the ea conformer presented the highest values, and it is consistent with the values of Esteric and Eelect. It shows that, although ea is the most stable conformation, it has the greater steric and electrostatic repulsions.
Analyzing all these effects together, we could observe that hyperconjugation is an important factor to describe the conformational preference. Despite the evident influence of the halogen on hyperconjugation, the balance of these energies reflects in the unchanged equilibrium along the series.
With respect to the rotamers, neither hyperconjugation nor total steric exchange energies can explain the rotational behavior, which is attributed to electrostatic effects only. In the most unstable rotamers of each conformer (gX for ae and a for ea) the nitrogen electron lone pair is oriented toward the halogen, as illustrated in Figure 5, resulting in greater electrostatic repulsions. The values of localized, delocalized, steric and electrostatic energies for all rotamers are available in Supporting Information File 1 (Table B3).
![[1860-5397-15-79-5]](/bjoc/content/figures/1860-5397-15-79-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: Nitrogen lone pair in rotamers gX (ae) and a (ea) oriented towards the halogen, making these rotamers less stable in their respective conformation.
Figure 5: Nitrogen lone pair in rotamers gX (ae) and a (ea) oriented towards the halogen, making these rotame...
Although there is a sum of effects that can govern a conformational equilibrium, for cis-2-halocyclohexylamines the rotational preference is due to electrostatic effects, while the strong and non-sensitive conformational preference for ea can be explained by hyperconjugation. This arouses the interest for a deeper analysis of hyperconjugative interactions.
Principal component analysis (PCA) of natural bond orbitals (NBOs)
In order to interpretate the large number of interactions present in the compound structures, we applied PCA to NBO energies.
For each individual bond, the sum was made of all hyperconjugative stabilization energies (Eij) involving both bonding and antibonding orbitals, as well as the energies of nitrogen and halogen lone-pair interactions (LPN and LPX, respectively), resulting in 22 variables corresponding to all the bonds of the structure of the most stable rotamer in each conformation (see Supporting Information File 2 for full numerical data).
In the PCA (Figure 6), two principal components described 94% of the results. The PC1 is able to differentiate the variables according to the halogens, while the PC2 distinguish the two conformations.
![[1860-5397-15-79-6]](/bjoc/content/figures/1860-5397-15-79-6.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: PCA for 22 variables corresponding to the hyperconjugative interactions for all rotamers in ae and ea conformers of cis-2-halocyclohexylamines. Note that the correlation vectors with the strongest black color has the greater contribution for the PC’s.
Figure 6: PCA for 22 variables corresponding to the hyperconjugative interactions for all rotamers in ae and ...
The fact of the PC1, which has the higher variance in relation to the others, distinguish the halogens following a chemical trend is quite important, since the change in the halogen and consequently in the size of the orbitals directly affects the electronic delocalization.
According to the correlation vectors, the LPX differentiate the variables between the halogens, with the greater weight for the fluoro derivatives. If we analyse the vectors perpendicular to the groups of conformers, it is clear that the variables corresponding to C1–H, C2–X and C3–Hax bonds distinguish the ea conformer from ae.
Then, considering all the interactions existent in both conformations, the ones involving the LPX are important for both conformers. However, what differs them are the interactions with the highest weight for ea.
It is worth mentioning that the variables corresponding to the N–H bonds and LPN has no contribution for the PC’s, confirming that the rotational preference has no influence on the hyperconjugation.
Analyzing the bonds pointed by the PCA as electron density donors (bonding orbitals) or acceptors (antibonding orbitals) in Figure 7, it is clear that the most significant interactions are those involving the C2–X bond acting as electronic density acceptor (σ*C2–X orbital), and the C1–H (σC1–H orbital) and LPX acting as donor.
![[1860-5397-15-79-7]](/bjoc/content/figures/1860-5397-15-79-7.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 7: Sum of bonding (donor) and antibonding (acceptor) orbitals interactions of C1–H, C2–X and C3–Hax bonds and LPX in cis-2-halocyclohexylamines.
Figure 7: Sum of bonding (donor) and antibonding (acceptor) orbitals interactions of C1–H, C2–X and C3–Hax bo...
This shows that hyperconjugative interactions are dependent on the halogen: as the size of the halogen increases, the donor or acceptor ability of the respective orbitals (C–X bonds and antibonds) increases in the same way; however, the LPX follows the reverse order, with a decrease in the donor ability as LPF > LPCl > LPBr > LPI.
These observations allow us to analyze which specific orbitals are responsible for the great stabilization of the ea conformer. Table 5 presents the stabilization energy values (Eij), the difference in energy between the orbitals (Ei − Ej) and the Fock matrix elements (F(i:j)) for the main hyperconjugative interactions.
Table 5: Stabilization energy, Eij (kcal mol−1), orbitals energy difference Ei − Ej (a. u.) and Fock matrix elements F(i;j) (a. u.) of main hyperconjugative interactions in ea conformer of cis-2-halocyclohexylamines.
| Eij | Ei - Ej | F(i;j) | |
|---|---|---|---|
| σC1–H → σ*C2–X | |||
| F | 5.83 | 0.86 | 0.063 |
| Cl | 7.88 | 0.72 | 0.067 |
| Br | 9.13 | 0.66 | 0.069 |
| I | 9.44 | 0.64 | 0.069 |
| σC3–Hax → σ*C2–X | |||
| F | 5.99 | 0.87 | 0.065 |
| Cl | 7.43 | 0.73 | 0.066 |
| Br | 8.39 | 0.67 | 0.067 |
| I | 8.34 | 0.65 | 0.066 |
| LPX → σ*C–Ca | |||
| F | 6.09 | 0.94 | 0.068 |
| Cl | 4.36 | 0.79 | 0.053 |
| Br | 3.40 | 0.76 | 0.046 |
| I | 2.52 | 0.72 | 0.038 |
| LPX → σ*C2–H8 | |||
| F | 6.26 | 0.97 | 0.069 |
| Cl | 4.52 | 0.86 | 0.056 |
| Br | 3.19 | 0.85 | 0.046 |
| I | 2.15 | 0.81 | 0.037 |
aσ*C2–C3 for F, and σ*C1–C2 for Cl, Br and I.
The Eij values for σC1–H → σ*C2–X and σC3–Hax → σ*C2–X clearly show a trend from F to I, where these interactions become considerably more intense (higher Eij values) with the increase in the halogen size. It is also possible to observe that the difference in energy between these orbitals (Ei − Ej) decreases from F to I, which means that the acceptance of electron density by the C–X bond is more effective when we have the larger halogens. The Ei − Ej values decrease from 0.86 for F to 0.64 atomic units for I in σC1–H → σ*C2–X; and from 0.87 for F to 0.65 atomic units for I in σC3–Hax → σ*C2–X. The same trend is observed for the Fock matrix element (F(i:j)), which concerns to the orbital overlap and also increases from F to I .
On the other hand, the interactions involving the LPX follow the reverse order (Table 5). The Eij values decrease steadily from F to I, going from 6.09 and 6.26 to 2.52 and 2.15 kcal mol−1 for LPX → σ*C–C and LPX → σ*C2–H8, respectively. In the same way, the Fock matrix element decreases considerably comparing the LPF and LPI interactions, going from 0.068 and 0.069 for LPF to 0.038 and 0.037 atomic units for LPI, in LPX → σ*C–C and LPX → σ*C2–H8, respectively.
This tendency in the halogen series observed in both hyperconjugative interactions describes the observed in PCA; the LPX interactions counterbalance the σC–H → σ*C2–X, in the sense that the LPX is more important for the fluoro derivatives, while the σC–H → σ*C2–X has the greater weight for the larger halogens.
The acceptor ability of σ*C–X orbitals has already been described in the literature [17], and has an inverse correlation with electronegativity: the electronegativity decreases from F to I and the acceptor ability of σ*C–X orbitals increases in the order σ*C–F < σ*C–Cl < σ*C–Br < σ*C–I, as observed in this work.
As σC1–H, σ*C2–X and σC3–Hax are antiperiplanar, they favor orbital overlap, as illustrated in Figure 8. The orbital σ*C–X acting as electron density acceptor of σC1–H and σC3–Hax can explain the great axial preference of the halogens. While in the ea conformer the donors σC1–H and σC3–Hax are antiperiplanar to the acceptor σ*C–X, in the ae conformer the corresponding donor orbitals are from C–C bonds (due to equatorial halogen orientation). Previous publications have already reported the C–H bond as slightly better donor than C–C bond [34,35].
![[1860-5397-15-79-8]](/bjoc/content/figures/1860-5397-15-79-8.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 8: Orbitals overlap of σC1–H → σ*C2–X (left) and σC3–Hax → σ*C2–X (right) hyperconjugations in ea conformer.
Figure 8: Orbitals overlap of σC1–H → σ*C2–X (left) and σC3–Hax → σ*C2–X (right) hyperconjugations in ea conf...
Therefore, in the sum of interactions existent in the studied systems the hyperconjugation stands out, explaining the axial halogen and equatorial NH2 (ea) preference in all compounds.
Conclusion
The conformational behavior of the cis isomers of 2-fluoro-, 2-chloro- and 2-bromocyclohexylamine was determined experimentally through DNMR at −80 °C, with populations of the ea conformer (equatorial amine group and axial halogen) higher than 90% in dichloromethane-d2 and methanol-d4. The conformational preference was affected neither by the solvent polarity nor the halogen size, suggesting the presence of strong stereoelectronic effects being responsible for the conformational behavior in these systems.
Theoretical calculations are in agreement with experimental data, the ea conformer being the most stable for all series, both in the gas phase and in solution. For the C–N rotation, the most unstable rotamers are gX for the ae conformer and a for ea, due to the orientation of the nitrogen lone pair electrons toward the halogen, which provides greater electrostatic repulsions.
The non-sensitivity to halogen size along the series can be attributed to a balance of steric, electrostatic and hyperconjugative interactions, being the strong conformational preference for ea explained by hyperconjugations involving mainly the C–X bond. The greater acceptor ability of the σ*C–X orbital, axial in the ea conformer, enables strong interactions with the neighboring σC–H orbitals, and this acceptor ability increases along the halogen series (F < Cl < Br < I). However, interactions involving the halogen lone pair electrons follows the reverse order, counterbalancing the σC–H → σ*C–X interactions along the series.
The strongly shifted and non-sensitive conformational equilibrium governed by a strong hyperconjugative interaction in cis-2-halocyclohexylamines shows that the conformational analysis of small molecules can still provide surprising results.
Experimental
Synthesis
trans-2-Fluorocyclohexanol was prepared according the literature [36] to provide cis-2-fluorocyclohexylamine.
cis-2-Fluorocyclohexylamine (F) was obtained by a Mitsunobu–Gabriel reaction, as described by Thvedt and co-workers [37]. Under nitrogen atmosphere, trans-2-fluorocyclohexanol (6.00 mmol), triphenylphosphine (6.60 mmol) and phthalimide (6.60 mmol) were dissolved in THF (40 mL). To this mixture was slowly added a solution of diisopropyl azodicarboxylate (DIAD, 40% in THF) and the mixture was stirred at room temperature for 18 h. The solvent was removed under reduced pressure and the reaction mixture was re-dissolved in CH2Cl2 (20 mL) and 10 mL of a 10% K2CO3 solution and stirred for 1 h. The resulting mixture was washed with distilled water (3 × 10 mL), the organic layer dried with Na2SO4 and concentrated under reduced pressure, and the crude product purified by silica-gel column chromatography (ethyl acetate/hexane 20%), resulting in 1.18 g (80%) of the cis-Gabriel amine. The free amine was obtained by the hydrazinolysis of the cis-Gabriel amine (0.40 mmol), in methanol (0.50 mL) with hydrazine hydrate (25%, 0.20 mL), stirred at room temperature for 24 h. To the mixture was added HCl until pH ≈ 2, forming a precipitate, which was filtered, and to the aqueous phase was added NaOH until pH ≈ 14 and the product extracted exhaustively (6 × 10 mL) with CH2Cl2. The organic layer was dried with Na2SO4 and the pure cis-2-fluorocyclohexylamine (0.19 g, 35%), a yellowish liquid concentrated under reduced pressure.
2-Chloro- and 2-bromocyclohexanone were synthetized as previously described [38,39], to provide cis-2-chloro (Cl) and cis-2-bromocyclohexylamine (Br), respectively, by a reductive amination [40].
To a sealed tube were added the corresponding ketone (10 mmol), ammonium acetate (100 mmol) and sodium cyanoborohydride (10 mmol) in methanol (30 mL) and the mixture stirred for 48 h at room temperature. To the mixture was added concentrated HCl until pH ≈ 2, forming a white precipitate (protonated amine), which was filtered and dissolved in distilled water, which was washed with CH2Cl2 (3 × 20 mL). To the aqueous layer was added NaOH until pH ≈ 14 and the product extracted exhaustively with CH2Cl2 (6 × 20 mL). The crude mixture was purified by silica-gel column chromatography (acetone/chloroform 10% for Cl and 25% for Br), and the cis isomer was isolated corresponding to a yellowish liquid for Cl (0.04 g, 15%) and a white amorphous solid for Br (0.03 g, 10%).
cis-2-Fluorocyclohexylamine: 1H NMR (500.13 MHz, methanol-d4) δ 4.64 (dddd, 1H, H2), 2.70 (dddd, 1H, H1), 2.01 (m, 1H, 1H3), 1.74–1.64 (m, 2H, 1H5, 1H6), 1.61–1.42 (m, 4H, 1H3, 2H4, 1H6), 1.34 (m, 1H, H5); 13C NMR (125.77 MHz, methanol-d4) δ 93.58 (C2), 52.80 (C1), 30.84 (C3, C6), 20.85 (C4), 24.88 (C5); HRMS (ESI/QTOF) m/z: [M + H]+ calcd for C6H12FN, 118.0953; found, 118.0991.
cis-2-Chlorocyclohexylamine: 1H NMR (500.13 MHz, dichloromethane-d2) δ 4.30 (ddd, 1H, H2), 2.80 (ddd, 1H, H1), 2.04 (m, 1H, 1H3), 1.78 (m, 1H, 1H3), 1.70–1.60 (m, 2H, 1H5, 1H4), 1,54 (m, 2H, 2H6), 1.40 (m, 1H, 1H4), 1.30 (m, 1H, 1H5); 13C NMR (125.77 MHz, dichlorotmethane-d2) δ 68.47 (C2), 53.22 (C1), 33.16 (C3), 31.30 (C6), 23.76 (C5), 21.10 (C4); HRMS (ESI/QTOF) m/z: [M + H]+ calcd for C6H12ClN, 134.0658; found, 134.0692.
cis-2-Bromocyclohexylamine: 1H NMR (500.13 MHz, dichloromethane-d2) δ 4.68 (ddd, 1H, H2), 2.97 (ddd, 1H, H1), 2.18 (m, 1H, H3), 1.93 (m, 1H, H3), 1.77–1.63 (m, 4H, 1H4, 1H5, 2H6), 1.50 (m, 1H, H4), 1.37 (m, 1H, H5); 13C NMR (125.77 MHz, dichlorotmethane-d2) δ 62.19 (C1), 53.42 (C2), 33.67 (C3), 30.08 (C5), 23.87 (C6), 21.28 (C4); HRMS (ESI/QTOF) m/z: [M + H]+ calcd for C6H12BrN, 178.0153; found, 178.0189.
NMR experiments
¹H and ¹³C NMR spectra were acquired on a Bruker Avance III HD spectrometer, operating at 500.13 MHz for 1H nuclei and 125.77 MHz for 13C nuclei in solutions with approximate concentration of 0.01 mol L–1 in dichloromethane-d2 and methanol-d4, using tetramethylsilane as internal reference. The probe was coupled to a liquid nitrogen evaporator system to decrease the temperature from 25 to −80 °C. Typical 1H NMR spectra were run with a spectral window of approximately 10000 Hz (20 ppm) for 1H spectra, and 30000 Hz (238 ppm) for 13C spectra, with number of points 32k, resulting in a digital resolution of 0.12 Hz/point. The spectral data are available in Supporting Information File 1.
Theoretical calculations
Theoretical calculations were performed with the software package Gaussian 09 [41]. To determine the lowest energy structures for each conformer, we built a PES (in M06-2X/aug-cc-pVDZ), varying the C2–C1–N–H dihedral angle in steps of 15° manually, to avoid nitrogen inversion.
Optimization and frequency calculations were performed for the three lower-energy rotamers for each conformer, both in the gas phase and in solution (Cartesian coordinates are available in Supporting Information File 1). The calculations were performed using the M06-2X density functional method, and the second-order Möller–Plesset perturbation method (MP2), associated with the Pople 6-311++G(2df,2p), and Dunning aug-cc-pVDZ basis set. The mixed basis set function LanL2DZ-ECP was employed for the iodine atom. Solvation calculations were performed in dichloromethane and methanol, with the the implicit model IEF-PCM and the description of the molecular cavity through Bondi’s atomic radii.
Molecular Mechanics calculations were performed using the software Avogadro 1.2.0 [42], employing the Amber force field GAFF [33].
NBO calculations were performed in the optimized structures in the gas phase (M06-2X/6-311++G(2df,2p)), through the module NBO 5.9 [43] from Gaussian 09. For the PCA, it was used the software R, version 3.5.0 [44], with the graphical interface RStudio, version 1.0.153 [45].
Supporting Information
| Supporting Information File 1: 1H and 13C NMR spectra at 25 and −80 °C, supplementary theoretical values, RScript for PCA and the Cartesian coordinates of the structures. | ||
| Format: PDF | Size: 1.2 MB | Download |
| Supporting Information File 2: NBO data for PCA. | ||
| Format: XLSX | Size: 13.4 KB | Download |
Acknowledgements
The authors would like to thank the Brazilian Council for Scientific and Technological Development (CNPq) for the fellowships to E.A.B. and R.R., and for the scholarship to C.S.F.; and the Coordination for the Improvement of Higher Education Personnel (CAPES) for the scholarships to C.B.F. and U.Z.M. Thanks also go to the São Paulo Research Foundation (FAPESP) (Grant 2016/24109-0) for the financial assistance and to the National Center for High Performance Computing (CENAPAD-UFC) for the computational cluster disponibility.
References
-
Eliel, E. L.; Samuel, H. W. Stereochemistry of Organic Compounds; Wiley-Interscience: New York, 1994.
Return to citation in text: [1] -
de Oliveira, P. R.; Viesser, R. V.; Guerrero, P. G., Jr.; Rittner, R. Spectrochim. Acta, Part A 2011, 78, 1599–1605. doi:10.1016/j.saa.2011.02.010
Return to citation in text: [1] [2] -
de Oliveira, P. R.; Rittner, R. Spectrochim. Acta, Part A 2008, 70, 1079–1086. doi:10.1016/j.saa.2007.10.016
Return to citation in text: [1] -
Duarte, C. J.; Freitas, M. P. J. Mol. Struct. 2009, 930, 135–139. doi:10.1016/j.molstruc.2009.05.004
Return to citation in text: [1] [2] [3] -
Silla, J. M.; Freitas, M. P. Comput. Theor. Chem. 2012, 999, 89–92. doi:10.1016/j.comptc.2012.08.019
Return to citation in text: [1] -
de Oliveira, P. R.; Rittner, R. Spectrochim. Acta, Part A 2005, 61, 1737–1745. doi:10.1016/j.saa.2004.07.004
Return to citation in text: [1] -
Onoda, A.; Haruna, H.; Yamamoto, H.; Takahashi, K.; Kozuki, H.; Okamura, T.-a.; Ueyama, N. Eur. J. Org. Chem. 2005, 641–645. doi:10.1002/ejoc.200400385
Return to citation in text: [1] -
Lambert, K. M.; Stempel, Z. D.; Wiberg, K. B.; Bailey, W. F. Org. Lett. 2017, 19, 6408–6411. doi:10.1021/acs.orglett.7b03287
Return to citation in text: [1] -
Kleinpeter, E.; Werner, P.; Linker, T. Tetrahedron 2017, 73, 3801–3809. doi:10.1016/j.tet.2017.04.029
Return to citation in text: [1] -
Eliel, E. L.; Della, E. W.; Williams, T. H. Tetrahedron Lett. 1963, 4, 831–835. doi:10.1016/s0040-4039(01)90724-5
Return to citation in text: [1] -
Batchelor, J. G. J. Chem. Soc., Perkin Trans. 2 1976, 1585. doi:10.1039/p29760001585
Return to citation in text: [1] [2] [3] -
Freitas, M. P.; Rittner, R.; Tormena, C. F.; Abraham, R. J. Spectrochim. Acta, Part A 2005, 61, 1771–1776. doi:10.1016/j.saa.2004.07.007
Return to citation in text: [1] [2] [3] -
Freitas, M. P.; Tormena, C. F.; Rittner, R. J. Mol. Struct. 2001, 570, 175–180. doi:10.1016/s0022-2860(01)00482-3
Return to citation in text: [1] [2] -
Basso, E. A.; Abiko, L. A.; Gauze, G. F.; Pontes, R. M. J. Org. Chem. 2011, 76, 145–153. doi:10.1021/jo101819u
Return to citation in text: [1] [2] [3] -
Taddei, F.; Kleinpeter, E. J. Mol. Struct.: THEOCHEM 2004, 683, 29–41. doi:10.1016/j.theochem.2004.06.010
Return to citation in text: [1] -
Ribeiro, D. S.; Rittner, R. J. Org. Chem. 2003, 68, 6780–6787. doi:10.1021/jo034421l
Return to citation in text: [1] -
Alabugin, I. V.; Zeidan, T. A. J. Am. Chem. Soc. 2002, 124, 3175–3185. doi:10.1021/ja012633z
Return to citation in text: [1] [2] [3] -
Taddei, F.; Kleinpeter, E. J. Mol. Struct.: THEOCHEM 2005, 718, 141–151. doi:10.1016/j.theochem.2005.01.003
Return to citation in text: [1] -
de Melo, U. Z.; dos Santos Yamazaki, D. A.; de Araújo Cândido, A.; Basso, E. A.; de Freitas Gauze, G. J. Mol. Struct. 2018, 1163, 227–235. doi:10.1016/j.molstruc.2018.01.096
Return to citation in text: [1] -
Lopes Jesus, A. J.; Rosado, M. T. S.; Redinha, J. S. Comput. Theor. Chem. 2011, 964, 32–39. doi:10.1016/j.comptc.2010.11.031
Return to citation in text: [1] [2] -
Alabugin, I. V.; dos Passos Gomes, G.; Abdo, M. A. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2019, 9, e1389. doi:10.1002/wcms.1389
Return to citation in text: [1] -
Bocca, C. C.; Basso, E. A.; Fiorin, B. C.; Tormena, C. F.; dos Santos, F. P. J. Phys. Chem. A 2006, 110, 9438–9442. doi:10.1021/jp061502n
Return to citation in text: [1] -
Basso, E. A.; Kaiser, C.; Rittner, R.; Lambert, J. B. Magn. Reson. Chem. 1994, 32, 205–209. doi:10.1002/mrc.1260320403
Return to citation in text: [1] -
Allinger, N. L.; Pamphilis, N. A. J. Org. Chem. 1973, 38, 316–319. doi:10.1021/jo00942a024
Return to citation in text: [1] -
Yoshida, Z.-i.; Nakagawa, K. Tetrahedron Lett. 1965, 6, 3753–3756. doi:10.1016/s0040-4039(01)99558-9
Return to citation in text: [1] -
Silla, J. M.; Duarte, C. J.; Freitas, M. P.; Ramalho, T. C.; Cormanich, R. A.; Santos, F. P.; Tormena, C. F.; Rittner, R. Spectrochim. Acta, Part A 2011, 81, 359–362. doi:10.1016/j.saa.2011.06.023
Return to citation in text: [1] -
Basso, E. A.; Kaiser, C.; Rittner, R.; Lambert, J. B. J. Org. Chem. 1993, 58, 7865–7869. doi:10.1021/jo00079a035
Return to citation in text: [1] -
Silla, J. M.; Cormanich, R. A.; Duarte, C. J.; Freitas, M. P.; Ramalho, T. C.; Barbosa, T. M.; Santos, F. P.; Tormena, C. F.; Rittner, R. J. Phys. Chem. A 2011, 115, 10122–10127. doi:10.1021/jp206136t
Return to citation in text: [1] -
Cedran, J. C.; dos Santos, F. P.; Basso, E. A.; Tormena, C. F. J. Phys. Chem. A 2007, 111, 11701–11705. doi:10.1021/jp075280k
Return to citation in text: [1] [2] -
de Oliveira, P. R.; Rittner, R. Magn. Reson. Chem. 2008, 46, 250–255. doi:10.1002/mrc.2173
Return to citation in text: [1] -
Reed, A. E.; Weinhold, F. Isr. J. Chem. 1991, 31, 277–285. doi:10.1002/ijch.199100032
Return to citation in text: [1] -
Badenhoop, J. K.; Weinhold, F. J. Chem. Phys. 1997, 107, 5422–5432. doi:10.1063/1.475149
Return to citation in text: [1] -
Wang, J.; Wolf, R. M.; Caldwell, J. W.; Kollman, P. A.; Case, D. A. J. Comput. Chem. 2004, 25, 1157–1174. doi:10.1002/jcc.20035
Return to citation in text: [1] [2] -
Alabugin, I. V. J. Org. Chem. 2000, 65, 3910–3919. doi:10.1021/jo991622+
Return to citation in text: [1] -
Alabugin, I. V.; Manoharan, M. J. Org. Chem. 2004, 69, 9011–9024. doi:10.1021/jo048287w
Return to citation in text: [1] -
Wittig, G.; Mayer, U. Chem. Ber. 1963, 96, 329–341. doi:10.1002/cber.19630960141
Return to citation in text: [1] -
Thvedt, T. H. K.; Fuglseth, E.; Sundby, E.; Hoff, B. H. Tetrahedron 2010, 66, 6733–6743. doi:10.1016/j.tet.2010.06.081
Return to citation in text: [1] -
Lautens, M.; Bouchain, G. Org. Synth. 2002, 79, 251. doi:10.15227/orgsyn.079.0251
Return to citation in text: [1] -
Allinger, J.; Allinger, N. L. Tetrahedron 1958, 2, 64–74. doi:10.1016/0040-4020(58)88024-2
Return to citation in text: [1] -
Borch, R. F.; Bernstein, M. D.; Durst, H. D. J. Am. Chem. Soc. 1971, 93, 2897–2904. doi:10.1021/ja00741a013
Return to citation in text: [1] -
Gaussian 09, Revision B.01; Gaussian, Inc.: Wallingford, CT, 2010.
Return to citation in text: [1] -
Hanwell, M. D.; Curtis, D. E.; Lonie, D. C.; Vandermeersch, T.; Zurek, E.; Hutchison, G. R. J. Cheminf. 2012, 4, 17. doi:10.1186/1758-2946-4-17
Return to citation in text: [1] -
NBO 5.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, 2001.
Return to citation in text: [1] -
R: A Language and Environment for Statistical Computing, Version 3.5.0; R Foundation for Statistical Computing: Vienna, Austria, 2018.
Return to citation in text: [1] -
RStudio: Integrated Development Environment for R, Version 1.0.5.153; RStudio Inc.: Boston, MA, 2016.
Return to citation in text: [1]
| 45. | RStudio: Integrated Development Environment for R, Version 1.0.5.153; RStudio Inc.: Boston, MA, 2016. |
| 1. | Eliel, E. L.; Samuel, H. W. Stereochemistry of Organic Compounds; Wiley-Interscience: New York, 1994. |
| 12. | Freitas, M. P.; Rittner, R.; Tormena, C. F.; Abraham, R. J. Spectrochim. Acta, Part A 2005, 61, 1771–1776. doi:10.1016/j.saa.2004.07.007 |
| 32. | Badenhoop, J. K.; Weinhold, F. J. Chem. Phys. 1997, 107, 5422–5432. doi:10.1063/1.475149 |
| 11. | Batchelor, J. G. J. Chem. Soc., Perkin Trans. 2 1976, 1585. doi:10.1039/p29760001585 |
| 33. | Wang, J.; Wolf, R. M.; Caldwell, J. W.; Kollman, P. A.; Case, D. A. J. Comput. Chem. 2004, 25, 1157–1174. doi:10.1002/jcc.20035 |
| 2. | de Oliveira, P. R.; Viesser, R. V.; Guerrero, P. G., Jr.; Rittner, R. Spectrochim. Acta, Part A 2011, 78, 1599–1605. doi:10.1016/j.saa.2011.02.010 |
| 10. | Eliel, E. L.; Della, E. W.; Williams, T. H. Tetrahedron Lett. 1963, 4, 831–835. doi:10.1016/s0040-4039(01)90724-5 |
| 11. | Batchelor, J. G. J. Chem. Soc., Perkin Trans. 2 1976, 1585. doi:10.1039/p29760001585 |
| 30. | de Oliveira, P. R.; Rittner, R. Magn. Reson. Chem. 2008, 46, 250–255. doi:10.1002/mrc.2173 |
| 2. | de Oliveira, P. R.; Viesser, R. V.; Guerrero, P. G., Jr.; Rittner, R. Spectrochim. Acta, Part A 2011, 78, 1599–1605. doi:10.1016/j.saa.2011.02.010 |
| 3. | de Oliveira, P. R.; Rittner, R. Spectrochim. Acta, Part A 2008, 70, 1079–1086. doi:10.1016/j.saa.2007.10.016 |
| 4. | Duarte, C. J.; Freitas, M. P. J. Mol. Struct. 2009, 930, 135–139. doi:10.1016/j.molstruc.2009.05.004 |
| 5. | Silla, J. M.; Freitas, M. P. Comput. Theor. Chem. 2012, 999, 89–92. doi:10.1016/j.comptc.2012.08.019 |
| 6. | de Oliveira, P. R.; Rittner, R. Spectrochim. Acta, Part A 2005, 61, 1737–1745. doi:10.1016/j.saa.2004.07.004 |
| 7. | Onoda, A.; Haruna, H.; Yamamoto, H.; Takahashi, K.; Kozuki, H.; Okamura, T.-a.; Ueyama, N. Eur. J. Org. Chem. 2005, 641–645. doi:10.1002/ejoc.200400385 |
| 8. | Lambert, K. M.; Stempel, Z. D.; Wiberg, K. B.; Bailey, W. F. Org. Lett. 2017, 19, 6408–6411. doi:10.1021/acs.orglett.7b03287 |
| 9. | Kleinpeter, E.; Werner, P.; Linker, T. Tetrahedron 2017, 73, 3801–3809. doi:10.1016/j.tet.2017.04.029 |
| 31. | Reed, A. E.; Weinhold, F. Isr. J. Chem. 1991, 31, 277–285. doi:10.1002/ijch.199100032 |
| 17. | Alabugin, I. V.; Zeidan, T. A. J. Am. Chem. Soc. 2002, 124, 3175–3185. doi:10.1021/ja012633z |
| 21. | Alabugin, I. V.; dos Passos Gomes, G.; Abdo, M. A. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2019, 9, e1389. doi:10.1002/wcms.1389 |
| 29. | Cedran, J. C.; dos Santos, F. P.; Basso, E. A.; Tormena, C. F. J. Phys. Chem. A 2007, 111, 11701–11705. doi:10.1021/jp075280k |
| 4. | Duarte, C. J.; Freitas, M. P. J. Mol. Struct. 2009, 930, 135–139. doi:10.1016/j.molstruc.2009.05.004 |
| 12. | Freitas, M. P.; Rittner, R.; Tormena, C. F.; Abraham, R. J. Spectrochim. Acta, Part A 2005, 61, 1771–1776. doi:10.1016/j.saa.2004.07.007 |
| 15. | Taddei, F.; Kleinpeter, E. J. Mol. Struct.: THEOCHEM 2004, 683, 29–41. doi:10.1016/j.theochem.2004.06.010 |
| 16. | Ribeiro, D. S.; Rittner, R. J. Org. Chem. 2003, 68, 6780–6787. doi:10.1021/jo034421l |
| 17. | Alabugin, I. V.; Zeidan, T. A. J. Am. Chem. Soc. 2002, 124, 3175–3185. doi:10.1021/ja012633z |
| 18. | Taddei, F.; Kleinpeter, E. J. Mol. Struct.: THEOCHEM 2005, 718, 141–151. doi:10.1016/j.theochem.2005.01.003 |
| 19. | de Melo, U. Z.; dos Santos Yamazaki, D. A.; de Araújo Cândido, A.; Basso, E. A.; de Freitas Gauze, G. J. Mol. Struct. 2018, 1163, 227–235. doi:10.1016/j.molstruc.2018.01.096 |
| 20. | Lopes Jesus, A. J.; Rosado, M. T. S.; Redinha, J. S. Comput. Theor. Chem. 2011, 964, 32–39. doi:10.1016/j.comptc.2010.11.031 |
| 14. | Basso, E. A.; Abiko, L. A.; Gauze, G. F.; Pontes, R. M. J. Org. Chem. 2011, 76, 145–153. doi:10.1021/jo101819u |
| 14. | Basso, E. A.; Abiko, L. A.; Gauze, G. F.; Pontes, R. M. J. Org. Chem. 2011, 76, 145–153. doi:10.1021/jo101819u |
| 13. | Freitas, M. P.; Tormena, C. F.; Rittner, R. J. Mol. Struct. 2001, 570, 175–180. doi:10.1016/s0022-2860(01)00482-3 |
| 4. | Duarte, C. J.; Freitas, M. P. J. Mol. Struct. 2009, 930, 135–139. doi:10.1016/j.molstruc.2009.05.004 |
| 11. | Batchelor, J. G. J. Chem. Soc., Perkin Trans. 2 1976, 1585. doi:10.1039/p29760001585 |
| 12. | Freitas, M. P.; Rittner, R.; Tormena, C. F.; Abraham, R. J. Spectrochim. Acta, Part A 2005, 61, 1771–1776. doi:10.1016/j.saa.2004.07.007 |
| 13. | Freitas, M. P.; Tormena, C. F.; Rittner, R. J. Mol. Struct. 2001, 570, 175–180. doi:10.1016/s0022-2860(01)00482-3 |
| 14. | Basso, E. A.; Abiko, L. A.; Gauze, G. F.; Pontes, R. M. J. Org. Chem. 2011, 76, 145–153. doi:10.1021/jo101819u |
| 20. | Lopes Jesus, A. J.; Rosado, M. T. S.; Redinha, J. S. Comput. Theor. Chem. 2011, 964, 32–39. doi:10.1016/j.comptc.2010.11.031 |
| 22. | Bocca, C. C.; Basso, E. A.; Fiorin, B. C.; Tormena, C. F.; dos Santos, F. P. J. Phys. Chem. A 2006, 110, 9438–9442. doi:10.1021/jp061502n |
| 23. | Basso, E. A.; Kaiser, C.; Rittner, R.; Lambert, J. B. Magn. Reson. Chem. 1994, 32, 205–209. doi:10.1002/mrc.1260320403 |
| 24. | Allinger, N. L.; Pamphilis, N. A. J. Org. Chem. 1973, 38, 316–319. doi:10.1021/jo00942a024 |
| 25. | Yoshida, Z.-i.; Nakagawa, K. Tetrahedron Lett. 1965, 6, 3753–3756. doi:10.1016/s0040-4039(01)99558-9 |
| 26. | Silla, J. M.; Duarte, C. J.; Freitas, M. P.; Ramalho, T. C.; Cormanich, R. A.; Santos, F. P.; Tormena, C. F.; Rittner, R. Spectrochim. Acta, Part A 2011, 81, 359–362. doi:10.1016/j.saa.2011.06.023 |
| 27. | Basso, E. A.; Kaiser, C.; Rittner, R.; Lambert, J. B. J. Org. Chem. 1993, 58, 7865–7869. doi:10.1021/jo00079a035 |
| 28. | Silla, J. M.; Cormanich, R. A.; Duarte, C. J.; Freitas, M. P.; Ramalho, T. C.; Barbosa, T. M.; Santos, F. P.; Tormena, C. F.; Rittner, R. J. Phys. Chem. A 2011, 115, 10122–10127. doi:10.1021/jp206136t |
| 29. | Cedran, J. C.; dos Santos, F. P.; Basso, E. A.; Tormena, C. F. J. Phys. Chem. A 2007, 111, 11701–11705. doi:10.1021/jp075280k |
| 36. | Wittig, G.; Mayer, U. Chem. Ber. 1963, 96, 329–341. doi:10.1002/cber.19630960141 |
| 17. | Alabugin, I. V.; Zeidan, T. A. J. Am. Chem. Soc. 2002, 124, 3175–3185. doi:10.1021/ja012633z |
| 34. | Alabugin, I. V. J. Org. Chem. 2000, 65, 3910–3919. doi:10.1021/jo991622+ |
| 35. | Alabugin, I. V.; Manoharan, M. J. Org. Chem. 2004, 69, 9011–9024. doi:10.1021/jo048287w |
| 43. | NBO 5.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, 2001. |
| 44. | R: A Language and Environment for Statistical Computing, Version 3.5.0; R Foundation for Statistical Computing: Vienna, Austria, 2018. |
| 42. | Hanwell, M. D.; Curtis, D. E.; Lonie, D. C.; Vandermeersch, T.; Zurek, E.; Hutchison, G. R. J. Cheminf. 2012, 4, 17. doi:10.1186/1758-2946-4-17 |
| 33. | Wang, J.; Wolf, R. M.; Caldwell, J. W.; Kollman, P. A.; Case, D. A. J. Comput. Chem. 2004, 25, 1157–1174. doi:10.1002/jcc.20035 |
| 40. | Borch, R. F.; Bernstein, M. D.; Durst, H. D. J. Am. Chem. Soc. 1971, 93, 2897–2904. doi:10.1021/ja00741a013 |
| 37. | Thvedt, T. H. K.; Fuglseth, E.; Sundby, E.; Hoff, B. H. Tetrahedron 2010, 66, 6733–6743. doi:10.1016/j.tet.2010.06.081 |
| 38. | Lautens, M.; Bouchain, G. Org. Synth. 2002, 79, 251. doi:10.15227/orgsyn.079.0251 |
| 39. | Allinger, J.; Allinger, N. L. Tetrahedron 1958, 2, 64–74. doi:10.1016/0040-4020(58)88024-2 |
© 2019 Francisco et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0). Please note that the reuse, redistribution and reproduction in particular requires that the authors and source are credited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (https://www.beilstein-journals.org/bjoc)