Abstract
Superelectrophiles are multiply charged cationic species (dications, trications, etc.) which are characterized by their reactions with weak nucleophiles. These reactive intermediates may also undergo a wide variety of rearrangement-type reactions. Superelectrophilic rearrangements are often driven by charge–charge repulsive effects, as these densely charged ions react so as to maximize the distances between charge centers. These rearrangements involve reaction steps similar to monocationic rearrangements, such as alkyl group shifts, Wagner–Meerwein shifts, hydride shifts, ring opening reactions, and other skeletal rearrangements. This review will describe these types of superelectrophilic reactions.
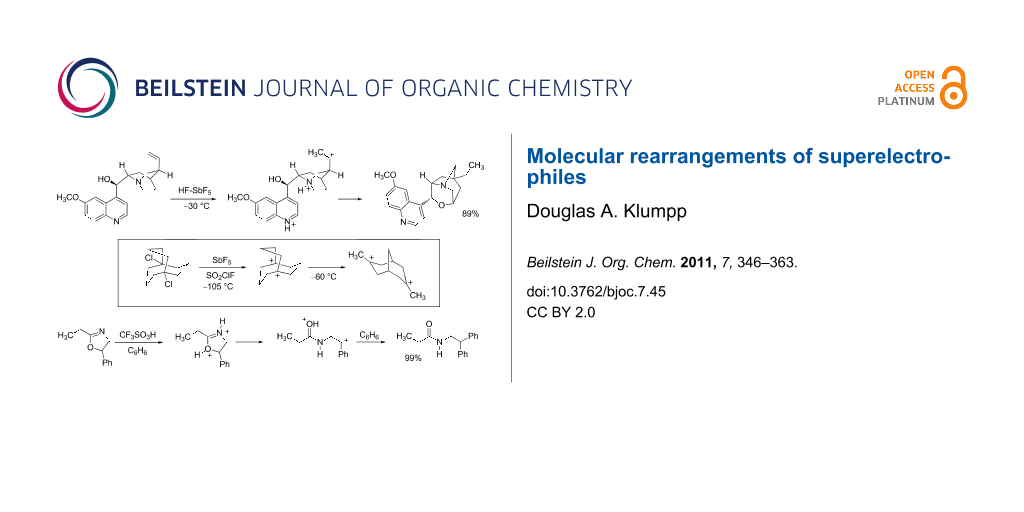
Graphical Abstract
Introduction
The Knorr cyclization is a classical method for preparing quinol-2-ones from β-ketoamides [1]. In 1964, Staskin published a report describing his studies of the Knorr cyclization and noted that the conversion works best with more than 1.0 equiv of Brønsted or Lewis acids [2]. To explain this observation, he suggested a mechanism involving the double protonation of the β-ketoamide to form a dicationic electrophile. A similar mechanism was proposed in which two molecules of Lewis acid were complexed to the β-ketoamide. This manuscript suggested the importance of dicationic intermediates in organic reactions. Other classical conversions, such as the Grewe cyclization [3], clearly involved reactive dicationic intermediates, but until recently there was little or no recognition of these intermediates.
During the 1970s, Brouwer and Kiffin reported [4-6] the reactions of branched alkanes with acetyl cation (CH3CO+) salts in HF·BF3. These studies showed that acetyl cation (CH3CO+) salts were capable of abstracting hydride from the isoalkanes when the reactions were performed in superacdic media. Studies by Olah and coworkers had shown [7] that acetyl cation salts do not react with isoalkanes in aprotic solvents (SO2, SO2ClF, or CH2Cl2). To account for the observed increasing electrophilic reactivities, Olah proposed the concept of superelectrophilic activation [7]. It was suggested that the superacidic media interacts with the non-bonding electron pairs of the acetyl cation (1), to generate a protosolvated superelectrophile (2 or 3, Scheme 1). Protosolvation of the acetyl cation produces an electrophile with increasing dicationic character and consequently superelectrophilic reactivity. Since Olah’s proposal of superelectrophilic activation, the role of dicationic intermediates has become more widely appreciated and it is shown to involve both Brønsted and Lewis acids [8]. Moreover, superelectrophiles have been utilized in many synthetic conversions. While these reactions are often carried out in superacids, less acidic media (CF3CO2H, H2SO4, BF3·H2O, and solid acids) have also been shown to produce superelectrophiles [9-11].
Scheme 1: Superelectrophilic activation of the acetyl cation.
Scheme 1: Superelectrophilic activation of the acetyl cation.
Olah has proposed [8] categories for superelectrophiles, organized according to their structures and the approximate distance between the charge centers (Table 1).
The two basic categories are the gitionic and distonic superelectrophiles. Gitionic (close) superelectrophiles are characterized by the charge centers being separated by no more than one carbon atom or heteroatom. They are further distinguished by the distance between charges: Geminal systems (4 and 5) have the charges located around a single atom whilst vicinal systems (6 and 7) are represented as 1,2-dications. The 1,3-dicationic systems (8 and 9) are also considered gitionic superelectrophiles. It is understood that various factors (including charge delocalization) makes such a classification approximate. Distonic (distant) superelectrophiles are characterized by structures having charges separated by 2 or more carbon atoms or heteroatoms (i.e., 10 and 11). The distonic superelectrophiles are distinguished from other types of onium dications, those in which the onium charge centers are isolated electrophilic sites. In such cases, the onium dications exhibit chemistry that is little different than monocationic electrophiles. Superelectrophiles may also involve hypervalent species, such as protosolvated tert-butyl cation (7).
Superelectrophiles are characterized by several types of reactions [8]. As very powerful electrophiles, they are best known for their reactions with weak nucleophiles, such as arenes and alkanes. This has led to the development of several new synthetic transformations leading to the functionalization of alkanes. Moreover, superelectrophiles have been used to prepare a wide variety of functionalized arenes. Many types of Friedel–Crafts type reactions have been developed. Among the useful Friedel–Crafts reactions, a large number of cyclizations have been developed, including efficient routes to heterocyclic systems [12]. Several reports have also described superelectrophiles participating in concerted reactions, such as the Nazarov cyclization [13]. Because superelectrophiles are often densely charged species, they are also known for their tendencies to undergo rearrangement and charge migration reactions. These types of conversions will be examined in this review article, including ring opening reactions, carbon–carbon bond shifts, skeletal rearrangements, and charge migrations or hydride shifts. Simple Friedel–Crafts type reactions and cyclizations will not be covered.
Review
Ring opening reactions
Several types of superelectrophiles are known to undergo ring opening reactions. The ring opening reaction step can be followed by the reaction with a nucleophile. For example, 2-oxazolines were shown [14] to form products with arenes and a mechanism was proposed involving ring opening of the superelectrophile (13, Scheme 2).
Scheme 2: Ring opening of diprotonated 2-oxazolines.
Scheme 2: Ring opening of diprotonated 2-oxazolines.
The ring opening step effectively separates the positive charge centers, as the superelectrophile isomerizes from a 1,3-dication 13 to a 1,5-dication 14. Subsequent reaction with benzene yields the final product. Using the same chemistry, a chiral 2-oxazoline was shown to give a Friedel–Crafts product in modest diastereoselectivity. A similar reaction was reported [15] in the AlCl3-catalyzed reactions of isoxazolidines (Scheme 3). Product conversion required excess amounts of acid, suggesting a mechanism involving superelectrophile 17. Ring opening to give 18 followed by reaction with benzene afforded 19 in good yield.
Scheme 3: AlCl3-promoted ring opening of isoxaolidine 16.
Scheme 3: AlCl3-promoted ring opening of isoxaolidine 16.
In a similar respect, 2-phenylcyclopropanecarboxylic acid (20) undergoes diprotonation with ring opening to form the distonic superelectrophile 22 (Scheme 4) [16]. Initial protonation is assumed to occur at the carboxylic acid group to produce 21 followed by protonation of the cyclopropyl ring to give 22. Protonation at the C1–C2 bond produces a dicationic species with the largest possible charge separation (1,5-dication). Reaction with benzene and cyclization affords the final product 23. Interestingly, a similar reaction with trans-2- phenylcyclopropylamine hydrochloride 24 leads to cleavage of the C2–C3 bond and formation of the 1,3-dication 25 [17]. Protonation of the C1–C2 bond would provide the 1,4-dication 27, however, this is not observed. It is proposed that the adjacent ammonium group decreases the basicity of the C1–C2 bond in 24, leading to protonation at the more distant C2–C3 bond. The final product is formed by reaction of benzene at the carbocation site.
Scheme 4: Ring-opening reactions of cyclopropyl derivatives.
Scheme 4: Ring-opening reactions of cyclopropyl derivatives.
A number of superelectrophilic ring opening reactions are followed by ring closure steps. For example, ninhydrin (28) was shown [18] to give condensation products with arenes in acid-promoted reactions. In H2SO4, the product 29 is obtained via a simple condensation reaction at the C-2 gem-diol group (Scheme 5). When superacidic CF3SO3H is used, ninhydrin yields 3-(diphenylmethylene)isobenzofuranone (30). If product 29 is isolated and then treated with superacid, 30 is obtained as the sole reaction product.
Scheme 5: Condensations of ninhydrin (28) with benzene.
Scheme 5: Condensations of ninhydrin (28) with benzene.
A mechanism for this conversion is proposed which involves the formation of the O,O-diprotonated superelectrophile 32 with subsequent ring opening and closing reaction steps (Scheme 6). The mechanism can be understood as a consequence of maximizing charge separation and enabling the charge to have resonance stabilization (i.e., 33) with two phenyl rings.
Succinic anhydride (33) reacts in FSO3H-SbF5-SO2ClF solution (Scheme 7) to give the acylium–carboxonium dication 34 which is a stable species at –80 °C [19]. Warming the solution leads to an equilibration between acylium–carboxonium dications and the bis-carboxonium dication.
Scheme 7: Superacid promoted ring opening of succinic anhydride (33).
Scheme 7: Superacid promoted ring opening of succinic anhydride (33).
A similar degenerate rearrangement has also been described for glutaric anhydride in superacid. Phthalic acid (36) also undergoes a dicationic rearrangement via the anhydride (Scheme 8) [20]. Diprotonated phthalic acid 37 is observed by low temperature 1H and 13C NMR. When the solution of 37 is warmed, new signals appear which have been assigned to the cleavage product, the acylium–carboxonium dication 38. NMR evidence suggests the degenerate rearrangement proceeds via the anhydride derivative 39.
Scheme 8: Reaction of phthalic acid (36) in FSO3H-SbF5.
Scheme 8: Reaction of phthalic acid (36) in FSO3H-SbF5.
Carbon migrations and other skeletal rearrangements
Among the reactions of superelectrophiles, a significant number involve the migration of carbon atoms or heteroatoms. For example, ring expansions reactions have been reported for superelectrophiles. In the synthesis of the analgesic drug butorphanol (40) [21], a key step involves the ring expansion of dication 42 to dication 43 (Scheme 9). Interestingly, the ring expansion step moves the carbocationic site away from a benzylic position, but also transforms it from a 1,4-dication to a 1,5-dication. This suggests charge–charge repulsive effects in this system.
Scheme 9: Ring expansion of superelectrophile 42.
Scheme 9: Ring expansion of superelectrophile 42.
When camphor (44) is reacted with HF-SbF5, three products are isolated (Scheme 10) [22]. A mechanism is proposed for conversion of ketone 45 to enone 47. Initially, the carboxonium ion 45a is formed by protonation of the carbonyl oxygen. A second protonation occurs in the superacid to produce the carboxonium-carbonium dication 45b and this species isomerizes to the tertiary-carbenium ion by a Wagner–Meerwein shift. Although this isomerization converts a 1,5-dication to a 1,4-dication, the decreasing charge separation is compensated by the formation of a tertiary-carbenium ion 45c which ultimately leads to the stable enone structure 47.
Scheme 10: Reaction of camphor (44) in superacid.
Scheme 10: Reaction of camphor (44) in superacid.
When 2-cyclohexen-1-one (47) is reacted with HF-SbF5, a ring contraction occurs to give 3-methyl-2-cyclopenten-1-one (50, Scheme 11) [23]. This conversion involves diprotonation of 48 to give a superelectrophile, which undergoes rearrangement via the protonated cyclopropyl derivative 49. Final reaction steps include a hydride shift and deprotonations to give 50.
Scheme 11: Isomerization of 2-cyclohexen-1-one (48).
Scheme 11: Isomerization of 2-cyclohexen-1-one (48).
Jacquesy and coworkers [24] have investigated the chemistry of polycyclic ketones in HF-SbF5-CCl4, a powerful reagent combination for dehydrogenation. For example, 2-decalone (51) (primarily trans) was reacted with HF-SbF5-CCl4 at 0 °C to give products 52 and 53 in 25% and 12% yields, respectively (Scheme 12). The proposed mechanism involves protonation and hydride abstraction to give superelectrophile 54. It is notable that the carbocation forms in the 6- or 7-position on the decalone ring, as this provides maximum separation of the cationic centers. In accord with other carbocation rearrangements, the superelectrophile 54 (a 2° carbocation) isomerizes to 56 (a 3° carbocation). This likely occurs through the ring-fused, protonated cyclopropane 55. Subsequent deprotonation and hydride abstractions steps give the final product 52. A similar series of reactions affords the isomeric product 53.
Scheme 12: Isomerization of 2-decalone (51).
Scheme 12: Isomerization of 2-decalone (51).
An interesting rearrangement and cyclization of an acyl dication has been reported [25]. Ionization of the acid chloride 57 in superacid (FSO3H-SbF5 or HF-SbF5) leads to formation of two ions, 60 and 63, which are observable by NMR spectroscopy (Scheme 13). It was proposed that these ions are formed via superelectrophile 58 by competing hydride and methyl shifts. Following the methyl shift, the acyl cations 61 and 62 are formed. Cyclization then gives the cyclopentenone derivative 63.
Scheme 13: Rearrangement of the acyl-dication 58.
Scheme 13: Rearrangement of the acyl-dication 58.
Carbonylation of superelectrophiles has been shown to give acids and esters in good yields [26]. A rearrangement was described in the carbonylations of dialkyl ketones in HF-SbF5 (Scheme 14). Thus, ketone 64 reacts at 20 °C to give 65–67 as products of carbonylation. At this temperature, the rearrangement product 67 is the major product, whilst at −20 °C compound 65 is the major product. The formation of these products can be understood to be the result of two reactions with the superacid: Protonation of the carbonyl group and protolysis of C–H σ-bonds. As a relatively strong base site, the ketone is completely protonated in the superacid to give the carboxonium ion 68. In the protolysis steps, there is a strong preference to generate the second cationic charge at a site distant from the carboxonium center. Protolysis of the methyl group C–H σ-bonds (i.e., 69) yields superelectrophile 70 by migration of the methyl group. Protolysis also occurs at the methine position (72) which leads directly to superelectrophile 73. Ions 70 and 73 react with carbon monoxide to give products 66 and 65, respectively, on aqueous workup. The major product 67 evidently arises from hydride migration in 70 to give dication 71. This step should be favorable because it increases the distance between charge centers. Although a hydride shift is the most direct route from 70 to 71, this isomerization may also occur through deprotonation and reprotonation steps. As noted by the authors of this study, protolysis steps with alkanes often leads to β-scission reactions (cleavage of the alkane-based carbocations). This reaction path is not observed with superelectrophiles 70, 71, or 73, because these types of cleavage reactions would generate dicationic species with the cationic charges in closer proximity. Consequently, the carboxonium ion has two interesting effects in this superelectrophilic chemistry. It directs protolysis to the most distant site(s) and it “protects” the alkyl chain from cleavage in the superacid.
A series of ozone-based oxidation-rearrangements have been reported by Olah and coworkers some of which involve superelectrophiles [27]. In the presence of Brønsted superacids, ozone is protonated and the resulting ion (O3H+) is a highly reactive electrophilic species, capable of inserting into C–C and C–H σ-bonds in alkanes or alkyl groups. With another ionizable group present in the substrate, dicationic species can be produced. For example, the pentan-1-ol derivative 74 reacts with ozone in magic acid to yield dication 75 quantitatively (Scheme 15). This conversion involves protonation of the hydroxy group to give the oxonium ion 76 and reaction of O3H+ at the methine center of 76. The loss of hydrogen peroxide affords the oxygen-centered cation 78 and subsequent migration of the adjacent group gives dication 75.
Whittaker and Carr have described a series of superacid-promoted reactions to prepare bicyclic lactones [28]. Several of the conversions involve superelectrophilic rearrangements. Ionization of the 1-hydroxy-2-methylcyclohexane carboxylic acid (79) in FSO3H-SO3 at –20 °C leads to a mixture of three ions 80–82 (Scheme 16). For ion 80, a mechanism was proposed which involves initial formation of superelectrophile 83 followed by methyl group migration to produce dication 84 and successive hydride shifts to give 85 which on ring closure affords the protonated lactone 80.
Scheme 16: Rearrangement of 1-hydroxy-2-methylcyclohexane carboxylic acid (79) in superacid.
Scheme 16: Rearrangement of 1-hydroxy-2-methylcyclohexane carboxylic acid (79) in superacid.
A novel isomerization of a bicyclic ring system was described [29] for the 1,5-manxyl dication (87, Scheme 17). Ionization of the dichloride 86 in SbF5-SO2ClF gave the 1,5-manxyl dication (87) which was found to be stable at −105 °C. However, upon warming to −60 °C, the 3,7-dimethylbicyclo[3.3.1]nona-3,7-diyl dication (88) was formed.
Scheme 17: Isomerization of the 1,5-manxyl dication 87.
Scheme 17: Isomerization of the 1,5-manxyl dication 87.
This isomerization is thought to occur through a series of hydride shifts, Wagner–Meerwein shifts, ring contractions, and methyl shifts (Scheme 18). Ab initio calculations were performed and revealed that the isomerization lowers the energy of the dication by about 26 kcal/mol. Moreover, isomerization increased the distance between the carbocation sites from 2.80 Å in 87 to 3.58 Å in 88.
Olah and coworkers have described [30] an attempt to generate the 1,4-dication 90 from the disubstituted 1,4-cyclohexanediol (89, Scheme 19). The 1,4-dication was not stable and instead isomerized to the 1,8-dication 91.
Superelectrophilic carboxonium ions are also known to undergo rearrangements by carbon migrations [31]. For example, Olah and Prakash have described the superacid-promoted isomerization of pivaldehyde (92) to methyl isopropyl ketone (98, Scheme 20).
Scheme 20: Superacid promoted rearrangement of pivaldehyde (92).
Scheme 20: Superacid promoted rearrangement of pivaldehyde (92).
The rearrangement is best carried out in strong or superacidic media (Table 2). Since the carbonyl group is monoprotonated under less acidic conditions, it suggests the involvement of the O,O-diprotonated species 93. Migration of the methyl group leads to separation of the charge centers and the formation of dication 94. Theoretical calculations show that hydride shift for the dications (94 → 95) is energetically unfavorable, presumably due to the closer proximity of the charges. In the final steps, the monocation 96 undergoes a hydride shift to form the carboxonium ion 97 which leads to ketone 98 on deprotonation. Methyl isopropyl ketone (98) is known [32] to be an excellent gasoline oxygenate. Since pivaldehyde can be made from carbon monoxide and isobutane (in superacid), this superelectrophilic rearrangement may have significant commercial value. Other isoalkanes have shown similar chemistry. For example, 3-methylpentane reacts with carbon monoxide to give the isomeric C7 ketones.
Table 2: Isomerization of pivaldehyde in CF3SO3H:CF3CO2H solutionsa.
| H0 | acid system, w/w | pivaldehyde | methyl isopropyl ketone |
|---|---|---|---|
| −10.9 | 26.9% CF3SO3H | 0% | 100% |
| −9.7 | 11.4% CF3SO3H | 17% | 83% |
| −9.4 | 8.0% CF3SO3H | 29% | 71% |
| −8.4 | 3.1% CF3SO3H | 68% | 32% |
| −7.7 | 0.9% CF3SO3H | 83% | 17% |
| −2.7 | 100% CF3SO3H | 100% | 0% |
aReaction conditions: 2 h, 25 °C, 1:5 pivaldehyde:acid.
A retro-pinacol rearrangement is triggered by the superelectrophilic carboxonium 100 and subsequent dehydration leads to the efficient formation of the phenanthrene condensation product 102 (Scheme 21) [33]. The key step involves phenyl migration to the carboxonium carbon. This effectively separates and further stabilizes the carbocationic center. Formation of the 1,2-ethylene dication 101 then gives the cyclization product 102. When dication 101 is generated by other routes, 9,10-diphenylphenanthrene is also formed.
Scheme 21: Rearrangement of a superelectrophilic carboxonium ion 100.
Scheme 21: Rearrangement of a superelectrophilic carboxonium ion 100.
Superelectrophiles are also thought to be involved in some of the classical rearrangements of nitrogen-containing functional groups. For example, Olah and co-workers have studied [34] the Wallach rearrangement and the dicationic intermediates involved were directly observed by low temperature NMR (Scheme 22). Azoxybenzene (103) is shown to form the monoprotonated species 104 in FSO3H at low temperature, while the dicationic species 105 and 106 are directly observable by NMR in HF-SbF5 at low temperature. In the Wallach rearrangement, delocalization of the positive charges is followed by nucleophilic attack by water at a ring carbon during the aqueous workup of the reaction.
Scheme 22: Proposed mechanism for the Wallach rearrangement.
Scheme 22: Proposed mechanism for the Wallach rearrangement.
An interesting example of the Wallach rearrangement was studied by Buncel and coworkers [35]. In a series of reports, they described the reactions of azoxypyridines in sulfuric acid media. The relative reactivities of the α- and β-isomers 108 and 109 were correlated to stabilization of a developing cationic charge center (Scheme 23). Thus, the α-isomer 108 ionizes in 100% H2SO4 to give the tricationic species 110 and subsequent nucleophilic attack gives the product 114. When the β-isomer 104 is reacted under similar conditions, no rearrangement product was obtained. These observations are understood by recognizing that the loss of water from the trications 110 and 115 leads to the development of a positive charge on the adjacent nitrogen atom. In the case of α-isomer 108, the developing azonium cation may be stabilized by resonance interaction with the phenyl group of 111. However, with the β-isomer 109 the developing azonium cation is located next to the pyridinium ring 116. Evidently, structure 116 is destabilized by the unfavorable interactions of cationic charges and the reaction does not occur at a significant rate.
Scheme 23: Wallach rearrangement of azoxypyridines 108 and 109.
Scheme 23: Wallach rearrangement of azoxypyridines 108 and 109.
The benzidine rearrangement is another rearrangement that – depending on the reaction conditions – may involve superelectrophiles [36]. In the reaction of 1,2-diphenylhydrazine (117), the diprotonated species 118 is formed in strong acid and a 5,5-sigmatropic bond migration occurs (Scheme 24). This step involves the isomerization of the 1,2-dication 118 to the 1,10-dication 119, a conversion driven to some extent by charge–charge repulsion. The final deprotonation steps give benzidine 121. Yamabe recently studied the benzidine rearrangement using DFT calculations [37]. The results were in general agreement with the above mechanism: Dication 119 was estimated to be about 9 kcal·mol−1 more stable than dication 118 (calculated ions included 12 molecules of water in their structures). Similarly, Olah and coworkers studied this reaction by low temperature NMR and showed clean conversion of hydrazobenzene to the stable ion 119 in FSO3H-SO3 at –78 °C [34].
Scheme 24: Proposed mechanism of the benzidine rearrangement.
Scheme 24: Proposed mechanism of the benzidine rearrangement.
Jacquesy and coworkers have examined the chemistry of natural products in superacids and found several unusual rearrangements of multiply-protonated species. For example, quinine (122) gives product 123 in 89% yield from reaction with HF-SbF5 at −30 °C (Scheme 25) [38]. The conversion is thought to involve the di- and triprotonated derivatives of quinine 124 and 125. Hydride and Wagner–Meerwein (WM) shifts lead to formation of trication 127. Hydride shift gives trication 128, which undergoes cyclization with the neighboring hydroxy group. This isomerization is somewhat surprising because the 1,4-dicationic system 127 produces a 1,3-dicationic system 128 – generally an energetically unfavorable transformation. This superacid-promoted isomerization of quinine reveals several interesting aspects of the chemistry of structurally complex superelectrophiles. First, protonation of the nitrogen base sites occurs readily and the cationic site may influence the reactivities of adjacent functional groups. This prevents ionization of the hydroxy group and cleavage of the methoxy group, despite being in a superacidic media. Secondly, this example illustrates the challenges in predicting the course of a reaction involving a superelectrophile with a complex structure. There is a very complex interplay of charge–charge repulsions, neighboring group interactions, and other effects.
Scheme 25: Superacid-promoted reaction of quinine (122).
Scheme 25: Superacid-promoted reaction of quinine (122).
A similar type of rearrangement and cyclization was described [39] for the vindoline derivative 130 in HF-SbF5 (Scheme 26). Initial protonation is assumed to occur at the relative strong base sites – the nitrogen atoms and the ester group – to give trication 131. Further protonation of the double bond leads to carbocation 132. This intermediate then undergoes an alkyl group shift and deprotonation to give the rearranged alkene 133. Protonation and charge migration gives ion 135, which cyclizes to afford 136 as a mixture of diastereomers in 18% yield. Like the rearrangement and cyclization of quinine, this reaction of the vindoline derivative 130 involves a series of structurally complex superelectrophiles. Other superacid-promoted reactions of natural products have been described in recent reviews [40,41].
Scheme 26: Superacid-promoted reaction of vindoline derivative 130.
Scheme 26: Superacid-promoted reaction of vindoline derivative 130.
Charge migration or hydride shifts
In the previous section, there were a number of rearrangements that involved both the migration of carbon-centered groups and hydride shifts. The migration of hydride is a common reaction step in carbocation chemistry. Not surprisingly, it also appears to be involved in the chemistry of superelectrophilic systems. There are two means by which charge can migrate in superelectrophiles with the involvement of hydrogen. Charge migration can occur by a direct hydride shift or by deprotonation and protonation steps (Scheme 27). It should be noted that a variety of dicationic superelectrophiles have been shown to exhibit extreme levels of carbon acidity, even undergoing rapid deprotonation in the strongest superacids [42-44]. In general, (di- or tricationic) superelectrophiles tend to favor reactions in which positive charge becomes be more widely dispersed and separated. Reactions are also favored when positive charge can be removed from the structure. Deprotonation can be a means for reducing the overall charge on the superelectrophile. Consequently, the deprotonation–reprotonation may be one of the most common means by which charge migrates in superelectrophiles.
Scheme 27: Charge migration by hydride shift and acid–base chemistry.
Scheme 27: Charge migration by hydride shift and acid–base chemistry.
Several studies have examined this question using deuterium-labeled superelectrophiles. Reaction of 1-hydroxycyclohexanecarboxylic acid (137) in FSO3H and SO3 at −70 °C, followed by warming to 0 °C, gives a clean conversion to the protonated bicyclic lactone 140 (Scheme 28) [28]. A mechanism is proposed which involves ionization to the superelectrophile 138, followed by successive hydride shifts to give the charge separated dication 139. Cyclization then leads to the lactone derivative 140. In order to further probe this conversion, the deuterium labeled compound 141 was prepared and reacted under similar conditions. Interestingly, a lactone derivative was not formed and only the dicationic species 142 was observed by low temperature NMR. It was proposed that the deuterium atoms slow the initial 1,2-hydride (deuteride) shift and charge migration is inhibited.
Scheme 28: Reactions of 1-hydroxycyclohexanecarboxylic acid (137).
Scheme 28: Reactions of 1-hydroxycyclohexanecarboxylic acid (137).
In another study, the heterocyclic alcohol 143 ionizes in superacid to give the 1,4-dication 144 (Scheme 29) [45]. Further reaction steps lead to the 1,5-dication 146 and ultimately to product 147 in 90% yield. With only one deuterium in the final product, this indicates that charge migration has not occurred by hydride (deuteride) shift, but rather via acid–base chemistry. In this case, the acid–base chemistry may be aided by the formation of a conjugated π-system in 145.
Scheme 29: Reaction of alcohol 143 with benzene in superacid.
Scheme 29: Reaction of alcohol 143 with benzene in superacid.
When cationic charges are in close proximity, it is energetically favorable for the charge centers to be further separated. DFT calculations have performed on several systems and charge separation can result in at least 10–20 kcal·mol−1 stabilization. For example, the thiazole derivative 148 was reacted with CF3SO3H and then benzene to give two products (151 and 152, Scheme 30) [42]. When the two precursor superelectrophiles are studied computationally (B3LYP 6-311(d,p) level), the charge separated 1,4-dication 150 is estimated to be about 16 kcal·mol−1 more stable than the 1,3-dication 149. However, since 151 is the major product, this conversion is assumed to be a kinetically controlled reaction. Indeed, compound 152 may be formed exclusively by reacting alcohol 148 in superacid for 1 h, followed by addition of benzene. The initial reaction period enables the superelectrophile to equilibrate and form the more stable charge-separated ion 150. The addition of benzene then forms 152.
Scheme 30: Reaction of alcohol 148 in superacid with benzene.
Scheme 30: Reaction of alcohol 148 in superacid with benzene.
Another recent study included calculations with the solution-phase model MPW1/6-311G(d)//PCMsp and the solvation was found to narrow the energy gap between a superelectrophile and its charge-separated species (Table 3) [45]. By incorporating the solution-phase into the model, the energy gap between the two ions is decreased by between 3–11 kcal·mol−1 compared to gas-phase structures. This result suggests that solvation effects (and almost certainly counter ion effects) are increasingly important in stabilizing superelectrophiles as the ions become more densely charged or the charges are in closer proximity.
Charge migration and hydride shifts have been involved in several synthetic methods involving superelectrophiles. A useful route to aza-polycyclic aromatic compounds has been developed utilizing charge migration [42,45]. For example, alcohol 155 reacts in superacid to give 5-methylbenzo[f]isoquinoline (158, Scheme 31) in good yield. This conversion involves formation of the 1,4-dication 156, which then undergoes charge migration to the 1,5-dication 157. Intramolecular cyclization and benzene elimination gives the benzo[f]isoquinoline system 158.
Scheme 31: Mechanism of aza-polycyclic aromatic compound formation.
Scheme 31: Mechanism of aza-polycyclic aromatic compound formation.
Olah and coworkers have described a series of reactions involving glycols and related substrates in superacids [46]. These substrates are found to give protonated aldehydes and hydride shifts are thought to be involved. In superacidic media, substrates such as ethylene glycol (159) are diprotonated and form the bis-oxonium ions, i.e., 160 as a stable species at −80 °C. When the solution is warmed to 25 °C, protonated acetaldehyde (162) is formed (Scheme 32). The conversion may occur by one of several routes: by dehydration of 160 with formation of the gitionic superelectrophile 161 and hydride shift/proton loss; by a concerted reaction involving loss of hydronium ion and hydride shift via 163; dehydration and proton loss with isomerization of the monocationic species 164. A similar conversion was observed with other substrates such as 1,3-propanediol (165) (Scheme 33) and for alkoxy alcohols, i.e., 169. Both reactions are thought to involve hydride shifts.
Scheme 32: Superacid-promoted reaction of ethylene glycol (159).
Scheme 32: Superacid-promoted reaction of ethylene glycol (159).
Scheme 33: Reactions of 1,3-propanediol (165) and 2-methoxyethanol (169).
Scheme 33: Reactions of 1,3-propanediol (165) and 2-methoxyethanol (169).
Reaction of the 4-chlorobutanoyl cation 172 in superacidic HF-SbF5 or HSO3F-SbF5 leads to formation of the 2-butenoyl cation (175, Scheme 34) [47]. One of the proposed intermediates in this transformation is the superelectrophilic species 174, which undergoes deprotonation to give the 2-butenoyl cation 176. Presumably, 174 is formed by rapid charge migration involving 173. Further evidence for the superelectrophile 174 is obtained from experiments in which the 2-butenoyl cation 175 is generated in DSO3F-SbF5. Significant deuterium incorporation is found at the α and γ positions, suggesting equilibria involving 173–176.
Scheme 34: Rearrangement of superelelctrophilic acyl dication 173.
Scheme 34: Rearrangement of superelelctrophilic acyl dication 173.
Conclusion
As a result of their high charge densities, superelectrophiles can exhibit very high reactivities. Superelectrophilic reactivity extends beyond the realm of chemistry with weak nucleophiles. Superelectrophiles may undergo a variety of rearrangement reactions in order to form more stable structures or to lose positive charge. Typically, stabilized structures are characterized by greater separation of cationic charge centers. Superelectrophiles may also undergo structural rearrangements that lead to favorable deprotonation steps. This gives ions with reduced positive charge. Superelectrophiles have been shown to undergo ring opening reactions, alkyl group shifts, Wagner–Meerwein shifts, and hydride shifts. Thus, superelectrophiles tend to rearrange by reaction steps similar to monocationic rearrangements.
References
-
Knorr, L. Justus Liebigs Ann. Chem. 1886, 236, 69–115. doi:10.1002/jlac.18862360105
Return to citation in text: [1] -
Staskun, B. J. Org. Chem. 1964, 29, 1153–1157. doi:10.1021/jo01028a038
Return to citation in text: [1] -
Palmer, D. C.; Strauss, M. J. Chem. Rev. 1977, 77, 1–36. doi:10.1021/cr60305a003
Return to citation in text: [1] -
Brouwer, D. M.; Kiffen, A. A. Recl. Trav. Chim. Pays-Bas 1973, 92, 689–697. doi:10.1002/recl.19730920617
Return to citation in text: [1] -
Brouwer, D. M.; Kiffen, A. A. Recl. Trav. Chim. Pays-Bas 1973, 92, 809–813. doi:10.1002/recl.19730920716
Return to citation in text: [1] -
Brouwer, D. M.; Kiffen, A. A. Recl. Trav. Chim. Pays-Bas 1973, 92, 906–914. doi:10.1002/recl.19730920812
Return to citation in text: [1] -
Olah, G. A.; Germain, A.; Lin, H. C.; Forsyth, D. A. J. Am. Chem. Soc. 1975, 97, 2928–2929. doi:10.1021/ja00843a067
Return to citation in text: [1] [2] -
Olah, G. A.; Klumpp, D. A. Superelectrophiles and Their Chemistry; Wiley: NY, 2008.
Return to citation in text: [1] [2] [3] -
Prakash, G. K. S.; Mathew, T.; Hoole, D.; Esteves, P. M.; Wang, Q.; Rasul, G.; Olah, G. A. J. Am. Chem. Soc. 2004, 126, 15770–15776. doi:10.1021/ja0465247
Return to citation in text: [1] -
Koltunov, K. Y.; Walspurger, S.; Sommer, J. Chem. Commun. 2004, 1754–1755. doi:10.1039/b404074k
Return to citation in text: [1] -
Klumpp, D. A.; Zhang, Y.; O’Connor, M. J.; Esteves, P. M.; de Almeida, L. S. Org. Lett. 2007, 9, 3085–3088. doi:10.1021/ol0711570
Return to citation in text: [1] -
Klumpp, D. A. ARKIVOC 2009, Part (i) 63–80.
Return to citation in text: [1] -
Suzuki, T.; Ohwada, T.; Shudo, K. J. Am. Chem. Soc. 1997, 119, 6774–6780. doi:10.1021/ja971100g
Return to citation in text: [1] -
Klumpp, D. A.; Rendy, R.; McElrea, A. Tetrahedron Lett. 2004, 45, 7959–7961. doi:10.1016/j.tetlet.2004.08.109
Return to citation in text: [1] -
Seo, Y.; Kim, K. Bull. Korean Chem. Soc. 1995, 16, 356–359.
Return to citation in text: [1] -
Rendy, R.; Zhang, Y.; McElrea, A.; Gomez, A.; Klumpp, D. A. J. Org. Chem. 2004, 69, 2340–2347. doi:10.1021/jo030327t
Return to citation in text: [1] -
Unpublished results.
Return to citation in text: [1] -
Klumpp, D. A.; Fredrick, S.; Lau, S.; Jin, K. K.; Bau, R.; Prakash, G. K. S.; Olah, G. A. J. Org. Chem. 1999, 64, 5152–5155. doi:10.1021/jo990197h
Return to citation in text: [1] -
Olah, G. A.; White, A. M. J. Am. Chem. Soc. 1967, 89, 4752–4756. doi:10.1021/ja00994a032
Return to citation in text: [1] -
Bruck, D.; Rabinovitz, M. J. Am. Chem. Soc. 1977, 99, 240–241. doi:10.1021/ja00443a041
Return to citation in text: [1] -
Kleemann, A.; Engel, J.; Kutscher, B.; Reichert, D. Pharmaceutical Substances, 4th ed.; Thieme: Stuttgart, 2001; p 308.
Return to citation in text: [1] -
Jacquesy, J.-C.; Jacquesy, R.; Patoiseau, J.-F. Tetrahedron 1976, 32, 1699–1704. doi:10.1016/0040-4020(76)85161-7
Return to citation in text: [1] -
Brouwer, D. M.; van Doorn, J. A. Recl. Trav. Chim. Pays-Bas 1971, 90, 1010–1026. doi:10.1002/recl.19710900908
Return to citation in text: [1] -
Martin, A.; Jouannetaud, M.-P.; Jacquesy, J.-C. Tetrahedron Lett. 1996, 37, 7731–7734. doi:10.1016/0040-4039(96)01736-4
Return to citation in text: [1] -
Fărcaşiu, D.; Miller, G.; Sharma, S. J. Phys. Org. Chem. 1990, 3, 639–642. doi:10.1002/poc.610031004
Return to citation in text: [1] -
Yoneda, N.; Sato, H.; Fukuhara, T.; Takahashi, Y.; Suzuki, A. Chem. Lett. 1983, 19–20. doi:10.1246/cl.1983.19
Return to citation in text: [1] -
Olah, G. A.; Yoneda, N.; Ohnishi, R. J. Am. Chem. Soc. 1976, 98, 7341–7345. doi:10.1021/ja00439a038
Return to citation in text: [1] -
Carr, G.; Whittaker, D. J. Chem. Soc., Perkin Trans. 2 1987, 1877–1880. doi:10.1039/p29870001877
Return to citation in text: [1] [2] -
Taeschler, C.; Sorensen, T. S. Tetrahedron Lett. 2001, 42, 5339–5341. doi:10.1016/S0040-4039(01)01032-2
Return to citation in text: [1] -
Olah, G. A.; Prakash, G. K. S.; Rawdah, T. N. J. Am. Chem. Soc. 1980, 102, 6127–6130. doi:10.1021/ja00539a026
Return to citation in text: [1] -
Olah, G. A.; Mathew, T.; Marinez, E. R.; Esteves, P. M.; Etzkorn, M.; Rasul, G.; Prakash, G. K. S. J. Am. Chem. Soc. 2001, 123, 11556–11561. doi:10.1021/ja011253a
Return to citation in text: [1] -
Temple, R. G.; Gribble, N. R. Prepr. Pap. - Am. Chem. Soc., Div. Fuel Chem. 1992, 37, 1829–1835.
Return to citation in text: [1] -
Klumpp, D. A.; Baek, D. N.; Prakash, G. K. S.; Olah, G. A. J. Org. Chem. 1997, 62, 6666–6671. doi:10.1021/jo970293n
Return to citation in text: [1] -
Olah, G. A.; Dunne, K.; Kelly, D. P.; Mo, Y. K. J. Am. Chem. Soc. 1972, 94, 7438–7447. doi:10.1021/ja00776a029
Return to citation in text: [1] [2] -
Buncel, E. Can. J. Chem. 2000, 78, 1251–1271. doi:10.1139/cjc-78-10-1251
Return to citation in text: [1] -
Smith, M. B.; March, J. March’s Advanced Organic Chemistry, 6th ed.; Wiley: NY, 2007; pp 1678–1680.
Return to citation in text: [1] -
Yamabe, S.; Nakata, H.; Yamazaki, S. Org. Biomol. Chem. 2009, 7, 4631–4640. doi:10.1039/b909313c
Return to citation in text: [1] -
Thibaudeau, S.; Violeau, B.; Martin-Mingot, A.; Jouannetaud, M.-P.; Jacquesy, J.-C. Tetrahedron Lett. 2002, 43, 8773–8775. doi:10.1016/S0040-4039(02)02068-3
Return to citation in text: [1] -
Lafitte, C.; Jouannetaud, M.-P.; Jacquesy, J.-C.; Duflos, A. Tetrahedron 1999, 55, 1989–2000. doi:10.1016/S0040-4020(98)01223-X
Return to citation in text: [1] -
Jacquesy, J.-C. In Stable Carbocation Chemistry; Prakash, G. K. S.; Schleyer, P. v. R., Eds.; Wiley: NY, 1997; pp 549–574.
Return to citation in text: [1] -
Jacquesy, J.-C. In Stable Carbocation Chemistry; Olah, G. A.; Prakash, G. K. S., Eds.; Wiley: NY, 2004; pp 359–376.
Return to citation in text: [1] -
Li, A.; Kindelin, P. J.; Klumpp, D. A. Org. Lett. 2006, 8, 1233–1236. doi:10.1021/ol060125u
Return to citation in text: [1] [2] [3] -
Olah, G. A.; Grant, J. L.; Spear, R. J.; Bollinger, J. M.; Serianz, A.; Sipos, G. J. Am. Chem. Soc. 1976, 98, 2501–2507. doi:10.1021/ja00425a018
Return to citation in text: [1] -
Farcasiu, D.; Ghenciu, A. J. Org. Chem. 1991, 56, 6050–6052. doi:10.1021/jo00021a017
Return to citation in text: [1] -
Li, A.; Gilbert, T. M.; Klumpp, D. A. J. Org. Chem. 2008, 73, 3654–3657. doi:10.1021/jo8003474
Return to citation in text: [1] [2] [3] -
Olah, G. A.; Sommer, J. J. Am. Chem. Soc. 1968, 90, 927–933. doi:10.1021/ja01006a016
Return to citation in text: [1] -
Farcasiu, D.; Miller, G. J. Org. Chem. 1989, 54, 5423–5424. doi:10.1021/jo00284a008
Return to citation in text: [1]
| 29. | Taeschler, C.; Sorensen, T. S. Tetrahedron Lett. 2001, 42, 5339–5341. doi:10.1016/S0040-4039(01)01032-2 |
| 30. | Olah, G. A.; Prakash, G. K. S.; Rawdah, T. N. J. Am. Chem. Soc. 1980, 102, 6127–6130. doi:10.1021/ja00539a026 |
| 31. | Olah, G. A.; Mathew, T.; Marinez, E. R.; Esteves, P. M.; Etzkorn, M.; Rasul, G.; Prakash, G. K. S. J. Am. Chem. Soc. 2001, 123, 11556–11561. doi:10.1021/ja011253a |
| 1. | Knorr, L. Justus Liebigs Ann. Chem. 1886, 236, 69–115. doi:10.1002/jlac.18862360105 |
| 7. | Olah, G. A.; Germain, A.; Lin, H. C.; Forsyth, D. A. J. Am. Chem. Soc. 1975, 97, 2928–2929. doi:10.1021/ja00843a067 |
| 16. | Rendy, R.; Zhang, Y.; McElrea, A.; Gomez, A.; Klumpp, D. A. J. Org. Chem. 2004, 69, 2340–2347. doi:10.1021/jo030327t |
| 34. | Olah, G. A.; Dunne, K.; Kelly, D. P.; Mo, Y. K. J. Am. Chem. Soc. 1972, 94, 7438–7447. doi:10.1021/ja00776a029 |
| 4. | Brouwer, D. M.; Kiffen, A. A. Recl. Trav. Chim. Pays-Bas 1973, 92, 689–697. doi:10.1002/recl.19730920617 |
| 5. | Brouwer, D. M.; Kiffen, A. A. Recl. Trav. Chim. Pays-Bas 1973, 92, 809–813. doi:10.1002/recl.19730920716 |
| 6. | Brouwer, D. M.; Kiffen, A. A. Recl. Trav. Chim. Pays-Bas 1973, 92, 906–914. doi:10.1002/recl.19730920812 |
| 38. | Thibaudeau, S.; Violeau, B.; Martin-Mingot, A.; Jouannetaud, M.-P.; Jacquesy, J.-C. Tetrahedron Lett. 2002, 43, 8773–8775. doi:10.1016/S0040-4039(02)02068-3 |
| 3. | Palmer, D. C.; Strauss, M. J. Chem. Rev. 1977, 77, 1–36. doi:10.1021/cr60305a003 |
| 14. | Klumpp, D. A.; Rendy, R.; McElrea, A. Tetrahedron Lett. 2004, 45, 7959–7961. doi:10.1016/j.tetlet.2004.08.109 |
| 36. | Smith, M. B.; March, J. March’s Advanced Organic Chemistry, 6th ed.; Wiley: NY, 2007; pp 1678–1680. |
| 37. | Yamabe, S.; Nakata, H.; Yamazaki, S. Org. Biomol. Chem. 2009, 7, 4631–4640. doi:10.1039/b909313c |
| 8. | Olah, G. A.; Klumpp, D. A. Superelectrophiles and Their Chemistry; Wiley: NY, 2008. |
| 34. | Olah, G. A.; Dunne, K.; Kelly, D. P.; Mo, Y. K. J. Am. Chem. Soc. 1972, 94, 7438–7447. doi:10.1021/ja00776a029 |
| 9. | Prakash, G. K. S.; Mathew, T.; Hoole, D.; Esteves, P. M.; Wang, Q.; Rasul, G.; Olah, G. A. J. Am. Chem. Soc. 2004, 126, 15770–15776. doi:10.1021/ja0465247 |
| 10. | Koltunov, K. Y.; Walspurger, S.; Sommer, J. Chem. Commun. 2004, 1754–1755. doi:10.1039/b404074k |
| 11. | Klumpp, D. A.; Zhang, Y.; O’Connor, M. J.; Esteves, P. M.; de Almeida, L. S. Org. Lett. 2007, 9, 3085–3088. doi:10.1021/ol0711570 |
| 13. | Suzuki, T.; Ohwada, T.; Shudo, K. J. Am. Chem. Soc. 1997, 119, 6774–6780. doi:10.1021/ja971100g |
| 8. | Olah, G. A.; Klumpp, D. A. Superelectrophiles and Their Chemistry; Wiley: NY, 2008. |
| 32. | Temple, R. G.; Gribble, N. R. Prepr. Pap. - Am. Chem. Soc., Div. Fuel Chem. 1992, 37, 1829–1835. |
| 7. | Olah, G. A.; Germain, A.; Lin, H. C.; Forsyth, D. A. J. Am. Chem. Soc. 1975, 97, 2928–2929. doi:10.1021/ja00843a067 |
| 8. | Olah, G. A.; Klumpp, D. A. Superelectrophiles and Their Chemistry; Wiley: NY, 2008. |
| 33. | Klumpp, D. A.; Baek, D. N.; Prakash, G. K. S.; Olah, G. A. J. Org. Chem. 1997, 62, 6666–6671. doi:10.1021/jo970293n |
| 20. | Bruck, D.; Rabinovitz, M. J. Am. Chem. Soc. 1977, 99, 240–241. doi:10.1021/ja00443a041 |
| 18. | Klumpp, D. A.; Fredrick, S.; Lau, S.; Jin, K. K.; Bau, R.; Prakash, G. K. S.; Olah, G. A. J. Org. Chem. 1999, 64, 5152–5155. doi:10.1021/jo990197h |
| 39. | Lafitte, C.; Jouannetaud, M.-P.; Jacquesy, J.-C.; Duflos, A. Tetrahedron 1999, 55, 1989–2000. doi:10.1016/S0040-4020(98)01223-X |
| 19. | Olah, G. A.; White, A. M. J. Am. Chem. Soc. 1967, 89, 4752–4756. doi:10.1021/ja00994a032 |
| 40. | Jacquesy, J.-C. In Stable Carbocation Chemistry; Prakash, G. K. S.; Schleyer, P. v. R., Eds.; Wiley: NY, 1997; pp 549–574. |
| 41. | Jacquesy, J.-C. In Stable Carbocation Chemistry; Olah, G. A.; Prakash, G. K. S., Eds.; Wiley: NY, 2004; pp 359–376. |
| 42. | Li, A.; Kindelin, P. J.; Klumpp, D. A. Org. Lett. 2006, 8, 1233–1236. doi:10.1021/ol060125u |
| 43. | Olah, G. A.; Grant, J. L.; Spear, R. J.; Bollinger, J. M.; Serianz, A.; Sipos, G. J. Am. Chem. Soc. 1976, 98, 2501–2507. doi:10.1021/ja00425a018 |
| 44. | Farcasiu, D.; Ghenciu, A. J. Org. Chem. 1991, 56, 6050–6052. doi:10.1021/jo00021a017 |
| 27. | Olah, G. A.; Yoneda, N.; Ohnishi, R. J. Am. Chem. Soc. 1976, 98, 7341–7345. doi:10.1021/ja00439a038 |
| 47. | Farcasiu, D.; Miller, G. J. Org. Chem. 1989, 54, 5423–5424. doi:10.1021/jo00284a008 |
| 28. | Carr, G.; Whittaker, D. J. Chem. Soc., Perkin Trans. 2 1987, 1877–1880. doi:10.1039/p29870001877 |
| 25. | Fărcaşiu, D.; Miller, G.; Sharma, S. J. Phys. Org. Chem. 1990, 3, 639–642. doi:10.1002/poc.610031004 |
| 42. | Li, A.; Kindelin, P. J.; Klumpp, D. A. Org. Lett. 2006, 8, 1233–1236. doi:10.1021/ol060125u |
| 45. | Li, A.; Gilbert, T. M.; Klumpp, D. A. J. Org. Chem. 2008, 73, 3654–3657. doi:10.1021/jo8003474 |
| 26. | Yoneda, N.; Sato, H.; Fukuhara, T.; Takahashi, Y.; Suzuki, A. Chem. Lett. 1983, 19–20. doi:10.1246/cl.1983.19 |
| 46. | Olah, G. A.; Sommer, J. J. Am. Chem. Soc. 1968, 90, 927–933. doi:10.1021/ja01006a016 |
| 23. | Brouwer, D. M.; van Doorn, J. A. Recl. Trav. Chim. Pays-Bas 1971, 90, 1010–1026. doi:10.1002/recl.19710900908 |
| 42. | Li, A.; Kindelin, P. J.; Klumpp, D. A. Org. Lett. 2006, 8, 1233–1236. doi:10.1021/ol060125u |
| 24. | Martin, A.; Jouannetaud, M.-P.; Jacquesy, J.-C. Tetrahedron Lett. 1996, 37, 7731–7734. doi:10.1016/0040-4039(96)01736-4 |
| 45. | Li, A.; Gilbert, T. M.; Klumpp, D. A. J. Org. Chem. 2008, 73, 3654–3657. doi:10.1021/jo8003474 |
| 21. | Kleemann, A.; Engel, J.; Kutscher, B.; Reichert, D. Pharmaceutical Substances, 4th ed.; Thieme: Stuttgart, 2001; p 308. |
| 28. | Carr, G.; Whittaker, D. J. Chem. Soc., Perkin Trans. 2 1987, 1877–1880. doi:10.1039/p29870001877 |
| 22. | Jacquesy, J.-C.; Jacquesy, R.; Patoiseau, J.-F. Tetrahedron 1976, 32, 1699–1704. doi:10.1016/0040-4020(76)85161-7 |
| 45. | Li, A.; Gilbert, T. M.; Klumpp, D. A. J. Org. Chem. 2008, 73, 3654–3657. doi:10.1021/jo8003474 |
© 2011 Klumpp; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)