Abstract
Molybdenum disulphide (MoS2) is currently regarded as a promising material for the next generation of electronic and optoelectronic devices. However, several issues need to be addressed to fully exploit its potential for field effect transistor (FET) applications. In this context, the contact resistance, RC, associated with the Schottky barrier between source/drain metals and MoS2 currently represents one of the main limiting factors for suitable device performance. Furthermore, to gain a deeper understanding of MoS2 FETs under practical operating conditions, it is necessary to investigate the temperature dependence of the main electrical parameters, such as the field effect mobility (μ) and the threshold voltage (Vth). This paper reports a detailed electrical characterization of back-gated multilayer MoS2 transistors with Ni source/drain contacts at temperatures from T = 298 to 373 K, i.e., the expected range for transistor operation in circuits/systems, considering heating effects due to inefficient power dissipation. From the analysis of the transfer characteristics (ID−VG) in the subthreshold regime, the Schottky barrier height (ΦB ≈ 0.18 eV) associated with the Ni/MoS2 contact was evaluated. The resulting contact resistance in the on-state (electron accumulation in the channel) was also determined and it was found to increase with T as RC proportional to T3.1. The contribution of RC to the extraction of μ and Vth was evaluated, showing a more than 10% underestimation of μ when the effect of RC is neglected, whereas the effect on Vth is less significant. The temperature dependence of μ and Vth was also investigated. A decrease of μ proportional to 1/Tα with α = 1.4 ± 0.3 was found, indicating scattering by optical phonons as the main limiting mechanism for mobility above room temperature. The value of Vth showed a large negative shift (about 6 V) increasing the temperature from 298 to 373 K, which was explained in terms of electron trapping at MoS2/SiO2 interface states.
Introduction
Transition metal dichalcogenides (TMDs) are compound materials formed by the Van der Waals stacking of MX2 layers (where M = Mo, W, etc., i.e., a transition metal, and X = S, Se, Te, i.e., a chalcogen atom). Among the large number of existing layered materials [1], TMDs are currently attracting increasing scientific interest due to some distinct properties, such as the presence of a sizable bandgap in their band structure. As an example, MoS2 (the most studied among TMDs due to its high abundance in nature and relatively high stability under ambient conditions) exhibits an indirect bandgap of ≈1.3 eV in the case of few layers and bulk material and a direct bandgap of ≈1.8 eV in the case of a single layer. These properties make MoS2 an interesting material for the next generation of electronics and optoelectronics devices [2]. As an example, field effect transistors with very interesting performance in terms of the on/off current ratio (106–108) and low subthreshold swing (≈70 meV/decade) have been demonstrated using single [3] and multilayers of MoS2 [4].
MoS2 thin films, obtained either by cleavage from the bulk material or by chemical vapor deposition, are typically unintentionally n-type doped. Since well-assessed methods for doping enrichment of MoS2 under source/drain contacts are still lacking, MoS2 transistors are mostly fabricated by deposition of metals directly on the unintentionally doped material, resulting in the formation of Schottky contacts. Experimental investigations showed that both low work function (e.g., Sc, Ti) and high work function (e.g., Ni, Pt) metals mostly exhibit a Fermi level pinning close to the conduction band of MoS2 [5], resulting in a Schottky barrier height (SBH) for electrons typically ranging from 0.1 to 0.3 eV. The origin of this Fermi level pinning is currently a matter of investigation and a crucial role seems to be played by nanoscale defects/inhomogeneities at the metal/MoS2 interface [6,7].
The presence of this small but not negligible Schottky barrier at source/drain contacts certainly has a strong impact on the electrical characteristics of MoS2 transistors in the subthreshold regime [5]. In addition, the resulting source/drain contact resistance, RC, can also have a significant influence on the electrical properties of the device in the on-state, i.e., above the threshold voltage (Vth). In particular, RC is expected to affect, to some extent, the values of Vth and of the field effect mobility μ extracted from the transfer characteristics (drain current, ID, vs gate bias, VG) of the device and of the on-resistance (Ron) extracted from the output characteristics (drain current, ID, vs drain bias, VDS). Clearly, all these parameters (Vth, μ, and Ron) have their own dependence on the temperature, and their combination results in the device electrical characteristics at a fixed measurement condition. Hence, to gain a deeper understanding of the behavior of MoS2 transistors for real applications, a temperature-dependent characterization of the main electrical parameters under practical operating conditions is mandatory. A temperature range from room temperature to 400 K is a realistic range for device operation in circuits/systems, taking into account the heating effect they undergo due to inefficient heat dissipation. However, to date, only a limited number of papers have focused on the high temperature behavior of MoS2 transistors [8,9].
In this paper, we report a detailed temperature dependent investigation of multilayer MoS2 transistors with Ni source/drain contacts, focusing on the role played by the contact both in the subthreshold regime and above the threshold voltage. In contrast to other literature works, mainly focused on the use of low work function contacts (such as Sc or Ti) to minimize the effect of contact resistance in n-type MoS2 FETs [5], we focused on a high work function metal such as Ni in this paper in order to evaluate the impact of Ni/MoS2 contact resistance on the device field effect mobility μ and threshold voltage Vth. The interest on Ni was also motivated by the recently demonstrated possibility to achieve MoS2 FETs with ambipolar behavior by performing a temperature-bias annealing processes on as-deposited Ni contacts [10]. In the following, the temperature dependence of μ, Vth and RC in the range from 298 to 373 K was determined and the physical mechanisms of these dependences were discussed.
Results and Discussion
Back-gated transistors have been fabricated using multilayer MoS2 flakes (with thickness ranging from ≈40 to ≈50 nm) exfoliated from bulk molybdenite crystals onto a highly doped Si substrate covered with 380 nm thick, thermally grown SiO2. Such relatively thick MoS2 samples have been chosen since it has been reported that the electrical properties (μ, Vth) of simple back-gated transistors fabricated with multilayer MoS2 are much less affected by the effect of the external environment (water/oxygen) [9] with respect to single or few layer devices [11], for which encapsulation is instead required to achieve good electrical performance [3].
Furthermore, as reported in the literature, carrier mobility is only slightly dependent on MoS2 thickness for transistors fabricated on ≈20 to ≈70 nm thick flakes, whereas stronger variations are observed for thinner flakes, with the largest mobility values obtained for thicknesses ranging from 6 to 12 nm [5].
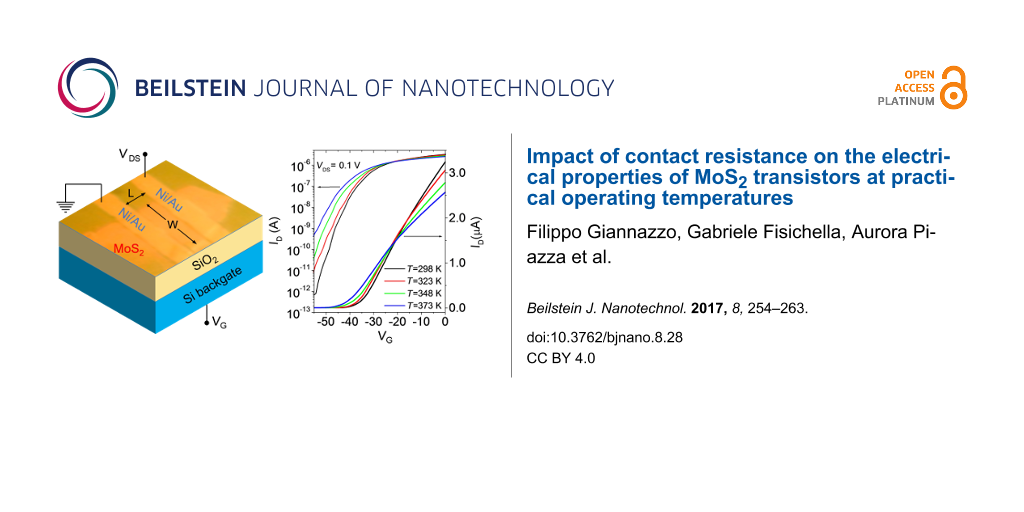
The experiments discussed in this paper have been carried out on a set of ten FETs fabricated on the same substrate. For consistency, the reported temperature-dependent analysis has been carried out on one of the transistors from this set of devices. Figure 1a shows a schematic representation including an optical image of a MoS2 transistor with the SiO2/Si backgate and Ni/Au source and drain contacts. An atomic force microscopy image (Figure 1b) and the corresponding height linescan (Figure 1c) of the MoS2 flake on the SiO2 substrate are also reported, showing ≈40 nm flake thickness.
![[2190-4286-8-28-1]](/bjnano/content/figures/2190-4286-8-28-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: (a) Schematic including an optical image of a MoS2 transistor with the SiO2/Si backgate and Ni/Au source and drain contacts. (b) Atomic force microscopy image and (c) the corresponding height linescan of the MoS2 flake on the SiO2 substrate.
Figure 1: (a) Schematic including an optical image of a MoS2 transistor with the SiO2/Si backgate and Ni/Au s...
The transfer characteristics (ID−VG) measured at a low fixed drain bias (VDS = 0.1 V) on this device at different temperatures from 298 to 373 K are reported in Figure 2 both on a semilogarithmic scale (Figure 2a) and on a linear scale (Figure 2b). Clearly, the linear scale plot allows the current transport above the threshold voltage (Vth) to be studied, whereas the semilog scale plot allows for a better visualization of transport in the subthreshold regime. In the following two sections, a detailed analysis of the characteristics in the subthreshold and above-threshold regime will be reported and the device electrical parameters will be extracted. In particular, the Ni/MoS2 Schottky barrier height and the flat band voltage (VFB) will be evaluated from the temperature-dependent analysis of the subthreshold ID−VG curves, whereas the temperature behavior of Vth and μ will be obtained from the curves above the threshold.
![[2190-4286-8-28-2]](/bjnano/content/figures/2190-4286-8-28-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Semilog scale plot (a) and linear scale plot (b) of the transfer characteristics (ID−VG) measured at a fixed drain bias (VDS = 0.1 V) and at different temperatures ranging from 298 to 373 K. (c) Transconductance (gm = dID/dVG) vs VG curves at different temperatures calculated from the ID−VG characteristics in (b).
Figure 2: Semilog scale plot (a) and linear scale plot (b) of the transfer characteristics (ID−VG) measured a...
Subthreshold behavior
The semilog scale ID−VG characteristics (Figure 2a) measured at 298 K exhibit a current variation of more than six orders of magnitude in the bias range from VG = −55 V to 0 V. This current variation is significantly reduced with increasing the temperature from 298 to 373 K, especially due to the strong increase of current with the temperature at large negative bias.
This is better highlighted in Figure 3a, where the ID−VG characteristics in the gate bias range from −55 to −35 V and at different temperatures from 298 to 373 K have been reported. Such strong dependence of ID on T suggests that current transport in the subthreshold regime is dominated by thermionic current injection through the reverse biased source/MoS2 Schottky contact, according to the relation [5], where ΦB(VG) is the effective Schottky barrier height (SBH), modulated by the gate bias VG. To verify this, for each VG an Arrhenius plot of ID/T2 vs 1000/T is reported in Figure 3b. A nice linear dependence was observed for all the VG in the considered bias range. The effective SBH values ΦB, obtained from the slope of the linear fit of the Arrhenius plot in Figure 3b are reported in Figure 3c as a function of VG. The schematic band diagrams corresponding to the different transistor operation regimes, i.e., depletion (i), flat band (ii) and accumulation (iii), are also illustrated in the inserts of Figure 3c.
![[2190-4286-8-28-3]](/bjnano/content/figures/2190-4286-8-28-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: (a) Semilog scale plot of the transfer characteristics (ID−VG) in the subthreshold regime at different temperatures ranging from 298 to 373 K. (b) Arrhenius plot of ID/T2 vs 1000/T for each gate bias. (c) Effective SBH ΦB as a function of VG. In the inserts, schematic band diagrams are given for the transistor operation in different regimes: depletion (i), flat band voltage (ii) and accumulation (iii).
Figure 3: (a) Semilog scale plot of the transfer characteristics (ID−VG) in the subthreshold regime at differ...
In the depletion regime (Figure 3c (i)), the applied gate bias induces an upward band bending, ψ, in MoS2 at the interface with the SiO2 gate insulator. The experimentally evaluated SBH is found to depend linearly on VG. This dependence can be fitted with the relation where ΦB(VFB) is the effective SBH at the flat band voltage and the term ψ = γ(VG−VFB) is the upward band bending. The slope γ indicates the modulation efficiency of ΦB by the gate bias. It depends on the SiO2 layer capacitance, Cox = ε0εox/tox ≈ 9.1 × 10−5 F/m2 (ε0 is the vacuum dielectric constant, εox = 3.9, tox = 380 nm, the permittivity and the thickness of the SiO2 film, respectively), on the capacitance of the MoS2 depletion region, Cs, as well as on the capacitance associated with MoS2/SiO2 interface traps, Cit [5]. In the depletion regime, the current transport in the transistor is ruled by thermionic emission (TE) of electrons from the source contact to the channel.
The effective SBH ΦB and, hence, the band bending ψ = ΦB(VG)−ΦB(VFB) is found to decrease linearly moving toward positive VG values. The flat band voltage VFB corresponds to the gate bias for which ψ = 0 (see (ii) in Figure 3b), whereas for VG > VFB the band bending ψ < 0 (see (iii) in Figure 3b), i.e., the channel starts to accumulate electrons. In the accumulation regime, current injection in the channel is ruled by thermionic field emission (TFE) through the source triangular barrier. The TFE mechanism yields a reduced effective SBH with respect to the constant ΦB value (red dashed line in Figure 3c) that would be expected if only TE over the barrier would occur. As a guide for the eye, the SBH dependence on VG in the accumulation regime has been fitted with a blue line in Figure 3c. Hence, VFB = −39.6 V can be experimentally determined as the bias corresponding to the intercept between the two linear fits [5]. The corresponding SBH value ΦB(VFB) = 0.18 eV represents the “real” (i.e., gate bias independent) value of the Ni/MoS2 Schottky barrier.
The experimental VFB for the MoS2 transistor exhibits a large negative value, as reported in other literature works [12]. Such a result has been ascribed to donor-like interface trap states (positively charged when empty) between the SiO2 and MoS2 [13,14]. In order to evaluate the amount of this positive charge at the interface, it is worth comparing the experimental value with the one deduced from theoretical expression of the flat band voltage (VFB,id) of an ideal metal-oxide-semiconductor field effect transistor (i.e., without fixed or interface charges). VFB,id is expressed as [15]:
where WM is the work function of the gate material (4.05 eV for the n+-doped Si back gate in our transistor), χ is the semiconductor electron affinity (4.2 eV for MoS2), ND is the semiconductor doping concentration (on the order of 1016 cm−3 in unintentionally doped MoS2) and ni is the intrinsic carrier concentration (for MoS2, cm−3). According to this expression a low value of VFB,id slightly varying with the T (from −0.35 V at 298 K to −0.42 V at 273 K) would be expected for our device. The negative shift of the experimental VFB with respect to VFB,id can be accounted for by the presence of a net positive charge density at the interface with SiO2 that can be evaluated as Cox(VFB−VFB,id)/q ≈ 2.2 × 1012 cm−2.
In the following section, the device transfer characteristics above the threshold will be analyzed to extract the threshold voltage and mobility.
Transfer characteristics above threshold
The linear scale transfer characteristics (Figure 2b) show very low current below a threshold voltage (Vth) and a nearly linear increase of ID vs VG above Vth. Two effects can be observed from the comparison of the ID−VG curves at increasing temperatures, i.e., (i) a negative shift of the threshold voltage and (ii) a decrease of the ID−VG curve slope in the linear region above Vth. The origin of these two effects will be discussed more in detail later on. Interestingly, as a result of these two competing effects, the ID−VG characteristics tend to cross nearly at the same gate bias VG = −21 V (see details in the insert of Figure 2b). This bias condition can be interesting for some applications where it is desirable that the device performance does not depend significantly on the temperature (dID/dT ≈ 0).
Figure 2c shows the transconductance gm vs VG curves calculated by differentiation (gm = dID/dVG) of the ID−VG characteristics in Figure 2b. In the considered bias range, all the curves exhibit an increase of gm with VG up to a maximum value, followed by a decrease of gm. The maximum transconductance value (gm,max) is found to decrease with increasing temperature. Furthermore, a rigid shift of the gm–VG curves toward negative gate bias values is observed with increasing T.
From the linear scale transfer characteristics and the transconductance, two key electrical parameters for transistor operation, i.e., the threshold voltage (Vth) and the field effect mobility (μ), are typically evaluated. Figure 4a shows a linear scale plot of ID (left axis) and of the transconductance gm (right axis) at VDS = 0.1 V and T = 298 K. The field effect mobility in the linear region, μlin, of the transfer characteristics is typically extracted from the transconductance using the following formula where L and W are the channel length and width, respectively, and Cox the SiO2 gate capacitance. For our device with L/W = 7 μm/25 μm and Cox ≈ 9.1 × 10−5 F/m2, the evaluated mobility from the maximum transconductance value gm,max was μlin = 31.75 cm2V−1s−1, as indicated in Figure 4a. A method for evaluating Vth consists of drawing the tangent line to the ID−VG curve at the bias (VG,max) corresponding to gm,max and taking the intercept with the ID = 0 baseline [16], as shown in Figure 4a.
![[2190-4286-8-28-4]](/bjnano/content/figures/2190-4286-8-28-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: (a) Linear scale plot of ID (left axis) and of the transconductance gm (right axis) at VDS = 0.1 V and T = 298 K. The extraction of the field effect mobility (μlin) from the maximum of gm and of Vth by the linear extrapolation method (Vth,lin) is illustrated. (b) Plot of ID/gm1/2 vs VG with illustration of extraction of the mobility (μ0) and threshold voltage value (Vth,0) corrected by the effect of the contact resistance (RC).
Figure 4: (a) Linear scale plot of ID (left axis) and of the transconductance gm (right axis) at VDS = 0.1 V ...
This procedure can be explained by simple geometrical considerations. In the linear region of the transfer characteristics, ID can be expressed as [14]:
Hence, it results that ID,max = gm,max(VG,max−Vth) and the threshold voltage can be calculated as
As a matter of fact, for the evaluation of Vth,lin and μlin based on Equation 2 the contribution of the contact resistance is assumed to be zero. However, as deduced from the analysis of the subthreshold characteristics, a Schottky barrier is associated to the source/drain contacts with MoS2, which is also expected to result in a non-negligible contact resistance, RC. The value of the contact resistance above the threshold and its temperature dependence will be estimated in the last section of this paper from the analysis of the on-resistance (Ron) extracted from the device output characteristics (ID−VDS) at low VDS. Here, we want to discuss how RC can influence the evaluation of μ and Vth from the transfer characteristics.
In order to take into account the role of RC, VDS can be replaced by VDS−IDRC in Equation 2, and solving by ID, the following expression for ID is obtained:
where μ0 and Vth,0 represent the values of the mobility and threshold voltage corrected by the effect of RC. As a consequence, the transconductance gm = dID/dVG can be expressed as:
Noteworthy, the ratio is independent of RC. A plot of ID/gm1/2 vs VG is reported in Figure 4b. The corrected value of the field effect mobility (μ0 = 35.48 ± 0.25 cm2V−1s−1) can be calculated from the slope of the linear fit of these data, whereas the threshold voltage (Vth,0 = −34.99 ± 0.19 V) can be obtained from the intercept with the x axis. It is worth noting that the mobility value μ0 after correction for the contact resistance is more than 10% higher than the value estimated without any correction, whereas the threshold voltage Vth,0 after correction is only 1% higher than the value estimated without accounting for RC. This indicates that the underestimation of the mobility neglecting the contact resistance effect can be quite relevant, whereas the threshold voltage is less affected by RC. By repeating this procedure for all the measured characteristics reported in Figure 2b,c, the temperature dependence of the mobility (μlin and μ0), threshold voltage (Vth and Vth,0) in the considered temperature range has been evaluated, as illustrated in Figure 5a,b, respectively.
![[2190-4286-8-28-5]](/bjnano/content/figures/2190-4286-8-28-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: (a) Temperature dependence of the field effect mobility extracted from the linear region of the ID−VG characteristics without (μlin) and with (μ0) the correction for the effect of the contact resistance RC. Experimental data have been fitted with a temperature dependence 1/Tα. (b) Temperature dependence of the threshold voltage evaluated without (Vth,lin) and with (Vth,0) the correction for the effect of the contact resistance RC. (c) Density of trapped/detrapped electrons at MoS2/SiO2, as a function of T (upper scale) and the corresponding position of the Fermi level with respect to the conduction band (EF−EC).
Figure 5: (a) Temperature dependence of the field effect mobility extracted from the linear region of the ID−V...
Both μlin and μ0 were found to decrease as a function of T with a similar dependence 1/Tα, with α = 1.5 ± 0.2 in the case of μlin and α = 1.4 ± 0.3 in the case of μ0. Such a dependence of μ ≈ 1/Tα with α > 1 indicates that the main mechanism limiting the mobility of electrons in the multilayer MoS2 channel in this temperature range is scattering by optical phonons, as reported by other experimental and theoretical investigations [4]. Instead, electron mobility was found to be limited by Coulomb scattering by charged impurities only at lower temperatures (<100 K) [4]. Noteworthy, scattering by charged impurities at the interface with the substrate results in the dominant mechanism for another well-studied 2D material, graphene, even at room temperature and higher temperatures [17,18].
In Figure 5b, the threshold voltage Vth exhibits a negative shift of about 6 V with increasing the temperature from 298 to 273 K. For convenience, the difference Vth−VFB is also reported in Figure 5b, right scale. It is useful to compare the experimental temperature dependence of Vth with the expected theoretical variation with temperature, in order to understand which are the relevant physical parameters ruling this behavior.
For an ideal transistor (without interface states) operating under accumulation conditions, the shift between the threshold voltage Vth,id and the flat band voltage VFB,id can be expressed as:
where ψth is the downward (negative) band bending at the threshold (as illustrated in the band diagram (iii) of Figure 3c, and Ns(ψth) is the electron density in the channel at ψth
where is the Debye length. The band bending ψth can be evaluated assuming that the electron density in the channel at the threshold corresponds to Ns(ψth) = tND, where ND is the uniform doping concentration in the MoS2 thin film and t its thickness. Assuming ND = 1016 cm−3 for our unintentionally doped MoS2, we obtain Ns ≈ 4 × 1010 cm−2. Furthermore, a value of ψth ranging from approximately −34 meV (at T = 298 K) to −39 meV (at T = 373 K) can be estimated from the dependence of Ns on ψth in Equation 6. Under these assumptions, Vth,id−VFB,id ≈ 0.7 eV (nearly independent of T) can be estimated, as indicated in Figure 5b (blue dashed line).
In order to account for the large change of Vth with temperature, the role of interface states at SiO2/MoS2 interface must be considered. The difference between the experimental Vth−VFB and theoretical Vth,id−VFB,id can be described by a term ΔVit = qNit/Cox, where Nit is the density of trapped/detrapped electrons by SiO2 interface traps. These interface traps exhibit a donor like behavior, i.e., they are positively charged above the Fermi level (when they are empty) and neutral below the Fermi level (when they are filled by electrons) [13]. Hence, electron trapping results in a neutralization of the interface states, resulting in a positive shift of Vth with respect to VFB (i.e. ΔVit > 0). On the contrary, detrapping of electrons from these states results in an increase of the positive charge and, hence, in ΔVit < 0.
From the experimental data in Figure 5b, trapped electron densities Nit = 2 × 1011, 1 × 1011, and 2 × 1010 cm−2 are estimated at 298, 323, and 348 K, respectively, whereas a detrapped electron density Nit = 1.3 × 1011 cm−2 is obtained at 373 K (see Figure 5c). Electron trapping and detrapping at MoS2/SiO2 interface have been shown to be thermally activated processes [13]. Hence, for a given interface trap distribution Dit close to the MoS2 conduction band, Nit can be expressed as
where Ptr(T) and Pdet(T) are the trapping and detrapping probabilities, respectively [13]. The experimentally found temperature dependence of Nit can be explained as follows. As T increases, the shift of the Fermi energy EF with respect to EC increases as
resulting in a change of the integration range in Equation 7. Furthermore, the difference Ptr(T)−Pdet(T) can change with T. The dependence of Nit on EF is also illustrated in Figure 5c. It is consistent with a decrease of Dit with increasing EF−EC. Furthermore, at 373 K, it can be argued that the Pdet becomes higher than Ptr, resulting in a negative value of Nit.
Output characteristics
Figure 6 shows the output characteristics ID−VDS for different gate bias values ranging from VG = −56 to 0 V (with steps ΔV = 4 V) measured at different temperatures, i.e., (a) 298 K, (b) 323 K, (c) 348 K and (d) 373 K. For all the VG values, ID exhibits a linear increase with VDS at low drain bias (VDS << VG−Vth), whereas it deviates from the linear behavior at larger VDS. In particular, current saturation is achieved whenever the condition VDS > VG−Vth is reached. By comparing the output characteristics measured at the different temperatures with the same VG values, it is evident that both the slope of the ID−VDS curves in the linear region and the saturation current value decreases with increasing T.
![[2190-4286-8-28-6]](/bjnano/content/figures/2190-4286-8-28-6.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: Output characteristics ID−VDS for different gate bias values from −56 to 0 V at different temperatures: (a) T = 298 K, (b) T = 323 K, (c) T = 348 K and (d) T = 373 K.
Figure 6: Output characteristics ID−VDS for different gate bias values from −56 to 0 V at different temperatu...
The reciprocal of the ID−VDS curves slope in the linear region at low VDS is the device on-resistance Ron, which can be expressed as:
where RC is the source and drain contact resistance and Rch the channel sheet resistance, which depends inversely on (VG−Vth), according to Equation 2.
Figure 7a reports the plots of Ron vs 1/(VG−Vth,lin) extracted from the ID−VDS characteristics in Figure 6 at the different temperatures. The linear fit of the data was performed for the four temperatures and, from the intercept with the vertical axis, the value of the contact resistance RC was estimated. The behavior of RC vs T is reported in Figure 7b, indicating an increase of RC Tα, with α = 3.1 ± 0.3.
![[2190-4286-8-28-7]](/bjnano/content/figures/2190-4286-8-28-7.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 7: (a) On-resistance Ron vs 1/(VG−Vth,lin) at different temperatures. (b) Temperature dependence of RC.
Figure 7: (a) On-resistance Ron vs 1/(VG−Vth,lin) at different temperatures. (b) Temperature dependence of RC....
Finally, the behavior of the output characteristics at high VDS is discussed. Figure 8a shows the ID−VDS characteristics measured at T = 298 K. The VG−Vth value for each curve is indicated. It can be observed that the current saturation regime (i.e., IDS independent of VDS) is reached only for VG−Vth < 20 V, corresponding to an accumulated electron density in the channel Ns < 1.1 × 1012 cm−2. For VG−Vth > 20 V, saturation is not reached.
![[2190-4286-8-28-8]](/bjnano/content/figures/2190-4286-8-28-8.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 8: (a) Output characteristics (ID−VDS) for different gate bias values from −56 to 0 V at T = 298 K. (b) Plot of ID1/2 vs VG−Vth,lin for VDS = 20 V and linear fit of the data. (c) Saturation mobility μsat vs temperature.
Figure 8: (a) Output characteristics (ID−VDS) for different gate bias values from −56 to 0 V at T = 298 K. (b...
In the saturation condition, ID is only a quadratic function of VG−Vth [14]:
where μsat is the mobility value under saturation conditions and the term B is the so-called body coefficient, which depends on the gate oxide capacitance, on the doping concentration in the film and on the temperature:
For thin gate dielectrics and low doping in the film, B can be approximated to 1, but for thick dielectrics and high doping its value can be significantly higher. In the case of our device with Cox = 9.1 × 10−5 F/m and assuming a MoS2 doping ND ≈ 1 × 1016 cm−3, B can range from ≈2.97 to ≈3.12 in the considered temperature range. In Figure 8b, ID1/2 at VDS = 20 V is reported as a function of VG−Vth, showing a linear behavior. According to Equation 9, the mobility under saturation condition can be evaluated from the slope m of the fit, as . By repeating this procedure for all the output characteristics measured at the different temperatures, the behavior of μsat as a function of T can be obtained. The main error source in the estimation of μsat is related to the fact that the doping concentration ND and, hence, the coefficient B is not exactly known. Noteworthy, the values of μsat in Figure 8c, estimated assuming ND ≈ 1 × 1016 cm−3, are very close to those evaluated from the linear region of the transfer characteristics (see Figure 5a) and exhibit a similar temperature dependence. This also confirms that the assumption for the doping concentration is correct.
Conclusion
In conclusion, a temperature dependent investigation of back-gated multilayer MoS2 transistors with Ni source/drain contacts in the range from T = 298 to 373 K has been performed. The SBH ΦB ≈ 0.18 eV of the Ni/MoS2 contact was evaluated from the analysis of the transfer characteristics ID−VG in the subthreshold regime. The resulting RC associated with the SBH was determined by fitting the Ron dependence on 1/(VG−Vth) extracted from the device output characteristics ID−VDS at low VDS. An increase of RC T3.1 was demonstrated. The impact of RC on the values of μ and Vth values was determined, showing an underestimation of μ by more than 10% if the effect of RC is neglected, whereas the influence of RC on the estimated value of Vth is only 1%. Furthermore, the temperature dependence of μ and Vth was investigated, showing a decrease of μ ≈ 1/Tα with α = 1.4 ± 0.3 (indicating scattering by optical phonons as the limiting mechanism), and a negative shift of Vth by about 6 V with increasing T. The role played by electron trapping at the MoS2/SiO2 interface to explain such a large Vth shift was discussed.
Experimental
Back-gated transistors were fabricated using MoS2 flakes exfoliated from molybdenite bulk crystals (supplier SPI [19]) with thicknesses ranging from ≈40 to ≈50 nm and transferred onto a highly doped n-type Si substrate covered with 380 nm of thermally grown SiO2. An accurate sample preparation protocol has been adopted for controlled quality of the MoS2/SiO2 interface, as this is crucial to achieve reproducible electrical behavior of the devices. In particular, thermo-compression printing using a Karl-Suss nanoimprint device with fixed temperature and pressure conditions [20,21] has been employed to transfer the exfoliated MoS2 flakes onto the SiO2 surface that was previously cleaned using solvents and a soft O2 plasma treatment. Finally, source and drain contacts were obtained by deposition and lift-off of a Ni(50 nm)/Au(100 nm) bilayer.
The temperature-dependent electrical characterization in the range from 298 to 373 K was performed using a Cascade Microtech probe station with an Agilent 4156b parameter analyzer. All the measurements were carried out in dark conditions and under nitrogen flux.
Acknowledgements
P. Fiorenza, I. Deretzis, A. La Magna, C. Bongiorno and G. Nicotra from CNR-IMM are acknowledged for helpful discussions. This work has been supported, in part, by MIUR in the framework of the FlagERA project “GraNitE: Graphene heterostructures with Nitrides for high frequency Electronics” (Grant number 0001411).
References
-
Geim, A. K.; Grigorieva, I. V. Nature 2013, 499, 419–425. doi:10.1038/nature12385
Return to citation in text: [1] -
Wang, Q. H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J. N.; Strano, M. S. Nat. Nanotechnol. 2012, 7, 699–712. doi:10.1038/nnano.2012.193
Return to citation in text: [1] -
Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Nat. Nanotechnol. 2011, 6, 147–150. doi:10.1038/nnano.2010.279
Return to citation in text: [1] [2] -
Kim, S.; Konar, A.; Hwang, W.-S.; Lee, J. H.; Lee, J.; Yang, J.; Jung, C.; Kim, H.; Yoo, J.-B.; Choi, J.-Y.; Jin, Y. W.; Lee, S. Y.; Jena, D.; Choi, W.; Kim, K. Nat. Commun. 2012, 3, No. 1011. doi:10.1038/ncomms2018
Return to citation in text: [1] [2] [3] -
Das, S.; Chen, H.-Y.; Penumatcha, A. V.; Appenzeller, J. Nano Lett. 2013, 13, 100–105. doi:10.1021/nl303583v
Return to citation in text: [1] [2] [3] [4] [5] [6] [7] -
Giannazzo, F.; Fisichella, G.; Piazza, A.; Agnello, S.; Roccaforte, F. Phys. Rev. B 2015, 92, 081307. doi:10.1103/PhysRevB.92.081307
Return to citation in text: [1] -
McDonnell, S.; Addou, R.; Buie, C.; Wallace, R. M.; Hinkle, C. L. ACS Nano 2014, 8, 2880–2888. doi:10.1021/nn500044q
Return to citation in text: [1] -
Jiang, C.; Rumyantsev, S. L.; Samnakay, R.; Shur, M. S.; Balandin, A. A. J. Appl. Phys. 2015, 117, 064301. doi:10.1063/1.4906496
Return to citation in text: [1] -
Kwon, H.-J.; Jang, J.; Kim, S.; Subramanian, V.; Grigoropoulos, C. P. Appl. Phys. Lett. 2014, 105, 152105. doi:10.1063/1.4898584
Return to citation in text: [1] [2] -
Giannazzo, F.; Fisichella, G.; Piazza, A.; Di Franco, S.; Greco, G.; Agnello, S.; Roccaforte, F. Phys. Status Solidi RRL 2016, 10, 797–801. doi:10.1002/pssr.201600209
Return to citation in text: [1] -
Late, D. J.; Liu, B.; Ramakrishna Matte, H. S. S.; Dravid, V. P.; Rao, C. N. R. ACS Nano 2012, 6, 5635–5641. doi:10.1021/nn301572c
Return to citation in text: [1] -
Choi, K.; Raza, S. R. A.; Lee, H. S.; Jeon, P. J.; Pezeshki, A.; Min, S.-W.; Kim, J. S.; Yoon, W.; Ju, S.-Y.; Lee, K.; Im, S. Nanoscale 2015, 7, 5617–5623. doi:10.1039/C4NR06707J
Return to citation in text: [1] -
Guo, Y.; Wei, X.; Shu, J.; Liu, B.; Yin, J.; Guan, C.; Han, Y.; Gao, S.; Chen, Q. Appl. Phys. Lett. 2015, 106, 103109. doi:10.1063/1.4914968
Return to citation in text: [1] [2] [3] [4] -
Park, Y.; Baac, H. W.; Heo, J.; Yoo, G. Appl. Phys. Lett. 2016, 108, 083102. doi:10.1063/1.4942406
Return to citation in text: [1] [2] [3] -
Sze, S. M.; Ng, K. K. Physics of Semiconductor Devices, 3rd ed.; Wiley: New York, 2007.
Return to citation in text: [1] -
Schroder, D. K. Semiconductor Material and Device Characterization, 3rd ed.; Wiley: Hoboken, NJ, 2006.
Return to citation in text: [1] -
Giannazzo, F.; Sonde, S.; Lo Nigro, R.; Rimini, E.; Raineri, V. Nano Lett. 2011, 11, 4612–4618. doi:10.1021/nl2020922
Return to citation in text: [1] -
Sonde, S.; Giannazzo, F.; Vecchio, C.; Yakimova, R.; Rimini, E.; Raineri, V. Appl. Phys. Lett. 2010, 97, 132101. doi:10.1063/1.3489942
Return to citation in text: [1] -
SPI Supplies. http://www.2spi.com (accessed Dec 30, 2016).
Return to citation in text: [1] -
Giannazzo, F.; Fisichella, G.; Piazza, A.; Di Franco, S.; Oliveri, I. P.; Agnello, S.; Roccaforte, F. Mater. Sci. Semicond. Process. 2016, 42, 174–178. doi:10.1016/j.mssp.2015.07.062
Return to citation in text: [1] -
Fisichella, G.; Di Franco, S.; Roccaforte, F.; Ravesi, S.; Giannazzo, F. Appl. Phys. Lett. 2014, 104, 233105. doi:10.1063/1.4882165
Return to citation in text: [1]
| 13. | Guo, Y.; Wei, X.; Shu, J.; Liu, B.; Yin, J.; Guan, C.; Han, Y.; Gao, S.; Chen, Q. Appl. Phys. Lett. 2015, 106, 103109. doi:10.1063/1.4914968 |
| 14. | Park, Y.; Baac, H. W.; Heo, J.; Yoo, G. Appl. Phys. Lett. 2016, 108, 083102. doi:10.1063/1.4942406 |
| 1. | Geim, A. K.; Grigorieva, I. V. Nature 2013, 499, 419–425. doi:10.1038/nature12385 |
| 5. | Das, S.; Chen, H.-Y.; Penumatcha, A. V.; Appenzeller, J. Nano Lett. 2013, 13, 100–105. doi:10.1021/nl303583v |
| 5. | Das, S.; Chen, H.-Y.; Penumatcha, A. V.; Appenzeller, J. Nano Lett. 2013, 13, 100–105. doi:10.1021/nl303583v |
| 4. | Kim, S.; Konar, A.; Hwang, W.-S.; Lee, J. H.; Lee, J.; Yang, J.; Jung, C.; Kim, H.; Yoo, J.-B.; Choi, J.-Y.; Jin, Y. W.; Lee, S. Y.; Jena, D.; Choi, W.; Kim, K. Nat. Commun. 2012, 3, No. 1011. doi:10.1038/ncomms2018 |
| 5. | Das, S.; Chen, H.-Y.; Penumatcha, A. V.; Appenzeller, J. Nano Lett. 2013, 13, 100–105. doi:10.1021/nl303583v |
| 3. | Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Nat. Nanotechnol. 2011, 6, 147–150. doi:10.1038/nnano.2010.279 |
| 3. | Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Nat. Nanotechnol. 2011, 6, 147–150. doi:10.1038/nnano.2010.279 |
| 2. | Wang, Q. H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J. N.; Strano, M. S. Nat. Nanotechnol. 2012, 7, 699–712. doi:10.1038/nnano.2012.193 |
| 5. | Das, S.; Chen, H.-Y.; Penumatcha, A. V.; Appenzeller, J. Nano Lett. 2013, 13, 100–105. doi:10.1021/nl303583v |
| 5. | Das, S.; Chen, H.-Y.; Penumatcha, A. V.; Appenzeller, J. Nano Lett. 2013, 13, 100–105. doi:10.1021/nl303583v |
| 9. | Kwon, H.-J.; Jang, J.; Kim, S.; Subramanian, V.; Grigoropoulos, C. P. Appl. Phys. Lett. 2014, 105, 152105. doi:10.1063/1.4898584 |
| 8. | Jiang, C.; Rumyantsev, S. L.; Samnakay, R.; Shur, M. S.; Balandin, A. A. J. Appl. Phys. 2015, 117, 064301. doi:10.1063/1.4906496 |
| 9. | Kwon, H.-J.; Jang, J.; Kim, S.; Subramanian, V.; Grigoropoulos, C. P. Appl. Phys. Lett. 2014, 105, 152105. doi:10.1063/1.4898584 |
| 11. | Late, D. J.; Liu, B.; Ramakrishna Matte, H. S. S.; Dravid, V. P.; Rao, C. N. R. ACS Nano 2012, 6, 5635–5641. doi:10.1021/nn301572c |
| 5. | Das, S.; Chen, H.-Y.; Penumatcha, A. V.; Appenzeller, J. Nano Lett. 2013, 13, 100–105. doi:10.1021/nl303583v |
| 20. | Giannazzo, F.; Fisichella, G.; Piazza, A.; Di Franco, S.; Oliveri, I. P.; Agnello, S.; Roccaforte, F. Mater. Sci. Semicond. Process. 2016, 42, 174–178. doi:10.1016/j.mssp.2015.07.062 |
| 21. | Fisichella, G.; Di Franco, S.; Roccaforte, F.; Ravesi, S.; Giannazzo, F. Appl. Phys. Lett. 2014, 104, 233105. doi:10.1063/1.4882165 |
| 6. | Giannazzo, F.; Fisichella, G.; Piazza, A.; Agnello, S.; Roccaforte, F. Phys. Rev. B 2015, 92, 081307. doi:10.1103/PhysRevB.92.081307 |
| 7. | McDonnell, S.; Addou, R.; Buie, C.; Wallace, R. M.; Hinkle, C. L. ACS Nano 2014, 8, 2880–2888. doi:10.1021/nn500044q |
| 10. | Giannazzo, F.; Fisichella, G.; Piazza, A.; Di Franco, S.; Greco, G.; Agnello, S.; Roccaforte, F. Phys. Status Solidi RRL 2016, 10, 797–801. doi:10.1002/pssr.201600209 |
| 13. | Guo, Y.; Wei, X.; Shu, J.; Liu, B.; Yin, J.; Guan, C.; Han, Y.; Gao, S.; Chen, Q. Appl. Phys. Lett. 2015, 106, 103109. doi:10.1063/1.4914968 |
| 14. | Park, Y.; Baac, H. W.; Heo, J.; Yoo, G. Appl. Phys. Lett. 2016, 108, 083102. doi:10.1063/1.4942406 |
| 5. | Das, S.; Chen, H.-Y.; Penumatcha, A. V.; Appenzeller, J. Nano Lett. 2013, 13, 100–105. doi:10.1021/nl303583v |
| 12. | Choi, K.; Raza, S. R. A.; Lee, H. S.; Jeon, P. J.; Pezeshki, A.; Min, S.-W.; Kim, J. S.; Yoon, W.; Ju, S.-Y.; Lee, K.; Im, S. Nanoscale 2015, 7, 5617–5623. doi:10.1039/C4NR06707J |
| 13. | Guo, Y.; Wei, X.; Shu, J.; Liu, B.; Yin, J.; Guan, C.; Han, Y.; Gao, S.; Chen, Q. Appl. Phys. Lett. 2015, 106, 103109. doi:10.1063/1.4914968 |
| 13. | Guo, Y.; Wei, X.; Shu, J.; Liu, B.; Yin, J.; Guan, C.; Han, Y.; Gao, S.; Chen, Q. Appl. Phys. Lett. 2015, 106, 103109. doi:10.1063/1.4914968 |
| 4. | Kim, S.; Konar, A.; Hwang, W.-S.; Lee, J. H.; Lee, J.; Yang, J.; Jung, C.; Kim, H.; Yoo, J.-B.; Choi, J.-Y.; Jin, Y. W.; Lee, S. Y.; Jena, D.; Choi, W.; Kim, K. Nat. Commun. 2012, 3, No. 1011. doi:10.1038/ncomms2018 |
| 17. | Giannazzo, F.; Sonde, S.; Lo Nigro, R.; Rimini, E.; Raineri, V. Nano Lett. 2011, 11, 4612–4618. doi:10.1021/nl2020922 |
| 18. | Sonde, S.; Giannazzo, F.; Vecchio, C.; Yakimova, R.; Rimini, E.; Raineri, V. Appl. Phys. Lett. 2010, 97, 132101. doi:10.1063/1.3489942 |
| 14. | Park, Y.; Baac, H. W.; Heo, J.; Yoo, G. Appl. Phys. Lett. 2016, 108, 083102. doi:10.1063/1.4942406 |
| 4. | Kim, S.; Konar, A.; Hwang, W.-S.; Lee, J. H.; Lee, J.; Yang, J.; Jung, C.; Kim, H.; Yoo, J.-B.; Choi, J.-Y.; Jin, Y. W.; Lee, S. Y.; Jena, D.; Choi, W.; Kim, K. Nat. Commun. 2012, 3, No. 1011. doi:10.1038/ncomms2018 |
| 15. | Sze, S. M.; Ng, K. K. Physics of Semiconductor Devices, 3rd ed.; Wiley: New York, 2007. |
| 16. | Schroder, D. K. Semiconductor Material and Device Characterization, 3rd ed.; Wiley: Hoboken, NJ, 2006. |
© 2017 Giannazzo et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Nanotechnology terms and conditions: (http://www.beilstein-journals.org/bjnano)