Abstract
Conformational preferences of the pyrrolidine ring in nucleotide analogs 7–14 were investigated by means of NMR and molecular modeling. The effect of the relative configuration of hydroxy and nucleobase substituents as well as the effect of the alkylation or acylation of the pyrrolidine nitrogen atom on the conformation of the pyrrolidine ring were studied. The results of a conformational analysis show that the alkylation/acylation can be effectively used for tuning the pyrrolidine conformation over the whole pseudorotation cycle.
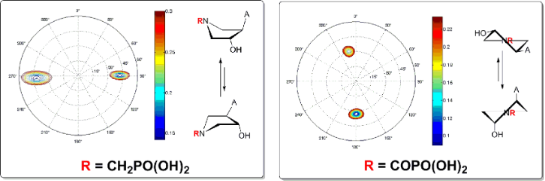
Graphical Abstract
Introduction
Nucleotides, nucleosides and nucleobases play an important role in all biological systems. Therefore, it is not surprising that many of their analogs possess interesting biological properties. Potent antiviral drugs based on phosphonate nucleotides 1a–c [1,2], 2a–d and 3a–d (Figure 1) have been reported. Prodrugs of acyclic compounds 1a–c are currently in clinical use for the treatment of diseases caused by DNA viruses and retroviruses. Cyclic analogs 2 and 3 were reported to exhibit antiviral activity against HIV strains [3]. These examples show that the modification of the sugar-phosphate moiety in nucleotides is a successful approach in developing antiviral therapeutics.
Figure 1: Examples of biologically active acyclic and cyclic nucleotide analogs.
Figure 1: Examples of biologically active acyclic and cyclic nucleotide analogs.
Our long-term interest in the synthesis and evaluation of biological properties of phosphonate azanucleotides has yielded several potent inhibitors of nucleoside/nucleotide metabolizing enzymes: thymine derivatives 4 and 11 (Figure 1 and Figure 2) – inhibitors of thymidine phosphorylase isolated from spontaneous lymphoma of SD rats (IC50 = 15 and 11 nM, respectively) [4], guanine derivative 5 – a potent inhibitor of human purine nucleoside phosphorylase PNP (Ki = 10 nM) [5], and finally guanine derivative 6 – exhibiting inhibitory activity against 6-oxopurine phosphoribosyltransferases from Escherichia coli [6]. These biologically active analogs contain a five-membered pyrrolidine ring, whose conformation has not been explored so far.
It is known that the conformation of a five-membered ribose or deoxyribose ring plays an important role in the nucleoside, nucleotide and oligonucleotide spatial structure. The conformation predefines, for example, the stability of DNA:RNA duplexes – complexes between oligodeoxyribonucleotide and a complementary RNA strain [7] or an overall shape of oligonucleotide. It is also well known that the structure of DNA may alternate between A, B and Z forms depending on the hydration and the type and concentration of metal ions, which is also reflected in the conformation of the sugar part. Finally, the conformation of ribose or its mimics also significantly predetermines the binding of a nucleoside, nucleotide or an analog thereof to an active site of a particular enzyme. The knowledge of the conformation of nucleosides, nucleotides and their analogs is therefore essential for the understanding or even prediction of their biological properties.
There are several approaches providing information on the conformation of a five-membered ring. Conformational analysis using vicinal proton–proton scalar couplings (3JHH) of ring protons obtained from 1H NMR spectra is a traditional and well-established experimental method. 3JHH encodes information on the exocyclic dihedral angle between coupled protons based on the Karplus relationship [8]. Exocyclic dihedral angles are in turn in direct relation with endocyclic dihedral angles between ring atoms defining the conformation of the five-membered ring based on the pseudorotation concept [9]. This straightforward approach is complicated by the presence of more than one rapidly interconverting conformer in solution, resulting in the observation of averaged experimental 3JHH. Nevertheless, even these averaged 3JHH can be used for conformational analysis by means of the program PSEUROT [10], which minimizes differences between experimental and calculated 3JHH, assuming a two-state equilibrium of conformers. The output of the PSEUROT provides pseudorotation parameters: phase angles (P), the maximum puckering amplitudes (Φmax) and the relative amounts of individual conformers. The original PSEUROT program was later complemented with the program MULDER [11]. Recently, the Matlab Pseudorotation GUI version of the program has been developed, enabling the creation of conformational maps [12].
The conformational analysis using PSEUROT-based programs was originally designed for ribose or deoxyribose, but in general it can be used for any saturated five-membered ring. The program PSEUROT was, for example, used in a conformational analysis of the prolyl ring in aminoethylprolyl peptide nucleic acid monomers [13], or in a conformational analysis of 2’-fluoro-4’-thioarabinothymidine [14]. The performance of the Matlab Pseudorotation GUI program was tested on two 4’-thio-2’deoxynucleoside analogs [12].
In this publication, we present a conformational analysis of pyrrolidine azanucleotide analogs 7–14 containing thymine and adenine as examples of pyrimidine and purine nucleobases, respectively (Figure 2), and show how the conformation is affected by the mode of the phosphonate moiety attachment to the pyrrolidine ring. Particularly, we show that the alkylation or acylation (an amine or an amide bond formation) of the pyrrolidine nitrogen atom can be used for a simple but effective tuning of pyrrolidine-ring conformation in compounds 7–14.
Figure 2: The pyrrolidine nucleotide analogs investigated in this study.
Figure 2: The pyrrolidine nucleotide analogs investigated in this study.
Results and Discussion
Chemistry
Phosphonomethyl derivatives 7–10 were prepared from pyrrolidine azanucleosides 15a–d [5,15] via a Mannich-type reaction with diisopropyl phosphite and aqueous formaldehyde at elevated temperature in good yields (Scheme 1). The obtained diisopropyl esters 17a–d were deprotected by treatment with trimethylsilyl bromide in acetonitrile at room temperature.
Scheme 1: The synthesis of pyrrolidine nucleotides 7–14.
Scheme 1: The synthesis of pyrrolidine nucleotides 7–14.
Phosphonoformyl derivatives 11–14 were prepared from 15a–d by the reaction with diisopropyl phenylphosphonoformate (16) at elevated temperature in good yields. The obtained diisopropyl esters 18a–d were deprotected by treatment with trimethylsilyl bromide in acetonitrile at room temperature.
NMR and conformational analysis
Phosphonomethyl 7–10 and phosphonoformyl 11–14 analogs were characterized by 1H, 13C and 31P NMR. The NMR spectra were acquired using 50 mM solutions of the studied compounds in D2O and all resonances were assigned based on H,H-COSY, H,H-ROESY, H,C-HSQC and H,C-HMBC experiments (for a complete signal assignment and copies of NMR spectra, see Supporting Information File 1). The numbering of the pyrrolidine ring, the nucleobase and the endocyclic phase angles Φ0–Φ4 for the purposes of the conformational analysis is shown in Figure 3. There are fundamental differences in the NMR spectra of phosphonomethyl and phosphonoformyl derivatives, which will be commented on in detail in the following paragraphs.
Figure 3: The numbering of the pyrrolidine ring, the nucleobase and the endocyclic phase angles for the purposes of the conformational analysis.
Figure 3: The numbering of the pyrrolidine ring, the nucleobase and the endocyclic phase angles for the purpo...
NMR study of phosphonomethyl derivatives
Phosphonomethyl derivatives 7–10 contain both basic (pyrrolidine) and acidic (phosphonic acid) functionalities. Therefore, several protonation/deprotonation transitions are expected to take place when scanning a pH scale. In order to determine these transitions, we measured NMR spectra of 7–10 at different pD values using D2O solutions of DCl or NaOD for decreasing or increasing pD, respectively. We found that the NMR spectra of 7–10 are strongly pD-dependent as demonstrated for example on the 1H NMR spectrum of adenine derivative 9 (Figure 4).
![[1860-5397-10-205-4]](/bjoc/content/figures/1860-5397-10-205-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: The aliphatic part (pyrrolidine protons) of the 1H NMR spectra of 9 measured in D2O at different pD values.
Figure 4: The aliphatic part (pyrrolidine protons) of the 1H NMR spectra of 9 measured in D2O at different pD...
As follows from pD titrations (Figure 5; for more details see Supporting Information File 1), phosphonomethyl analogs 7–10, both cis (8, 10) and trans (7, 9), exist at a very low pD value (<3) as free phosphonic acids with a deuterated pyrrolidine nitrogen atom (Figure 6). The phosphonic acid moiety goes through a two-stage deuteration/dedeuteration transition at pD ~ 3 and 5 and the pyrrolidine nitrogen atom stays deuterated until pD ~ 9. This suggests that the compounds exist as zwitterions with a hydrogen bond between the negatively charged phosphonate moiety and the positively charged pyrrolidine nitrogen atom in the range of pD 3–9. The pD titration experiments have also revealed the deuteration/dedeuteration of adenine and thymine nucleobases. In agreement with the data reported [16,17], adenine becomes deuterated predominantly on N-1 at pD ~ 3 while thymine releases its deuterium at N-3 at pD ~ 10.5 and becomes negatively charged. Typically, a pD value of 5.7–6.9 was reached when 50 mM solutions of 7–10 in D2O were prepared for the NMR measurement, which indicates that isolated compounds are in the form of the monosodium monozwitterionic salt.
![[1860-5397-10-205-5]](/bjoc/content/figures/1860-5397-10-205-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: Changes of selected 1H and 13C chemical shifts of 9 upon pD change.
Figure 5: Changes of selected 1H and 13C chemical shifts of 9 upon pD change.
Figure 6: The deuteration equilibria of phosphonomethyl derivatives 7–10.
Figure 6: The deuteration equilibria of phosphonomethyl derivatives 7–10.
The orientation of the phosphonomethyl moiety relative to the nucleobase in the zwitterionic form could be theoretically deduced from the H,H-ROESY spectra. In real spectra, however, protons from CH2PO(OH)2 provide NOE contacts to protons on both sides of the pyrrolidine ring, suggesting an exchange of deuterium connected to the pyrrolidine nitrogen.
NMR study of phosphonoformyl derivatives
In contrast to 7–10, an amidic pyrrolidine nitrogen atom in phosphonoformyl derivatives 11–14 is not involved in protonation/deprotonation transitions. Only negligible changes of 1H chemical shifts were observed when the pD value of the solution was changed as demonstrated in the example of compound 13 (Figure 7).
![[1860-5397-10-205-7]](/bjoc/content/figures/1860-5397-10-205-7.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 7: The aliphatic part (pyrrolidine protons) of the 1H NMR spectra of 13 measured in D2O at different pD values.
Figure 7: The aliphatic part (pyrrolidine protons) of the 1H NMR spectra of 13 measured in D2O at different p...
Indeed, the reason is the delocalization of the lone electron pair on the pyrrolidine nitrogen atom by resonance. This brings, in addition to the lack of basicity, the existence of two amide rotamers A and B (Figure 8), which can be observed in NMR spectra as two sets of signals. The ratio of A:B is about 1:1 with a slight excess of rotamer B (see the Experimental and Supporting Information File 1).
Figure 8: Amide rotamers of phosphonoformyl derivatives 11–14.
Figure 8: Amide rotamers of phosphonoformyl derivatives 11–14.
The existence of the two rotamers prompted us to estimate the energy barrier of their interconversion. We therefore performed variable 31P NMR measurements of 14 at different temperatures (starting at 25 °C with a 10 °C step, with the last measurement taken at 100 °C) and a line-shape analysis of an uncoupled, exchanging two-site 31P system (Figure 9). This enabled us to obtain the rate constants of the exchange at different temperatures and estimate the activation parameters of the interconversion such as the Gibbs free energy of activation ΔG‡298 = 80.7 kJ/mol; the enthalpy of activation ΔH‡ = 23.8 kJ/mol; and the entropy of activation ΔS‡ = −190.6 J/(K·mol) (for details, see Supporting Information File 1). The relatively low value of ΔG‡298 = 80.7 kJ/mol implies that the preparative isolation of the individual rotamers A and B at room temperature would not be possible.
![[1860-5397-10-205-9]](/bjoc/content/figures/1860-5397-10-205-9.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 9: The 31P NMR spectra (202.3 MHz) of 14 measured (the black curve) and simulated (the red curve) at various temperatures.
Figure 9: The 31P NMR spectra (202.3 MHz) of 14 measured (the black curve) and simulated (the red curve) at v...
For the purposes of conformational analysis, it was necessary to assign correctly the NMR signals of the individual conformers. We noticed that only one of the C-2’ or C-5’ signals in the particular rotamer is split in the 13C NMR spectrum due to 3J(C,P) spin–spin interaction. In harmony with the general dependence of the vicinal coupling constant on the dihedral angle according to the well-known Karplus relationship, one would expect the 3J(C,P) of the carbon in the trans arrangement to the phosphorus atom to evince larger splitting than the other arranged in the cis arrangement. Thus, 3J(C2’,P) > 3J(C5’,P) in rotamer A and 3J(C5’,P) > 3J(C2’,P) in rotamer B should be observed. In order to support this assumption, we calculated 3J(C,P) of the most stable conformers (see the chapter Conformational analysis) of the adenine derivatives 13 and 14 for both A and B rotamers using the DFT B3LYP/6-31++G* method. The results summarized in Table 1 show a good agreement of the calculated and experimental values, confirming correct assignment of the rotamers (Figure 10).
![[1860-5397-10-205-10]](/bjoc/content/figures/1860-5397-10-205-10.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 10: A part of the H,C-HSQC spectrum of derivative 13, showing the assignment of rotamers A and B.
Figure 10: A part of the H,C-HSQC spectrum of derivative 13, showing the assignment of rotamers A and B.
Conformational analysis
The geometry of the pyrrolidine ring in the compounds studied can occupy various envelope (E) and twisted (T) conformations as depicted in Figure 11. The particular conformation is described by two pseudorotation parameters: by the phase angle (P) and by the maximum puckering amplitude (Φmax) [9]. The phase angle is a periodic variable indicating which ring atoms are situated outside the ring plane and can reach 0°–360°. The maximum puckering amplitude describes the degree of distortion of the five-membered ring out of the plane and its value is usually in the range of 35°–45°.
Figure 11: The pseudorotation pathway of the pyrrolidine ring in the compounds studied. The sign B stands for a nucleobase (thymin-1-yl or adenin-9-yl) and R means a phosphonomethyl or phosphonoformyl moiety.
Figure 11: The pseudorotation pathway of the pyrrolidine ring in the compounds studied. The sign B stands for ...
Conformational analysis using experimental vicinal 1H–1H scalar coupling constants (3JHH) together with PSEUROT-based programs is aimed at fitting the calculated 3JHH to experimental values assuming a two-state conformation equilibrium. In this study, we used the Matlab Pseudorotation GUI program [12] to perform this task. The program requires several input parameters that include experimental 3JHH and constants A and B, describing the relation between exocyclic Φexo (related to 3JHH) and endocyclic Φendo (related to P and Φmax) dihedral angles (Φexo = AΦendo + B).
The values of 3JHH (Table 2) were extracted from the 1H NMR spectra, in which the signals were stereospecifically assigned based on ROESY cross-peaks as demonstrated on the example of compound 14 in Figure 12.
Table 2: The 3JHH of the pyrrolidine-ring protons used in the conformational analysis.
| 2’,3’ | 2”,3’ | 3’,4’ | 4’,5’ | 4’,5” | |
|---|---|---|---|---|---|
| 7 | 6.9 | 6.4 | 4.1 | 5.6 | 9.1 |
| 8 | 2.0 | 5.2 | 6.0 | 6.9 | 9.4 |
| 9 | 6.5 | 5.1 | 3.0 | 4.4 | 7.3 |
| 10 | 3.5 | 6.1 | 6.2 | 5.0 | 7.9 |
| 11A | 6.8 | 4.8 | 5.4 | 6.2 | 7.7 |
| 11B | 6.1 | 5.7 | 5.5 | 6.1 | 8.5 |
| 12A | 2.1 | 5.2 | 4.5 | 9.5 | 8.1 |
| 12B | 3.3 | 4.8 | 4.6 | 8.5 | 8.5 |
| 13A | 6.1 | 4.1 | 4.5 | 5.6 | 6.3 |
| 13B | 5.8 | 5.2 | 5.3 | 5.5 | 7.8 |
| 14A | 2.1 | 5.1 | 4.2 | 9.2 | 7.6 |
| 14B | 3.5 | 4.6 | 4.3 | 8.3 | 8.2 |
![[1860-5397-10-205-12]](/bjoc/content/figures/1860-5397-10-205-12.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 12: An example of the stereospecific assignment of pyrrolidine-ring protons of 14 in the H,H-ROESY spectrum.
Figure 12: An example of the stereospecific assignment of pyrrolidine-ring protons of 14 in the H,H-ROESY spec...
The parameters A and B for the five-membered ribose and deoxyribose ring had been traditionally obtained from X-ray data [18]. In the case of a five-membered ring for which X-ray data are not available, DFT-optimized geometries of a number of conformations are used [19]. This molecular modeling approach was also employed in the case of the studied compounds 7–14. We performed the ring parameterization for adenine derivatives 9, 10, 13 and 14 (see Supporting Information File 1 for details) and assumed that replacing adenine for thymine as a nucleobase would not dramatically affect the constants A and B.
The results of the conformational analysis obtained using the Matlab Pseudorotation GUI program are summarized in Table 3. Instead of presenting the pseudorotation parameters P and Φmax in numbers, we rather present the pseudorotation maps generated by the program in which the contour plots indicate the root-mean-square-deviation between the fitted and experimental 3JHH. These conformation maps provide a more realistic view of the conformational behavior of compounds 7–14 than a single numeric value for P and Φmax.
Table 3: The results of the conformational analysis.
| Analog | Pseudorotation mapa | Conformer populationb | Conformation preferencesc |
|---|---|---|---|
| 7 |
![[Graphic 1]](/bjoc/content/inline/1860-5397-10-205-i2.png?max-width=637&scale=1.0)
|
![[Graphic 2]](/bjoc/content/inline/1860-5397-10-205-i3.png?max-width=637&scale=1.0)
|
|
| 8 |
![[Graphic 4]](/bjoc/content/inline/1860-5397-10-205-i5.png?max-width=637&scale=1.0)
|
![[Graphic 5]](/bjoc/content/inline/1860-5397-10-205-i6.png?max-width=637&scale=1.0)
|
|
| 9 |
![[Graphic 7]](/bjoc/content/inline/1860-5397-10-205-i8.png?max-width=637&scale=1.0)
|
![[Graphic 8]](/bjoc/content/inline/1860-5397-10-205-i9.png?max-width=637&scale=1.0)
|
|
| 10 |
![[Graphic 10]](/bjoc/content/inline/1860-5397-10-205-i11.png?max-width=637&scale=1.0)
|
![[Graphic 11]](/bjoc/content/inline/1860-5397-10-205-i12.png?max-width=637&scale=1.0)
|
|
| 11A |
![[Graphic 13]](/bjoc/content/inline/1860-5397-10-205-i14.png?max-width=637&scale=1.0)
|
![[Graphic 14]](/bjoc/content/inline/1860-5397-10-205-i15.png?max-width=637&scale=1.0)
|
|
| 12A |
![[Graphic 16]](/bjoc/content/inline/1860-5397-10-205-i17.png?max-width=637&scale=1.0)
|
![[Graphic 17]](/bjoc/content/inline/1860-5397-10-205-i18.png?max-width=637&scale=1.0)
|
|
| 13A |
![[Graphic 19]](/bjoc/content/inline/1860-5397-10-205-i20.png?max-width=637&scale=1.0)
|
![[Graphic 20]](/bjoc/content/inline/1860-5397-10-205-i21.png?max-width=637&scale=1.0)
|
|
| 14A |
![[Graphic 22]](/bjoc/content/inline/1860-5397-10-205-i23.png?max-width=637&scale=1.0)
|
![[Graphic 23]](/bjoc/content/inline/1860-5397-10-205-i24.png?max-width=637&scale=1.0)
|
|
aThe contour lines indicate the total RMSD of the fit. bThe contour lines indicate the percentage of the conformation present in the best fit. The thicker black line is the outer contour line of the two dominant conformations from the second column of the table. cA graphical illustration of the conformations obtained from the pseudorotation maps.
The pseudorotation maps reveal the effect of the substitution of the pyrrolidine ring on its conformation. The conformation of phosphonomethyl derivatives 7 and 9 with trans configuration on 3’ and 4’ carbon atoms tends to occupy mainly (~60%) the 1T2 or 1E conformation in an equilibrium with the less populated (~40%) 1E conformer. This equilibrium is significantly shifted in the case of cis derivatives 8 and 10 towards the 2T3 conformation (>80%) due to the steric hindrance of 3’ and 4’ substituents, where the nucleobase occupies predominantly the pseudo-equatorial position. There is an obvious contrast between minor conformations of 8 and 10, which might be caused by hydrogen bonding between the 3’-OH group and the 4’-nucleobase substituent.
A similar effect in the conformer populations was observed for phosphonoformyl derivatives. While trans derivatives 11 and 13 exist as an about 1:1 equilibrium mixture of 3T4 and 3T4 conformations, cis derivatives 12 and 14 prefer (>80%) the 3T4 conformation. The orientation of the phosphonoformyl moiety (rotamers A and B) has a negligible effect on the conformation of the pyrrolidine ring; therefore, only conformation maps for rotamer A are presented in Table 3. The effect of the alkylation or acylation of the pyrrolidine nitrogen is also fairly visible in the pseudorotation maps. Phosphonoformyl derivatives 11–14 keep the conformation of the pyrrolidine ring in narrow northern (P ~ 0°) and southern (P ~ 180°) regions, which arises from the plane arrangement of the C2’–N1’–C5’ fragment of the pyrrolidine ring (minor conformers of cis derivatives 12A and 14A do not follow this trend). In contrast to that, the conformation of the pyrrolidine ring in phosphonomethyl derivatives 7–10 is more flexible and rather occupies the eastern and western segments of the pseudorotation wheel, reacting sensitively to the hydrogen bonding between the 3’-OH group and the 4’-nucleobase substituent.
In order to supplement our experimental observation, we calculated the energy profile of the five-membered pyrrolidine ring pseudorotation for adenine derivatives 9 and 13. We generated 20 conformers covering the whole pseudorotation pathway in 18-degree steps with constant maximum puckering amplitude of 40 degrees. For each conformer, the endocyclic torsion angles Φ0 and Φ3 were kept fixed and the geometry of the molecule was optimized using the DFT B3LYP/6-31G* method in vacuo. Predominant conformations can be found as the energy minima by plotting the calculated energy against phase angle P (Figure 13). The curves in Figure 13 proved a two-state equilibrium used as a prerequisite in PSEUROT-based programs and known for furanose conformation in natural nucleosides and nucleotides.
![[1860-5397-10-205-13]](/bjoc/content/figures/1860-5397-10-205-13.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 13: The energy profile of the five-membered pyrrolidine ring pseudorotation for adenine derivatives 9 and 13.
Figure 13: The energy profile of the five-membered pyrrolidine ring pseudorotation for adenine derivatives 9 a...
The two energy minima were then fully optimized by B3LYP/6-31++G* in water (the CPCM model). The optimized conformations were compared with those obtained by conformational analysis using 3JHH and the results showed a good agreement of the molecular modeling and the experiment (cf. Table 3 and Figure 14).
![[1860-5397-10-205-14]](/bjoc/content/figures/1860-5397-10-205-14.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 14: The most stable conformations of adenine derivatives 9 and 13A calculated by the B3LYP/6-31++G* method in water (CPCM).
Figure 14: The most stable conformations of adenine derivatives 9 and 13A calculated by the B3LYP/6-31++G* met...
Conclusion
In summary, we presented an NMR and DFT conformational analysis of pyrrolidine nucleotide analogs bearing phosphonomethyl or phosphonoformyl substituents attached to the pyrrolidine nitrogen atom. The mode of the phosphonate moiety attachment to the pyrrolidine ring results in tuning the conformation of the five-membered pyrrolidine ring over the whole pseudorotation wheel. While phosphonoformyl derivatives 11–14 keep the conformation of the pyrrolidine ring in narrow northern (P ~ 0°) and southern (P ~ 180°) regions, which arises from the plane arrangement of the C2’–N1’–C5’ fragment of the pyrrolidine ring, the conformation of phosphonomethyl derivatives 7–10 is more flexible and rather occupies the eastern and western segment of the pseudorotation wheel. In general, this simple yet effective tuning of the pyrrolidine-ring conformation can be used for a number of other pyrrolidine derivatives.
Experimental
Chemistry
Phosphonoalkyl derivatives 7–10 were prepared according to the procedures described in [20] while thymine carbonylphosphonic acids 11 and 12 were prepared according to the procedures described in [4]. Unless stated otherwise, all solvents used were anhydrous. TLC was performed on TLC plates precoated with silica gel (silica gel/TLC-cards, UV 254, Merck). The compounds were detected using UV light (254 nm), by spraying with 1% ethanolic solution of ninhydrine to visualize amines, or by spraying with a 1% solution of 4-(4-nitrobenzyl)pyridine in ethanol, followed by heating and treatment with gaseous ammonia (for the detection of alkylating agents, such as dialkyl phosphonates; blue color). The course of the reactions and the purity of the prepared compounds were determined by LC–MS using a Waters AutoPurification System with a 2545 Quaternary Gradient Module and a 3100 Single Quadrupole Mass Detector using a Luna C18 column (100 × 4.6 mm, 3 µm, Phenomenex) at a flow rate of 1 mL/min. The following mobile phase was used, where A, B, and C represent 50 mM NH4HCO3, 50 mM NH4HCO3 in 50% aq CH3CN, and CH3CN, respectively: A→B over 10 min, B→C over 10 min and C for 5 min. Preparative RP HPLC was performed on an LC5000 Liquid Chromatograph (INGOS-PIKRON, CR) using a Luna C18 (2) column (250 × 21.2 mm, 5 µm) at a flow rate of 10 mL/min. A gradient elution of methanol in pH 7.5 0.1 M TEAB (A, 0.1 M TEAB; B, 0.1 M TEAB in 50% aq methanol; C, methanol) was used. All final compounds were lyophilized. Mass spectra were collected on an LTQ Orbitrap XL (Thermo Fisher Scientific) using ESI ionization. The pD titrations were performed on pH meter IQ150 Scientific Instruments equipped with a pH probe PH47-SS. NMR spectra were acquired in D2O on a Bruker AVANCE 600 (1H at 600.1 MHz and 13C at 150.9 MHz), Bruker AVANCE 500 (1H at 499.8 MHz, 13C at 125.7 MHz and 31P at 202.3 MHz) and/or Bruker AVANCE 400 (1H at 400.0 MHz, 13C at 100.6 MHz and 31P at 162.0 MHz) NMR spectrometers. Chemical shifts (in ppm, δ scale) were referenced to the 1,4-dioxane signal (3.75 ppm for 1H and 69.3 ppm for 13C) as an internal or external standard. 31P NMR spectra were referenced to H3PO4 (0 ppm) as an external standard. Coupling constants (J) are given in Hz. The complete assignment of 1H and 13C signals was performed by an analysis of the correlated homonuclear H,H-COSY, H,H-ROESY and heteronuclear H,C-HSQC and H,C-HMBC spectra.
Calculations
All calculations were carried out using the Gaussian 09 software package [21]. DFT calculations were performed using Becke3-LYP [22,23] with 6-31G* basis set for a fixed conformation geometry in the calculation of the energy profile (Figure 13) or 6-31++G* basis set for full geometry optimizations. The full geometry optimizations were carried out using conductor-like polarizable continuum model (CPCM) [24].
General method 1: Synthesis of phosphonoacyl derivatives (13 and 14)
General method 1 followed the similar procedure described previously [6]. The mixture of pyrrolidine nucleosides 15a,b [15] (1 mmol) and diisopropyl phenylphosphonoformiate (1.2 mmol) in DMF (10 mL) was stirred at 80 °C for 1 h (the course of the reaction was followed by TLC using the solvent system H1 (EtOAc/acetone/EtOH/H2O 4:1:1:1) or LC–MS). The reaction mixture was concentrated in vacuo and the intermediate 18a,b was obtained in a pure form by chromatography on silica gel using a linear gradient of H1 in ethyl acetate. The intermediate 18a,b (1 mmol) was dissolved in acetonitrile (10 mL) and bromotrimethylsilane (5 mmol) was added under argon atmosphere. The reaction mixture was stirred overnight at room temperature under argon atmosphere. The reaction mixture was concentrated in vacuo, dissolved in 0.5 M aqueous TEAB (5 mL) and evaporated. The final product was obtained by preparative HPLC, converted to its sodium salt by passing through a column of Dowex 50 in a Na+ form (10 mL/mmol) and lyophilized from water.
(3R,4R)-4-(Adenin-9-yl)-3-hydroxypyrrolidin-1-N-ylcarbonylphosphonic acid (13)
The title compound was prepared according to general method 1 from pyrrolidine nucleoside 15a (0.08 g, 0.36 mmol) in 56% overall yield (75.2 mg, 0.2 mmol) in the form of a white amorphous solid. HRMS–ESI: [M + H]+ calcd for C10H13O5N6NaP, 351.05736; found, 351.05728. The NMR spectra showed a 10:11 mixture of rotamers A:B. Rotamer A: 1H NMR (600.1 MHz, D2O, T = 25 °C, pD = 6.1) 3.54 (dddd, Jgem = 13.6, J2",3' = 4.1, JH,P = 1.9, J2",5" = 0.9, 1H, H-2"), 3.83 (ddd, Jgem = 13.6, J2',3' = 6.1, JH,P = 1.9, 1H, H-2'), 4.55 (ddd, Jgem = 13.0, J5',4' = 5.6, J5',3' = 0.9, 1H, H-5'), 4.57 (ddd, Jgem = 13.0, J5",4' = 6.3, J5",2" = 0.9, 1H, H-5"), 4.73 (dddd, J3',2' = 6.1, J3',4' = 4.5, J3',2" = 4.1, J3',5' = 0.9, 1H, H-3'), 5.01 (ddd, J4',5" = 6.3, J4',5' = 5.6, J4',3' = 4.5, 1H, H-4'), 8.134 (s, 1H, H-8), 8.151 (s, 1H, H-2); 13C NMR (150.9 MHz, D2O, T = 25 °C, pD = 6.1) 51.65 (C-5'), 53.11 (d, JC,P = 4.6, C-2'), 62.87 (C-4'), 73.75 (C-3'), 121.29 (C-5), 142.56 (C-8), 151.58 (C-4), 154.92 (C-2), 157.98 (C-6), 179.15 (d, JC,P = 197.5, P-CO); 31P{1H} NMR (202.3 MHz, D2O, T = 25 °C, pD = 6.1) −2.25. Rotamer B: 1H NMR (600.1 MHz, D2O, T = 25 °C, pD = 6.1) 3.95 (dd, Jgem = 12.6, J2",3' = 5.2, 1H, H-2"), 4.01 (ddd, Jgem = 13.6, J5',4' = 5.5, JH,P = 1.9, 1H, H-5'), 4.19 (ddd, Jgem = 13.6, J5",4' = 7.8, JH,P = 2.0, 1H, H-5"), 4.31 (ddd, Jgem = 12.6, J2',3' = 5.8, J2',5' = 0.8, 1H, H-2'), 4.76 (ddd, J3',2' = 5.8, J3',4' = 5.3, J3',2" = 5.2, 1H, H-3'), 4.99 (ddd, J4',5" = 7.8, J4',5' = 5.5, J4',3' = 5.3, 1H, H-4'), 8.130 (s, 1H, H-8), 8.149 (s, 1H, H-2); 13C NMR (150.9 MHz, D2O, T = 25 °C, pD = 6.1) 50.23 (d, JC,P = 4.9, C-5'), 54.64 (C-2'), 60.88 (C-4'), 75.44 (C-3'), 121.29 (C-5), 142.73 (C-8), 151.62 (C-4), 154.95 (C-2), 158.00 (C-6), 179.24 (d, JC,P = 197.0, P-CO); 31P{1H} NMR (202.3 MHz, D2O, T = 25 °C, pD = 6.1) −2.23.
(3S,4R)-4-(Adenin-9-yl)-3-hydroxypyrrolidin-1-N-ylcarbonylphosphonic acid (14)
The title compound was prepared according to general method 1 from pyrrolidine nucleoside 15b (0.19 g, 0.86 mmol) in 28% overall yield (91 mg, 0.25 mmol) in the form of a white amorphous solid. HRMS–ESI: [M + H]+ calcd for C10H13O5N6NaP, 351.05736; found, 351.05773. The NMR spectra showed a 10:11 mixture of rotamers A:B. Rotamer A: 1H NMR (600.1 MHz, D2O, T = 25 °C, pD = 5.9) 3.65 (dt, Jgem = 13.7, J2',3' = JH,P = 2.1, 1H, H-2'), 3.90 (ddd, Jgem = 13.7, J2",3' = 5.1, JH,P = 1.9, 1H, H-2"), 4.41 (dd, Jgem = 11.6, J5',4' = 9.2, 1H, H-5'), 4.66 (dd, Jgem = 11.6, J5",4' = 7.6, 1H, H-5"), 4.693 (ddd, J3',2" = 5.1, J3',4' = 4.2, J3',2' = 2.1, 1H, H-3'), 5.19 (ddd, J4',5' = 9.2, J4',5" = 7.6, J4',3' = 4.2, 1H, H-4'), 8.158 (s, 1H, H-2), 8.262 (s, 1H, H-8); 13C NMR (150.9 MHz, D2O, T = 25 °C, pD = 5.9) 50.18 (C-5'), 54.30 (d, JC,P = 4.5, C-2'), 58.95 (C-4'), 70.35 (C-3'), 120.80 (C-5), 143.65 (C-8), 151.93 (C-4), 154.89 (C-2), 157.95 (C-6), 178.88 (d, JC,P = 198.3, P-CO); 31P{1H} NMR (202.3 MHz, D2O, T = 25 °C, pD = 5.9) −2.21. Rotamer B: 1H NMR (600.1 MHz, D2O, T = 25 °C, pD = 5.9) 4.04 (ddd, Jgem = 12.8, J5',4' = 8.3, JH,P = 1.9, 1H, H-5'), 4.14 (dd, Jgem = 13.0, J2',3' = 3.5, 1H, H-2'), 4.18 (ddd, Jgem = 12.8, J5",4' = 8.2, JH,P = 1.8, 1H, H-5"), 4.20 (dd, Jgem = 12.6, J2",3' = 4.6, 1H, H-2"), 4.698 (ddd, J3',2" = 4.6, J3',4' = 4.3, J3',2' = 3.5, 1H, H-3'), 5.21 (ddd, J4',5' = 8.3, J4',5" = 8.2, J4',3' = 4.3, 1H, H-4'), 8.163 (s, 1H, H-2), 8.261 (s, 1H, H-8); 13C NMR (150.9 MHz, D2O, T = 25 °C, pD = 5.9) 49.06 (d, JC,P = 5.2, C-5'), 55.63 (C-2'), 57.39 (C-4'), 72.34 (C-3'), 120.82 (C-5), 143.66 (C-8), 152.04 (C-4), 154.90 (C-2), 157.95 (C-6), 178.91 (d, JC,P = 197.9, P-CO); 31P{1H} NMR (202.3 MHz, D2O, T = 25 °C, pD = 5.9) −2.30.
Supporting Information
The pD titration curves of 9 and 10, the variable temperature NMR of 14, the pyrrolidine-ring parameterization for 9, 10, 13 and 14, the NMR signal assignments and copies of the 1H, 13C and 31P NMR spectra are given.
| Supporting Information File 1: Additional experimental data. | ||
| Format: PDF | Size: 1.4 MB | Download |
References
-
De Clercq, E.; Sakuma, T.; Baba, M.; Pauwels, R.; Balzarini, J.; Rosenberg, I.; Holý, A. Antiviral Res. 1987, 8, 261–272. doi:10.1016/S0166-3542(87)80004-9
Return to citation in text: [1] -
Balzarini, J.; Naesens, L.; Herdewijn, P.; Rosenberg, I.; Holý, A.; Pauwels, R.; Baba, M.; Johns, D. G.; De Clercq, E. Proc. Natl. Acad. Sci. U. S. A. 1989, 86, 332–336. doi:10.1073/pnas.86.1.332
Return to citation in text: [1] -
Mackman, R. L.; Boojamra, C. G.; Prasad, V.; Zhang, L.; Lin, K.-Y.; Petrakovsky, O.; Babusis, D.; Chen, J.; Douglas, J.; Grant, D.; Hui, H. C.; Kim, C. U.; Markevitch, D. Y.; Vela, J.; Ray, A.; Cihlar, T. Bioorg. Med. Chem. Lett. 2007, 17, 6785–6789. doi:10.1016/j.bmcl.2007.10.038
Return to citation in text: [1] -
Kočalka, P.; Rejman, D.; Vaněk, V.; Rinnová, M.; Tomečková, I.; Králiková, Š.; Petrová, M.; Páv, O.; Pohl, R.; Buděšínský, M.; Liboska, R.; Točík, Z.; Panová, N.; Votruba, I.; Rosenberg, I. Bioorg. Med. Chem. Lett. 2010, 20, 862–865. doi:10.1016/j.bmcl.2009.12.081
Return to citation in text: [1] [2] -
Rejman, D.; Panová, N.; Klener, P.; Maswabi, B.; Pohl, R.; Rosenberg, I. J. Med. Chem. 2012, 55, 1612–1621. doi:10.1021/jm201409u
Return to citation in text: [1] [2] -
Keough, D. T.; Hocková, D.; Rejman, D.; Špaček, P.; Vrbková, S.; Krečmerová, M.; Eng, W. S.; Jans, H.; West, N. P.; Naesens, L. M. J.; de Jersey, J.; Guddat, L. W. J. Med. Chem. 2013, 56, 6967–6984. doi:10.1021/jm400779n
Return to citation in text: [1] [2] -
Freier, S. M.; Altmann, K.-H. Nucleic Acids Res. 1997, 25, 4429–4443. doi:10.1093/nar/25.22.4429
Return to citation in text: [1] -
Karplus, M. J. Am. Chem. Soc. 1963, 85, 2870–2871. doi:10.1021/ja00901a059
Return to citation in text: [1] -
Altona, C.; Sundaralingam, M. J. Am. Chem. Soc. 1972, 94, 8205–8212. doi:10.1021/ja00778a043
Return to citation in text: [1] [2] -
De Leeuw, F. A. A. M.; Altona, C. J. Comput. Chem. 1983, 4, 428–437. doi:10.1002/jcc.540040319
Return to citation in text: [1] -
Padrta, P.; Sklenář, V. J. Biomol. NMR 2002, 24, 339–349. doi:10.1023/A:1021656808607
Return to citation in text: [1] -
Hendrickx, P. M. S.; Martins, J. C. Chem. Cent. J. 2008, 2, No. 20. doi:10.1186/1752-153X-2-20
Return to citation in text: [1] [2] [3] -
Sharma, N. K.; Ganesh, K. N. Tetrahedron 2010, 66, 9165–9170. doi:10.1016/j.tet.2010.09.082
Return to citation in text: [1] -
Watts, J. K.; Sadalapure, K.; Choubdar, N.; Pinto, B. M.; Damha, M. J. J. Org. Chem. 2006, 71, 921–925. doi:10.1021/jo051844+
Return to citation in text: [1] -
Rejman, D.; Kočalka, P.; Buděšínský, M.; Pohl, R.; Rosenberg, I. Tetrahedron 2007, 63, 1243–1253. doi:10.1016/j.tet.2006.11.047
Return to citation in text: [1] [2] -
Christensen, J. J.; Rytting, J. H.; Izatt, R. M. J. Phys. Chem. 1967, 71, 2700–2705. doi:10.1021/j100867a047
Return to citation in text: [1] -
Christensen, J. J.; Rytting, J. H.; Izatt, R. M. Biochemistry 1970, 9, 4907–4913. doi:10.1021/bi00827a012
Return to citation in text: [1] -
De Leeuw, H. P. M.; Haasnoot, C. A. G.; Altona, C. Isr. J. Chem. 1980, 20, 108–126. doi:10.1002/ijch.198000059
Return to citation in text: [1] -
Houseknecht, J.; Altona, C.; Hadad, C. M.; Lowary, T. L. J. Org. Chem. 2002, 67, 4647–4651. doi:10.1021/jo025635q
Return to citation in text: [1] -
Rejman, D.; Pohl, R.; Kočalka, P.; Masojídková, M.; Rosenberg, I. Tetrahedron 2009, 65, 3673–3681. doi:10.1016/j.tet.2009.02.071
Return to citation in text: [1] -
Gaussian 09, Revision D.01, Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, J., J. A.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; Pople, J. A.; Gaussian, Inc.: Wallingford CT, 2009.
Return to citation in text: [1] -
Becke, A. D. J. Chem. Phys. 1993, 98, 5648–5652. doi:10.1063/1.464913
Return to citation in text: [1] -
Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785–789. doi:10.1103/PhysRevB.37.785
Return to citation in text: [1] -
Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. J. Comput. Chem. 2003, 24, 669–681. doi:10.1002/jcc.10189
Return to citation in text: [1]
| 1. | De Clercq, E.; Sakuma, T.; Baba, M.; Pauwels, R.; Balzarini, J.; Rosenberg, I.; Holý, A. Antiviral Res. 1987, 8, 261–272. doi:10.1016/S0166-3542(87)80004-9 |
| 2. | Balzarini, J.; Naesens, L.; Herdewijn, P.; Rosenberg, I.; Holý, A.; Pauwels, R.; Baba, M.; Johns, D. G.; De Clercq, E. Proc. Natl. Acad. Sci. U. S. A. 1989, 86, 332–336. doi:10.1073/pnas.86.1.332 |
| 6. | Keough, D. T.; Hocková, D.; Rejman, D.; Špaček, P.; Vrbková, S.; Krečmerová, M.; Eng, W. S.; Jans, H.; West, N. P.; Naesens, L. M. J.; de Jersey, J.; Guddat, L. W. J. Med. Chem. 2013, 56, 6967–6984. doi:10.1021/jm400779n |
| 5. | Rejman, D.; Panová, N.; Klener, P.; Maswabi, B.; Pohl, R.; Rosenberg, I. J. Med. Chem. 2012, 55, 1612–1621. doi:10.1021/jm201409u |
| 15. | Rejman, D.; Kočalka, P.; Buděšínský, M.; Pohl, R.; Rosenberg, I. Tetrahedron 2007, 63, 1243–1253. doi:10.1016/j.tet.2006.11.047 |
| 5. | Rejman, D.; Panová, N.; Klener, P.; Maswabi, B.; Pohl, R.; Rosenberg, I. J. Med. Chem. 2012, 55, 1612–1621. doi:10.1021/jm201409u |
| 16. | Christensen, J. J.; Rytting, J. H.; Izatt, R. M. J. Phys. Chem. 1967, 71, 2700–2705. doi:10.1021/j100867a047 |
| 17. | Christensen, J. J.; Rytting, J. H.; Izatt, R. M. Biochemistry 1970, 9, 4907–4913. doi:10.1021/bi00827a012 |
| 4. | Kočalka, P.; Rejman, D.; Vaněk, V.; Rinnová, M.; Tomečková, I.; Králiková, Š.; Petrová, M.; Páv, O.; Pohl, R.; Buděšínský, M.; Liboska, R.; Točík, Z.; Panová, N.; Votruba, I.; Rosenberg, I. Bioorg. Med. Chem. Lett. 2010, 20, 862–865. doi:10.1016/j.bmcl.2009.12.081 |
| 14. | Watts, J. K.; Sadalapure, K.; Choubdar, N.; Pinto, B. M.; Damha, M. J. J. Org. Chem. 2006, 71, 921–925. doi:10.1021/jo051844+ |
| 3. | Mackman, R. L.; Boojamra, C. G.; Prasad, V.; Zhang, L.; Lin, K.-Y.; Petrakovsky, O.; Babusis, D.; Chen, J.; Douglas, J.; Grant, D.; Hui, H. C.; Kim, C. U.; Markevitch, D. Y.; Vela, J.; Ray, A.; Cihlar, T. Bioorg. Med. Chem. Lett. 2007, 17, 6785–6789. doi:10.1016/j.bmcl.2007.10.038 |
| 12. | Hendrickx, P. M. S.; Martins, J. C. Chem. Cent. J. 2008, 2, No. 20. doi:10.1186/1752-153X-2-20 |
| 10. | De Leeuw, F. A. A. M.; Altona, C. J. Comput. Chem. 1983, 4, 428–437. doi:10.1002/jcc.540040319 |
| 12. | Hendrickx, P. M. S.; Martins, J. C. Chem. Cent. J. 2008, 2, No. 20. doi:10.1186/1752-153X-2-20 |
| 9. | Altona, C.; Sundaralingam, M. J. Am. Chem. Soc. 1972, 94, 8205–8212. doi:10.1021/ja00778a043 |
| 13. | Sharma, N. K.; Ganesh, K. N. Tetrahedron 2010, 66, 9165–9170. doi:10.1016/j.tet.2010.09.082 |
| 7. | Freier, S. M.; Altmann, K.-H. Nucleic Acids Res. 1997, 25, 4429–4443. doi:10.1093/nar/25.22.4429 |
| 11. | Padrta, P.; Sklenář, V. J. Biomol. NMR 2002, 24, 339–349. doi:10.1023/A:1021656808607 |
| 18. | De Leeuw, H. P. M.; Haasnoot, C. A. G.; Altona, C. Isr. J. Chem. 1980, 20, 108–126. doi:10.1002/ijch.198000059 |
| 9. | Altona, C.; Sundaralingam, M. J. Am. Chem. Soc. 1972, 94, 8205–8212. doi:10.1021/ja00778a043 |
| 12. | Hendrickx, P. M. S.; Martins, J. C. Chem. Cent. J. 2008, 2, No. 20. doi:10.1186/1752-153X-2-20 |
| 6. | Keough, D. T.; Hocková, D.; Rejman, D.; Špaček, P.; Vrbková, S.; Krečmerová, M.; Eng, W. S.; Jans, H.; West, N. P.; Naesens, L. M. J.; de Jersey, J.; Guddat, L. W. J. Med. Chem. 2013, 56, 6967–6984. doi:10.1021/jm400779n |
| 15. | Rejman, D.; Kočalka, P.; Buděšínský, M.; Pohl, R.; Rosenberg, I. Tetrahedron 2007, 63, 1243–1253. doi:10.1016/j.tet.2006.11.047 |
| 22. | Becke, A. D. J. Chem. Phys. 1993, 98, 5648–5652. doi:10.1063/1.464913 |
| 23. | Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785–789. doi:10.1103/PhysRevB.37.785 |
| 24. | Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. J. Comput. Chem. 2003, 24, 669–681. doi:10.1002/jcc.10189 |
| 4. | Kočalka, P.; Rejman, D.; Vaněk, V.; Rinnová, M.; Tomečková, I.; Králiková, Š.; Petrová, M.; Páv, O.; Pohl, R.; Buděšínský, M.; Liboska, R.; Točík, Z.; Panová, N.; Votruba, I.; Rosenberg, I. Bioorg. Med. Chem. Lett. 2010, 20, 862–865. doi:10.1016/j.bmcl.2009.12.081 |
| 21. | Gaussian 09, Revision D.01, Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, J., J. A.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; Pople, J. A.; Gaussian, Inc.: Wallingford CT, 2009. |
| 19. | Houseknecht, J.; Altona, C.; Hadad, C. M.; Lowary, T. L. J. Org. Chem. 2002, 67, 4647–4651. doi:10.1021/jo025635q |
| 20. | Rejman, D.; Pohl, R.; Kočalka, P.; Masojídková, M.; Rosenberg, I. Tetrahedron 2009, 65, 3673–3681. doi:10.1016/j.tet.2009.02.071 |
© 2014 Poštová Slavětínská et al; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)








