Abstract
Fifteen cyclic and acylic carbenes have been calculated with density functional theory at the BP86/def2-TZVPP level. The strength of the internal X→p(π) π-donation of heteroatoms and carbon which are bonded to the C(II) atom is estimated with the help of NBO calculations and with an energy decomposition analysis. The investigated molecules include N-heterocyclic carbenes (NHCs), the cyclic alkyl(amino)carbene (cAAC), mesoionic carbenes and ylide-stabilized carbenes. The bonding analysis suggests that the carbene centre in cAAC and in diamidocarbene have the weakest X→p(π) π-donation while mesoionic carbenes possess the strongest π-donation.
Graphical Abstract
Introduction
Since the isolation and unambiguous characterization of imidazol-2-ylidene by Arduengo in 1991 [1], the chemistry of stable singlet carbenes has become a major field of chemical research [2-4]. The outstanding stability and synthetic utility of N-heterocyclic carbenes (NHCs) is an ongoing subject to an ubiquitous number of experimental and computational studies exploring their structural and electronic properties [5-8]. In the last two decades, these versatile compounds have been widely employed in transition metal [9-13] and organocatalysis [14-16], organometallic [17-19] and main group synthesis [20-26], and activation of small molecules [27,28].
NHCs possess a divalent C(II) atom which is connected to one or two nitrogen atoms [2,29]. The adjacent heteroatoms stabilize the singlet form by both their σ-electron-withdrawing character and the π-electron-donation of their lone pairs into the formally empty 2p orbital of C(II), giving rise to a four π-electron three-centre system [1,2,30,31]. Thus, the lone pair placed in the plane of the ring renders NHCs as nucleophilic compounds while the partially empty 2p orbital on Ccarb provides some π-acceptor character. It has been initially claimed that the excellent ligand features of NHCs were due to their strong σ-donation abilities [32,33]. However, experimental and computational evidences have revealed non-negligible π-acceptor properties [34-38]. In recent years, several strategies have successfully been developed for tuning the π-acidity of NHCs by changing substitution and structural patterns, such as the size of the backbone ring [39-41], variation of the α-heteroatoms [7], anti-Bredt NHCs [42,43], mesoionic NHCs [44-47], ylide stabilized carbenes [48-51] and other [52-55]. A remarkable variation was introduced with the cyclic alkyl(amino)carbene (cAAC) by Bertrand in 2005 [20,56,57]. The replacement of one amino substituent by a saturated alkyl group makes the carbene more nucleophilic and electrophilic at the same time [20,56,57]. Since then, cAACs have been used as a superior ligand for the stabilization of unstable chemical species, radical and main group elements in different oxidation states [27,34,36,58-60], due to their stronger π-acceptor and σ-donor properties.
With such a wide range of NHCs, a thorough knowledge of the electronic nature is a prerequisite for a guided design of suitable applications. In this regard, a number of techniques have been developed to quantify the π-acceptor ability of carbenes [61,62]. Thus, NMR methods have been reported that allow the measurement of the π-acidity of NHCs [63]. Bertrand et al. and Ganter et al. have proposed the use of 31P and 77Se NMR chemical shift of the NHC-phenylphosphinidene and NHC-selenium adducts, respectively, to determine the π-acceptor strength of the parent NHCs [64,65]. In the same way, Nolan et al. have applied this technique to a wider range of NHCs and have established the connection between the π-accepting abilities and the NMR chemical shift [66]. Furthermore, different theoretical approaches can be found in the literature where natural bond orbital calculations (NBO) and energy decomposition analysis (EDA) have been applied to a broad variety of organometallic complexes [35,67-72]. Although all the procedures have proven to be a convenient way to evaluate the π-acceptor capacities of NHCs, they are limited by the fact that they inherently estimate properties of the parents systems after complexation. It would be helpful if the intrinsic π-donor strength of the substituents to the carbene centre would be directly estimated in the parent carbenes.
In the quest of a direct estimate of the NHC π-acceptor properties and its connection with the π-stabilization exerted by the adjacent α-heteroatoms to the carbene carbon atom, herein we report on the use of the EDA-NOCV (energy decomposition analysis with natural orbitals for chemical valence) method to evaluate the intrinsic electronic π-donation strength. In this context, we quantitatively estimate the differences in the electronic structure of 15 archetypical carbenes (Scheme 1). Here compounds 1–4, 6, and 7 are typical NHCs while 5 is an acylic diamidocarbene. Compounds 8–10 are so-called abnormal or mesoionic carbenes for which no resonance form without formal charges can be written [73]. Molecules 11 and 12 are NHCs with one nitrogen donor atom where the carbene centre is additionally stabilised by another hetero π-donor. Compounds 13 and 14 are ylide-stabilised carbenes while 15 is a diamidocarbene.
Scheme 1: Schematic view of the calculated carbenes 1–15.
Scheme 1: Schematic view of the calculated carbenes 1–15.
Computational Details
All geometries were optimized without symmetry constraint within the DFT framework using the BP86 functional [74,75] in combination with the Gaussian basis sets def2-TZVPP [76]. Stationary points were located with the Berny algorithm [77] using redundant coordinates. Analytical Hessians were computed to determinate the nature of the stationary points [78]. All geometry optimization computations were performed using the Gaussian 09 suite of programs [79]. Wiberg Bond Orders [80] and NPA [81,82] atomic partial charges have been calculated at the BP86/def2-TZVPP [74-76] level of theory with GAUSSIAN 09 [79] and GENNBO 5.9 programs [83].
All energy decomposition analyses were carried out using the BP86 functional in combination with uncontracted Slater-type orbitals (STOs) as basis function for the SCF calculations [84]. The basis sets for all elements were triple-ζ quality augmented by two sets of polarizations functions and one set of diffuse functions. Core electrons were treated by the frozen-core approximation. This level of theory is denoted as BP86/TZ2P+. We did not reoptimize the geometries but used the BP86/def2-TZVPP optimized structures, because we know from previous studies that the two basis sets give very similar geometries. An auxiliary set of s, p, d, f, and g STOs was used to fit the molecular densities and to represent the Coulomb and exchange potentials accurately in each SCF cycle [85]. Scalar relativistic effects have been incorporated by applying the zeroth-order regular approximation (ZORA) [86]. The nature of the stationary points on the potential energy surface was determined by calculating the vibrational frequencies at BP86/TZ2P+. These calculations were performed with the program package ADF.2013 [87].
The bonding situation of the donor–acceptor bonds was investigated by an energy decomposition analysis (EDA) which was developed by Morokuma [88] and by Ziegler and Rauk [89,90]. The bonding analysis focuses on the instantaneous interaction energy ∆Eint of a bond A–B between two fragments A and B in the particular electronic reference state and in the frozen geometry AB. This energy is divided into three main components (Equation 1).
The term ∆Eelstat corresponds to the classical electrostatic interaction between the unperturbed charge distributions of the prepared atoms (or fragments) and it is usually attractive. The Pauli repulsion ∆EPauli is the energy change associated with the transformation from the superposition of the unperturbed wave functions of the isolated fragments to the wave function Ψ0 = NÂ[ΨAΨB], which properly obeys the Pauli principle through explicit antisymmetrization (Â operator) and renormalization (N = constant) of the product wave function. It comprises the destabilizing interactions between electrons of the same spin on either fragment. The orbital interaction ∆Eorb accounts for charge transfer and polarization effects [91]. The ∆Eorb term can be dissected into contributions from each irreducible representation of the point group of the interacting system. Further details on the EDA method and its applications to the analysis of the chemical bond [92-94] can be found in the literature.
The EDA with natural orbitals for chemical valence (EDA-NOCV) method [95] combines charge and energy decomposition schemes to split the deformation density which is associated with the bond formation, ∆ρ, into different components of the chemical bond. The EDA-NOCV calculations provide pairwise energy contributions for each pair of interaction orbitals to the total bond energy. NOCV is defined as the eigenvector of the valence operator, , given by Equation 2 [96-98].
In the EDA-NOCV scheme the orbital interaction term, ∆Eorb, is given by Equation 3.
Where and
are diagonal Kohn–Sham matrix elements corresponding to NOCVs with the eigenvalues –νk and νk, respectively. The
terms are assigned to a particular type of bond by visual inspection of the shape of the deformation density, ∆ρk. The absolute values │νk│ of the eigenvalues of Equation 3 give the charge flow which is associated with each pairwise orbital interaction. The EDA-NOCV scheme thus provides information about the charge deformation (∆ρorb) and the associated stabilization energy (∆Eorb) of the orbital interactions in chemical bonds. For more details we refer to the literature [97,98].
Results and Discussion
The optimized geometries at the BP86/def2-TZVPP level of theory of the calculated carbenes and the most important bond lengths and angles are shown in Figure 1. Experimental values of substituted analogues are given in parentheses.
![[1860-5397-11-294-1]](/bjoc/content/figures/1860-5397-11-294-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: Optimized geometries of carbenes 1–15 at the BP86/def2-TZVPP level of theory. Bond lengths and angles are given in [Å] and [°]. Experimental values are given in parentheses: 1 (Ref. [31]); 3 (Ref. [99]); 4 (Ref. [100]); 5 (Ref. [101]); 6 (Ref. [56]); 7 (Ref. [102]); 8 (Ref. [46]); 10 (Ref. [47]); 11 (Ref. [103]).
Figure 1: Optimized geometries of carbenes 1–15 at the BP86/def2-TZVPP level of theory. Bond lengths and angl...
The theoretically predicted structures are in good agreement with experimental data [31,46,47,56,99-103]. In general the computed bond lengths are slightly longer than the experimental ones. The X–Ccarb–X (X = N, C, O and S) angle in the five-membered rings slightly varies between 99.6° (10) and 105.6° (15) and is slightly larger (120.1°) in the acyclic carbene 5. This angle is often associated with the σ-donor properties which are related to the spx hybridization of the carbene lone pair orbital [2]. A first hint of the strength of the π-donation is given by the Ccarb–N bond lengths. The shortest Ccarb–N bond of 1.311 Å is calculated for the cAAC species 6, which is close to a standard C=N double bond (1.30 Å), while the longest value of 1.411 Å is calculated for the abnormal carbene 8, which approaches a standard C–N single bond (1.46 Å) [104]. The Ccarb–N bond lengths exhibit otherwise a remarkable small range between 1.35–1.38 Å. The C–N bond is slightly longer in the conjugated 6π-electron carbenes which possess some aromatic character than in the non-aromatic analogues which previously ascribed to stronger π-conjugation [105-107]. The introduction of the heteroatoms O and S in compounds 11 and 12 changes the C–N bond only slightly. The Ccarb–C bond lengths in the conjugated carbenes are between 1.404 Å (9)–1.433 Å (14) while the cAAC system 6 has a much longer distance of 1.529 Å.
Figure 2 shows the shape and energy of the frontier molecular orbitals for compounds 1–15 which are relevant for the σ-donor and π-acceptor properties. The HOMO is in all cases a carbon σ-lone pair while the LUMO (LUMO + 1 for 1, 7–10) depicts a π-orbital which has the largest coefficient at the Ccarb atom that makes it suitable for π-backdonation. The LUMOs of compounds 1, and 7–10 which are not displayed in Figure 2 are also π-orbitals which have a node at the Ccarb atom. The HOMO–LUMO energy difference varies considerably between 4.58 eV (4) and 1.55 eV (15). The small HOMO–LUMO gap of the diamidocarbene 15 comes from the very low lying LUMO which has been noted before [42]. There is clearly a correlation between the HOMO–LUMO energy difference and the calculated singlet–triplet gap of the compounds which are given at the bottom of Figure 2. The largest singlet–triplet (S/T) gap is predicted for compound 1 (91.6 kcal/mol) while compound 15 possesses the lowest S/T value (27.5 kcal/mol).
![[1860-5397-11-294-2]](/bjoc/content/figures/1860-5397-11-294-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: Frontier orbitals (BP86/def2-TZVPP) and eigenvalues (in eV) of the carbenes 1–15. The isosurfaces were taken at the 0.06 isovalue. The hydrogen atoms are omitted for clarity.
Figure 2: Frontier orbitals (BP86/def2-TZVPP) and eigenvalues (in eV) of the carbenes 1–15. The isosurfaces w...
The focus of the present work lies on the π-donation from the neighboring atoms to the carbene center X(π)→Ccarb. To estimate the size of the charge donation Δq(π) we calculated the occupation of p(π) AO of the carbene atom in molecules 1–15 which is available from the NBO analysis. Table 1 gives the computed values for the atomic charges, the orbital occupation of the σ-lone pair orbital and the occupation of p(π) AO of the Ccarb atom. We also present the Wiberg Bond Orders for the Ccarb−X bonds.
Table 1: Calculated NBO partial charges q(Ccarb) of the carbene carbon atom, occupation of the lone pair orbital Ccarb(σ) and the p(π) AO at Ccarb. Wiberg Bond Orders (WBO) for the Ccarb–X (X = C, N, O and S) bonds at BP86/def2-TZVPP.
| q(Ccarb) | Ccarb(σ) | p(π) | WBO | |
|---|---|---|---|---|
| 1 | 0.04 | 1.91 | 0.69 | 1.27 |
| 2 | 0.06 | 1.88 | 0.67 | 1.29 |
| 3 | 0.09 | 1.91 | 0.64 | 1.25 |
| 4 | 0.13 | 1.86 | 0.60 | 1.32 |
| 5 | 0.12 | 1.84 | 0.62 | 1.34 |
| 6 | 0.09 | 1.87 | 0.49 | 1.56/1.00a |
| 7 | 0.05 | 1.90 | 0.67 | 1.22/1.35a |
| 8 | −0.19 | 1.88 | 0.81 | 1.14/1.60a |
| 9 | −0.39 | 1.83 | 0.81 | 1.46 |
| 10 | −0.17 | 1.88 | 0.73 | 1.44/1.26a |
| 11 | −0.23 | 1.89 | 0.73 | 1.34/1.38a |
| 12 | 0.19 | 1.91 | 0.63 | 1.33/1.13a |
| 13 | −0.16 | 1.88 | 0.74 | 1.25/1.37a |
| 14 | −0.37 | 1.85 | 0.80 | 1.36 |
| 15 | 0.19 | 1.93 | 0.51 | 1.20 |
aThe first value is for the atom on the left side of Ccarb as shown in Figure 1.
The NBO data indicate that the occupation of the p(π) AO of the Ccarb atom is between 0.81 e (8, and 9) and 0.49 e (6). The p(π) occupation at the Ccarb atom is particularly large for the carbenes which have no heteroatoms bonded to it (9, and 14) or only one heteroatom as in 8. The special role of the cAAC species 6 which exhibits particular reactivity [52-55] that has recently been utilized for the stabilization of unusual compounds [108-117] comes to the fore by the smallest value of the p(π) occupation. Carbene 6 has also the largest bond order for the Ccarb–N bond and the smallest bond order for a Ccarb–C bond. Note that the Ccarb atom carries a negative partial charge when it is bonded to one or two carbon atoms (8–11, 13, and 14).
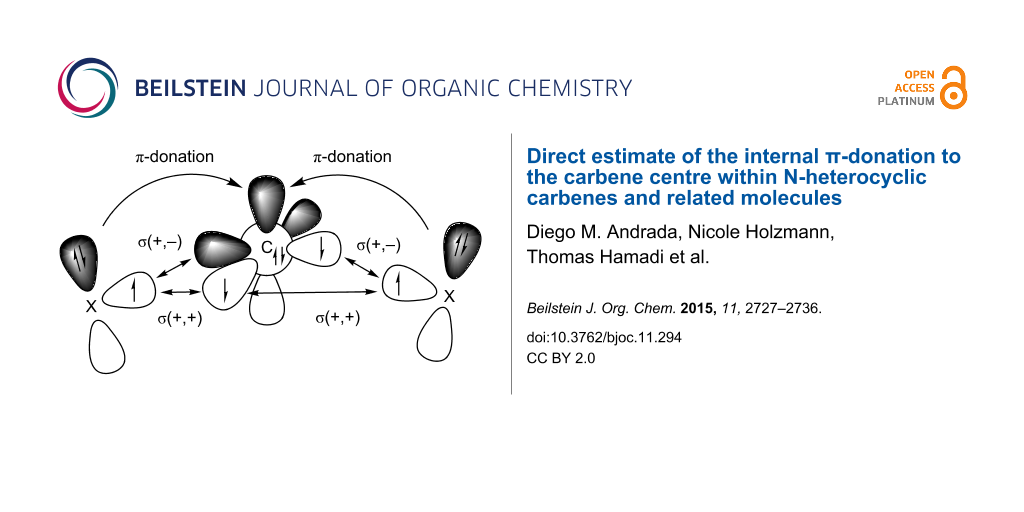
The energy contribution of the X(π)→Ccarb donation can be calculated with the EDA-NOCV method which is described in the method section. We carried out EDA-NOCV calculations using a carbon atom in the 3P ground state with the electronic configuration 2s22pσ12p||12p and the remaining fragment as interacting moieties with unpaired electrons at X. Scheme 2 shows the directly interacting atoms Ccarb and X where the electrons are placed in such a way that the unpaired electrons on both fragments are in the plane of the molecule yielding the σ-bonds while the lone pair electrons and the vacant p AO of carbon have π-symmetry with respect to the molecular plane. This leads to three major orbital interactions for σ and π-bonding between Ccarb and X. These are the σ(+,+) and σ(+,−) interactions that come from the in-phase and out-of-phase combinations of the lone-pairs, respectively, which give the two Ccarb–X σ-bonds and the π-donation X(π)→Ccarb.
Scheme 2:
Schematic view of the major orbital interactions between a carbon atom in the 3P electronic ground state with the configuration 2s22pσ12p||12p and atoms X which possess a p(π) lone pair orbital. There are σ(+,+) and σ(+,−) interactions which give the two Ccarb–X σ-bonds and the π-donation X(π)→Ccarb.
Scheme 2: Schematic view of the major orbital interactions between a carbon atom in the 3P electronic ground ...
Table 2 shows the numerical results of the EDA-NOCV calculations. The total interaction energy ΔEint between the carbon atom and the remaining fragment in the frozen geometry [118] is composed from the stabilizing orbital (covalent) interactions ΔEorb and the Coulombic term ΔEelstat and the destabilizing Pauli repulsion ΔEPauli. The strongest attraction comes from the orbital term ΔEorb. We want to point out that the trend of the intrinsic bond strength between Ccarb and the remaining fragment does not correlate with the trend of covalent bonding. The largest ΔEint values are calculated for compounds 8 and 9 but the ΔEorb values of the two species are much smaller than those of most other carbenes. The strong net bonding in 8 and 9 is rather related to the comparatively weak Pauli repulsion ΔEPauli which is much weaker than in most other species (Table 2). The interplay of all three factors ΔEorb, ΔEPauli and ΔEelstat for determining the overall net strength of chemical bonding has been highlighted before [92-94,119,120].
Table 2:
EDA-NOCV calculations at the BP86/TZ2P+ level of theory of compounds 1–15 using C(II) in the valence configuration 2s22pσ12p||1 2p and the remaining fragment as interacting moietiesa. Energy values are given in kcal/mol.
| 1 | 2 | 3 | 4b | 5b | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| ∆Eint | −322.7 | −295.2 | −309.6 | −319.5 | −314.5 | −272.3 | −302.1 | −330.85 |
| ∆EPauli | 759.2 | 825.7 | 807.5 | 804.1 | 814.41 | 734.7 | 846.2 | 669.18 |
| ∆Eelstata |
−397.8
(36.8%) |
−415.2
(37.1%) |
−413.4
(37.0%) |
−416.5
(37.1%) |
−414.6
(36.7%) |
−387.1
(38.4%) |
−426.5
(37.2%) |
−371.9
(37.2%) |
| ∆Eorba |
−684.0
(63.2%) |
−705.7
(62.9%) |
−703.7
(63.0%) |
−707.1
(62.9%) |
−714.3
(63.3%) |
−619.9
(61.6%) |
−721.7
(62.9%) |
−628.2
(62.8%) |
| ∆Eσ (+,−)c |
−319.3
(46.7%) |
−331.1
(46.9%) |
−322.1
(45.8%) |
−335.9
(47.5%) |
−353.4
(49.5%) |
−331.7
(53.5%) |
−338.7
(46.9%) |
−327.6
(52.1%) |
| ∆Eσ (+,+)c |
−233.8
(34.2%) |
−247.2
(35.0%) |
−252.2
(35.8%) |
−242.3
(34.3%) |
−223.2
(31.2%) |
−182.6
(29.5%) |
−241.7
(33.5%) |
−170.8
(27.2%) |
| ∆Eπ-donationc |
−93.4
(13.6%) |
−87.8
(12.4%) |
−89.3
(12.7%) |
−86.1
(12.2%) |
−90.2
(12.6%) |
−72.2
(11.6%) |
−92.6
(12.8%) |
−101.3
(16.1%) |
| ∆Erestc |
−37.5
(5.5%) |
−39.6
(5.6%) |
−40.1
(5.7%) |
−42.8
(6.1%) |
−47.5
(6.6%) |
−33.4
(5.4%) |
−48.7
(6.7%) |
−28.5
(4.5%) |
| 9b | 10 | 11 | 12 | 13 | 14 | 15 | ||
| ∆Eint | −336.5 | −308.9 | −263.9 | −285.9 | −312.1 | −301.6 | −280.6 | |
| ∆EPauli | 643.5 | 760.5 | 715.5 | 830.2 | 705.4 | 660.0 | 805.6 | |
| ∆Eelstata |
−377.3
(38.5%) |
−406.3
(38.0%) |
−378.1
(38.6%) |
−397.5
(35.6%) |
−380.8
(37.4%) |
−365.2
(38.0%) |
−406.6
(37.4%) |
|
| ∆Eorba |
−602.6
(61.5%) |
−663.1
(62.0%) |
−601.4
(61.4%) |
−718.5
(65.4%) |
−636.7
(62.6%) |
−596.4
(62.0%) |
−679.6
(62.6%) |
|
| ∆Eσ (+,−)c |
−285.9
(47.4%) |
−335.8
(50.6%) |
−256.9
(42.7%) |
−361.0
(50.2%) |
−326.8
(51.3%) |
−283.0
(47.5%) |
−322.0
(47.4%) |
|
| ∆Eσ (+,+)c |
−178.5
(29.6%) |
−186.6
(28.1%) |
−219.0
(36.4%) |
−235.7
(32.8%) |
−180.9
(28.4%) |
−184.9
(31.0%) |
−242.0
(35.6%) |
|
| ∆Eπ-donationc |
−109.9
(18.2%) |
−100.6
(15.2%) |
−90.0
(15.0%) |
−82.4
(11.5%) |
−96.4
(15.1%) |
−100.8
(16.9%) |
−74.0
(10.9%) |
|
| ∆Erestc |
−28.3
(4.6%) |
−40.2
(6.1%) |
−35.4 (5.9%) | −39.1 (5.4%) | −32.7 (5.1%) | −27.7 (4.6%) | −41.6 (6.1%) | |
aThe values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb. bThe symmetry Cs was enforced. cThe values in parentheses give the percentage contribution to the total orbital interactions ΔEorb.
The most important information of the EDA-NOCV calculations comes from contributions of the pairwise orbital interactions to ΔEorb. Table 2 shows that there are indeed three major terms for each molecule which can easily be identified with the schematic description that is given in Scheme 2. The deformation densities associated with the three major orbital interactions ∆Eσ (+,−), ∆Eσ (+,+) and ∆Eπ for compound 1 are shown in Figure 3. The color code of the charge deformation on bond formation is red→blue. The largest contributions comes from the formation of the Ccarb–X σ-bonds while the π-donation X(π)→Ccarb is much weaker which is reasonable. The ∆Eσ (+,−) component of the Ccarb–N σ-bond (−319.3 kcal/mol, Figure 3a) is bigger than the ∆Eσ (+,+) component (−233.8 kcal/mol, Figure 3b) which can be explained with the larger overlap of the former term (see Scheme 2). Note that the charge flows of the individual (+,+) and (+,−) interactions have different directions which cannot be easily associated to a physical meaning. It is the net charge flow which indicates the overall direction. The red and blue areas at the carbene carbon in Figure 3b indicates the polarization (change in hybridization) which takes place during the bond formation. The charge flow which is associated with the π-donation X(π)→Ccarb shows the expected direction from nitrogen to carbon. The charge flow which is associated with the three dominant orbital interactions in compound 2–15 is shown in Figure S1 of Supporting Information File 1.
![[1860-5397-11-294-3]](/bjoc/content/figures/1860-5397-11-294-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: Plot of deformation densities ∆ρ of the pairwise orbital interactions between C(3P) and N(Me)HC=CHN(Me), associated energies ∆E in kcal/mol. The color-code of the charge flow is red→blue.
Figure 3: Plot of deformation densities ∆ρ of the pairwise orbital interactions between C(3P) and N(Me)HC=CHN...
Inspection of the strength of ∆Eπ should thus reveal information about the in internal π-donation to the Ccarb atom in molecules 1–15. Table 2 suggests that the strongest X(π)→Ccarb donation is found in the 6π-conjugated carbenes 8–10, 13, and 14 where the Ccarb atom is bonded to two (9, 14) or one (8, 10, 13) carbon atoms. The weakest π-donor contributions are calculated for the cAAC species 6 and the diamidocarbene 15. It appears as if the ∆Eπ values which give the energy contribution of the X(π)→Ccarb donation which come from the EDA-NOCV calculations and the p(π) occupation which is given by the NBO method correlate. Figure 4 shows a correlation diagram between ∆Eπ and p(π). There is clearly a qualitative correlation between the two entries, but the correlation coefficient of R2 = 0.89 indicates that charge donation and associated stabilization of the different systems do not completely agree. Both methods agree that the molecules of cAAC (6) and the diamidocarbene 15 possess extremely low π-stabilization of the carbene carbon atom.
![[1860-5397-11-294-4]](/bjoc/content/figures/1860-5397-11-294-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: Plot of the ΔEπ values against NBO pπ occupation for the NHC family 1–15.
Figure 4: Plot of the ΔEπ values against NBO pπ occupation for the NHC family 1–15.
Conclusion
The NBO and EDA-NOCV calculations of the fifteen carbenes show that the carbene centre in cAAC and in diamidocarbene have the weakest X→p(π) π-donation while mesoionic carbenes possess the strongest π-donation to the carbene centre. There is a reasonable correlation between the occupation of the p(π) AO at the Ccarb atom and the energy which is associated with the X→p(π) π-donation.
Supporting Information
| Supporting Information File 1: Additional information. | ||
| Format: PDF | Size: 700.4 KB | Download |
References
-
Arduengo, A. J., III; Harlow, R. L.; Kline, M. J. Am. Chem. Soc. 1991, 113, 361. doi:10.1021/ja00001a054
Return to citation in text: [1] [2] -
Bourissou, D.; Guerret, O.; Gabbaï, F. P.; Bertrand, G. Chem. Rev. 2000, 100, 39. doi:10.1021/cr940472u
Return to citation in text: [1] [2] [3] [4] -
Schuster, O.; Yang, L.; Raubenheimer, H. G.; Albrecht, M. Chem. Rev. 2009, 109, 3445. doi:10.1021/cr8005087
Return to citation in text: [1] -
Hopkinson, M. N.; Richter, C.; Schedler, M.; Glorius, F. Nature 2014, 510, 485. doi:10.1038/nature13384
Return to citation in text: [1] -
Benhamou, L.; Chardon, E.; Lavigne, G.; Bellemin-Laponnaz, S.; César, V. Chem. Rev. 2011, 111, 2705. doi:10.1021/cr100328e
Return to citation in text: [1] -
Martin, D.; Melaimi, M.; Soleilhavoup, M.; Bertrand, G. Organometallics 2011, 30, 5304. doi:10.1021/om200650x
Return to citation in text: [1] -
Melaimi, M.; Soleilhavoup, M.; Bertrand, G. Angew. Chem., Int. Ed. 2010, 49, 8810. doi:10.1002/anie.201000165
Return to citation in text: [1] [2] -
Canac, Y.; Soleilhavoup, M.; Conejero, S.; Bertrand, G. J. Organomet. Chem. 2004, 689, 3857. doi:10.1016/j.jorganchem.2004.02.005
Return to citation in text: [1] -
Díez-González, S.; Marion, N.; Nolan, S. P. Chem. Rev. 2009, 109, 3612. doi:10.1021/cr900074m
Return to citation in text: [1] -
Levin, E.; Ivry, E.; Diesendruck, C. E.; Lemcoff, N. G. Chem. Rev. 2015, 115, 4607. doi:10.1021/cr400640e
Return to citation in text: [1] -
Schaper, L.-A.; Hock, S. J.; Herrmann, W. A.; Kühn, F. E. Angew. Chem., Int. Ed. 2013, 52, 270. doi:10.1002/anie.201205119
Return to citation in text: [1] -
Izquierdo, J.; Hutson, G. E.; Cohen, D. T.; Scheidt, K. A. Angew. Chem., Int. Ed. 2012, 51, 11686. doi:10.1002/anie.201203704
Return to citation in text: [1] -
Radius, U.; Bickelhaupt, F. M. Coord. Chem. Rev. 2009, 253, 678. doi:10.1016/j.ccr.2008.05.020
Return to citation in text: [1] -
Fèvre, M.; Pinaud, J.; Gnanou, Y.; Vignolle, J.; Taton, D. Chem. Soc. Rev. 2013, 42, 2142. doi:10.1039/c2cs35383k
Return to citation in text: [1] -
Enders, D.; Niemeier, O.; Henseler, A. Chem. Rev. 2007, 107, 5606. doi:10.1021/cr068372z
Return to citation in text: [1] -
Marion, N.; Díez-González, S.; Nolan, S. P. Angew. Chem., Int. Ed. 2007, 46, 2988. doi:10.1002/anie.200603380
Return to citation in text: [1] -
Hahn, F. E.; Jahnke, M. C. Angew. Chem., Int. Ed. 2008, 47, 3122. doi:10.1002/anie.200703883
Return to citation in text: [1] -
Zhang, D.; Zi, G. Chem. Soc. Rev. 2015, 44, 1898. doi:10.1039/C4CS00441H
Return to citation in text: [1] -
Nelson, D. J. Eur. J. Inorg. Chem. 2015, 2012. doi:10.1002/ejic.201500061
Return to citation in text: [1] -
Soleilhavoup, M.; Bertrand, G. Acc. Chem. Res. 2015, 48, 256. doi:10.1021/ar5003494
Return to citation in text: [1] [2] [3] -
Wang, Y.; Robinson, G. H. Inorg. Chem. 2014, 53, 11815. doi:10.1021/ic502231m
Return to citation in text: [1] -
Wilson, D. J. D.; Dutton, J. L. Chem. – Eur. J. 2013, 19, 13626. doi:10.1002/chem.201302715
Return to citation in text: [1] -
Wang, Y.; Robinson, G. H. Dalton Trans. 2012, 41, 337. doi:10.1039/C1DT11165E
Return to citation in text: [1] -
Wang, Y.; Robinson, G. H. Inorg. Chem. 2011, 50, 12326. doi:10.1021/ic200675u
Return to citation in text: [1] -
Rivard, E. Dalton Trans. 2014, 43, 8577. doi:10.1039/c4dt00481g
Return to citation in text: [1] -
Martin, C. D.; Soleilhavoup, M.; Bertrand, G. Chem. Sci. 2013, 4, 3020. doi:10.1039/c3sc51174j
Return to citation in text: [1] -
Martin, D.; Soleilhavoup, M.; Bertrand, G. Chem. Sci. 2011, 2, 389. doi:10.1039/C0SC00388C
Return to citation in text: [1] [2] -
Power, P. P. Nature 2010, 463, 171. doi:10.1038/nature08634
Return to citation in text: [1] -
de Frémont, P.; Marion, N.; Nolan, S. P. Coord. Chem. Rev. 2009, 253, 862. doi:10.1016/j.ccr.2008.05.018
Return to citation in text: [1] -
Regitz, M. Angew. Chem., Int. Ed. Engl. 1991, 30, 674. doi:10.1002/anie.199106741
Return to citation in text: [1] -
Arduengo, A. J., III; Rasika Dias, H. V.; Harlow, R. L.; Kline, M. J. Am. Chem. Soc. 1992, 114, 5530. doi:10.1021/ja00040a007
Return to citation in text: [1] [2] [3] -
Arduengo, A. J., III. Acc. Chem. Res. 1999, 32, 913. doi:10.1021/ar980126p
Return to citation in text: [1] -
Herrmann, W. A. Angew. Chem., Int. Ed. 2002, 41, 1290. doi:10.1002/1521-3773(20020415)41:8<1290::AID-ANIE1290>3.0.CO;2-Y
Return to citation in text: [1] -
Jacobsen, H.; Correa, A.; Poater, A.; Costabile, C.; Cavallo, L. Coord. Chem. Rev. 2009, 253, 687. doi:10.1016/j.ccr.2008.06.006
Return to citation in text: [1] [2] -
Jacobsen, H.; Correa, A.; Costabile, C.; Cavallo, L. J. Organomet. Chem. 2006, 691, 4350. doi:10.1016/j.jorganchem.2006.01.026
Return to citation in text: [1] [2] -
Nemcsok, D.; Wichmann, K.; Frenking, G. Organometallics 2004, 23, 3640. doi:10.1021/om049802j
Return to citation in text: [1] [2] -
Tonner, R.; Heydenrych, G.; Frenking, G. Chem. – Asian J. 2007, 2, 1555. doi:10.1002/asia.200700235
Return to citation in text: [1] -
Hahn, F. E.; Zabula, A. V.; Pape, T.; Hepp, A.; Tonner, R.; Haunschild, R.; Frenking, G. Chem. – Eur. J. 2008, 14, 10716. doi:10.1002/chem.200801128
Return to citation in text: [1] -
Scarborough, C. C.; Grady, M. J. W.; Guzei, I. A.; Gandhi, B. A.; Bunel, E. E.; Stahl, S. S. Angew. Chem., Int. Ed. 2005, 44, 5269. doi:10.1002/anie.200501522
Return to citation in text: [1] -
Iglesias, M.; Beetstra, D. J.; Kariuki, B.; Cavell, K. J.; Dervisi, A.; Fallis, I. A. Eur. J. Inorg. Chem. 2009, 1913. doi:10.1002/ejic.200801179
Return to citation in text: [1] -
Lu, W. Y.; Cavell, K. J.; Wixey, J. S.; Kariuki, B. Organometallics 2011, 30, 5649. doi:10.1021/om200467x
Return to citation in text: [1] -
Martin, D.; Lassauque, N.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2012, 51, 6172. doi:10.1002/anie.201202137
Return to citation in text: [1] [2] -
Martin, D.; Lassauque, N.; Steinmann, F.; Manuel, G.; Bertrand, G. Chem. – Eur. J. 2013, 19, 14895. doi:10.1002/chem.201302474
Return to citation in text: [1] -
Lavallo, V.; Dyker, C. A.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2008, 47, 5411. doi:10.1002/anie.200801176
Return to citation in text: [1] -
Fernández, I.; Dyker, C. A.; DeHope, A.; Donnadieu, B.; Frenking, G.; Bertrand, G. J. Am. Chem. Soc. 2009, 131, 11875. doi:10.1021/ja903396e
Return to citation in text: [1] -
Aldeco-Perez, E.; Rosenthal, A. J.; Donnadieu, B.; Parameswaran, P.; Frenking, G.; Bertrand, G. Science 2009, 326, 556. doi:10.1126/science.1178206
Return to citation in text: [1] [2] [3] -
Guisado-Barrios, G.; Bouffard, J.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2010, 49, 4759. doi:10.1002/anie.201001864
Return to citation in text: [1] [2] [3] -
Borthakur, B.; Phukan, A. K. Chem. – Eur. J. 2015, 21, 11603–11609. doi:10.1002/chem.201500860
Return to citation in text: [1] -
Nakafuji, S.-y.; Kobayashi, J.; Kawashima, T. Angew. Chem., Int. Ed. 2008, 47, 1141. doi:10.1002/anie.200704746
Return to citation in text: [1] -
Asay, M.; Donnadieu, B.; Baceiredo, A.; Soleilhavoup, M.; Bertrand, G. Inorg. Chem. 2008, 47, 3949. doi:10.1021/ic800459p
Return to citation in text: [1] -
Fürstner, A.; Alcarazo, M.; Radkowski, K.; Lehmann, C. W. Angew. Chem., Int. Ed. 2008, 47, 8302. doi:10.1002/anie.200803200
Return to citation in text: [1] -
Hudnall, T. W.; Bielawski, C. W. J. Am. Chem. Soc. 2009, 131, 16039. doi:10.1021/ja907481w
Return to citation in text: [1] [2] -
Hudnall, T. W.; Tennyson, A. G.; Bielawski, C. W. Organometallics 2010, 29, 4569. doi:10.1021/om1007665
Return to citation in text: [1] [2] -
César, V.; Lugan, N.; Lavigne, G. Chem. – Eur. J. 2010, 16, 11432. doi:10.1002/chem.201000870
Return to citation in text: [1] [2] -
Braun, M.; Frank, W.; Reiss, G. J.; Ganter, C. Organometallics 2010, 29, 4418. doi:10.1021/om100728n
Return to citation in text: [1] [2] -
Lavallo, V.; Canac, Y.; Präsang, C.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2005, 44, 5705. doi:10.1002/anie.200501841
Return to citation in text: [1] [2] [3] [4] -
Jazzar, R.; Dewhurst, R. D.; Bourg, J.-B.; Donnadieu, B.; Canac, Y.; Bertrand, G. Angew. Chem., Int. Ed. 2007, 46, 2899. doi:10.1002/anie.200605083
Return to citation in text: [1] [2] -
Díez-González, S.; Nolan, S. P. Coord. Chem. Rev. 2007, 251, 874. doi:10.1016/j.ccr.2006.10.004
Return to citation in text: [1] -
Curran, D. P.; Solovyev, A.; Makhlouf Brahmi, M.; Fensterbank, L.; Malacria, M.; Lacôte, E. Angew. Chem., Int. Ed. 2011, 50, 10294. doi:10.1002/anie.201102717
Return to citation in text: [1] -
Frenking, G.; Tonner, R.; Klein, S.; Takagi, N.; Shimizu, T.; Krapp, A.; Pandey, K. K.; Parameswaran, P. Chem. Soc. Rev. 2014, 43, 5106. doi:10.1039/C4CS00073K
Return to citation in text: [1] -
Dröge, T.; Glorius, F. Angew. Chem., Int. Ed. 2010, 49, 6940. doi:10.1002/anie.201001865
Return to citation in text: [1] -
Nelson, D. J.; Nolan, S. P. Chem. Soc. Rev. 2013, 42, 6723. doi:10.1039/c3cs60146c
Return to citation in text: [1] -
Fantasia, S.; Petersen, J. L.; Jacobsen, H.; Cavallo, L.; Nolan, S. P. Organometallics 2007, 26, 5880. doi:10.1021/om700857j
Return to citation in text: [1] -
Back, O.; Henry-Ellinger, M.; Martin, C. D.; Martin, D.; Bertrand, G. Angew. Chem., Int. Ed. 2013, 52, 2939. doi:10.1002/anie.201209109
Return to citation in text: [1] -
Liske, A.; Verlinden, K.; Buhl, H.; Schaper, K.; Ganter, C. Organometallics 2013, 32, 5269. doi:10.1021/om400858y
Return to citation in text: [1] -
Vummaleti, S. V. C.; Nelson, D. J.; Poater, A.; Gómez-Suárez, A.; Cordes, D. B.; Slawin, A. M. Z.; Nolan, S. P.; Cavallo, L. Chem. Sci. 2015, 6, 1895. doi:10.1039/C4SC03264K
Return to citation in text: [1] -
Alcarazo, M.; Stork, T.; Anoop, A.; Thiel, W.; Fürstner, A. Angew. Chem., Int. Ed. 2010, 49, 2542. doi:10.1002/anie.200907194
Return to citation in text: [1] -
Tukov, A. A.; Normand, A. T.; Nechaev, M. S. Dalton Trans. 2009, 7015. doi:10.1039/b906969k
Return to citation in text: [1] -
Bernhammer, J. C.; Frison, G.; Huynh, H. V. Chem. – Eur. J. 2013, 19, 12892. doi:10.1002/chem.201301093
Return to citation in text: [1] -
Huynh, H. V.; Frison, G. J. Org. Chem. 2013, 78, 328. doi:10.1021/jo302080c
Return to citation in text: [1] -
Comas-Vives, A.; Harvey, J. N. Eur. J. Inorg. Chem. 2011, 5025. doi:10.1002/ejic.201100721
Return to citation in text: [1] -
Rezabal, E.; Frison, G. J. Comput. Chem. 2015, 36, 564. doi:10.1002/jcc.23852
Return to citation in text: [1] -
Crabtree, R. H. Coord. Chem. Rev. 2013, 257, 755. doi:10.1016/j.ccr.2012.09.006
Return to citation in text: [1] -
Becke, A. D. Phys. Rev. A 1988, 38, 3098. doi:10.1103/PhysRevA.38.3098
Return to citation in text: [1] [2] -
Perdew, J. P. Phys. Rev. B 1986, 33, 8822. doi:10.1103/PhysRevB.33.8822
Return to citation in text: [1] [2] -
Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys. 2005, 7, 3297. doi:10.1039/b508541a
Return to citation in text: [1] [2] -
Peng, C.; Ayala, P. Y.; Schlegel, H. B.; Frisch, M. J. J. Comput. Chem. 1996, 17, 49. doi:10.1002/(SICI)1096-987X(19960115)17:1<49::AID-JCC5>3.0.CO;2-0
Return to citation in text: [1] -
McIver, J. W., Jr.; Komornicki, A. J. Am. Chem. Soc. 1972, 94, 2625. doi:10.1021/ja00763a011
Return to citation in text: [1] -
Gaussian 09, Revision C.01; Gaussian, Inc.: Wallingford, CT, 2009.
Return to citation in text: [1] [2] -
Wiberg, K. B. Tetrahedron 1968, 24, 1083. doi:10.1016/0040-4020(68)88057-3
Return to citation in text: [1] -
Reed, A. E.; Weinstock, R. B.; Weinhold, F. J. Chem. Phys. 1985, 83, 735. doi:10.1063/1.449486
Return to citation in text: [1] -
Reed, A. E.; Curtiss, L. A.; Weinhold, F. Chem. Rev. 1988, 88, 899. doi:10.1021/cr00088a005
Return to citation in text: [1] -
GENNBO, 5.9; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, 2009.
Return to citation in text: [1] -
Van Lenthe, E.; Baerends, E. J. J. Comput. Chem. 2003, 24, 1142. doi:10.1002/jcc.10255
Return to citation in text: [1] -
Krijn, J.; Baerends, E. J. Fit Functions in the HFS-Method; 1984.
Return to citation in text: [1] -
Van Lenthe, E.; Baerends, E. J.; Snijders, J. G. J. Chem. Phys. 1993, 99, 4597. doi:10.1063/1.466059
Return to citation in text: [1] -
te Velde, G.; Bickelhaupt, F. M.; Baerends, E. J.; Fonseca Guerra, C.; van Gisbergen, S. J. A.; Snijders, J. G.; Ziegler, T. J. Comput. Chem. 2001, 22, 931. doi:10.1002/jcc.1056
Return to citation in text: [1] -
Morokuma, K. J. Chem. Phys. 1971, 55, 1236. doi:10.1063/1.1676210
Return to citation in text: [1] -
Ziegler, T.; Rauk, A. Inorg. Chem. 1979, 18, 1755. doi:10.1021/ic50197a006
Return to citation in text: [1] -
Ziegler, T.; Rauk, A. Inorg. Chem. 1979, 18, 1558. doi:10.1021/ic50196a034
Return to citation in text: [1] -
Bickelhaupt, F. M.; Nibbering, N. M. M.; Van Wezenbeek, E. M.; Baerends, E. J. J. Phys. Chem. 1992, 96, 4864. doi:10.1021/j100191a027
Return to citation in text: [1] -
Frenking, G.; Wichmann, K.; Fröhlich, N.; Loschen, C.; Lein, M.; Frunzke, J.; Rayón, V. M. Coord. Chem. Rev. 2003, 238–239, 55. doi:10.1016/S0010-8545(02)00285-0
Return to citation in text: [1] [2] -
Krapp, A.; Bickelhaupt, F. M.; Frenking, G. Chem. – Eur. J. 2006, 12, 9196. doi:10.1002/chem.200600564
Return to citation in text: [1] [2] -
Kovács, A.; Esterhuysen, C.; Frenking, G. Chem. – Eur. J. 2005, 11, 1813. doi:10.1002/chem.200400525
Return to citation in text: [1] [2] -
Mitoraj, M. P.; Michalak, A.; Ziegler, T. J. Chem. Theory Comput. 2009, 5, 962. doi:10.1021/ct800503d
Return to citation in text: [1] -
Mitoraj, M.; Michalak, A. Organometallics 2007, 26, 6576. doi:10.1021/om700754n
Return to citation in text: [1] -
Michalak, A.; Mitoraj, M.; Ziegler, T. J. Phys. Chem. A 2008, 112, 1933. doi:10.1021/jp075460u
Return to citation in text: [1] [2] -
Mitoraj, M.; Michalak, A. J. Mol. Model. 2008, 14, 681. doi:10.1007/s00894-008-0276-1
Return to citation in text: [1] [2] -
Hahn, F. E.; Wittenbecher, L.; Boese, R.; Bläser, D. Chem. – Eur. J. 1999, 5, 1931. doi:10.1002/(SICI)1521-3765(19990604)5:6<1931::AID-CHEM1931>3.0.CO;2-M
Return to citation in text: [1] [2] -
Arduengo, A. J., III; Goerlich, J. R.; Marshall, W. J. J. Am. Chem. Soc. 1995, 117, 11027. doi:10.1021/ja00149a034
Return to citation in text: [1] [2] -
Alder, R. W.; Allen, P. R.; Murray, M.; Orpen, A. G. Angew. Chem., Int. Ed. Engl. 1996, 35, 1121. doi:10.1002/anie.199611211
Return to citation in text: [1] [2] -
Korotkikh, N. I.; Rayenko, G. F.; Shvaika, O. P.; Pekhtereva, T. M.; Cowley, A. H.; Jones, J. N.; Macdonald, C. L. B. J. Org. Chem. 2003, 68, 5762. doi:10.1021/jo034234n
Return to citation in text: [1] [2] -
Arduengo, A. J., III; Goerlich, J. R.; Marshall, W. J. Liebigs Ann./Recl. 1997, 365. doi:10.1002/jlac.199719970213
Return to citation in text: [1] [2] -
Pyykkö, P.; Atsumi, M. Chem. – Eur. J. 2009, 15, 186. doi:10.1002/chem.200800987
Return to citation in text: [1] -
Heinemann, C.; Müller, T.; Apeloig, Y.; Schwarz, H. J. Am. Chem. Soc. 1996, 118, 2023. doi:10.1021/ja9523294
Return to citation in text: [1] -
Tuononen, H. M.; Roesler, R.; Dutton, J. L.; Ragogna, P. J. Inorg. Chem. 2007, 46, 10693. doi:10.1021/ic701350e
Return to citation in text: [1] -
Boehme, C.; Frenking, G. J. Am. Chem. Soc. 1996, 118, 2039. doi:10.1021/ja9527075
Return to citation in text: [1] -
Mondal, K. C.; Roesky, H. W.; Schwarzer, M. C.; Frenking, G.; Niepötter, B.; Wolf, H.; Herbst-Irmer, R.; Stalke, D. Angew. Chem., Int. Ed. 2013, 52, 2963. doi:10.1002/anie.201208307
Return to citation in text: [1] -
Mondal, K. C.; Roesky, H. W.; Schwarzer, M. C.; Frenking, G.; Tkach, I.; Wolf, H.; Kratzert, D.; Herbst-Irmer, R.; Niepötter, B.; Stalke, D. Angew. Chem., Int. Ed. 2013, 52, 1801. doi:10.1002/anie.201204487
Return to citation in text: [1] -
Singh, A. P.; Samuel, P. P.; Roesky, H. W.; Schwarzer, M. C.; Frenking, G.; Sidhu, N. S.; Dittrich, B. J. Am. Chem. Soc. 2013, 135, 7324. doi:10.1021/ja402351x
Return to citation in text: [1] -
Weinberger, D. S.; Melaimi, M.; Moore, C. E.; Rheingold, A. L.; Frenking, G.; Jerabek, P.; Bertrand, G. Angew. Chem., Int. Ed. 2013, 52, 8964. doi:10.1002/anie.201304820
Return to citation in text: [1] -
Samuel, P. P.; Mondal, K. C.; Roesky, H. W.; Hermann, M.; Frenking, G.; Demeshko, S.; Meyer, F.; Stückl, A. C.; Christian, J. H.; Dalal, N. S.; Ungur, L.; Chibotaru, L. F.; Pröpper, K.; Meents, A.; Dittrich, B. Angew. Chem., Int. Ed. 2013, 52, 11817. doi:10.1002/anie.201304642
Return to citation in text: [1] -
Mondal, K. C.; Samuel, P. P.; Roesky, H. W.; Carl, E.; Herbst-Irmer, R.; Stalke, D.; Schwederski, B.; Kaim, W.; Ungur, L.; Chibotaru, L. F.; Hermann, M.; Frenking, G. J. Am. Chem. Soc. 2014, 136, 1770. doi:10.1021/ja4123285
Return to citation in text: [1] -
Weinberger, D. S.; Amin Sk, N.; Mondal, K. C.; Melaimi, M.; Bertrand, G.; Stückl, A. C.; Roesky, H. W.; Dittrich, B.; Demeshko, S.; Schwederski, B.; Kaim, W.; Jerabek, P.; Frenking, G. J. Am. Chem. Soc. 2014, 136, 6235. doi:10.1021/ja502521b
Return to citation in text: [1] -
Mondal, K. C.; Samuel, P. P.; Roesky, H. W.; Aysin, R. R.; Leites, L. A.; Neudeck, S.; Lübben, J.; Dittrich, B.; Holzmann, N.; Hermann, M.; Frenking, G. J. Am. Chem. Soc. 2014, 136, 8919. doi:10.1021/ja504821u
Return to citation in text: [1] -
Roy, S.; Mondal, K. C.; Meyer, J.; Niepötter, B.; Köhler, C.; Herbst-Irmer, R.; Stalke, D.; Dittrich, B.; Andrada, D. M.; Frenking, G.; Roesky, H. W. Chem. – Eur. J. 2015, 21, 9312. doi:10.1002/chem.201500758
Return to citation in text: [1] -
Roy, S.; Stollberg, P.; Herbst-Irmer, R.; Stalke, D.; Andrada, D. M.; Frenking, G.; Roesky, H. W. J. Am. Chem. Soc. 2015, 137, 150. doi:10.1021/ja512089e
Return to citation in text: [1] -
The molecules 4, 5 and 9 were calculated for technical reasons with enforce Cs symmetry in order to align the single occupied orbitals in the right way. The energy differences to the fully optimized structures are negligible and thus, the results for the structures with Cs symmetry can be used for the bonding analysis of the equilibrium structures.
Return to citation in text: [1] -
Esterhuysen, C.; Frenking, G. Theor. Chem. Acc. 2004, 111, 381. doi:10.1007/s00214-003-0535-2
Return to citation in text: [1] -
Frenking, G.; Wichmann, K.; Fröhlich, N.; Grobe, J.; Golla, W.; Le Van, D.; Krebs, B.; Läge, M. Organometallics 2002, 21, 2921. doi:10.1021/om020311d
Return to citation in text: [1]
| 74. | Becke, A. D. Phys. Rev. A 1988, 38, 3098. doi:10.1103/PhysRevA.38.3098 |
| 75. | Perdew, J. P. Phys. Rev. B 1986, 33, 8822. doi:10.1103/PhysRevB.33.8822 |
| 76. | Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys. 2005, 7, 3297. doi:10.1039/b508541a |
| 77. | Peng, C.; Ayala, P. Y.; Schlegel, H. B.; Frisch, M. J. J. Comput. Chem. 1996, 17, 49. doi:10.1002/(SICI)1096-987X(19960115)17:1<49::AID-JCC5>3.0.CO;2-0 |
| 83. | GENNBO, 5.9; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, 2009. |
| 84. | Van Lenthe, E.; Baerends, E. J. J. Comput. Chem. 2003, 24, 1142. doi:10.1002/jcc.10255 |
| 74. | Becke, A. D. Phys. Rev. A 1988, 38, 3098. doi:10.1103/PhysRevA.38.3098 |
| 75. | Perdew, J. P. Phys. Rev. B 1986, 33, 8822. doi:10.1103/PhysRevB.33.8822 |
| 76. | Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys. 2005, 7, 3297. doi:10.1039/b508541a |
| 81. | Reed, A. E.; Weinstock, R. B.; Weinhold, F. J. Chem. Phys. 1985, 83, 735. doi:10.1063/1.449486 |
| 82. | Reed, A. E.; Curtiss, L. A.; Weinhold, F. Chem. Rev. 1988, 88, 899. doi:10.1021/cr00088a005 |
| 78. | McIver, J. W., Jr.; Komornicki, A. J. Am. Chem. Soc. 1972, 94, 2625. doi:10.1021/ja00763a011 |
| 86. | Van Lenthe, E.; Baerends, E. J.; Snijders, J. G. J. Chem. Phys. 1993, 99, 4597. doi:10.1063/1.466059 |
| 87. | te Velde, G.; Bickelhaupt, F. M.; Baerends, E. J.; Fonseca Guerra, C.; van Gisbergen, S. J. A.; Snijders, J. G.; Ziegler, T. J. Comput. Chem. 2001, 22, 931. doi:10.1002/jcc.1056 |
| 97. | Michalak, A.; Mitoraj, M.; Ziegler, T. J. Phys. Chem. A 2008, 112, 1933. doi:10.1021/jp075460u |
| 98. | Mitoraj, M.; Michalak, A. J. Mol. Model. 2008, 14, 681. doi:10.1007/s00894-008-0276-1 |
| 31. | Arduengo, A. J., III; Rasika Dias, H. V.; Harlow, R. L.; Kline, M. J. Am. Chem. Soc. 1992, 114, 5530. doi:10.1021/ja00040a007 |
| 95. | Mitoraj, M. P.; Michalak, A.; Ziegler, T. J. Chem. Theory Comput. 2009, 5, 962. doi:10.1021/ct800503d |
| 96. | Mitoraj, M.; Michalak, A. Organometallics 2007, 26, 6576. doi:10.1021/om700754n |
| 97. | Michalak, A.; Mitoraj, M.; Ziegler, T. J. Phys. Chem. A 2008, 112, 1933. doi:10.1021/jp075460u |
| 98. | Mitoraj, M.; Michalak, A. J. Mol. Model. 2008, 14, 681. doi:10.1007/s00894-008-0276-1 |
| 91. | Bickelhaupt, F. M.; Nibbering, N. M. M.; Van Wezenbeek, E. M.; Baerends, E. J. J. Phys. Chem. 1992, 96, 4864. doi:10.1021/j100191a027 |
| 92. | Frenking, G.; Wichmann, K.; Fröhlich, N.; Loschen, C.; Lein, M.; Frunzke, J.; Rayón, V. M. Coord. Chem. Rev. 2003, 238–239, 55. doi:10.1016/S0010-8545(02)00285-0 |
| 93. | Krapp, A.; Bickelhaupt, F. M.; Frenking, G. Chem. – Eur. J. 2006, 12, 9196. doi:10.1002/chem.200600564 |
| 94. | Kovács, A.; Esterhuysen, C.; Frenking, G. Chem. – Eur. J. 2005, 11, 1813. doi:10.1002/chem.200400525 |
| 89. | Ziegler, T.; Rauk, A. Inorg. Chem. 1979, 18, 1755. doi:10.1021/ic50197a006 |
| 90. | Ziegler, T.; Rauk, A. Inorg. Chem. 1979, 18, 1558. doi:10.1021/ic50196a034 |
| 100. | Arduengo, A. J., III; Goerlich, J. R.; Marshall, W. J. J. Am. Chem. Soc. 1995, 117, 11027. doi:10.1021/ja00149a034 |
| 101. | Alder, R. W.; Allen, P. R.; Murray, M.; Orpen, A. G. Angew. Chem., Int. Ed. Engl. 1996, 35, 1121. doi:10.1002/anie.199611211 |
| 99. | Hahn, F. E.; Wittenbecher, L.; Boese, R.; Bläser, D. Chem. – Eur. J. 1999, 5, 1931. doi:10.1002/(SICI)1521-3765(19990604)5:6<1931::AID-CHEM1931>3.0.CO;2-M |
| 1. | Arduengo, A. J., III; Harlow, R. L.; Kline, M. J. Am. Chem. Soc. 1991, 113, 361. doi:10.1021/ja00001a054 |
| 14. | Fèvre, M.; Pinaud, J.; Gnanou, Y.; Vignolle, J.; Taton, D. Chem. Soc. Rev. 2013, 42, 2142. doi:10.1039/c2cs35383k |
| 15. | Enders, D.; Niemeier, O.; Henseler, A. Chem. Rev. 2007, 107, 5606. doi:10.1021/cr068372z |
| 16. | Marion, N.; Díez-González, S.; Nolan, S. P. Angew. Chem., Int. Ed. 2007, 46, 2988. doi:10.1002/anie.200603380 |
| 42. | Martin, D.; Lassauque, N.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2012, 51, 6172. doi:10.1002/anie.201202137 |
| 43. | Martin, D.; Lassauque, N.; Steinmann, F.; Manuel, G.; Bertrand, G. Chem. – Eur. J. 2013, 19, 14895. doi:10.1002/chem.201302474 |
| 2. | Bourissou, D.; Guerret, O.; Gabbaï, F. P.; Bertrand, G. Chem. Rev. 2000, 100, 39. doi:10.1021/cr940472u |
| 9. | Díez-González, S.; Marion, N.; Nolan, S. P. Chem. Rev. 2009, 109, 3612. doi:10.1021/cr900074m |
| 10. | Levin, E.; Ivry, E.; Diesendruck, C. E.; Lemcoff, N. G. Chem. Rev. 2015, 115, 4607. doi:10.1021/cr400640e |
| 11. | Schaper, L.-A.; Hock, S. J.; Herrmann, W. A.; Kühn, F. E. Angew. Chem., Int. Ed. 2013, 52, 270. doi:10.1002/anie.201205119 |
| 12. | Izquierdo, J.; Hutson, G. E.; Cohen, D. T.; Scheidt, K. A. Angew. Chem., Int. Ed. 2012, 51, 11686. doi:10.1002/anie.201203704 |
| 13. | Radius, U.; Bickelhaupt, F. M. Coord. Chem. Rev. 2009, 253, 678. doi:10.1016/j.ccr.2008.05.020 |
| 44. | Lavallo, V.; Dyker, C. A.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2008, 47, 5411. doi:10.1002/anie.200801176 |
| 45. | Fernández, I.; Dyker, C. A.; DeHope, A.; Donnadieu, B.; Frenking, G.; Bertrand, G. J. Am. Chem. Soc. 2009, 131, 11875. doi:10.1021/ja903396e |
| 46. | Aldeco-Perez, E.; Rosenthal, A. J.; Donnadieu, B.; Parameswaran, P.; Frenking, G.; Bertrand, G. Science 2009, 326, 556. doi:10.1126/science.1178206 |
| 47. | Guisado-Barrios, G.; Bouffard, J.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2010, 49, 4759. doi:10.1002/anie.201001864 |
| 5. | Benhamou, L.; Chardon, E.; Lavigne, G.; Bellemin-Laponnaz, S.; César, V. Chem. Rev. 2011, 111, 2705. doi:10.1021/cr100328e |
| 6. | Martin, D.; Melaimi, M.; Soleilhavoup, M.; Bertrand, G. Organometallics 2011, 30, 5304. doi:10.1021/om200650x |
| 7. | Melaimi, M.; Soleilhavoup, M.; Bertrand, G. Angew. Chem., Int. Ed. 2010, 49, 8810. doi:10.1002/anie.201000165 |
| 8. | Canac, Y.; Soleilhavoup, M.; Conejero, S.; Bertrand, G. J. Organomet. Chem. 2004, 689, 3857. doi:10.1016/j.jorganchem.2004.02.005 |
| 39. | Scarborough, C. C.; Grady, M. J. W.; Guzei, I. A.; Gandhi, B. A.; Bunel, E. E.; Stahl, S. S. Angew. Chem., Int. Ed. 2005, 44, 5269. doi:10.1002/anie.200501522 |
| 40. | Iglesias, M.; Beetstra, D. J.; Kariuki, B.; Cavell, K. J.; Dervisi, A.; Fallis, I. A. Eur. J. Inorg. Chem. 2009, 1913. doi:10.1002/ejic.200801179 |
| 41. | Lu, W. Y.; Cavell, K. J.; Wixey, J. S.; Kariuki, B. Organometallics 2011, 30, 5649. doi:10.1021/om200467x |
| 103. | Arduengo, A. J., III; Goerlich, J. R.; Marshall, W. J. Liebigs Ann./Recl. 1997, 365. doi:10.1002/jlac.199719970213 |
| 2. | Bourissou, D.; Guerret, O.; Gabbaï, F. P.; Bertrand, G. Chem. Rev. 2000, 100, 39. doi:10.1021/cr940472u |
| 3. | Schuster, O.; Yang, L.; Raubenheimer, H. G.; Albrecht, M. Chem. Rev. 2009, 109, 3445. doi:10.1021/cr8005087 |
| 4. | Hopkinson, M. N.; Richter, C.; Schedler, M.; Glorius, F. Nature 2014, 510, 485. doi:10.1038/nature13384 |
| 7. | Melaimi, M.; Soleilhavoup, M.; Bertrand, G. Angew. Chem., Int. Ed. 2010, 49, 8810. doi:10.1002/anie.201000165 |
| 31. | Arduengo, A. J., III; Rasika Dias, H. V.; Harlow, R. L.; Kline, M. J. Am. Chem. Soc. 1992, 114, 5530. doi:10.1021/ja00040a007 |
| 46. | Aldeco-Perez, E.; Rosenthal, A. J.; Donnadieu, B.; Parameswaran, P.; Frenking, G.; Bertrand, G. Science 2009, 326, 556. doi:10.1126/science.1178206 |
| 47. | Guisado-Barrios, G.; Bouffard, J.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2010, 49, 4759. doi:10.1002/anie.201001864 |
| 56. | Lavallo, V.; Canac, Y.; Präsang, C.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2005, 44, 5705. doi:10.1002/anie.200501841 |
| 99. | Hahn, F. E.; Wittenbecher, L.; Boese, R.; Bläser, D. Chem. – Eur. J. 1999, 5, 1931. doi:10.1002/(SICI)1521-3765(19990604)5:6<1931::AID-CHEM1931>3.0.CO;2-M |
| 100. | Arduengo, A. J., III; Goerlich, J. R.; Marshall, W. J. J. Am. Chem. Soc. 1995, 117, 11027. doi:10.1021/ja00149a034 |
| 101. | Alder, R. W.; Allen, P. R.; Murray, M.; Orpen, A. G. Angew. Chem., Int. Ed. Engl. 1996, 35, 1121. doi:10.1002/anie.199611211 |
| 102. | Korotkikh, N. I.; Rayenko, G. F.; Shvaika, O. P.; Pekhtereva, T. M.; Cowley, A. H.; Jones, J. N.; Macdonald, C. L. B. J. Org. Chem. 2003, 68, 5762. doi:10.1021/jo034234n |
| 103. | Arduengo, A. J., III; Goerlich, J. R.; Marshall, W. J. Liebigs Ann./Recl. 1997, 365. doi:10.1002/jlac.199719970213 |
| 2. | Bourissou, D.; Guerret, O.; Gabbaï, F. P.; Bertrand, G. Chem. Rev. 2000, 100, 39. doi:10.1021/cr940472u |
| 29. | de Frémont, P.; Marion, N.; Nolan, S. P. Coord. Chem. Rev. 2009, 253, 862. doi:10.1016/j.ccr.2008.05.018 |
| 32. | Arduengo, A. J., III. Acc. Chem. Res. 1999, 32, 913. doi:10.1021/ar980126p |
| 33. | Herrmann, W. A. Angew. Chem., Int. Ed. 2002, 41, 1290. doi:10.1002/1521-3773(20020415)41:8<1290::AID-ANIE1290>3.0.CO;2-Y |
| 46. | Aldeco-Perez, E.; Rosenthal, A. J.; Donnadieu, B.; Parameswaran, P.; Frenking, G.; Bertrand, G. Science 2009, 326, 556. doi:10.1126/science.1178206 |
| 27. | Martin, D.; Soleilhavoup, M.; Bertrand, G. Chem. Sci. 2011, 2, 389. doi:10.1039/C0SC00388C |
| 28. | Power, P. P. Nature 2010, 463, 171. doi:10.1038/nature08634 |
| 34. | Jacobsen, H.; Correa, A.; Poater, A.; Costabile, C.; Cavallo, L. Coord. Chem. Rev. 2009, 253, 687. doi:10.1016/j.ccr.2008.06.006 |
| 35. | Jacobsen, H.; Correa, A.; Costabile, C.; Cavallo, L. J. Organomet. Chem. 2006, 691, 4350. doi:10.1016/j.jorganchem.2006.01.026 |
| 36. | Nemcsok, D.; Wichmann, K.; Frenking, G. Organometallics 2004, 23, 3640. doi:10.1021/om049802j |
| 37. | Tonner, R.; Heydenrych, G.; Frenking, G. Chem. – Asian J. 2007, 2, 1555. doi:10.1002/asia.200700235 |
| 38. | Hahn, F. E.; Zabula, A. V.; Pape, T.; Hepp, A.; Tonner, R.; Haunschild, R.; Frenking, G. Chem. – Eur. J. 2008, 14, 10716. doi:10.1002/chem.200801128 |
| 47. | Guisado-Barrios, G.; Bouffard, J.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2010, 49, 4759. doi:10.1002/anie.201001864 |
| 20. | Soleilhavoup, M.; Bertrand, G. Acc. Chem. Res. 2015, 48, 256. doi:10.1021/ar5003494 |
| 21. | Wang, Y.; Robinson, G. H. Inorg. Chem. 2014, 53, 11815. doi:10.1021/ic502231m |
| 22. | Wilson, D. J. D.; Dutton, J. L. Chem. – Eur. J. 2013, 19, 13626. doi:10.1002/chem.201302715 |
| 23. | Wang, Y.; Robinson, G. H. Dalton Trans. 2012, 41, 337. doi:10.1039/C1DT11165E |
| 24. | Wang, Y.; Robinson, G. H. Inorg. Chem. 2011, 50, 12326. doi:10.1021/ic200675u |
| 25. | Rivard, E. Dalton Trans. 2014, 43, 8577. doi:10.1039/c4dt00481g |
| 26. | Martin, C. D.; Soleilhavoup, M.; Bertrand, G. Chem. Sci. 2013, 4, 3020. doi:10.1039/c3sc51174j |
| 56. | Lavallo, V.; Canac, Y.; Präsang, C.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2005, 44, 5705. doi:10.1002/anie.200501841 |
| 17. | Hahn, F. E.; Jahnke, M. C. Angew. Chem., Int. Ed. 2008, 47, 3122. doi:10.1002/anie.200703883 |
| 18. | Zhang, D.; Zi, G. Chem. Soc. Rev. 2015, 44, 1898. doi:10.1039/C4CS00441H |
| 19. | Nelson, D. J. Eur. J. Inorg. Chem. 2015, 2012. doi:10.1002/ejic.201500061 |
| 1. | Arduengo, A. J., III; Harlow, R. L.; Kline, M. J. Am. Chem. Soc. 1991, 113, 361. doi:10.1021/ja00001a054 |
| 2. | Bourissou, D.; Guerret, O.; Gabbaï, F. P.; Bertrand, G. Chem. Rev. 2000, 100, 39. doi:10.1021/cr940472u |
| 30. | Regitz, M. Angew. Chem., Int. Ed. Engl. 1991, 30, 674. doi:10.1002/anie.199106741 |
| 31. | Arduengo, A. J., III; Rasika Dias, H. V.; Harlow, R. L.; Kline, M. J. Am. Chem. Soc. 1992, 114, 5530. doi:10.1021/ja00040a007 |
| 102. | Korotkikh, N. I.; Rayenko, G. F.; Shvaika, O. P.; Pekhtereva, T. M.; Cowley, A. H.; Jones, J. N.; Macdonald, C. L. B. J. Org. Chem. 2003, 68, 5762. doi:10.1021/jo034234n |
| 20. | Soleilhavoup, M.; Bertrand, G. Acc. Chem. Res. 2015, 48, 256. doi:10.1021/ar5003494 |
| 56. | Lavallo, V.; Canac, Y.; Präsang, C.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2005, 44, 5705. doi:10.1002/anie.200501841 |
| 57. | Jazzar, R.; Dewhurst, R. D.; Bourg, J.-B.; Donnadieu, B.; Canac, Y.; Bertrand, G. Angew. Chem., Int. Ed. 2007, 46, 2899. doi:10.1002/anie.200605083 |
| 48. | Borthakur, B.; Phukan, A. K. Chem. – Eur. J. 2015, 21, 11603–11609. doi:10.1002/chem.201500860 |
| 49. | Nakafuji, S.-y.; Kobayashi, J.; Kawashima, T. Angew. Chem., Int. Ed. 2008, 47, 1141. doi:10.1002/anie.200704746 |
| 50. | Asay, M.; Donnadieu, B.; Baceiredo, A.; Soleilhavoup, M.; Bertrand, G. Inorg. Chem. 2008, 47, 3949. doi:10.1021/ic800459p |
| 51. | Fürstner, A.; Alcarazo, M.; Radkowski, K.; Lehmann, C. W. Angew. Chem., Int. Ed. 2008, 47, 8302. doi:10.1002/anie.200803200 |
| 52. | Hudnall, T. W.; Bielawski, C. W. J. Am. Chem. Soc. 2009, 131, 16039. doi:10.1021/ja907481w |
| 53. | Hudnall, T. W.; Tennyson, A. G.; Bielawski, C. W. Organometallics 2010, 29, 4569. doi:10.1021/om1007665 |
| 54. | César, V.; Lugan, N.; Lavigne, G. Chem. – Eur. J. 2010, 16, 11432. doi:10.1002/chem.201000870 |
| 55. | Braun, M.; Frank, W.; Reiss, G. J.; Ganter, C. Organometallics 2010, 29, 4418. doi:10.1021/om100728n |
| 42. | Martin, D.; Lassauque, N.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2012, 51, 6172. doi:10.1002/anie.201202137 |
| 52. | Hudnall, T. W.; Bielawski, C. W. J. Am. Chem. Soc. 2009, 131, 16039. doi:10.1021/ja907481w |
| 53. | Hudnall, T. W.; Tennyson, A. G.; Bielawski, C. W. Organometallics 2010, 29, 4569. doi:10.1021/om1007665 |
| 54. | César, V.; Lugan, N.; Lavigne, G. Chem. – Eur. J. 2010, 16, 11432. doi:10.1002/chem.201000870 |
| 55. | Braun, M.; Frank, W.; Reiss, G. J.; Ganter, C. Organometallics 2010, 29, 4418. doi:10.1021/om100728n |
| 104. | Pyykkö, P.; Atsumi, M. Chem. – Eur. J. 2009, 15, 186. doi:10.1002/chem.200800987 |
| 105. | Heinemann, C.; Müller, T.; Apeloig, Y.; Schwarz, H. J. Am. Chem. Soc. 1996, 118, 2023. doi:10.1021/ja9523294 |
| 106. | Tuononen, H. M.; Roesler, R.; Dutton, J. L.; Ragogna, P. J. Inorg. Chem. 2007, 46, 10693. doi:10.1021/ic701350e |
| 107. | Boehme, C.; Frenking, G. J. Am. Chem. Soc. 1996, 118, 2039. doi:10.1021/ja9527075 |
| 35. | Jacobsen, H.; Correa, A.; Costabile, C.; Cavallo, L. J. Organomet. Chem. 2006, 691, 4350. doi:10.1016/j.jorganchem.2006.01.026 |
| 67. | Alcarazo, M.; Stork, T.; Anoop, A.; Thiel, W.; Fürstner, A. Angew. Chem., Int. Ed. 2010, 49, 2542. doi:10.1002/anie.200907194 |
| 68. | Tukov, A. A.; Normand, A. T.; Nechaev, M. S. Dalton Trans. 2009, 7015. doi:10.1039/b906969k |
| 69. | Bernhammer, J. C.; Frison, G.; Huynh, H. V. Chem. – Eur. J. 2013, 19, 12892. doi:10.1002/chem.201301093 |
| 70. | Huynh, H. V.; Frison, G. J. Org. Chem. 2013, 78, 328. doi:10.1021/jo302080c |
| 71. | Comas-Vives, A.; Harvey, J. N. Eur. J. Inorg. Chem. 2011, 5025. doi:10.1002/ejic.201100721 |
| 72. | Rezabal, E.; Frison, G. J. Comput. Chem. 2015, 36, 564. doi:10.1002/jcc.23852 |
| 73. | Crabtree, R. H. Coord. Chem. Rev. 2013, 257, 755. doi:10.1016/j.ccr.2012.09.006 |
| 64. | Back, O.; Henry-Ellinger, M.; Martin, C. D.; Martin, D.; Bertrand, G. Angew. Chem., Int. Ed. 2013, 52, 2939. doi:10.1002/anie.201209109 |
| 65. | Liske, A.; Verlinden, K.; Buhl, H.; Schaper, K.; Ganter, C. Organometallics 2013, 32, 5269. doi:10.1021/om400858y |
| 66. | Vummaleti, S. V. C.; Nelson, D. J.; Poater, A.; Gómez-Suárez, A.; Cordes, D. B.; Slawin, A. M. Z.; Nolan, S. P.; Cavallo, L. Chem. Sci. 2015, 6, 1895. doi:10.1039/C4SC03264K |
| 61. | Dröge, T.; Glorius, F. Angew. Chem., Int. Ed. 2010, 49, 6940. doi:10.1002/anie.201001865 |
| 62. | Nelson, D. J.; Nolan, S. P. Chem. Soc. Rev. 2013, 42, 6723. doi:10.1039/c3cs60146c |
| 92. | Frenking, G.; Wichmann, K.; Fröhlich, N.; Loschen, C.; Lein, M.; Frunzke, J.; Rayón, V. M. Coord. Chem. Rev. 2003, 238–239, 55. doi:10.1016/S0010-8545(02)00285-0 |
| 93. | Krapp, A.; Bickelhaupt, F. M.; Frenking, G. Chem. – Eur. J. 2006, 12, 9196. doi:10.1002/chem.200600564 |
| 94. | Kovács, A.; Esterhuysen, C.; Frenking, G. Chem. – Eur. J. 2005, 11, 1813. doi:10.1002/chem.200400525 |
| 119. | Esterhuysen, C.; Frenking, G. Theor. Chem. Acc. 2004, 111, 381. doi:10.1007/s00214-003-0535-2 |
| 120. | Frenking, G.; Wichmann, K.; Fröhlich, N.; Grobe, J.; Golla, W.; Le Van, D.; Krebs, B.; Läge, M. Organometallics 2002, 21, 2921. doi:10.1021/om020311d |
| 63. | Fantasia, S.; Petersen, J. L.; Jacobsen, H.; Cavallo, L.; Nolan, S. P. Organometallics 2007, 26, 5880. doi:10.1021/om700857j |
| 20. | Soleilhavoup, M.; Bertrand, G. Acc. Chem. Res. 2015, 48, 256. doi:10.1021/ar5003494 |
| 56. | Lavallo, V.; Canac, Y.; Präsang, C.; Donnadieu, B.; Bertrand, G. Angew. Chem., Int. Ed. 2005, 44, 5705. doi:10.1002/anie.200501841 |
| 57. | Jazzar, R.; Dewhurst, R. D.; Bourg, J.-B.; Donnadieu, B.; Canac, Y.; Bertrand, G. Angew. Chem., Int. Ed. 2007, 46, 2899. doi:10.1002/anie.200605083 |
| 108. | Mondal, K. C.; Roesky, H. W.; Schwarzer, M. C.; Frenking, G.; Niepötter, B.; Wolf, H.; Herbst-Irmer, R.; Stalke, D. Angew. Chem., Int. Ed. 2013, 52, 2963. doi:10.1002/anie.201208307 |
| 109. | Mondal, K. C.; Roesky, H. W.; Schwarzer, M. C.; Frenking, G.; Tkach, I.; Wolf, H.; Kratzert, D.; Herbst-Irmer, R.; Niepötter, B.; Stalke, D. Angew. Chem., Int. Ed. 2013, 52, 1801. doi:10.1002/anie.201204487 |
| 110. | Singh, A. P.; Samuel, P. P.; Roesky, H. W.; Schwarzer, M. C.; Frenking, G.; Sidhu, N. S.; Dittrich, B. J. Am. Chem. Soc. 2013, 135, 7324. doi:10.1021/ja402351x |
| 111. | Weinberger, D. S.; Melaimi, M.; Moore, C. E.; Rheingold, A. L.; Frenking, G.; Jerabek, P.; Bertrand, G. Angew. Chem., Int. Ed. 2013, 52, 8964. doi:10.1002/anie.201304820 |
| 112. | Samuel, P. P.; Mondal, K. C.; Roesky, H. W.; Hermann, M.; Frenking, G.; Demeshko, S.; Meyer, F.; Stückl, A. C.; Christian, J. H.; Dalal, N. S.; Ungur, L.; Chibotaru, L. F.; Pröpper, K.; Meents, A.; Dittrich, B. Angew. Chem., Int. Ed. 2013, 52, 11817. doi:10.1002/anie.201304642 |
| 113. | Mondal, K. C.; Samuel, P. P.; Roesky, H. W.; Carl, E.; Herbst-Irmer, R.; Stalke, D.; Schwederski, B.; Kaim, W.; Ungur, L.; Chibotaru, L. F.; Hermann, M.; Frenking, G. J. Am. Chem. Soc. 2014, 136, 1770. doi:10.1021/ja4123285 |
| 114. | Weinberger, D. S.; Amin Sk, N.; Mondal, K. C.; Melaimi, M.; Bertrand, G.; Stückl, A. C.; Roesky, H. W.; Dittrich, B.; Demeshko, S.; Schwederski, B.; Kaim, W.; Jerabek, P.; Frenking, G. J. Am. Chem. Soc. 2014, 136, 6235. doi:10.1021/ja502521b |
| 115. | Mondal, K. C.; Samuel, P. P.; Roesky, H. W.; Aysin, R. R.; Leites, L. A.; Neudeck, S.; Lübben, J.; Dittrich, B.; Holzmann, N.; Hermann, M.; Frenking, G. J. Am. Chem. Soc. 2014, 136, 8919. doi:10.1021/ja504821u |
| 116. | Roy, S.; Mondal, K. C.; Meyer, J.; Niepötter, B.; Köhler, C.; Herbst-Irmer, R.; Stalke, D.; Dittrich, B.; Andrada, D. M.; Frenking, G.; Roesky, H. W. Chem. – Eur. J. 2015, 21, 9312. doi:10.1002/chem.201500758 |
| 117. | Roy, S.; Stollberg, P.; Herbst-Irmer, R.; Stalke, D.; Andrada, D. M.; Frenking, G.; Roesky, H. W. J. Am. Chem. Soc. 2015, 137, 150. doi:10.1021/ja512089e |
| 27. | Martin, D.; Soleilhavoup, M.; Bertrand, G. Chem. Sci. 2011, 2, 389. doi:10.1039/C0SC00388C |
| 34. | Jacobsen, H.; Correa, A.; Poater, A.; Costabile, C.; Cavallo, L. Coord. Chem. Rev. 2009, 253, 687. doi:10.1016/j.ccr.2008.06.006 |
| 36. | Nemcsok, D.; Wichmann, K.; Frenking, G. Organometallics 2004, 23, 3640. doi:10.1021/om049802j |
| 58. | Díez-González, S.; Nolan, S. P. Coord. Chem. Rev. 2007, 251, 874. doi:10.1016/j.ccr.2006.10.004 |
| 59. | Curran, D. P.; Solovyev, A.; Makhlouf Brahmi, M.; Fensterbank, L.; Malacria, M.; Lacôte, E. Angew. Chem., Int. Ed. 2011, 50, 10294. doi:10.1002/anie.201102717 |
| 60. | Frenking, G.; Tonner, R.; Klein, S.; Takagi, N.; Shimizu, T.; Krapp, A.; Pandey, K. K.; Parameswaran, P. Chem. Soc. Rev. 2014, 43, 5106. doi:10.1039/C4CS00073K |
| 118. | The molecules 4, 5 and 9 were calculated for technical reasons with enforce Cs symmetry in order to align the single occupied orbitals in the right way. The energy differences to the fully optimized structures are negligible and thus, the results for the structures with Cs symmetry can be used for the bonding analysis of the equilibrium structures. |
© 2015 Andrada et al; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Organic Chemistry terms and conditions: (http://www.beilstein-journals.org/bjoc)