Abstract
We report a combined experimental and theoretical study of the growth of sub-monolayer amounts of silicon (Si) on molybdenum disulfide (MoS2). At room temperature and low deposition rates we have found compelling evidence that the deposited Si atoms intercalate between the MoS2 layers. Our evidence relies on several experimental observations: (1) Upon the deposition of Si on pristine MoS2 the morphology of the surface transforms from a smooth surface to a hill-and-valley surface. The lattice constant of the hill-and-valley structure amounts to 3.16 Å, which is exactly the lattice constant of pristine MoS2. (2) The transitions from hills to valleys are not abrupt, as one would expect for epitaxial islands growing on-top of a substrate, but very gradual. (3) I(V) scanning tunneling spectroscopy spectra recorded at the hills and valleys reveal no noteworthy differences. (4) Spatial maps of dI/dz reveal that the surface exhibits a uniform work function and a lattice constant of 3.16 Å. (5) X-ray photo-electron spectroscopy measurements reveal that sputtering of the MoS2/Si substrate does not lead to a decrease, but an increase of the relative Si signal. Based on these experimental observations we have to conclude that deposited Si atoms do not reside on the MoS2 surface, but rather intercalate between the MoS2 layers. Our conclusion that Si intercalates upon the deposition on MoS2 is at variance with the interpretation by Chiappe et al. (Adv. Mater. 2014, 26, 2096–2101) that silicon forms a highly strained epitaxial layer on MoS2. Finally, density functional theory calculations indicate that silicene clusters encapsulated by MoS2 are stable.
Introduction
Since the discovery of graphene [1-4] interest has extended to the search for other 2D materials with properties similar to graphene. One appealing candidate is silicene, a graphene-like 2D allotrope of silicon. The first calculations of graphite-like allotropes of silicon and germanium were performed by Takeda and Shiraishi in 1994 [5]. These authors pointed out that two-dimensional silicon and germanium are not planar but buckled, i.e., the two sub-lattices of the honeycomb lattice are displaced with respect to each other in a direction normal to the two-dimensional sheet. In addition, the calculations of Takeda and Shiraishi [5] also revealed that silicene and germanene are semi-metals, like graphene. In 2007, Guzmán-Verri and Lew Yan Voon [6] performed tight-binding calculations of two-dimensional silicon. They pointed out that the graphite-like silicon sheet has linearly dispersing energy bands near the K points of the Brillouin zone, very comparable to graphene. Inspired by this analogy they put forward the name silicene for the two-dimensional silicon. Interestingly, the linear dispersing energy bands at the K points, the so-called Dirac cones, are robust against the buckling of the silicene lattice [5,7]. In 2009, Cahangirov et al. [7] found that germanene also exhibits similar properties as graphene and silicene.
Similar to graphene, the electrons near the Fermi level in free-standing silicene are predicted to behave as massless Dirac fermions [6]. The broken sub-lattice symmetry of silicene allows for the opening of a band gap in this material [8-12]. This band gap makes silicene a very appealing candidate for field-effect-based devices. Another attractive property of silicene is its spin–orbit coupling, which is substantially larger than the spin–orbit coupling in graphene [13,14].
Silicene does not occur in nature and therefore it has to be synthesized. Several studies have reported on the growth of a 2D silicon layer on Ag(111) [15-17]. Unfortunately, due to the strong coupling between Si ad-layer and Ag substrate, the interesting Dirac properties of silicene are destroyed [18]. Although a linear dispersion relation has been observed [17], it is argued by others that this band is related to the Ag substrate rather than to silicene [19] or to combined effects of silicene and the Ag(111) substrate [20,21]. Growth of silicon was also demonstrated on graphite, a van der Waals material, with the idea to suppress the interaction with the substrate and as such to preserve the Dirac properties [22]. Unfortunately, graphite is metallic, which could also affect the electronic bands of silicene in the vicinity of the Fermi level. Van der Waals materials with a band gap do not suffer from this limitation. Molybdenum disulfide (MoS2) is a member of the transition metal dichalcogenide (TMD) family that belongs to the class of van der Waals materials. Bulk MoS2 has a band gap of 1.29 eV, which increases to 1.90 eV for a monolayer of MoS2 [23]. This means that MoS2 has no states near the Fermi level and therefore hybridization with the energy bands of silicene near the Fermi level cannot occur. Recently, germanene, a 2D allotrope of germanium [24-28], has already been successfully grown on MoS2 [29]. Chiappe et al. [30] deposited Si on MoS2 and found that Si forms an epitaxially strained layer on top of MoS2 with a lattice constant identical to the MoS2 lattice constant, i.e., 3.16 Å. A study confirming the two-dimensionality of deposited Si on MoS2 has recently been carried out using variable-angle X-ray photoelectron spectroscopy (XPS) [31]. It should be pointed out here that this study showed that the S 2p3/2 peak in MoS2 is at around 167.6 eV, which is considerably higher than the pure core-level line of pure S. This high value might be an indication of contamination with O [32] or Ni [33].
Here we revisit the growth of Si on MoS2. Our scanning tunneling microscopy (STM) observations are very similar to those reported by Chiappe et al. [30]. However, we arrive at the conclusion that Si intercalates between the MoS2 layers. In order to verify our conclusion we have performed additional spectroscopic measurements. These additional spectroscopic measurements unambiguously reveal that sub-monolayer amounts of Si deposited on MoS2 at room temperature do not reside on top of MoS2, but intercalate between the MoS2 layers.
Experimental
The scanning tunneling microscopy and spectroscopy measurements were performed with an Omicron STM-1 room-temperature scanning tunneling microscope in ultra-high vacuum (UHV). The UHV system is composed of three separate chambers: a load-lock chamber for a quick entry of new samples and STM tips, a preparation chamber with facilities for sample heating, ion bombardment and evaporation of silicon and an STM chamber. The base pressures in the STM chamber and the preparation chamber are below 3 × 10−11 mbar and 5 × 10−11 mbar, respectively. The MoS2 samples are purchased from HQ graphene. Prior to inserting the samples into the lock-load system they were cleaned by mechanical exfoliation. Silicon was deposited on the MoS2 samples using a custom-built Si evaporator, which consists of a small piece of a Si wafer that can be heated resistively. The distance between substrate and evaporator is about 10 cm. The silicon was deposited at a rather low deposition rate of 0.8 nm·h−1. The silicon evaporator was calibrated by depositing a sub-monolayer amount of Si on a Ge(001) substrate. The Ge(001) surface was cleaned by applying several cycles of Ar ion sputtering and annealing. After deposition and mild annealing at a temperature of 450–500 K, the Ge(001) substrate was inserted into the STM and subsequently the areal coverage of the epitaxial Si islands was determined. I(V) curves are recorded at constant height at 450 ms per curve. Spatial maps of dI/dz are measured using a lock-in amplifier. A small high frequency (ca. 1.9 kHz) sinusoidal signal is added to the z-piezo and the tunnel current is fed into the lock-in amplifier. The output signal of the lock-in amplifier, which is proportional to dI/dz, is measured simultaneously with the topography.
MoS2 samples used for the X-ray photoelectron spectroscopy (XPS) experiments were purchased from nanoScience Instruments. The MoS2 samples were exfoliated before Si deposition. In a separate UHV chamber, Si was deposited on the MoS2 sample via resistive heating of a small piece of a silicon wafer and then the MoS2 sample was quickly transferred to the XPS chamber. During this transfer the sample was exposed to ambient conditions. The deposited amount of Si was 0.5 monolayers. The base pressure of both chambers is below 4 × 10−10 mbar. Both MoS2 and Si/MoS2 samples were measured with a monochromatic Al Kα (1486.6 eV) X-ray source with a pass energy of 89.5 eV and 35.75 eV for survey and high-resolution scans, respectively. During the XPS measurements, the pressure was kept at or below 1 × 10−9 mbar. The angle between the X-ray source, which is aligned along the surface normal, and spectrometer is 54.7°. All XPS core-level spectra were analyzed using Augerscan software, which is equipped with its own curve-fitting program. The core-level peaks are fitted using a Gaussian–Lorentzian (GL) function to include the instrumental response function along with the core-level line shape. The secondary-electron background was subtracted using a Shirley function [34]. The energy differences between the 3d and 2p spin–orbit couples were set to 3.13 eV and 1.18 eV, respectively. The ratios of the areas of the doublet peaks were also fixed. During sputtering the pressure is increased to 3 × 10−8 mbar by leaking in Ar gas while the pressure around the filament in the differentially pumped argon gas chamber increased to 1 × 10−4 mbar. The sample was sputtered with a beam of Ar ions with 1 kV energy. The emission current used was 25 mA, which resulted in an ion current of 0.33 μA. The shape of the beam is circular with a diameter of approximately 2 mm.
First-principles calculations are based on the projector-augmented wave (PAW) method [35,36] within DFT as implemented in the Vienna ab initio simulation package (VASP) [37]. The exchange–correlation interactions are treated using the generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) formulation [38]. The plane waves are expanded with an energy cut of 400 eV. Since the semi-local functionals, such as GGA, fail to describe weakly interacting systems, we also take into account the van der Waals interaction [39,40]. Brillouin-zone integrations for structure relaxations are approximated by using the special k-point sampling of the Monkhorst–Pack scheme with a Γ-centered 3 × 3 × 1 grid [41]. In order to minimize the periodic interactions along the z-direction (the direction perpendicular to the plane of the hetero-trilayer) the vacuum space between the layers has a width of at least 15 Å.
Results and Discussion
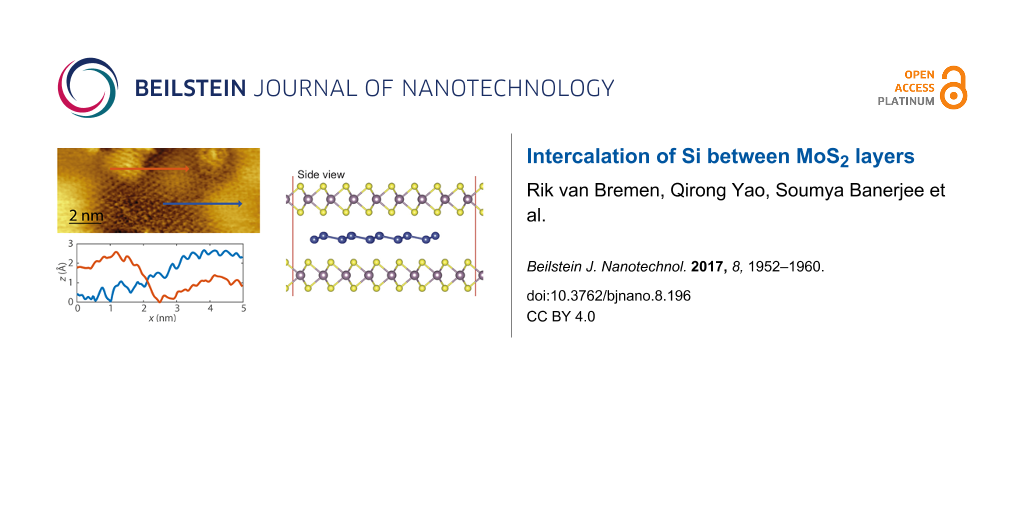
In Figure 1, STM images of pristine MoS2 and MoS2 after the deposition of ca. 0.2 monolayers of Si at room temperature are shown. The pristine MoS2 surface appears very smooth. Usually only the top sulfur layer is resolved, resulting in a lattice with hexagonal symmetry and a lattice constant of 3.16 Å (see Figure 1b,c). The pristine MoS2 contains some intrinsic defects, which are visible as dark depressions as indicated by the arrow in Figure 1a. These defects are most probably caused by vacancies or interstitials and have been found to exhibit a metal-like behavior [42,43]. Upon the deposition of 0.2 monolayers of Si, the surface morphology converts to a hill-and-valley structure as shown in Figure 1d. The arrows indicate a bright hill and a dark valley. Upon further deposition of silicon, the surface becomes rougher and more difficult to scan as shown in Figure S1 in Supporting Information File 1. When even more silicon is deposited, silicon clusters on top of MoS2 become visible. A close-up image of the transition of a hill to a valley is represented in Figure 1e. The line profiles indicated in the figure correspond to the cross sections shown in Figure 1f. The typical height variation of a transition is found to be of several angstroms. We found a similar height variation using density functional theory (DFT) calculations of the intercalation of a single silicon layer in between two MoS2 layers. These calculations are discussed after the presentation of the experimental results. It is immediately obvious from Figure 1f that the transition from a hill to a valley is very gradual. Interestingly, the lattice constant of the hill-and-valley structure is identical to the lattice constant of pristine MoS2, i.e. 3.16 Å. Both observations are similar to the observations reported by Chiappe et al. [30] who deposited 0.8 monolayers of silicon on MoS2 (obtained from SPI) at 200 °C. Based on these observations Chiappe et al. [30] concluded that Si grows epitaxially on MoS2 with a lattice constant that is identical to MoS2. This implies that the Si layer is highly strained, indicative of a rather strong interaction between MoS2 and Si. This seems unlikely, bearing in mind that MoS2 is a van der Waals material. We tentatively put forward another interpretation, namely that Si intercalates between the MoS2 layers. The gradual transition from a hill to a valley as well as the observation of the MoS2 lattice constant after Si deposition nicely fits into this picture.
![[2190-4286-8-196-1]](/bjnano/content/figures/2190-4286-8-196-1.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 1: (a) STM image of pristine MoS2 taken prior to the deposition of Si. The arrow indicates an intrinsic defect, which is often found on MoS2. (b) High-resolution STM image of pristine MoS2. (c) Fast Fourier-transform of pristine MoS2 showing the hexagonal symmetry. (d) STM image taken after the deposition of 0.2 monolayers of Si. The arrows indicate a hill (bright) and a valley (dark). (e) High-resolution STM image taken after the deposition of 0.2 monolayers of Si. (f) Line scans taken along the lines indicated in panel (e). The sample bias is 1.2V and the tunnelling current is 0.5 nA.
Figure 1: (a) STM image of pristine MoS2 taken prior to the deposition of Si. The arrow indicates an intrinsi...
In order to verify our interpretation we have performed additional scanning tunneling spectroscopy (STS) measurements. I(V) scanning tunneling spectra were recorded at the hills and valleys as indicated by the arrows in Figure 1d. Average spectroscopy curves of a hill and of a valley, which in total are comprised of 3500 spectra, are displayed in Figure 2. The I(V) spectra are almost identical to each other. The small difference between both curves might be a residual effect of Si residing underneath the MoS2 layer. If the top layer were a silicon cluster the I(V) spectra would differ significantly as is shown in Figure S2 in Supporting Information File 1.
![[2190-4286-8-196-2]](/bjnano/content/figures/2190-4286-8-196-2.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 2: STS recorded at the hills (black curve) and at the valleys (red curve). Set points sample bias 1.2 V and tunnel current 0.5 nA.
Figure 2: STS recorded at the hills (black curve) and at the valleys (red curve). Set points sample bias 1.2 ...
In order to remove the large-scale height variation from the topography scan, we simultaneously recorded a spatial map of dI/dz (Figure 3). The dI/dz signal only depends on the effective work function, also referred to as the apparent barrier height, and not on any large-scale height variations [44,45]. It should be pointed out here that spatial maps of dI/dz often exhibit a resolution that is similar to normal topographic STM images without, of course, the large-scale height variations [44].
![[2190-4286-8-196-3]](/bjnano/content/figures/2190-4286-8-196-3.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 3: (a) STM image of a MoS2 surface after the deposition of 0.2 monolayers of Si. (b) Spatial map of dI/dz. In both images the atomic structure is resolved. (c) Line- scan taken along the dotted line depicted in panel (a). Sample bias is 1.2 V and tunnel current is 0.5 nA.
Figure 3: (a) STM image of a MoS2 surface after the deposition of 0.2 monolayers of Si. (b) Spatial map of dI...
The results shown in Figure 3 make clear two points. First, since height information is not present in a dI/dz map we have to conclude that the surface is smooth and continuous. Second, dI/dz provides information on the apparent barrier height, which is a material property. No contrast is visible and therefore we have to conclude that we are dealing with the same material, i.e., MoS2. Both these points provide compelling evidence that the deposited Si intercalates between the MoS2 layers. For a comparable system, namely Si on WSe2, we recently arrived at a similar conclusion [45].
XPS measurements have been performed to obtain insight of the chemical composition of the top layers. Before depositing Si, XPS measurements were carried out on pristine MoS2 in order to find the exact positions of the Mo 3d5/2 and S 2p3/2 core-level peaks. (Figure 4a and Figure 4b, respectively). The Mo 3d5/2 and S 2p3/2 peaks were measured at 230.25 eV and 163.09 eV, respectively. The location of these peaks is in good agreement with [46,47].
![[2190-4286-8-196-4]](/bjnano/content/figures/2190-4286-8-196-4.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 4: Core-level spectra of (a) Mo and (b) S before depositing Si. The spectra are fitted with two GL function peaks. In (a), 1 and 2 represent the Mo 3d5/2 and 3d3/2 peaks, respectively. In (b), 1 and 2 represent the S 2p3/2 and 2p1/2 peaks, respectively. In both figures, the resultant fitted spectra are represented by an orange line.
Figure 4: Core-level spectra of (a) Mo and (b) S before depositing Si. The spectra are fitted with two GL fun...
The core-level spectra of Si, Mo and S after the deposition of 0.5 monolayers of Si on MoS2 are shown in Figure 5a, Figure 5b and Figure 5c, respectively. A higher coverage than in the case of STM is used in order to yield a stronger signal in the XPS measurements. STM topography images with a higher coverage can be found in Figure S1 in Supporting Information File 1. The XPS data show two peaks associated with Si. The smaller peak, located at 98.13 eV, can be attributed to pristine Si. The other peak, measured at 103 eV, can be attributed to oxidized silicon [48]. The oxidation of Si occurs during the transfer of the sample from the growth chamber to the XPS chamber. During this transfer the sample was exposed to ambient conditions. A more detailed analysis reveals that only 5% of the Si is pristine, whereas the rest is oxidized. Upon sputtering of the MoS2/Si sample with an Ar ion beam with 1 kV energy, we observe that the relative Si signal increases while the relative S signal decreases as can be seen in Figure S3 in Supporting Information File 1. This observation indicates that Si has intercalated between the MoS2 layers. In addition, we also conclude that the intercalated Si can be oxidized.
![[2190-4286-8-196-5]](/bjnano/content/figures/2190-4286-8-196-5.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 5: Core-level spectra of (a) Si, (b) Mo and (c) S after depositing Si. The peak-fitting procedure is the same as in Figure 4. In panel (a) a small peak at around 98.1 eV was needed to fit the tail of the peak at the lower-energy side. Orange lines represent the resultant fitted spectra.
Figure 5: Core-level spectra of (a) Si, (b) Mo and (c) S after depositing Si. The peak-fitting procedure is t...
It is well known that numerous elements have a strong tendency to intercalate between MoS2 layers [49,50]. As for the intercalation mechanism of silicon in between MoS2 layers, we can only speculate. A plethora of studies on the intercalation of different chemical species in TMDs have been reported from elements as small as lithium [51], sodium [52-54] and carbon [55] to elements as large as cesium [56,57] and gold [58]. Other studies report on the intercalation of silicon and other elements under graphene layers synthesized on metal substrates [59-61].
The driving force for intercalation is charge transfer between the intercalated atoms and the layered material [62,63] or thermodynamic stabilization [61,62]. The mechanism of intercalation was found to occur through cracks and wrinkles in the layers [60] and via edges [51]. Because the diffusion barrier of adsorbed silicon atoms on top of MoS2 is assumed to be very low and the experiments are performed at room temperature, it is expected that silicon adatoms can easily diffuse over the surface to reach these cracks, wrinkles and step edges.
In order to study the effect of the oxidation of intercalated silicon in more detail we measured the exact positions of the Mo 3d5/2 and S 2p3/2 peaks. Both peaks shift to a lower binding energy by about 0.45 eV. This shift cannot be interpreted as a simple chemical shift due to a chemical reaction of the involved elements, i.e., Mo/S/Si and O [64]. In addition, after the deposition of Si no significant changes in the FWHM of the peaks of Mo (0.97 before, 1.13 after) as well as of S (1.09 before, 1.21 after) were observed, indicating that no chemical reaction between MoS2 and silicon oxide has occurred. It is very likely that the observed shift is attributed to a change in the position of the Fermi level.
It has been shown that the deposition of MoS2 on a SiO2 substrate with interface impurities leads to a charge transfer from the MoS2 surface to the defect states and, thus, to the formation of surface dipoles [65]. These dipoles shift the Fermi level of MoS2 closer to the valence band maximum (p-type). The shift of the Fermi level also leads to a shift in the binding energy of the Mo and S peaks to lower binding energies.
Next, we will discuss the results of our density functional theory calculations regarding the intercalated Si. To be consistent with experimental results we have fixed the lattice constant of MoS2 to 3.16 Å. We first calculated the structural and electronic properties of hetero-trilayers composed of a silicene layer intercalated between two MoS2 monolayers (MoS2–silicene–MoS2). Due to the large lattice mismatch, we have considered a commensurable supercell, in which we have placed a 5 × 5 silicene cell and a 6 × 6 MoS2 cell on top of each other. For this configuration the lattice mismatch of the MoS2–silicene–MoS2 trilayer becomes less than 1%. Figure 6 shows the optimized structure of the MoS2–silicene–MoS2 hetero-trilayer. The calculated interlayer distance in a pristine MoS2 bilayer is found to be 3.00 Å. Insertion of a silicene monolayer enlarges the interlayer separation between MoS2 layers from 3 Å to 6.52 Å, corresponding to an increase of the interlayer separation of 3.52 Å.
![[2190-4286-8-196-6]](/bjnano/content/figures/2190-4286-8-196-6.png?scale=2.0&max-width=1024&background=FFFFFF)
Figure 6: Top and side views of silicene intercalated in bilayer MoS2.
Figure 6: Top and side views of silicene intercalated in bilayer MoS2.
In order to study the possible formation of silicene between the MoS2 monolayers, we consider a buckled 2D silicon cluster (Si37) consisting of six-membered silicon rings. We used a 7 × 7 super-cell structure for the MoS2 bilayer. Initial and equilibrium geometries for both a free-standing as well as the intercalated silicon cluster inserted between the MoS2 layers are shown in Figure 7. We found that a free-standing 2D buckled silicon cluster is, in contrast to an infinite silicene layer, not even metastable in vacuum and spontaneously transforms into a strongly buckled 3D assembly as seen in Figure 7a. The intercalated silicon cluster in Figure 7b also undergoes a remarkable structural reconstruction. The optimized structure of a silicon cluster encapsulated between two MoS2 layers is totally different from the free-standing optimized silicon cluster in vacuum. This is noticeable in that the shape of the hexagons is not uniform as is the case for silicene. Especially at the edges, due to the presence of the Si dangling bonds, the hexagons are seriously distorted. However, intercalation between MoS2 layers preserves the 2D buckled structure of the silicon cluster during the structure relaxation. Thus, we suggest that the intercalation of silicon atoms between MoS2 layers may promote the formation of silicene, which interacts only weakly with the environment via van der Waals forces. We found that both top and bottom MoS2 layers develop bumps due to the interaction with the silicon cluster. The average interlayer MoS2 distance varies within the range of 5.5–6.2 Å, which corresponds to an increase in interlayer separation of 2.5-3.2 Å. This agrees well with the measured height variation.
![[2190-4286-8-196-7]](/bjnano/content/figures/2190-4286-8-196-7.png?scale=1.84&max-width=1024&background=FFFFFF)
Figure 7: Initial (left) and equilibrium (right) structure of (a) a free standing and (b) an intercalated silicon cluster (Si37).
Figure 7: Initial (left) and equilibrium (right) structure of (a) a free standing and (b) an intercalated sil...
Conclusion
In this work we revisited the growth of Si on MoS2. STM topography data reveals that Si does not grow on top of the MoS2 substrate, but rather intercalates in between the MoS2 layers. It is known that layered materials such as MoS2 have a tendency to host intercalants. In this work we provide additional evidence for silicon intercalation by using STS and XPS. Since silicon intercalates it is interesting to scrutinize if there are possibilities to grow a 2D layer in between two layers of MoS2. Our density functional theory calculations show that 2D silicon clusters intercalated between MoS2 layers are stable.
Supporting Information
| Supporting Information File 1: Additional experimental data. | ||
| Format: PDF | Size: 332.4 KB | Download |
Acknowledgements
R.v.B. and H.J.W.Z. thank the Dutch organization for scientific research NWO for financial support (FV157 14TWDO07). Q.Y. thanks the China Scholarship Council for financial support. D.C. and N.O. thank ND EPSCoR (#UND0021231, #UND0014095) and UND for financial support. The computer resources used in this work are provided by the Computational Research Center (HPC-Linux cluster) at UND.
References
-
Novoselov, K. S.; Geim, A. K.; Morozov, S. V.; Jiang, D.; Zhang, Y.; Dubonos, S. V.; Grigorieva, I. V.; Firsov, A. A. Science 2004, 306, 666–669. doi:10.1126/science.1102896
Return to citation in text: [1] -
Zhang, Y.; Tan, Y.-W.; Stormer, H. L.; Kim, P. Nature 2005, 438, 201–204. doi:10.1038/nature04235
Return to citation in text: [1] -
Ohta, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Science 2006, 313, 951–954. doi:10.1126/science.1130681
Return to citation in text: [1] -
Castro Neto, A. H.; Guinea, F.; Peres, N. M. R.; Novoselov, K. S.; Geim, A. K. Rev. Mod. Phys. 2009, 81, 109–162. doi:10.1103/RevModPhys.81.109
Return to citation in text: [1] -
Takeda, K.; Shiraishi, K. Phys. Rev. B 1994, 50, 14916–14922. doi:10.1103/PhysRevB.50.14916
Return to citation in text: [1] [2] [3] -
Guzmán-Verri, G. G.; Lew Yan Voon, L. C. Phys. Rev. B 2007, 76, 075131. doi:10.1103/PhysRevB.76.075131
Return to citation in text: [1] [2] -
Cahangirov, S.; Topsakal, M.; Aktürk, E.; Şahin, H.; Ciraci, S. Phys. Rev. Lett. 2009, 102, 236804. doi:10.1103/PhysRevLett.102.236804
Return to citation in text: [1] [2] -
Song, Y.-L.; Zhang, S.; Lu, D.-B.; Xu, H.-r.; Wang, Z.; Zhang, Y.; Lu, Z.-W. Eur. Phys. J. B 2013, 86, 488. doi:10.1140/epjb/e2013-31078-4
Return to citation in text: [1] -
Quhe, R.; Fei, R.; Liu, Q.; Zheng, J.; Li, H.; Xu, C.; Ni, Z.; Wang, Y.; Yu, D.; Gao, Z.; Lu, J. Sci. Rep. 2012, 2, 853. doi:10.1038/srep00853
Return to citation in text: [1] -
Ni, Z.; Liu, Q.; Tang, K.; Zheng, J.; Zhou, J.; Qin, R.; Gao, Z.; Yu, D.; Lu, J. Nano Lett. 2012, 12, 113–118. doi:10.1021/nl203065e
Return to citation in text: [1] -
Gao, N.; Li, J. C.; Jiang, Q. Phys. Chem. Chem. Phys. 2014, 16, 11673. doi:10.1039/C4CP00089G
Return to citation in text: [1] -
Drummond, N. D.; Zólyomi, V.; Fal’ko, V. I. Phys. Rev. B 2012, 85, 075423. doi:10.1103/PhysRevB.85.075423
Return to citation in text: [1] -
Kane, C. L.; Mele, E. J. Phys. Rev. Lett. 2005, 95, 226801. doi:10.1103/PhysRevLett.95.226801
Return to citation in text: [1] -
Lew Yan Voon, L. C. Chin. Phys. B 2015, 24, 087309. doi:10.1088/1674-1056/24/8/087309
Return to citation in text: [1] -
Lalmi, B.; Oughaddou, H.; Enriquez, H.; Kara, A.; Vizzini, S.; Ealet, B.; Aufray, B. Appl. Phys. Lett. 2010, 97, 223109. doi:10.1063/1.3524215
Return to citation in text: [1] -
Jamgotchian, H.; Colignon, Y.; Hamzaoui, N.; Ealet, B.; Hoarau, J. Y.; Aufray, B.; Bibérian, J. P. J. Phys.: Condens. Matter 2012, 24, 172001. doi:10.1088/0953-8984/24/17/172001
Return to citation in text: [1] -
Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M. C.; Resta, A.; Ealet, B.; Le Lay, G. Phys. Rev. Lett. 2012, 108, 155501. doi:10.1103/PhysRevLett.108.155501
Return to citation in text: [1] [2] -
Lin, C.-L.; Arafune, R.; Kawahara, K.; Kanno, M.; Tsukahara, N.; Minamitani, E.; Kim, Y.; Kawai, M.; Takagi, N. Phys. Rev. Lett. 2013, 110, 076801. doi:10.1103/PhysRevLett.110.076801
Return to citation in text: [1] -
Chen, M. X.; Weinert, M. Nano Lett. 2014, 14, 5189–5193. doi:10.1021/nl502107v
Return to citation in text: [1] -
Feng, Y.; Liu, D.; Feng, B.; Liu, X.; Zhao, L.; Xie, Z.; Liu, Y.; Liang, A.; Hu, C.; Hu, Y.; He, S.; Liu, G.; Zhang, J.; Chen, C.; Xu, Z.; Chen, L.; Wu, K.; Liu, Y.-T.; Lin, H.; Huang, Z.-Q.; Hsu, C.-H.; Chuang, F.-C.; Bansil, A.; Zhou, X. J. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 14656–14661. doi:10.1073/pnas.1613434114
Return to citation in text: [1] -
Fleurence, A.; Friedlein, R.; Ozaki, T.; Kawai, H.; Wang, Y.; Yamada-Takamura, Y. Phys. Rev. Lett. 2012, 108, 245501. doi:10.1103/PhysRevLett.108.245501
Return to citation in text: [1] -
De Crescenzi, M.; Berbezier, I.; Scarselli, M.; Castrucci, P.; Abbarchi, M.; Ronda, A.; Jardali, F.; Park, J.; Vach, H. ACS Nano 2016, 10, 11163–11171. doi:10.1021/acsnano.6b06198
Return to citation in text: [1] -
Mak, K. F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T. F. Phys. Rev. Lett. 2010, 105, 136805. doi:10.1103/PhysRevLett.105.136805
Return to citation in text: [1] -
Li, L.; Lu, S.; Pan, J.; Qin, Z.; Wang, Y.; Wang, Y.; Cao, G.; Du, S.; Gao, H.-J. Adv. Mater. 2014, 26, 4820–4824. doi:10.1002/adma.201400909
Return to citation in text: [1] -
Dávila, M. E.; Xian, L.; Cahangirov, S.; Rubio, A.; Le Lay, G. New J. Phys. 2014, 16, 095002. doi:10.1088/1367-2630/16/9/095002
Return to citation in text: [1] -
Bampoulis, P.; Zhang, L.; Safaei, A.; van Gastel, R.; Poelsema, B.; Zandvliet, H. J. W. J. Phys.: Condens. Matter 2014, 26, 442001. doi:10.1088/0953-8984/26/44/442001
Return to citation in text: [1] -
Zhang, L.; Bampoulis, P.; van Houselt, A.; Zandvliet, H. J. W. Appl. Phys. Lett. 2015, 107, 111605. doi:10.1063/1.4931102
Return to citation in text: [1] -
Acun, A.; Zhang, L.; Bampoulis, P.; Farmanbar, M.; van Houselt, A.; Rudenko, A. N.; Lingenfelder, M.; Brocks, G.; BPoelsema, K.; atsnelson, M. I.; Zandvliet, H. J. W. J. Phys.: Condens. Matter 2015, 27, 443002. doi:10.1088/0953-8984/27/44/443002
Return to citation in text: [1] -
Zhang, L.; Bampoulis, P.; Rudenko, A. N.; Yao, Q.; van Houselt, A.; Poelsema, B.; Katsnelson, M. I.; Zandvliet, H. J. W. Phys. Rev. Lett. 2016, 116, 256804. doi:10.1103/PhysRevLett.116.256804
Return to citation in text: [1] -
Chiappe, D.; Scalise, E.; Cinquanta, E.; Grazianetti, C.; van den Broek, B.; Fanciulli, M.; Houssa, M.; Molle, A. Adv. Mater. 2014, 26, 2096–2101. doi:10.1002/adma.201304783
Return to citation in text: [1] [2] [3] [4] -
Molle, A.; Lamperti, A.; Rotta, D.; Fanciulli, M.; Cinquanta, E.; Grazianetti, C. Adv. Mater. Interfaces 2016, 3, 1500619. doi:10.1002/admi.201500619
Return to citation in text: [1] -
Wagner, C. D.; Taylor, J. A. J. Electron Spectrosc. Relat. Phenom. 1982, 28, 211–217. doi:10.1016/0368-2048(82)85044-5
Return to citation in text: [1] -
Yu, X.-R.; Liu, F.; Wang, Z.-Y.; Chen, Y. J. Electron Spectrosc. Relat. Phenom. 1990, 50, 159–166. doi:10.1016/0368-2048(90)87059-W
Return to citation in text: [1] -
Briggs, D.; Seah, M. P. Practical Surface Analysis by Auger and X-Ray Photoelectron Spectroscopy; John Wiley & Sons Ltd: New York, NY, U.S.A., 1983.
Return to citation in text: [1] -
Kresse, G.; Furthmüller, J. Phys. Rev. B 1996, 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Return to citation in text: [1] -
Blöchl, P. E. Phys. Rev. B 1994, 50, 17953–17979. doi:10.1103/PhysRevB.50.17953
Return to citation in text: [1] -
Kresse, G.; Joubert, D. Phys. Rev. B 1999, 59, 1758–1775. doi:10.1103/PhysRevB.59.1758
Return to citation in text: [1] -
Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys. Rev. Lett. 1996, 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Return to citation in text: [1] -
Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. J. Chem. Phys. 2010, 132, 154104. doi:10.1063/1.3382344
Return to citation in text: [1] -
Grimme, S.; Ehrlich, S.; Goerigk, L. J. Comput. Chem. 2011, 32, 1456–1465. doi:10.1002/jcc.21759
Return to citation in text: [1] -
Monkhorst, H. J.; Pack, J. D. Phys. Rev. B 1976, 13, 5188–5192. doi:10.1103/PhysRevB.13.5188
Return to citation in text: [1] -
Addou, R.; Colombo, L.; Wallace, R. M. ACS Appl. Mater. Interfaces 2015, 7, 11921–11929. doi:10.1021/acsami.5b01778
Return to citation in text: [1] -
Bampoulis, P.; van Bremen, R.; Yao, Q.; Poelsema, B.; Zandvliet, H. J. W.; Sotthewes, K. ACS Appl. Mater. Interfaces 2017, 9, 19278–19286. doi:10.1021/acsami.7b02739
Return to citation in text: [1] -
Wiesendanger, R. Scanning Probe Microscopy and Spectroscopy: Methods and Applications; Cambridge University Press: Cambridge, United Kingdom, 1994. doi:10.1017/CBO9780511524356
Return to citation in text: [1] [2] -
Yao, Q.; van Bremen, R.; Zandvliet, H. J. W. Appl. Phys. Lett. 2016, 109, 243105. doi:10.1063/1.4972036
Return to citation in text: [1] [2] -
Lince, J. R.; Carré, D. J.; Fleischauer, P. D. Effects of Argon-Ion Bombardment on the Basal Plan Surface of MoS2 – Report Sd-TR-86-95; Space Division, Air Force Systems Command: Los Angeles, CA, U.S.A., 1987.
Return to citation in text: [1] -
Vissers, J. P. R.; Groot, C. K.; van Oers, E. M.; Beer, D.; Prins, R. Bull. Soc. Chim. Belg. 1984, 93, 813–822. doi:10.1002/bscb.19840930822
Return to citation in text: [1] -
Finster, J.; Klinkenberg, E.-D.; Heeg, J.; Braun, W. Vacuum 1990, 41, 1586–1589. doi:10.1016/0042-207X(90)94025-L
Return to citation in text: [1] -
Benavente, E.; Santa Ana, M. A.; Mendizábal, F.; González, G. Coord. Chem. Rev. 2002, 224, 87–109. doi:10.1016/S0010-8545(01)00392-7
Return to citation in text: [1] -
Vázquez, A. Mater. Lett. 1998, 35, 22–27. doi:10.1016/S0167-577X(97)00224-3
Return to citation in text: [1] -
Xiong, F.; Wang, H.; Liu, X.; Sun, J.; Brongersma, M.; Pop, E.; Cui, Y. Nano Lett. 2015, 15, 6777–6784. doi:10.1021/acs.nanolett.5b02619
Return to citation in text: [1] [2] -
Brauer, H. E.; Ekvall, I.; Olin, H.; Starnberg, H. I.; Wahlström, E.; Hughes, H. P.; Strocov, V. N. Phys. Rev. B 1997, 55, 10022. doi:10.1103/PhysRevB.55.10022
Return to citation in text: [1] -
Brauer, H. E.; Starnberg, H. I.; Holleboom, L. J.; Strocov, V. N.; Hughes, H. P. Phys. Rev. B 1998, 58, 10031–10045. doi:10.1103/PhysRevB.58.10031
Return to citation in text: [1] -
Ekvall, I.; Brauer, H. E.; Wahlström, E.; Olin, H. Phys. Rev. B 1999, 59, 7751. doi:10.1103/PhysRevB.59.7751
Return to citation in text: [1] -
Kwieciñski, W.; Sotthewes, K.; Poelsema, B.; Zandvliet, H. J. W.; Bampoulis, P. J. Colloid Interface Sci. 2017, 505, 776–782. doi:10.1016/j.jcis.2017.06.076
Return to citation in text: [1] -
Pettenkofer, C.; Jaegermann, W.; Schellenberger, A.; Holub-Krappe, E.; Papageorgopoulos, C. A.; Kamaratos, M.; Papageorgopoulos, A. Solid State Commun. 1992, 84, 921–926. doi:10.1016/0038-1098(92)90459-M
Return to citation in text: [1] -
Starnberg, H. I.; Brauer, H. E.; Holleboom, L. J.; Hughes, H. P. Phys. Rev. Lett. 1993, 70, 3111–3114. doi:10.1103/PhysRevLett.70.3111
Return to citation in text: [1] -
Iyikanat, F.; Sahin, H.; Senger, R. T.; Peeters, F. M. APL Mater. 2014, 2, 092801. doi:10.1063/1.4893543
Return to citation in text: [1] -
Meng, L.; Wu, R.; Zhou, H.; Li, G.; Zhang, Y.; Li, L.; Wang, Y.; Gao, H.-J. Appl. Phys. Lett. 2012, 100, 083101. doi:10.1063/1.3687688
Return to citation in text: [1] -
Petrović, M.; Šrut Rakić, I.; Runte, S.; Busse, C.; Sadowski, J. T.; Lazić, P.; Pletikosić, I.; Pan, Z.-H.; Milun, M.; Pervan, P.; Atodiresei, N.; Brako, R.; Šokčević, D.; Valla, T.; Michely, T.; Kralj, M. Nat. Commun. 2013, 4, 2772. doi:10.1038/ncomms3772
Return to citation in text: [1] [2] -
Li, G.; Zhou, H.; Pan, L.; Zhang, Y.; Huang, L.; Xu, W.; Du, S.; Ouyang, M.; Ferrari, A. C.; Gao, H.-J. J. Am. Chem. Soc. 2015, 137, 7099–7103. doi:10.1021/ja5113657
Return to citation in text: [1] [2] -
Whittingham, M. S.; Chianelli, R. R. J. Chem. Educ. 1980, 57, 569. doi:10.1021/ed057p569
Return to citation in text: [1] [2] -
Odink, D. A.; Song, K.; Kauzlarich, S. M. Chem. Mater. 1992, 4, 906–911. doi:10.1021/cm00022a029
Return to citation in text: [1] -
NIST X-ray Photoelectron Spectroscopy (XPS) Database, Version 3.5. https://srdata.nist.gov/xps/Default.aspx (accessed June 27, 2017).
Return to citation in text: [1] -
Dolui, K.; Rungger, I.; Sanvito, S. Phys. Rev. B 2013, 87, 165402. doi:10.1103/PhysRevB.87.165402
Return to citation in text: [1]
| 39. | Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. J. Chem. Phys. 2010, 132, 154104. doi:10.1063/1.3382344 |
| 40. | Grimme, S.; Ehrlich, S.; Goerigk, L. J. Comput. Chem. 2011, 32, 1456–1465. doi:10.1002/jcc.21759 |
| 41. | Monkhorst, H. J.; Pack, J. D. Phys. Rev. B 1976, 13, 5188–5192. doi:10.1103/PhysRevB.13.5188 |
| 42. | Addou, R.; Colombo, L.; Wallace, R. M. ACS Appl. Mater. Interfaces 2015, 7, 11921–11929. doi:10.1021/acsami.5b01778 |
| 43. | Bampoulis, P.; van Bremen, R.; Yao, Q.; Poelsema, B.; Zandvliet, H. J. W.; Sotthewes, K. ACS Appl. Mater. Interfaces 2017, 9, 19278–19286. doi:10.1021/acsami.7b02739 |
| 48. | Finster, J.; Klinkenberg, E.-D.; Heeg, J.; Braun, W. Vacuum 1990, 41, 1586–1589. doi:10.1016/0042-207X(90)94025-L |
| 49. | Benavente, E.; Santa Ana, M. A.; Mendizábal, F.; González, G. Coord. Chem. Rev. 2002, 224, 87–109. doi:10.1016/S0010-8545(01)00392-7 |
| 50. | Vázquez, A. Mater. Lett. 1998, 35, 22–27. doi:10.1016/S0167-577X(97)00224-3 |
| 45. | Yao, Q.; van Bremen, R.; Zandvliet, H. J. W. Appl. Phys. Lett. 2016, 109, 243105. doi:10.1063/1.4972036 |
| 46. | Lince, J. R.; Carré, D. J.; Fleischauer, P. D. Effects of Argon-Ion Bombardment on the Basal Plan Surface of MoS2 – Report Sd-TR-86-95; Space Division, Air Force Systems Command: Los Angeles, CA, U.S.A., 1987. |
| 47. | Vissers, J. P. R.; Groot, C. K.; van Oers, E. M.; Beer, D.; Prins, R. Bull. Soc. Chim. Belg. 1984, 93, 813–822. doi:10.1002/bscb.19840930822 |
| 44. | Wiesendanger, R. Scanning Probe Microscopy and Spectroscopy: Methods and Applications; Cambridge University Press: Cambridge, United Kingdom, 1994. doi:10.1017/CBO9780511524356 |
| 45. | Yao, Q.; van Bremen, R.; Zandvliet, H. J. W. Appl. Phys. Lett. 2016, 109, 243105. doi:10.1063/1.4972036 |
| 44. | Wiesendanger, R. Scanning Probe Microscopy and Spectroscopy: Methods and Applications; Cambridge University Press: Cambridge, United Kingdom, 1994. doi:10.1017/CBO9780511524356 |
| 30. | Chiappe, D.; Scalise, E.; Cinquanta, E.; Grazianetti, C.; van den Broek, B.; Fanciulli, M.; Houssa, M.; Molle, A. Adv. Mater. 2014, 26, 2096–2101. doi:10.1002/adma.201304783 |
| 30. | Chiappe, D.; Scalise, E.; Cinquanta, E.; Grazianetti, C.; van den Broek, B.; Fanciulli, M.; Houssa, M.; Molle, A. Adv. Mater. 2014, 26, 2096–2101. doi:10.1002/adma.201304783 |
| 51. | Xiong, F.; Wang, H.; Liu, X.; Sun, J.; Brongersma, M.; Pop, E.; Cui, Y. Nano Lett. 2015, 15, 6777–6784. doi:10.1021/acs.nanolett.5b02619 |
| 52. | Brauer, H. E.; Ekvall, I.; Olin, H.; Starnberg, H. I.; Wahlström, E.; Hughes, H. P.; Strocov, V. N. Phys. Rev. B 1997, 55, 10022. doi:10.1103/PhysRevB.55.10022 |
| 53. | Brauer, H. E.; Starnberg, H. I.; Holleboom, L. J.; Strocov, V. N.; Hughes, H. P. Phys. Rev. B 1998, 58, 10031–10045. doi:10.1103/PhysRevB.58.10031 |
| 54. | Ekvall, I.; Brauer, H. E.; Wahlström, E.; Olin, H. Phys. Rev. B 1999, 59, 7751. doi:10.1103/PhysRevB.59.7751 |
| 55. | Kwieciñski, W.; Sotthewes, K.; Poelsema, B.; Zandvliet, H. J. W.; Bampoulis, P. J. Colloid Interface Sci. 2017, 505, 776–782. doi:10.1016/j.jcis.2017.06.076 |
| 51. | Xiong, F.; Wang, H.; Liu, X.; Sun, J.; Brongersma, M.; Pop, E.; Cui, Y. Nano Lett. 2015, 15, 6777–6784. doi:10.1021/acs.nanolett.5b02619 |
| 64. | NIST X-ray Photoelectron Spectroscopy (XPS) Database, Version 3.5. https://srdata.nist.gov/xps/Default.aspx (accessed June 27, 2017). |
| 61. | Li, G.; Zhou, H.; Pan, L.; Zhang, Y.; Huang, L.; Xu, W.; Du, S.; Ouyang, M.; Ferrari, A. C.; Gao, H.-J. J. Am. Chem. Soc. 2015, 137, 7099–7103. doi:10.1021/ja5113657 |
| 62. | Whittingham, M. S.; Chianelli, R. R. J. Chem. Educ. 1980, 57, 569. doi:10.1021/ed057p569 |
| 60. | Petrović, M.; Šrut Rakić, I.; Runte, S.; Busse, C.; Sadowski, J. T.; Lazić, P.; Pletikosić, I.; Pan, Z.-H.; Milun, M.; Pervan, P.; Atodiresei, N.; Brako, R.; Šokčević, D.; Valla, T.; Michely, T.; Kralj, M. Nat. Commun. 2013, 4, 2772. doi:10.1038/ncomms3772 |
| 59. | Meng, L.; Wu, R.; Zhou, H.; Li, G.; Zhang, Y.; Li, L.; Wang, Y.; Gao, H.-J. Appl. Phys. Lett. 2012, 100, 083101. doi:10.1063/1.3687688 |
| 60. | Petrović, M.; Šrut Rakić, I.; Runte, S.; Busse, C.; Sadowski, J. T.; Lazić, P.; Pletikosić, I.; Pan, Z.-H.; Milun, M.; Pervan, P.; Atodiresei, N.; Brako, R.; Šokčević, D.; Valla, T.; Michely, T.; Kralj, M. Nat. Commun. 2013, 4, 2772. doi:10.1038/ncomms3772 |
| 61. | Li, G.; Zhou, H.; Pan, L.; Zhang, Y.; Huang, L.; Xu, W.; Du, S.; Ouyang, M.; Ferrari, A. C.; Gao, H.-J. J. Am. Chem. Soc. 2015, 137, 7099–7103. doi:10.1021/ja5113657 |
| 62. | Whittingham, M. S.; Chianelli, R. R. J. Chem. Educ. 1980, 57, 569. doi:10.1021/ed057p569 |
| 63. | Odink, D. A.; Song, K.; Kauzlarich, S. M. Chem. Mater. 1992, 4, 906–911. doi:10.1021/cm00022a029 |
| 56. | Pettenkofer, C.; Jaegermann, W.; Schellenberger, A.; Holub-Krappe, E.; Papageorgopoulos, C. A.; Kamaratos, M.; Papageorgopoulos, A. Solid State Commun. 1992, 84, 921–926. doi:10.1016/0038-1098(92)90459-M |
| 57. | Starnberg, H. I.; Brauer, H. E.; Holleboom, L. J.; Hughes, H. P. Phys. Rev. Lett. 1993, 70, 3111–3114. doi:10.1103/PhysRevLett.70.3111 |
| 58. | Iyikanat, F.; Sahin, H.; Senger, R. T.; Peeters, F. M. APL Mater. 2014, 2, 092801. doi:10.1063/1.4893543 |
| 65. | Dolui, K.; Rungger, I.; Sanvito, S. Phys. Rev. B 2013, 87, 165402. doi:10.1103/PhysRevB.87.165402 |
| 1. | Novoselov, K. S.; Geim, A. K.; Morozov, S. V.; Jiang, D.; Zhang, Y.; Dubonos, S. V.; Grigorieva, I. V.; Firsov, A. A. Science 2004, 306, 666–669. doi:10.1126/science.1102896 |
| 2. | Zhang, Y.; Tan, Y.-W.; Stormer, H. L.; Kim, P. Nature 2005, 438, 201–204. doi:10.1038/nature04235 |
| 3. | Ohta, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Science 2006, 313, 951–954. doi:10.1126/science.1130681 |
| 4. | Castro Neto, A. H.; Guinea, F.; Peres, N. M. R.; Novoselov, K. S.; Geim, A. K. Rev. Mod. Phys. 2009, 81, 109–162. doi:10.1103/RevModPhys.81.109 |
| 5. | Takeda, K.; Shiraishi, K. Phys. Rev. B 1994, 50, 14916–14922. doi:10.1103/PhysRevB.50.14916 |
| 7. | Cahangirov, S.; Topsakal, M.; Aktürk, E.; Şahin, H.; Ciraci, S. Phys. Rev. Lett. 2009, 102, 236804. doi:10.1103/PhysRevLett.102.236804 |
| 22. | De Crescenzi, M.; Berbezier, I.; Scarselli, M.; Castrucci, P.; Abbarchi, M.; Ronda, A.; Jardali, F.; Park, J.; Vach, H. ACS Nano 2016, 10, 11163–11171. doi:10.1021/acsnano.6b06198 |
| 6. | Guzmán-Verri, G. G.; Lew Yan Voon, L. C. Phys. Rev. B 2007, 76, 075131. doi:10.1103/PhysRevB.76.075131 |
| 23. | Mak, K. F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T. F. Phys. Rev. Lett. 2010, 105, 136805. doi:10.1103/PhysRevLett.105.136805 |
| 5. | Takeda, K.; Shiraishi, K. Phys. Rev. B 1994, 50, 14916–14922. doi:10.1103/PhysRevB.50.14916 |
| 19. | Chen, M. X.; Weinert, M. Nano Lett. 2014, 14, 5189–5193. doi:10.1021/nl502107v |
| 5. | Takeda, K.; Shiraishi, K. Phys. Rev. B 1994, 50, 14916–14922. doi:10.1103/PhysRevB.50.14916 |
| 20. | Feng, Y.; Liu, D.; Feng, B.; Liu, X.; Zhao, L.; Xie, Z.; Liu, Y.; Liang, A.; Hu, C.; Hu, Y.; He, S.; Liu, G.; Zhang, J.; Chen, C.; Xu, Z.; Chen, L.; Wu, K.; Liu, Y.-T.; Lin, H.; Huang, Z.-Q.; Hsu, C.-H.; Chuang, F.-C.; Bansil, A.; Zhou, X. J. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 14656–14661. doi:10.1073/pnas.1613434114 |
| 21. | Fleurence, A.; Friedlein, R.; Ozaki, T.; Kawai, H.; Wang, Y.; Yamada-Takamura, Y. Phys. Rev. Lett. 2012, 108, 245501. doi:10.1103/PhysRevLett.108.245501 |
| 13. | Kane, C. L.; Mele, E. J. Phys. Rev. Lett. 2005, 95, 226801. doi:10.1103/PhysRevLett.95.226801 |
| 14. | Lew Yan Voon, L. C. Chin. Phys. B 2015, 24, 087309. doi:10.1088/1674-1056/24/8/087309 |
| 18. | Lin, C.-L.; Arafune, R.; Kawahara, K.; Kanno, M.; Tsukahara, N.; Minamitani, E.; Kim, Y.; Kawai, M.; Takagi, N. Phys. Rev. Lett. 2013, 110, 076801. doi:10.1103/PhysRevLett.110.076801 |
| 8. | Song, Y.-L.; Zhang, S.; Lu, D.-B.; Xu, H.-r.; Wang, Z.; Zhang, Y.; Lu, Z.-W. Eur. Phys. J. B 2013, 86, 488. doi:10.1140/epjb/e2013-31078-4 |
| 9. | Quhe, R.; Fei, R.; Liu, Q.; Zheng, J.; Li, H.; Xu, C.; Ni, Z.; Wang, Y.; Yu, D.; Gao, Z.; Lu, J. Sci. Rep. 2012, 2, 853. doi:10.1038/srep00853 |
| 10. | Ni, Z.; Liu, Q.; Tang, K.; Zheng, J.; Zhou, J.; Qin, R.; Gao, Z.; Yu, D.; Lu, J. Nano Lett. 2012, 12, 113–118. doi:10.1021/nl203065e |
| 11. | Gao, N.; Li, J. C.; Jiang, Q. Phys. Chem. Chem. Phys. 2014, 16, 11673. doi:10.1039/C4CP00089G |
| 12. | Drummond, N. D.; Zólyomi, V.; Fal’ko, V. I. Phys. Rev. B 2012, 85, 075423. doi:10.1103/PhysRevB.85.075423 |
| 17. | Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M. C.; Resta, A.; Ealet, B.; Le Lay, G. Phys. Rev. Lett. 2012, 108, 155501. doi:10.1103/PhysRevLett.108.155501 |
| 6. | Guzmán-Verri, G. G.; Lew Yan Voon, L. C. Phys. Rev. B 2007, 76, 075131. doi:10.1103/PhysRevB.76.075131 |
| 7. | Cahangirov, S.; Topsakal, M.; Aktürk, E.; Şahin, H.; Ciraci, S. Phys. Rev. Lett. 2009, 102, 236804. doi:10.1103/PhysRevLett.102.236804 |
| 15. | Lalmi, B.; Oughaddou, H.; Enriquez, H.; Kara, A.; Vizzini, S.; Ealet, B.; Aufray, B. Appl. Phys. Lett. 2010, 97, 223109. doi:10.1063/1.3524215 |
| 16. | Jamgotchian, H.; Colignon, Y.; Hamzaoui, N.; Ealet, B.; Hoarau, J. Y.; Aufray, B.; Bibérian, J. P. J. Phys.: Condens. Matter 2012, 24, 172001. doi:10.1088/0953-8984/24/17/172001 |
| 17. | Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M. C.; Resta, A.; Ealet, B.; Le Lay, G. Phys. Rev. Lett. 2012, 108, 155501. doi:10.1103/PhysRevLett.108.155501 |
| 30. | Chiappe, D.; Scalise, E.; Cinquanta, E.; Grazianetti, C.; van den Broek, B.; Fanciulli, M.; Houssa, M.; Molle, A. Adv. Mater. 2014, 26, 2096–2101. doi:10.1002/adma.201304783 |
| 24. | Li, L.; Lu, S.; Pan, J.; Qin, Z.; Wang, Y.; Wang, Y.; Cao, G.; Du, S.; Gao, H.-J. Adv. Mater. 2014, 26, 4820–4824. doi:10.1002/adma.201400909 |
| 25. | Dávila, M. E.; Xian, L.; Cahangirov, S.; Rubio, A.; Le Lay, G. New J. Phys. 2014, 16, 095002. doi:10.1088/1367-2630/16/9/095002 |
| 26. | Bampoulis, P.; Zhang, L.; Safaei, A.; van Gastel, R.; Poelsema, B.; Zandvliet, H. J. W. J. Phys.: Condens. Matter 2014, 26, 442001. doi:10.1088/0953-8984/26/44/442001 |
| 27. | Zhang, L.; Bampoulis, P.; van Houselt, A.; Zandvliet, H. J. W. Appl. Phys. Lett. 2015, 107, 111605. doi:10.1063/1.4931102 |
| 28. | Acun, A.; Zhang, L.; Bampoulis, P.; Farmanbar, M.; van Houselt, A.; Rudenko, A. N.; Lingenfelder, M.; Brocks, G.; BPoelsema, K.; atsnelson, M. I.; Zandvliet, H. J. W. J. Phys.: Condens. Matter 2015, 27, 443002. doi:10.1088/0953-8984/27/44/443002 |
| 29. | Zhang, L.; Bampoulis, P.; Rudenko, A. N.; Yao, Q.; van Houselt, A.; Poelsema, B.; Katsnelson, M. I.; Zandvliet, H. J. W. Phys. Rev. Lett. 2016, 116, 256804. doi:10.1103/PhysRevLett.116.256804 |
| 37. | Kresse, G.; Joubert, D. Phys. Rev. B 1999, 59, 1758–1775. doi:10.1103/PhysRevB.59.1758 |
| 38. | Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys. Rev. Lett. 1996, 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865 |
| 34. | Briggs, D.; Seah, M. P. Practical Surface Analysis by Auger and X-Ray Photoelectron Spectroscopy; John Wiley & Sons Ltd: New York, NY, U.S.A., 1983. |
| 35. | Kresse, G.; Furthmüller, J. Phys. Rev. B 1996, 54, 11169–11186. doi:10.1103/PhysRevB.54.11169 |
| 36. | Blöchl, P. E. Phys. Rev. B 1994, 50, 17953–17979. doi:10.1103/PhysRevB.50.17953 |
| 33. | Yu, X.-R.; Liu, F.; Wang, Z.-Y.; Chen, Y. J. Electron Spectrosc. Relat. Phenom. 1990, 50, 159–166. doi:10.1016/0368-2048(90)87059-W |
| 30. | Chiappe, D.; Scalise, E.; Cinquanta, E.; Grazianetti, C.; van den Broek, B.; Fanciulli, M.; Houssa, M.; Molle, A. Adv. Mater. 2014, 26, 2096–2101. doi:10.1002/adma.201304783 |
| 31. | Molle, A.; Lamperti, A.; Rotta, D.; Fanciulli, M.; Cinquanta, E.; Grazianetti, C. Adv. Mater. Interfaces 2016, 3, 1500619. doi:10.1002/admi.201500619 |
| 32. | Wagner, C. D.; Taylor, J. A. J. Electron Spectrosc. Relat. Phenom. 1982, 28, 211–217. doi:10.1016/0368-2048(82)85044-5 |
© 2017 van Bremen et al.; licensee Beilstein-Institut.
This is an Open Access article under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The license is subject to the Beilstein Journal of Nanotechnology terms and conditions: (http://www.beilstein-journals.org/bjnano)